The two bases of a trapezoid measure 14 inches and 10 inches respectively. The trapezoid's height is 8 inches. What is the area of the trapezoid?
Answers
Answer:
A.O.T=1/2×height(sum of bases)
Step-by-step explanation:
A.O.T=1/2×8(14+10)
=4(24)
= 96
Answer:
96
Step-by-step explanation:
Related Questions
What is 98 in exponential form
Answers
We can express the number 98 in exponential form as 10 raised to the power of 2. This means that by multiplying the base, which is 10, by itself twice, we obtain the value of 98.
To express 98 in exponential form, we need to determine the base and exponent that can represent the number 98.
Exponential form represents a number as a base raised to an exponent. Let's find the base and exponent for 98:
We can express 98 as 10 raised to a certain power since the base 10 is commonly used in exponential notation.
To find the exponent, we need to determine how many times we can divide 98 by 10 until we reach 1. This will give us the power to which 10 needs to be raised.
98 ÷ 10 = 9.8
Since 9.8 is still greater than 1, we need to continue dividing by 10.
9.8 ÷ 10 = 0.98
Now, we have reached a value less than 1, so we stop dividing.
From these calculations, we can see that 98 can be expressed as 10 raised to the power of 1 plus the number of times we divided by 10:
98 =\(10^1\) + 2
Therefore, we can write 98 in exponential form as:
98 = \(10^3\)
In summary, 98 can be expressed in exponential form as 10^2. The base is 10, and the exponent is 2, indicating that we multiply 10 by itself two times to obtain 98.
For more such information on: exponential form
https://brainly.com/question/30166689
#SPJ8
3 6 9 12 15 18 21 24 27 30 is odd or even numbers?
Answers
Answer: Half of them are even and half of them are odd.
Step-by-step explanation:
The even numbers are 6, 12, 18, 24, and 30. An even number is defined as a number that is divisible by 2, meaning it has no remainder when divided by 2. For example, 6 divided by 2 equals 3 with no remainder, so 6 is even.
The odd numbers are 3, 9, 15, 21, and 27. An odd number is defined as a number that is not divisible by 2, meaning it has a remainder of 1 when divided by 2. For example, 9 divided by 2 equals 4 with a remainder of 1, so 9 is odd.
Therefore, out of the given numbers, half of them are even and half of them are odd.
________________________________________________________
4 Find the ordered pairs that satisfy the relation y = 6 - x when the domain is {3, 6, 0, -5):
Answers
Answer:
y=0 and x=6 according to questions
Answer:
Step-by-step explanation:
Domain is values on x-axis
y= 6-3=3 (when x=3)
y= 6-6=0 (when x=6)
y= 6-0=6 (when x=0)
y= 6-(-5)= 6 + 5 = 11 (when x= -5)
I need help with this

Answers
The option that can be used to verify the trigonometric identity, \(tan\left(\dfrac{x}{2}\right)+cot\left(x \right) = csc\left(x \right)\) is option C;
C. \(tan\left(\dfrac{x}{2} \right) + cot\left(x \right) = \dfrac{1-cos\left(x \right)}{sin\left( x \right)} +\dfrac{cos \left(x \right)}{sin\left(x \right)} =csc\left(x \right)\)
What is a trigonometric identity?A trigonometric identity is an equations that consists of trigonometric functions that remain true for all values of the argument of the functions
The specified identity is presented as follows;
\(tan\left(\dfrac{x}{2} \right)+cot(x)=csc(x)\)
The half angle formula for tangent indicates that we get;
\(tan\left(\dfrac{1}{2} \cdot \left(\eta \pm \theta \right) \right) = \dfrac{tan\left(\dfrac{1}{2} \cdot \eta \right)\pm tan\left(\dfrac{1}{2} \cdot \theta \right)}{1 \mp tan\left(\dfrac{1}{2} \cdot \eta \right)\times tan\left(\dfrac{1}{2} \cdot \theta \right)}\)
\(\dfrac{tan\left(\dfrac{1}{2} \cdot \eta \right)\pm tan\left(\dfrac{1}{2} \cdot \theta \right)}{1 \mp tan\left(\dfrac{1}{2} \cdot \eta \right)\times tan\left(\dfrac{1}{2} \cdot \theta \right)}=\dfrac{sin \left(\eta\right) \pm sin\left(\theta \right)}{cos \left(\eta \right) + cos \left(\theta \right)} = -\dfrac{cos \left(\eta\right) - cos\left(\theta \right)}{sin \left(\eta \right) \mp sin \left(\theta \right)}\)
When η = 0, we get;
\(-\dfrac{cos \left(0\right) - cos\left(\theta \right)}{sin \left(0 \right) \mp sin \left(\theta \right)}=-\dfrac{1 - cos\left(\theta \right)}{0 \mp sin \left(\theta \right)}=\dfrac{1 - cos\left(\theta \right)}{sin \left(\theta \right)}\)
Therefore;
\(tan\left(\dfrac{x}{2} \right)=\dfrac{1 - cos\left(x \right)}{sin \left(x \right)}\)
\(cot\left(x \right) = \dfrac{cos(x)}{sin(x)}\)
\(tan\left(\dfrac{x}{2} \right)+cot(x)= \dfrac{1 - cos\left(x \right)}{sin \left(x \right)} +\dfrac{cos(x)}{sin(x)}\)
\(\dfrac{1 - cos\left(x \right)}{sin \left(x \right)} +\dfrac{cos(x)}{sin(x)}=\dfrac{1-cos(x)+cos(x)}{sin(x)} = \dfrac{1}{sin(x)}\)
\(\dfrac{1 - cos\left(x \right)}{sin \left(x \right)} +\dfrac{cos(x)}{sin(x)}=\dfrac{1}{sin(x)}=csc(x)\)
Therefore;
\(tan\left(\dfrac{x}{2} \right)+cot(x)= \dfrac{1 - cos\left(x \right)}{sin \left(x \right)} +\dfrac{cos(x)}{sin(x)} = csc(x)\)
The correct option that can be used to verify the identity is option C
Learn more about trigonometric identities in mathematics here:
https://brainly.com/question/14421002
#SPJ1
Find the coordinates of point) along the directed segment AB that partitions it so that the ratio of AP to PB is 1:2. NO LINKS OR ASSESSMENT!!!!

Answers
Answer: (1, 3)
Step-by-step explanation:
There are two ways to solve this problem, 1 without the pythagorean theorem, and 1 with it. For the sake of simplicity, I will solve it without the pythagorean theorem.
As is visually evident from the graph, the line segment spans 6 units horizontally, and 3 units vertically. Because the ratio between AP and PB is 1:2, simply divide both the domain and range by 3, to get 2 horizontally, and 1 vertically.
Then, simply go to point A and respectively add and subtract the horizontal and vertical values to get point A(-1, 4) --> P(1,3)
Hope it helps, and let me know if you want me to solve it an alternate way or go more in depth as to the way it is know.
Answer:
P(1, 3)Step-by-step explanation:
Coordinates of A and B:
A(-1, 4), B(5, 1)The partition ratio:
AP/PB = 1/2Coordinates of P are:
x = -1 + 1/3(5 - (-1)) = -1 + 6/3 = 1y = 4 + 1/3(1 - 4) = 4 - 3/3 = 3100 pts !!!!!! and branlyist (^///^)
Wates 999+34?
Answers
Answer:
Step-by-step explanation:
1033
Answer:
999 + 34 is 1033
Step-by-step explanation:
9 +4 = 13
90+ 30 = 120
900 + 120 + 13 = 1033
Martin wants to buy a new bedroom set that cost $1590 including tax. Unfortunately he doesn’t have $1590 so he secures a 2 year loan from the furniture store at 9% interest to be repaid in 254 equal monthly installments. Find the monthly payment
Answers
The monthly Payment of a 2-year loan of $1590 with 9% interest that needs to be repaid in 254 equal monthly installments is approximately $11.92.
The monthly payment of a 2-year loan of $1590 with 9% interest which needs to be repaid in 254 equal monthly installments, we need to use the loan repayment formula. The formula is given as:
Monthly Payment = (Loan Amount x Monthly Interest Rate) / (1 - (1 + Monthly Interest Rate)^(-Number of Months))
Here,
Loan Amount = $1590
Interest Rate = 9% per annum
Time = 2 years = 24 months
number of Months = 254 (as there are 254 monthly installments)
First, we need to calculate the Monthly Interest Rate using the following formula:
Monthly Interest Rate = Annual Interest Rate / 12
The Annual Interest Rate is 9%,
so the Monthly Interest Rate is: Monthly Interest Rate = 9 / 12 = 0.75%Putting the given values into the loan repayment formula,
we get: Monthly Payment = (1590 x 0.0075) / (1 - (1 + 0.0075)^(-254))= 11.92 (approx)
Therefore, the monthly payment of a 2-year loan of $1590 with 9% interest that needs to be repaid in 254 equal monthly installments is approximately $11.92.
For more questions on Payment .
https://brainly.com/question/25792915
#SPJ8
Part IV Questions: Answer all the questions in this part. Each problem isworth 6 points.Exercise #5:The steps to simplifying the product: 5x • 2x? The simplest terms areshown below. Write in what justifies each step.Step 1: 5x3 • 2x? = 5 • 2•x.x?Justification:Step 2: 5•2•x •x? = (5 • 2) : (x} . x) Justify:Step 3: (5.2) (x3 • x?) = 10x10Justify

Answers
We are given the following expression
\(5x^3\cdot2x^7\)We are asked to provide justification on how it is being simplified.
Step 1: Justification
Since the base is the same (x) the coefficients are multiplied together.
\(mx^a\cdot nx^b=m\cdot n\cdot x^a\cdot x^b\)Step 2: Justification
Combining the like terms together
\(m\cdot n\cdot x^a\cdot x^b=(m\cdot n)\cdot(x^a\cdot x^b)\)Step 3: Justification
Apply the exponent's rule (since the base is the same their powers can be added)
\(x^a\cdot x^b=x^{a+b}\)Multiples that are shared by two or more numbers are____
Answers
Answer:
Multiples that are shared by two or more numbers are common multiples.
Step-by-step explanation:
A common multiple is a whole number that is a shared multiple of each set of numbers. The multiples that are common to two or more numbers are referred to as the common multiples of those numbers.
I hope this helps! ^-^
Jocelyn has a ladder that is 15 ft long. She wants to lean the ladder against a vertical wall so that the top of the ladder is 13.5 ft above the ground. For safety reasons, she wants the angle the ladder makes with the ground to be less than 75°. Will the ladder be safe at this height? Show your work and equation to support your answer
Answers
By using trigonometric relations, we will see that the angle that the ladder makes with the ground is 64.2°, so we conclude that the ladder is safe.
Will the ladder be safe at this height?Notice that the ladder makes a right triangle with the wall.
Such that the hypotenuse (the ladder itself) measures 15 ft, and one of the catheti (distance between the ground and top of the ladder) measures 13.5ft
If we considerate the angle that the ladder makes with the ground, the known cathetus is the opposite cathetus.
Then we can use the relation:
sin(x) = (opposite cathetus)/(hypotenuse)
Then:
sin(x) = (13.5ft)/(15ft)
If we use the inverse sine function on both sides, we get:
Asin(sin(x)) = Asin( 13.5ft/15ft)
x = Asin(13.5/15) = 64.2°
So the angle is less than 75°, which means that in fact, the ladder is safe.
If you want to learn more about right triangles:
https://brainly.com/question/2217700
#SPJ1
find the indicated limit if it exists

Answers
Answer:
\(\displaystyle \lim_{x \to \infty} \frac{x^2}{1 + 3x + 5x^2} = \frac{1}{5}\)
General Formulas and Concepts:
Calculus
LimitsStep-by-step explanation:
Step 1: Define
\(\displaystyle \lim_{x \to \infty} \frac{x^2}{1 + 3x + 5x^2}\)
Step 2: Determine Rule
If the highest power of x in a rational expression is the same both numerator and denominator, then the limit as x approached ∞ would be the highest term coefficient in the numerator divided by the highest term coefficient in the denominator.
Step 3: Identify
Numerator highest power: x²
Coefficient: 1Denominator highest power: 5x²
Coefficient: 5Step 4: Evaluate
Apply rule.
\(\displaystyle \lim_{x \to \infty} \frac{x^2}{1 + 3x + 5x^2} = \frac{1}{5}\)
Topic: AP Calculus AB/BC (Calculus I/II)
Unit: Limits
Book: College Calculus 10e
g(x) = 2x + 1h(x) = x + 2xFind (g + h)(x)
Answers
g(x) = 2x + 1
h(x) = x + 2x
(g + h)(x) = (2x + 1) + (x + 2x)
(g + h) (x) = 2x + 1 + x + 2x
(g + h) (x) = 2x + 2x + x + 1
(g + h)(x) = 5x + 1 Result
How would you do this type of problem and what would the increasing and decreasing interval be
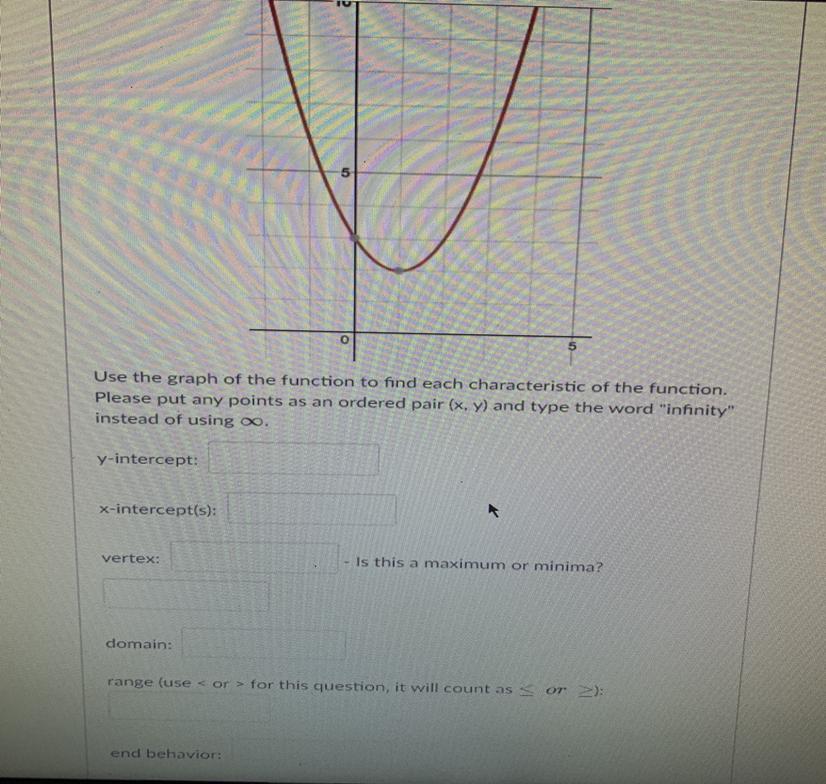
Answers
y-intercept is the point in the y-axis that the graph intersects.
From the figure, the graph intersects at point (0, 3)
The y- intercept is (0, 3)
x-intercept is the point in the x-axis that the graph intersects.
Since the graph does not intersects the x-axis, the x-intercept does not exist
Vertex is a point on the graph that is a maximum or a minimum.
The vertex of the graph which is the lowest point as shown in the figure is at point (1, 2)
And this is a minima, since it is the lowest point.
Domain is the set of x-values that exist in the graph, the graph is going infinitely to the left and to the right, therefore the domain is (-∞, ∞)
Range is the set of y-values that exist in the graph, the y values starts from the vertex which is the lowest point at (1, 2) going upward.
So the range is all real numbers greater than or equal to 2. [2, ∞)
End behavior is the behavior of the function at large positive and negative values of x.
when x goes positive infinity, f(x) goes to positive infinity
As x ⇒ ∞, f(x) ⇒ ∞
when x goes negative infinity, f(x) goes to negative infinity
As x ⇒ -∞, f(x) ⇒ -∞
Decreasing interval occurs when the graph is going down, and increasing interval occurs when the graph is going up.
Decreasing interval will be (-∞, 1]
Increasing interval will be [1, ∞)
PLS HELP WITH THIS one

Answers
Since the 4 is a coefficient you cannot subtract it from the 4 on the other side of the equal sign therefor the only number left is 12. Since you do opposite property’s it’s subtraction. Hope this helps
A straw is placed inside a rectangular box that is 3 inches by 7 inches by 6 inches, as shown. If the straw fits exactly into the box diagonally from the bottom left corner to the top right back corner, how long is the straw? Leave your answer in simplest radical form.
Answers
Answer:
3sqrt(5)
Step-by-step explanation:
We can use the Pythagorean theorem to find the length of the diagonal of the rectangular box.
The Pythagorean theorem states that for a right triangle with legs of length a and b and hypotenuse of length c, we have:
c^2 = a^2 + b^2
In this case, the legs of the right triangle are 3 inches and 6 inches, and the hypotenuse is the length of the straw. So we have:
straw length^2 = 3^2 + 6^2 straw length^2 = 9 + 36 straw length^2 = 45
Taking the square root of both sides, we get:
straw length = sqrt(45) = sqrt(9*5) = sqrt(9)*sqrt(5) = 3sqrt(5)
Therefore, the length of the straw is 3sqrt(5) inches.
A car travels 60 kilometers in one hour before a piston breaks, then travels at 30 kilometers per hour for the remaining 60 kilometers to its destination. What is its average speed in kilometers per hour for the entire trip?
Answers
Answer:
Total Distance : 1*60 +60=120
Total time taken = 1+ 60/30= 1+2=3
Hence average speed for the trip = 120/3= 40 kmph
Hence Answer is 40
Step-by-step explanation:
The average speed is 40 km/h.
What is Average speed?The average speed of a body is equal to the total distance covered, divided by the total time taken. The formula for average speed is given as:
Average Speed Formula:Average Speed = Total distance covered ÷ Total time taken
Example:
sing the average speed formula, find the average speed of Sam, who covers the first 200 kilometers in 4 hours and the next 160 kilometers in another 4 hours.
Solution:
To find the average speed we need the total distance and the total time.
Total distance covered by Sam = 200Km + 160 km = 360 km
Total time taken by Sam = 4 hour + 4 hour = 8 hour
Average Speed = Total distance covered ÷ Total time taken
Average Speed = 360 ÷ 8 = 45km/hr
Given:
d1= 60 km
d2= 30
d3 = 60
Total Distance : 1*60 +60=120
Total time taken = 1+ 60/30= 1+2=3
Now,
average speed = total distance/ total time taken
= 120/3
= 40 kmph
Learn more about average speed here;
https://brainly.com/question/12322912
#SPJ2
I need answer ASAP plz hurry

Answers
Calculate the surface area

Answers
To calculate the surface area of a rectangular prism, we need to find the area of each of its six faces and then add them up. In this case, the dimensions of the shape are:
Length = 8 cmWidth = 3 cmHeight = 6 cmRefer to the attachment below.
Three pairs of facesThere are three pairs of faces on a rectangular prism:
Two faces (top & bottom) with dimensions: Length × Width (8 cm × 3 cm).Two faces (front & back) with dimensions: Length × Height (8 cm × 6 cm).Two faces (left & right) with dimensions: Width × Height (3 cm × 6 cm).Finding the areaArea of Length × Width faces8 cm × 3 cm = 24 cm²
Since there are two of these faces, the total area is:
2 × 24 = 48 cm²
Area of Length × Height faces8 cm × 6 cm = 48 cm²
Since there are two of these faces, the total area is:
2 × 48 = 96 cm²
Area of Width × Height faces3 cm × 6 cm = 18 cm²
Since there are two of these faces, the total area is:
2 × 18 = 36 cm²
Adding the areas of the facesNow, add up the areas of all six faces:
Surface Area = 48 + 96 + 36 = 180 cm²
AnswerSo, the surface area of the rectangular prism is 180 cm².
________________________________________________________
Learn MoreTo learn more about the surface area of shapes, refer to:
https://brainly.com/question/31978573
https://brainly.com/question/32198861
https://brainly.com/question/26883871
https://brainly.com/question/30816589
https://brainly.com/question/27847638
https://brainly.com/question/15476432
https://brainly.com/question/14001755
https://brainly.com/question/29298005

What does 10.98+4.06
Answers
Answer:
15.01
Step-by-step explanation:
10.95+4.06
Answer:
15.01
Hope that helps :-)
Which choice correctly expresses the number below in scientific notation?
5,790,000
A) 5.79 • 10^7
B) 579 • 10^4
C) 57.9 • 10^5
D) 5.79 • 10^6
E) 579 • 10^6
F) 5.79 • 10^5
Answers
Answer:
D
Step-by-step explanation:
In scientific notation, the number that is being multiplied by the power of ten must be greater than or equal to 1 and less than 10. This eliminates options B, C, and E. The rest of the options are all 5.79 times something. To find that something, we can do 5,790,000 / 5.79 = 1000000 = 10⁶. This means that the answer is D.
the height y (in feet) of a ball thrown by a child
Y=-1/16x^2+4x+3
Answers
Using Quadratic formula, x = 0.18 ft.
Keep in mind that since the quadratic is downward facing, the vertex will be the highest point, the y-intercept will represent the starting height, and the positive x-intercept will represent the distance to the child.
(a) Locate the y-intercept by setting x = 0 and solving for y.
y = -116(0)2+4(0)+3 = 3 ft
(b) As the maximum height is being requested, determine the vertex's y-value.
Vertex x-value: x=-b/2a=-4/(2*-116)=1/58
Vertex's y-value is given by: y = -116(1/58)2+4(1/58)+3 = 3.03 ft (return the x-value to the equation).
Locate the positive x-intercept (y = 0) in (c).
0 = -116x2+4x+3
Using the quadratic formula because it cannot be factored
x = [-4 ± √(42-4(-116)(3))]
/(2*-116) = -0.14 or 0.18 ft
x = 0.18 ft
To learn more about quadratic formula from given link
https://brainly.com/question/1214333
#SPJ1
Complete Question -
The height y (in feet) of a ball thrown by a child is y=−116x2+4x+3
The height y (in feet) of a ball thrown by a child is
y=−116x2+4x+3
where x is the horizontal distance in feet from the point at which the ball is thrown.
(a) How high is the ball when it leaves the child's hand? feet
(b) What is the maximum height of the ball? feet
(c) How far from the child does the ball strike the ground? Round your answers to the nearest 0.01. feet
(SOMEBODY PLEASE HELP ME!!- ILL GIVE BRAINLIEST AND THERE IS 10 POINTS- PLEASE HELP-)
There are two numbers. The sum of the larger number and three times the smaller number is 14. The larger number is two more than the
smaller number.
What is the larger number?
OA. 2
OB. 3
C. 4
ODS

Answers
Answer:
Step-by-step explanation:
The larger number is four I think
Answer:
5
Step-by-step explanation:
14-2 = 12
12÷4=3 (smaller number)
3+2=5
a, b, c, and d are four different numbers and the proportion is true, which of the following is false?
Answers
If a, b, c, and d are four different numbers and the proportion a/b = c/d is true, then none of the statements is false.
What is proportion?
In general, the term "proportion" refers to a part, share, or amount that is compared to a whole. According to the definition of proportion, two ratios are in proportion when they are equal.
Since a/b = c/d, are proportional then can cross-multiply to get ad = bc.
Now, evaluate each statement -
A. b/a = d/c
Cross-multiplying, it is obtained that bc = ad, which is true based on the original proportion.
Therefore, this statement is true.
B. a/c = b/d
Cross-multiplying, it is obtained ad = bc, which is also true based on the original proportion.
Therefore, this statement is true.
C. b/a = c/d
This is equivalent to the original proportion, so it is true.
D. (a + b)/b = (c + d)/d
Simplify the equation -
d(a + b) = b(c + d)
da + db = bc + bd
da = bc
Cross-multiplying, it is obtained that da = bc, which is true based on the original proportion.
Therefore, this statement is true.
To learn more about proportion from the given link
https://brainly.com/question/19994681
#SPJ1

How can you check if a line belongs to a plane (Cartesian equation of the line and the equation of the plane is given)?
Answers
For example, suppose you have the Cartesian equation of a line in the form:
y = mx + b
and the equation of a plane in the form:
ax + by + cz + d = 0
To check if the line belongs to the plane, you can substitute a point (x, y) on the line into the equation of the plane and solve for z. If the resulting value of z satisfies the equation of the plane, then the line belongs to the plane.
Here's an example:
Suppose the Cartesian equation of the line is y = 2x + 1, and the equation of the plane is 2x + 3y + 4z + 5 = 0.
If we substitute a point on the line, such as (1, 3), into the equation of the plane, we get:
2(1) + 3(3) + 4z + 5 = 0
Solving for z, we find that z = -1.5.
Since the resulting value of z satisfies the equation of the plane, the line belongs to the plane.
If the resulting value of z does not satisfy the equation of the plane, then the line does not belong to the plane.
What percentage of students attend either public school or college
Answers
The percentage of students attend either public school or college will be 90%.
How to illustrate the percentage?Let the students in public school be 40%
Let the students in college be 50%
Let those who stay at home be 10%
Therefore, the percentage of students attend either public school or college will be:
= 40% + 50%
= 90%
Therefore, the percentage of students attend either public school or college will be 90%.
Learn more about percentages on:
brainly.com/question/24304697
#SPJ1
In a school, the following information are given:
Public school students = 40
Number of those in college = 50
Number of those at home = 10
What percentage of students attend either public school or college?
a. 90%
b. 50%
c. 40%
d. 10%
Caroline went to the grocery store and bought bottles of soda and bottles of juice.
Each bottle of soda has 30 grams of sugar and each bottle of juice has 15 grams of sugar. Caroline purchased a total of 6 bottles of juice and soda which collectively contain 150 grams of sugar. Graphically solve a system of equations in order to determine the number of bottles of soda purchased, ∞, and the number of bottles of juice purchased, y.
Answers
The solution of the system of equations is the point of intersection (4, 2), as shown in the graph below.
Caroline bought 4 soda bottles.
Caroline bought 2 juice bottles.
How to Solve a System of Equations?In order to determine the solution to this problem, use the information given to create two equations.
Number of soda bottle = x.
Number of juice bottle = y.
First Equation for the total number of bottle that Kelvin bought
x + y = 6 --> eqn. 1
Second Equation 2 for the total sugar in the soda bottles and total sugar in juice bottles that equals 150 grams of sugar.
30x + 15y = 150
Simplify by dividing by 5
6x + 3y = 30 --> eqn. 2
Rewrite eqn. 1:
y = 6 - x
Solve simultaneously for the variables of x and y, by substituting the value of y into equation 2:
6x + 3(6 - x) = 30
6x + 18 - 3x = 30
3x + 18 = 30
3x = 30 - 18
3x = 12
3x/3 = 12/3
x = 4
Caroline bought 4 soda bottles.
Substitute x = 4 into equation 1 to find the value of y:
x + y = 6
4 + y = 6
y = 6 - 4
y = 2
Caroline bought 2 juice bottles.
The graph below shows the point of intersection, (4, 2), which is the solution.
Learn more about the system of equations on:
https://brainly.com/question/25869125
#SPJ1

2. How many radians are in 27"?
Answers
The answer is 0.471 radians.
FORMULA:
Just do 27° × π/180 = 0.4712rad but then cut off the two.
In each expression below, identify the coefficient, constant, and variable. a. 7 + 9 b. 6 – 5 c. 4.5 – 2.7
Answers
The variable is the letter like x or y. The coefficient is the number next to the variable like the 2 in 2x or if its just x it would be 1. The constant is the number by itself usually at the end.
Example 2x+5
Variable is x constant is 5 and coefficient is 2. Sorry i didn't answer the actual question and just told you how to find it but those expressions don't have any of these things.
Answer:
-1 and 1/3
Step-by-step explanation:
I replaced each variable with 1. Other than that I just guessed and got it right lol

What is the Voter Registration Act and how does it affect Gerrymandering?
Answers
Answer:
United States federal law signed into law by President Bill Clinton on May 20, 1993, and which came into effect on January 1, 1995.
Step-by-step explanation:
Hope It Helps :)
in a classroom for every eight girls there are five boys what is the ratio of boys to girls?
Answers
Answer:
5:8
Step-by-step explanation: