The triangle above has the following measures
m/C=45 degrees
a=7.5 yd
Use the 45-45-90 Trangle Theorem to find the
length of the hypotenuse Include correct units.
Show all your work.

Answers
The length of the hypotenuse is given as follows:
b = 10.6 yd.
What is the Pythagorean Theorem?The Pythagorean Theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the longest side) is equal to the sum of the squares of the lengths of the other two sides.
The theorem is expressed as follows:
c² = a² + b².
In which:
c is the length of the hypotenuse.a and b are the lengths of the other two sides (the legs) of the right-angled triangle.By the 45-45-90 Triangle Theorem, the two sides have the same length, hence:
a = c = 7.5.
Hence the hypotenuse b is obtained as follows:
b² = a² + c²
b² = 7.5² + 7.5²
\(b = \sqrt{7.5^2 + 7.5^2}\)
b = 10.6 yd.
More can be learned about the Pythagorean Theorem at brainly.com/question/30203256
#SPJ1
Related Questions
1/6y + 3/6y = 10
Hurry plaz
Answers
Y=15
1. use standard form
2/3y _ 10 = 0
2. Factorization
2/3 (y _ 15) =0
3. solution
y = 60/4
y = 15
PLEASE HELP!
Fill in the blank
1. 40 times the sum of 24 and 36
2. Divide the difference between 1,600 and 400 by 4

Answers
Answer:
A. The expression of "40 times the sum of 24 and 36" would be 40 x (24+36), and the value would be 2400.
B. for the words portion it would be "20 times the sum of 650 and 350", and the value of that expression is 20,000.
C. The expression of "divide the difference between 1,600 and 400 by 4" should be 1200 / 4, and if that is the correct way to format the expression then the value would be 300.
D. for the words portion it would be "100 times the sum of 78 and 12", and the value of that expression is 10,000.
Step-by-step explanation:
Answer:
40 times the sum of 24 and 36
40 × (24 + 36)
2400
20 times the sum of 650 and 350
20000
divide the difference between 1600 and 400 by 4
(1600 - 400) ÷ 4
300
100 times the sum of 78 and 12
9000
which set of points does not determine a spherical triangle?
Answers
Therefore, the set of points that does not determine a spherical triangle is any set of three non-collinear points that do not lie on a great circle of the sphere.
Explanation: A spherical triangle is a triangle formed on the surface of a sphere by three great circle arcs intersecting pairwise to form three vertices. Any three points that do not lie on a great circle of the sphere will not determine a spherical triangle. Therefore, the set of points that does not determine a spherical triangle is any set of three non-collinear points that do not lie on a great circle of the sphere. Any set of three non-collinear points that do not lie on a great circle of the sphere does not determine a spherical triangle.
Therefore, the set of points that does not determine a spherical triangle is any set of three non-collinear points that do not lie on a great circle of the sphere.
To know more about triangle visit:
https://brainly.com/question/1058720
#SPJ11
you are going to create a caramel cheese popcorn mixture. one cup of caramel popcorn contains 183 calories, 5.4 grams fat, 22.5 grams sugar, and 87 mg of sodium. one cup of cheese popcorn contains 58 calories, 3.7 grams fat, 0.1 grams sugar, and 98 mg sodium. if you create a mixture that has two times as much cheese popcorn as caramel popcorn and contains a total of 254 calories, how many cups of each item would be in your mixture. be sure to clearly define the variables used, define the two equations, and show and explain all work.
Answers
The mixture would contain approximately 0.849 cups of caramel popcorn and 1.698 cups of cheese popcorn.
Let's define the variables:
Let x be the number of cups of caramel popcorn in the mixture
Let y be the number of cups of cheese popcorn in the mixture
We are given that the mixture has two times as much cheese popcorn as caramel popcorn, so y = 2x.
We are also given that the total number of calories in the mixture is 254. To find an equation that relates x and y, we can use the calorie information for each type of popcorn:
Calories from caramel popcorn = 183x
Calories from cheese popcorn = 58y = 58(2x) = 116x
Total calories in the mixture = 183x + 116x = 299x
Setting the total calories equal to 254 and solving for x:
299x = 254
x = 0.849
So we would need 0.849 cups of caramel popcorn in the mixture.
To find the number of cups of cheese popcorn, we can use the equation y = 2x:
y = 2(0.849) = 1.698
So we would need 1.698 cups of cheese popcorn in the mixture.
Therefore, the mixture would contain approximately 0.849 cups of caramel popcorn and 1.698 cups of cheese popcorn.
To learn more about mixture
https://brainly.com/question/13461506
#SPJ11
Please help em fast I really need help
lf ƒ(x) = 2(x + 1)² and g(x) = 3x- 2 determine f[g(2)]
Answers
Answer:
f(g(2)) = 50
Step-by-step explanation:
evaluate g(2) then substitute the result obtained into f(x)
g(2) = 3(2) - 2 = 6 - 2 = 4 , then
f(4) = 2(4 + 1)² = 2(5)² = 2(25) = 50
Answer:
f[g(2)] = 50
Step-by-step explanation:
Given functions:
\(f(x)=2(x+1)^2\)
\(g(x)=3x-2\)
We are asked to determine f[g(2)], which is known as a composite function. When solving composite functions, you always work inside out.
Step 1: Find the value of g(2) by substituting 2 for x in function g(x).
\(\implies g(2)=3(2)-2\)
\(\\\implies g(2)=6-2\Rightarrow g(2)=\boxed{4}\)
Step 2: Substitute the found value into the composite function.
\(\\\implies f[g(2)]= 2(4+1)^2\)
\(\implies f[g(2)] = 2(5)^2 \Rightarrow 2(25) \Rightarrow \boxed{50}\)
Hence, the value of the composite function f[g(2)] is 50.
Learn more about composite functions here:
brainly.com/question/28062427
brainly.com/question/26215408
g(x)=2x+4 solve for c when g(x)-8
Answers
Answer: ( g+G) (x) =12+2x
Step-by-step explanation:
i used an math ap it is an app you can get on your phone
a new concrete drill costs $1,500. if the price of drills has increased by 2% in the past year, how much did the drill cost 1 year ago? assume the price increase follows a9simple interest calculation. group of answer choices $1,250.00 $1,464.84 $1,497.01 $1,470.59
Answers
To find the cost of the drill one year ago, we can use the concept of simple interest.
Let's denote the cost of the drill one year ago as "P". The price of the drill currently is $1,500, and it has increased by 2% over the past year. Using the simple interest formula:
Price after 1 year = Principal (1 + Interest Rate)
$1,500 = P (1 + 0.02) To find P, we rearrange the equation:
P = $1,500 / (1 + 0.02)
P ≈ $1,470.59 Therefore, the drill cost approximately $1,470.59 one year ago. The closest option from the given choices is $1,470.59.
To know more about simple interest:- https://brainly.com/question/30964674
#SPJ11
What is the answer to 3+x
Answers
Given the function f(x)=-3(x)^2, find the value of f(5).
Answers
Answer:
75
Step-by-step explanation:
you just put the 5 in the x's spot in the equation
lee built 5 toys in 5 minute. At this rate, how many toys would he build in 9 hours ?
Answers
Answer:
Step-by-step explanation:
If Lee builds 5 toys in 5 minutes, then that means he builds 1 toy per minute
Additionally, in 9 hours, there are 540 minutes (9 * 60)
If Lee creates 1 toy per minute for 540 minutes, he will have 540 toys
If Lee builds 5 toys in 5 minutes, then that means he builds 1 toy per minute
Additionally, in 9 hours, there are 540 minutes (9 * 60)
If Lee creates 1 toy per minute for 540 minutes, he will have 540 toys
Find the area and perimeter of a square that has a side length of 4. Remember area is a length times width and perimeter is when you add all the sides together.
Answers
Answer:
Area= 16
Perimeter= 16
Answer:
A = l*w
P = 2l + 2w
A = 4*4 = 16
A = area
l = length
l = 4
w = width
w = 4
The area is equal to 16.
P = 2*4 + 2*4 = 16
P = perimeter
2l = 2*length
2l = 2*4
2w = 2*width
2w = 2*4
The perimeter is equal to 16.
It can be concluded both are equal to each other.
Hope this helps
5. Determine the Critical points and locate any relative minima, maxima and saddle points of function f defined by : f(x, y) = 2x² + 2xy + 2y² - 6x 6. Determine the Critical points and locate any relative minima, maxima and saddle points of function f defined by : f(x, y) = 2x² - 4xy + y +2 7. Determine the Critical points and locate any relative minima, maxima and saddle points of function f defined by : f(x, y) = -x -y + 4xy
Answers
In calculus, critical points are those points where the function has either maximum, minimum, or saddle values. For determining the critical points, we take the first derivative of the function and equate it to zero. 5. Given, f(x, y) = 2x² + 2xy + 2y² - 6x
We will determine the partial derivatives with respect to x and y first.$$f_x=4x+2y-6$$$$f_y=4y+2x$$
Now, we will equate both to zero and solve for x and y.$$4x+2y-6=0$$$$4y+2x=0$$Solving for x and y, we get the critical point as $(1,1)$.
To determine the nature of critical points, we calculate the determinant of the Hessian matrix. $$H(f(x,y))=\begin{bmatrix} f_{xx}(x,y) & f_{xy}(x,y)\\ f_{yx}(x,y) & f_{yy}(x,y)\\ \end{bmatrix}$$For function 5, $$H(f(x,y))=\begin{bmatrix} 4 & 2\\ 2 & 4\\ \end{bmatrix}$$
Now, the determinant of the Hessian matrix is $$D=4\times4-2\times2=16-4=12$$This value is greater than zero,
which means we have a minimum at the point $(1,1)$.Thus, the critical point is a relative minimum.6. Given, f(x, y) = 2x² - 4xy + y +2First, we will determine the partial derivatives with respect to x and y. $$f_x=4x-4y$$$$f_y=-4x+1$$Now, we will equate both to zero and solve for x and y.$$4x-4y=0$$$$-4x+1=0$$Solving for x and y, we get the critical point as $(\frac{1}{4},\frac{1}{16})$.
For the Hessian matrix of function 6, $$H(f(x,y))=\begin{bmatrix} 4 & -4\\ -4 & 0\\ \end{bmatrix}$$The determinant of this matrix is $D=0-16<0$, so we have a saddle point at the critical point $(\frac{1}{4},\frac{1}{16})$.Thus, the critical point is a saddle point.7. Given, f(x, y) = -x -y + 4xy.
The Hessian matrix for function 7 is $$H(f(x,y))=\begin{bmatrix} 0 & 4\\ 4 & 0\\ \end{bmatrix}$$Thus, the critical point is a saddle point.$Relative minimumf(x, y) = 2x² - 4xy + y +2$(\frac{1}{4},\frac{1}{16})$Saddle pointf(x, y) = -x -y + 4xy$(\frac{1}{4},\frac{1}{4})$Saddle point
To know more about critical points visit:-
https://brainly.com/question/23946365
#SPJ11
When the declaration/// int y = 5; /// is followed by the
assignment /// y += 3.7; /// the value of y is _______.
Answers
Answer:
y = 8.7
Step-by-step explanation:
Assuming we can use decimal places, y is equal to 8.7.
In programming, += is often used as a substitute for y = y + x (example)
Therefore, y = y + 3.7, and since y = 5, y = 5 + 3.7, y = 8.7
find the critical t-value for a 95onfidence interval using a t-distribution with 20 degrees of freedom. round your answer to three decimal places, if necessary.
Answers
The critical t-value for a 95% confidence interval with 20 degrees of freedom is approximately 2.093.
In statistical analysis, a confidence interval provides a range of values within which we can expect a population parameter to lie. The critical t-value is used to determine the width of the confidence interval for a given level of confidence and degrees of freedom. In this case, we are looking for the critical t-value for a 95% confidence interval with 20 degrees of freedom.
The t-distribution is a probability distribution that is similar to the normal distribution but accounts for the uncertainty introduced when estimating a population parameter from a sample. The degrees of freedom represent the number of independent pieces of information used to estimate the population parameter.
To find the critical t-value, we consult a t-distribution table or use statistical software. With 20 degrees of freedom and a 95% confidence level, we find the corresponding value to be approximately 2.093. This means that approximately 95% of the t-distribution falls within the range of -2.093 to 2.093, with the remaining 5% lying in the tails.
Learn more about confidence interval
brainly.com/question/32546207
#SPJ11
Carmen is simplifying the expression (6. 21 0. 93) 0. 7. She recognizes that 0. 93 and 0. 07 will combine to equal 1, so she would like to find that sum before she adds 6. 21. Which property will allow Carmen to do this without changing the value of the expression? associative property commutative property distributive property identity property.
Answers
To solve the problem w must know about the Associative property.
Associative propertyThe associative property states that the addition of the sum of two numbers (a,b) and a third number(c) is equal to the addition of the sun of the last two numbers(b, c) and the first number(a).
A+(B+C) = (A+B)+CThe property that will allow Carmen to do this without changing the value of the expression is the Associative property.
ExplanationGiven to us
(6.21 + 0.93 ) + 0.07Associative property.Now, using Associative property,
(6.21 + 0.93 ) + 0.07
= 6.21 + (0.93 + 0.07)
=6.21 + (0.93 + 0.07)
Hence, the property that will allow Carmen to do this without changing the value of the expression is the Associative property.
Learn more about Associative property:
https://brainly.com/question/1680548
Need help with this please and thank you!!!!

Answers
The equation of the graph is y=x+1.
What is Slope of Line?The slope of the line is the ratio of the rise to the run, or rise divided by the run. It describes the steepness of line in the coordinate plane.
The slope intercept form of a line is y=mx+b, where m is slope and b is the y intercept.
The slope of line passing through two points (x₁, y₁) and (x₂, y₂) is
m=y₂-y₁/x₂-x₁
The two points from the graph are (1,2) and (2, 4).
m=2/2=1
We have to find the y intercept.
2=1(1)+b
b=1
The slope intercept form is y=x+1
Hence, the equation of the graph is y=x+1.
To learn more on slope of line click:
https://brainly.com/question/14511992
#SPJ1
Suppose that consumer has the following utility function: U(X,Y)= X¹/2y1/4. Suppose also that Px 2, Py = 3 and I = 144. What would be the optimal consumption of X and Y at the equilibrium, respectively? a) 24, 32 b) 12, 40 c) 48, 16 d) 36, 24
Answers
The 48 units of X and 16 units of Y. The correct answer is option C.
To determine the optimal consumption of goods X and Y for the consumer with the utility function \($U(X,Y) = X^{1/2}Y^{1/4}$\), we need to maximize utility subject to the given prices and income.
Let's denote the quantities of X and Y consumed as $x$ and $y$, respectively. The consumer's problem can be formulated as the following constrained optimization:
\(Maximize} \quad & U(X,Y) = X^{1/2}Y^{1/4} \\Subject to} \quad & Px \cdot x + Py \cdot y = I\)
where Px and Py are the prices of goods X and Y, and I is the consumer's income.
Given Px = 2, Py = 3, and I = 144, we can substitute these values into the constraint equation:
\($$2x + 3y = 144$$\)
To solve this problem, we can use the Lagrange multiplier method. We construct the Lagrangian function:
\($$\mathcal{L}(x, y, \lambda) = X^{1/2}Y^{1/4} - \lambda(2x + 3y - 144)$$\)
Taking partial derivatives and setting them equal to zero:
\(\frac{\partial \mathcal{L}}{\partial x} &= \frac{1}{2}X^{-1/2}Y^{1/4} - 2\lambda = 0 \\\\\frac{\partial \mathcal{L}}{\partial y} &= \frac{1}{4}X^{1/2}Y^{-3/4} - 3\lambda = 0 \\\\\\\frac{\partial \mathcal{L}}{\partial \lambda} &= -(2x + 3y - 144) = 0\)
Simplifying these equations, we obtain:
\(\frac{Y^{1/4}}{2X^{1/2}} &= 2\lambda \\\\\frac{X^{1/2}}{4Y^{3/4}} &= 3\lambda \\\\2x + 3y &= 144\)
By equating the two expressions for $\lambda$, we can eliminate it:
\(\frac{Y^{1/4}}{2X^{1/2}} &= \frac{X^{1/2}}{4Y^{3/4}} \\\\4Y^{7/4} &= 2X \\\\2Y^{7/4} &= X^{1/2} \\\\16Y^{7/2} &= X\)
Substituting this expression for X in the budget constraint:
\($$2(16Y^{7/2}) + 3Y = 144$$\)
Simplifying:
\($$32Y^{7/2} + 3Y = 144$$\)
This equation can be solved numerically, and the solution is \($Y \approx 16.81$\). Substituting this value back into the expression for X:
\($$X \approx 47.35$$\)
Rounding these values to the nearest whole number, the optimal consumption of goods X and Y at the equilibrium is approximately 47 units of X and 17 units of Y.
Therefore, the correct answer is option (c): 48 units of X and 16 units of Y.
To learn more about units from the given link
https://brainly.com/question/18522397
#SPJ4
The coordinates of the vertices of parallelogram CDEH are C(5,5), D(2,5) and H(8,1). What are the coordinates for E?
Answers
The coordinates for E from the parallelogram CDEH are (5, 1).
We know that diagonals of parallelograms bisect each other. Therefore coordinates of the midpoint of CE and DH will be the same.
Here, (x, y) = [(2+8)/2, (5+1)/2]
= (5, 3)
Let the coordinates of E be (a, b)
Now, (5, 3) = [(5+a)/2, (5+b)/2]
(5+a)/2 =5 and (5+b)/2 = 3
5+a=10 and 5+b=6
a=10-5 b=6-5
a=5 b=1
Therefore, the coordinates for E from the parallelogram CDEH are (5, 1).
Learn more about the parallelogram here:
https://brainly.com/question/19187448.
#SPJ1
Use Horner's algorithm to find p(4), where p(z) = 325 – 724 – 57'+z? -- 8z +2 2.
Answers
Using Horner's algorithm, it is found that p(4) = 946.
Horner's algorithm is a method used to evaluate a polynomial at a given value of x. It simplifies the process of calculating the value of the polynomial by reducing the number of calculations needed. To use Horner's algorithm to find p(4), where p(z) = 3z^5 – 7z^4 – 5z^3+z^2- 8z +2, follow these steps:
p(4) = 3(4)^5 – 7(4)^4 – 5(4)^3+(4)^2- 8(4) +2
p(4) = 3(4)^5 – 7(4)^4 – 5(4)^3+(4)^2- 8(4) +2
p(4) = 3(1024) – 7(256)– 5(64) + 16 - 32 +2
p(z) = 3072– 1792 – 320 + 16 - 30
p(z) = 1280 – 320 - 14
p(z) = 960 - 14
p(z) = 946
Therefore, p(4) = 946.
You can learn more about Horner's algorithm at
https://brainly.com/question/30547979
#SPJ11
Why are there two solutions for the equation |6 + y| = 2? Explain.
(there should be a solution and an explanation onto why there is two answers)
Answers
|6+y| = 2
If you try -4 you get 2 in a positive form so -4 is one correct.
The second correct one is -8 because 6-8 is -2 but as I was saying before how the absolute value changes it into positive, that means -2 would be switched to 2 meaning that -8 is also a correct answer.
If you need more help just search up what absolute value is.
If you found my answer helpful pls mark has brainliest
Answer:
Sample response: The absolute value symbol in the equation indicates two solutions because absolute value is the distance from a number to zero on a number line. Two different directions, to the right and to the left, will determine the
Step-by-step explanation:
Suppose U(x,y)=x
1/2
y
1/2
and P
x
x+P
y
y=I a. Solve for x
∗
(P
x
,P
y
,I) and y
∗
(P
x
,P
y
,I). b. What are the values of x
∗
(P
x
,P
y
,I) and y
∗
(P
x
,P
y
,I) if I=$24,P
x
=$4 and,P
y
=$2?
Answers
(a) The solutions for x* and y* are given by equations (6) and (7), respectively. (b) When I = $24, Pₓ = $4, and Pᵧ = $2, the optimal values of x* and y* are x* = 16 and y* = 20, respectively.
(a) To solve for x* and y* in terms of Pₓ, Pᵧ, and I, we need to find the utility-maximizing bundle that satisfies the budget constraint.
The utility function is given as U(x, y) = x^(1/2) * y^(1/2).
The budget constraint is expressed as Pₓ * x + Pᵧ * y = I.
To maximize utility, we can use the Lagrange multiplier method. We form the Lagrangian function L(x, y, λ) = U(x, y) - λ(Pₓ * x + Pᵧ * y - I).
Taking the partial derivatives of L with respect to x, y, and λ and setting them equal to zero, we get:
∂L/∂x = (1/2) *\(x^(-1/2) * y^(1/2)\)- λPₓ = 0 ... (1)
∂L/∂y = (1/2) *\(x^(1/2) * y^(-1/2)\) - λPᵧ = 0 ... (2)
∂L/∂λ = Pₓ * x + Pᵧ * y - I = 0 ... (3)
Solving equations (1) and (2) simultaneously, we find:
\(x^(-1/2) * y^(1/2)\)= 2λPₓ ... (4)
\(x^(1/2) * y^(-1/2)\)= 2λPᵧ ... (5)
Dividing equation (4) by equation (5), we have:
\((x^(-1/2) * y^(1/2)) / (x^(1/2) * y^(-1/2))\) = (2λPₓ) / (2λPᵧ)
y/x = Pₓ/Pᵧ
Substituting this into equation (3), we get:
Pₓ * x + (Pₓ/Pᵧ) * x - I = 0
x * (Pₓ + Pₓ/Pᵧ) = I
x * (1 + 1/Pᵧ) = I
x = I / (1 + 1/Pᵧ) ... (6)
Similarly, substituting y/x = Pₓ/Pᵧ into equation (3), we get:
Pᵧ * y + (Pᵧ/Pₓ) * y - I = 0
y * (Pᵧ + Pᵧ/Pₓ) = I
y * (1 + 1/Pₓ) = I
y = I / (1 + 1/Pₓ) ... (7)
Therefore, the solutions for x* and y* are given by equations (6) and (7), respectively.
(b) Given I = $24, Pₓ = $4, and Pᵧ = $2, we can substitute these values into equations (6) and (7) to find the values of x* and y*.
x* = 24 / (1 + 1/2) = 16
y* = 24 / (1 + 1/4) = 20
So, when I = $24, Pₓ = $4, and Pᵧ = $2, the optimal values of x* and y* are x* = 16 and y* = 20, respectively.
Learn more about partial derivatives here:
https://brainly.com/question/32387059
#SPJ11
Suppose U(x,y)=x 1/2 y 1/2 and P x x+P y y=I a. Solve for x ∗ (P x ,P y ,I) and y ∗ (P x ,P y ,I). b. What are the values of x ∗ (P x ,P y ,I) and y ∗ (P x ,P y ,I) if I=$24,P x =$4 and,P y =$2?
If carina can ride her bike at a speed of 7 mph, it will take her 3 hours to travel 21 miles. True or false?
Answers
Answer:
True
Step-by-step explanation:
We know that distance = rate * time
21 miles = 7 miles per hours * 3 hours
21 miles = 21 miles
True
4. a picture can be added to a text in nine different locations on a page. if four different pictures are to be placed in the text, how many different designs are there?
Answers
As per the combination method, there are 3,024 different designs that can be created with four different pictures placed in nine different locations on a page.
There are seven options for the third picture and six options for the fourth picture.
To determine the total number of designs, we can use the multiplication principle, which states that the number of ways two or more independent events can occur together is equal to the product of the number of ways each event can occur individually.
Therefore, the total number of designs that can be created by placing four different pictures in nine different locations on a page can be found by multiplying the number of options for each picture:
9 x 8 x 7 x 6 = 3,024
To know more about combinations here.
https://brainly.com/question/28998705
#SPJ4
what number lies between -2 and -3
Answers
Answer:
-2.5?
Step-by-step explanation:
Consider the exponential function f(x) represented by values in the table.
f(x)
-1.25
-5
-20
-80
-320
X
-1
0
1
2
3
What best describes f(x) on the interval 5 ≤ x ≤ 8 ?
A. negative and decreasing
B. negative and increasing
C. positive and decreasing
D. positive and increasing
Answers
f(x) is negative and decreasing on the interval 5 ≤ x ≤ 8, since the values of f(x) are negative and continue to decrease as x increases. The best answer is A. negative and decreasing.
Describe Function?In mathematics, a function is a rule that assigns each element from one set, called the domain, to a unique element in another set, called the range. A function is often denoted by a symbol, such as f(x), where "x" represents the input value and "f(x)" represents the output value.
The domain of a function is the set of all possible input values, and the range is the set of all possible output values. For example, the function f(x) = x^2 has a domain of all real numbers and a range of all non-negative real numbers.
Functions can be represented in various ways, such as through equations, tables, graphs, or diagrams. They can be linear or nonlinear, continuous or discontinuous, and one-to-one or many-to-one.
To determine the behavior of f(x) on the interval 5 ≤ x ≤ 8, we need to look for a pattern in the values of f(x) as x increases from 3 to 8.
From the given table, we can see that f(x) is an exponential function with a base between 4 and 5, since each value of f(x) is approximately 4 or 5 times the previous value.
Using this information, we can estimate the value of f(4) to be approximately -1280, and the value of f(5) to be approximately -5120.
Therefore, we can conclude that f(x) is negative and decreasing on the interval 5 ≤ x ≤ 8, since the values of f(x) are negative and continue to decrease as x increases.
Thus, the best answer is A. negative and decreasing.
To know more about exponential visit:
https://brainly.com/question/11487261
#SPJ1
Decompose area with triangles the following
Answers
The solution of the given problem of triangle is determined as 55 square miles.
What is a triangle?A triangle is described as a three-sided polygon, which has three vertices of which the three sides are connected with each other end to end at a point, which forms the angles of 180 degrees.
We have that the two triangles with a base of 10 miles and heights of 7 miles and 4 miles can be formed from the composite design.
A triangle's area is found as :
A = (1/2)b* h
where
A = s area,
B = foundation, and
H = height.
We find each triangle's area using the following formula:
Area of 1st triangle(1/2)(10)(7) = 35 square miles
Area of 2nd triangle(1/2)(10)(4) = 20 square miles
The composite shape's surface area is the two triangles combined regions:
(35 + 20) = 55 square miles
In conclusion, the combined size of the two triangles in the shape is 55 square miles.
Learn more about triangle at:
https://brainly.com/question/1058720
#SPJ1
#complete question:
Use decomposition to find the area of the figure.
A drawing of a composite shape made up of two triangles with a common base and the length of the base equals 10 miles. The heights of the two triangles are 7 miles and 4 miles.
what is 6x³-x ×(1-6x+3x)
Answers
Answer:
6x^3 + 3x^2 - x
Step-by-step explanation:
6x^3 - X x (1-3x)
= 6x^3 - x + 3x^2
=6x^3 + 3x^2 - x
(a) Type an equation and (b) solve. Type the answers in the spaces provided.
In the basketball championship game, the Falcons had three fewer than twice as many Bears players. If the Falcons had 11 players, how many players were on the Bears? (Use b as the variable.)
(a)
(b) Bears:
pls, I need help with this. I've tried to do it on my own, but for me, it's pretty difficult.
Answers
Algebra:
G = z-s/r solve for z
Answers
Answer:
z=gr+s/r
Step-by-step explanation:
Hope this helps :)
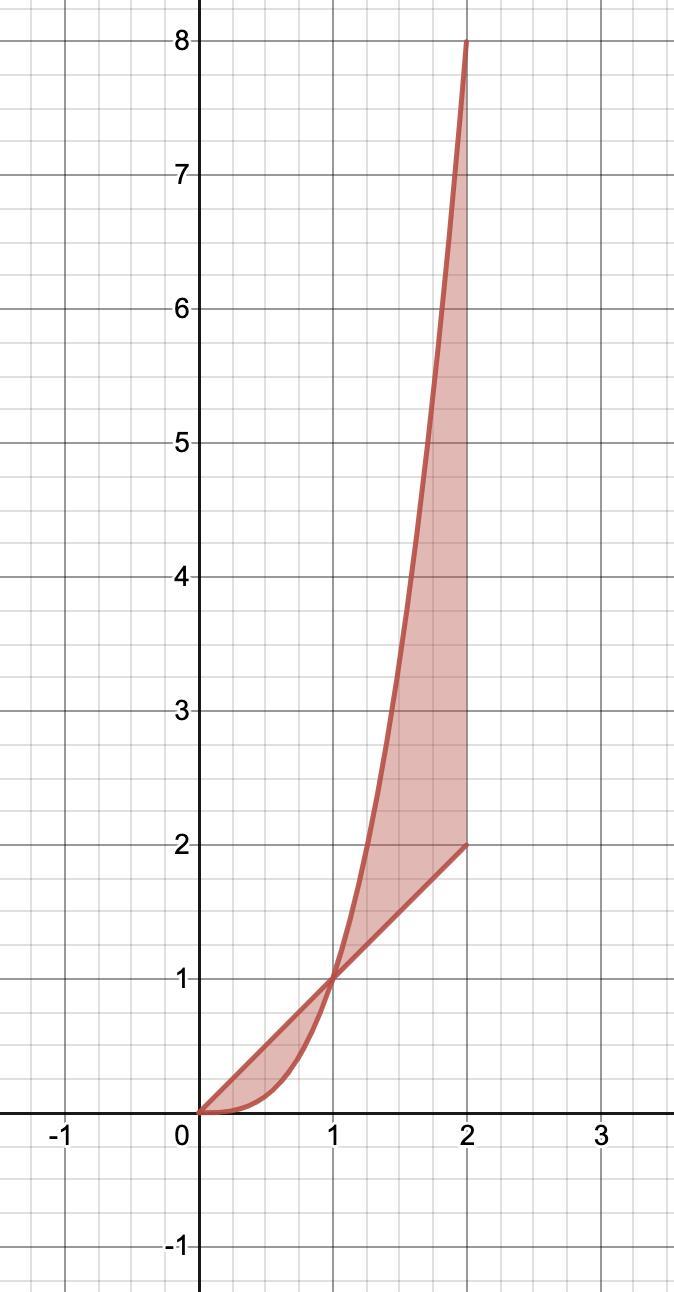
Could anyone help I just need to know how to do part b

Answers
Answer:
k = 408, as shown in your problem statement
Step-by-step explanation:
Compute the integral in the usual way, then compare to the given expression and solve for k. We use the "cylindrical shell" method to find the volume.
The integral that gives the volume is ...
\(\displaystyle V=\int_0^1{2\pi x(x-x^3)}\,dx+\int_1^2{2\pi x(x^3-x)}\,dx\\\\=\dfrac{2\pi(1^3-0^3)}{3}-\dfrac{2\pi(1^5-0^5)}{5}+\dfrac{2\pi(2^5-1^5)}{5}-\dfrac{2\pi(2^3-1^3)}{3}\\\\=2\pi\left(\dfrac{5\cdot1^3-3\cdot1^5+3(2^5-1^5)-5(2^3-1^3)}{15}\right)=\dfrac{2\pi}{15}(5-3+3(31)-5(7))\\\\=\dfrac{\pi}{15}(120)=\dfrac{\pi}{15}(k-9(8^{5/3}))\qquad\text{compare to given expression}\\\\120=k-288\qquad\text{multiply by $15/\pi$ and simplify}\\\\k=408\qquad\text{add 288}\)