The tree diagram below shows all of the possible outcomes for flipping three coins.
What is the probability of one of the coins landing on tails and two of them landing on heads?
A) 1/4
B) 3/8
C) 1/2
D) 3/4

Answers
Answer:
B
Step-by-step explanation:
In that scenario, you would have one T and two H's, in any order. Looking at the chart, this happens in 3 different scenarios. Since there are a total of 8 possible outcomes, the probability of this happening is 3/8 or answer choice B. Hope this helps!
Answer:B
Step-by-step explanation: the number of event is 3 event={HHT, HTH,THH }
And the number of sample space is 8
By using 2^n formula our n is 3 2^3 = 8
The probability = 3/8
Hope it helps
Brainliest please
Related Questions
Factor the trinomial x^2+19x+84
Answers
Answer:
(x+7)(x+12)
Step-by-step explanation:
Hope this helps and have a great day!!!!
what is the square root of 1,000,000,000?
Answers
Unless you need it in square root form
your answer is
31622.7766017
good luck :)
btw can i have brainliest
Bruno had a gross income of $4925 during each pay period last year. If he got
paid monthly, how much of his yearly pay was deducted for FICA?
A. $4521.15
B. $3250.50
C. $3871.05
D. $3841.50

Answers
The amount of Bruno's yearly pay deducted for FICA is approximately
A. $4,524.15. The closest option provided is A. $4521.15.
To calculate the amount of FICA deducted from Bruno's yearly pay, we need to consider the specific FICA tax rates for Social Security and Medicare.
As of 2021, the Social Security tax rate is 6.2% on income up to a certain threshold, and the Medicare tax rate is 1.45% on all income.
Given that Bruno's gross income per pay period is $4925 and he is paid monthly, we can calculate the yearly gross income as follows:
Yearly gross income = $4925 * 12 = $59,100
To calculate the FICA deduction, we need to find the sum of the Social Security and Medicare taxes. Using the respective tax rates mentioned earlier:
Social Security deduction = $59,100 * 6.2% = $3,667.20
Medicare deduction = $59,100 * 1.45% = $856.95
Adding these two deductions together:
FICA deduction = $3,667.20 + $856.95 = $4,524.15
Therefore, the amount of Bruno's yearly pay deducted for FICA is approximately $4,524.15.
The closest option provided is A. $4521.15.
for such more question on amount deducted
https://brainly.com/question/25821437
#SPJ8
pdf Ron, Sue, and Ted arrive at the beginning of a professor’s office hours. The amount of time they will stay is exponentially distributed with means 1, 1/2, and 1/3 hours. (a) What is the expected time until only one student remains? (b) For each student, find the probability they are the last student left. (c) What is the expected time until all three students are gone?
Answers
Answer:
a) 0.45 hours
b)
P( Ron ) = 7/12
P( sue ) = 4/15
P(Ted ) = 3/20
c) 1.22 hours
Step-by-step explanation:
Ron , sue and Ted
mean values = 1, 1/2 , 1/3 hours
a) determine the expected time until only one student remains
E(x) = 9/20 = 0.45 hours
b) Probability that each student is the last student left
P( Ron ) = 7/12
P( sue ) = 4/15
P(Ted ) = 3/20
C) Time until all students are gone
= 146 / 120 = 1.22 hours
attached below is the detailed solution



This question is based on the concept of probability.Therefore, the answers are as follows:
(a) 0.45 hours
\(\bold{(b) \, P(Ron) = \dfrac{7}{12} ,P (Sue) = \dfrac{4}{15} ,P(Ted) = \dfrac{3}{20}\beta}\)
(c) 1.22 hours
Given:
The amount of time they will stay is exponentially distributed with means 1, 1/2, and 1/3 hours.
According to the question,
The amount of time they will stay is exponentially distributed with means 1, 1/2, and 1/3 hours.
(a) The expected time until only one student remains,
\(E(X) = \dfrac{9}{20} = 0.45 \,hours\)
(b) Now, find the probability they are the last student left,
\(P(Ron) = \dfrac{7}{12} \\P (Sue) = \dfrac{4}{15} \\P(Ted) = \dfrac{3}{20}\)
(c) The expected time until all three students are gone is,
\(= \dfrac{146}{120} \\\\= 1.22 hours\)
Therefore, the answers are as follows:
(a) 0.45 hours
\((b) P(Ron) = \dfrac{7}{12} ,P (Sue) = \dfrac{4}{15} ,P(Ted) = \dfrac{3}{20}\beta\)
(c) 1.22 hours
For more details, prefer this link:
https://brainly.com/question/23044118
A convex lens with focal length f centimeters will project the image of an object on a
point behind the lens. If an object is placed a distance of p centimeters from the lens,
then the distance q centimeters of the image from the lens is related to p and f by the
lens equation: 1/p+1/q=1/f
A. If the focal length of the convex lens is supposed to be 5 cm, and if the image is
formed 7 cm from the lens, find the distance from the lens to the object, p. (It’s not necessary to simplify your answer.)
B. Find an expression that gives q as a function of p, assuming that the focal length is a constant of 5 centimeters.
C. Sketch a graph of q as a function of p (i.e., q(p)), assuming that the focal length is a
constant of 5 centimeters. Show any important features of the graph.
D. Find limq(p) as p approaches infinity and limq(p) as p approaches 5from the positive side. What do these limits represent physically? What must
happen to the distance of the image and the object?
Answers
Answer:
A. Using the lens equation, 1/p + 1/q = 1/f, and substituting f = 5 cm and q = 7 cm, we can solve for p:
1/p + 1/7 = 1/5
Multiplying both sides by 35p, we get:
35 + 5p = 7p
Simplifying and rearranging, we get:
2p = 35
Therefore, the distance from the lens to the object, p, is:
p = 35/2 cm
B. Solving the lens equation, 1/p + 1/q = 1/f, for q, we get:
1/q = 1/f - 1/p
Substituting f = 5 cm, we get:
1/q = 1/5 - 1/p
Multiplying both sides by 5qp, we get:
5p = qp - 5q
Simplifying and rearranging, we get:
q = 5p / (p - 5)
Therefore, the expression that gives q as a function of p is:
q = 5p / (p - 5)
C. Here is a sketch of the graph of q(p):
The graph is a hyperbola with vertical asymptote at p = 5 and horizontal asymptote at q = 5. The image distance q is positive for object distances p greater than 5, which corresponds to a real image. The image distance q is negative for object distances p less than 5, which corresponds to a virtual image.
D. Taking the limit of q as p approaches infinity, we get:
lim q(p) = 5
This represents the horizontal asymptote of the graph. As the object distance becomes very large, the image distance approaches the focal length of the lens, which is 5 cm.
Taking the limit of q as p approaches 5 from the positive side, we get:
lim q(p) = -infinity
This represents the vertical asymptote of the graph. As the object distance approaches the focal length of the lens, the image distance becomes infinitely large, indicating that the lens is no longer able to form a real image.
In order for the lens to form a real image, the object distance p must be greater than the focal length f. When the object distance is less than the focal length, the lens forms a virtual image.
Solve for the values of x for each of the following exponential equations and inequalities.
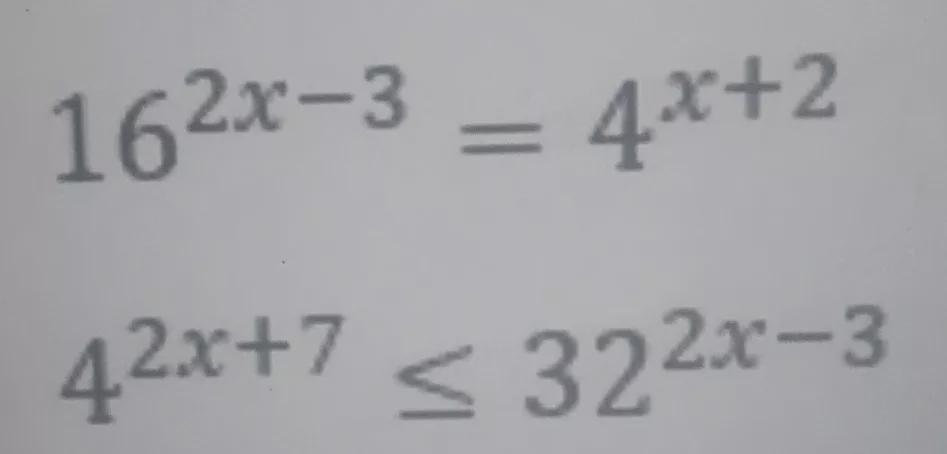
Answers
Given:
The exponential equation is,
a)
\(16^{2x-3}=4^{x+2}\)Solve the equation,
\(\begin{gathered} 16^{2x-3}=4^{x+2} \\ 4^{2(2x-3)}=4^{x+2} \\ \Rightarrow2(2x-3)=x+2 \\ 4x-6=x+2 \\ 4x-x=2+6 \\ 3x=8 \\ x=\frac{8}{3} \end{gathered}\)Answer: x = 8/3.
b) The inequality is,
\(4^{2x+7}\leq32^{2x-3}\)Solve the inequality,
\(\begin{gathered} 4^{2x+7}\leq32^{2x-3} \\ 2^{2(2x+7)}\leq2^{5(2x-3)} \\ \Rightarrow2(2x+7)\leq5(2x-3) \\ 4x+14\leq10x-15 \\ 14+15\leq10x-4x \\ 29\leq6x \\ \frac{29}{6}\leq x \\ x\ge\frac{29}{6} \end{gathered}\)Answer:
\(x\ge\frac{29}{6}\)
What is the equation of the line that is parallel to the line y = x + 4 and passes through the point (6, 5)?
y = x + 3
y = x + 7
y = 3x – 13
y = 3x + 5
Answers
Answer:
y = x - 1
Step-by-step explanation:
Slope = 1
b = 5 - (1)(6)
b = -1
f(m) = 3/5 m + 5 find for f(50)
Answers
Answer:
To find f(50), we need to substitute 50 for m in the function f(m) = (3/5)m + 5:
f(50) = (3/5)(50) + 5
f(50) = 30 + 5
f(50) = 35
Therefore, f(50) is equal to 35.
The value of f for m equals 50 will be 35.
This is a basic arithmetic problem where we just need to put the values given in the question and solve using the PEMDAS rule
given, m = 50
problem, f(m) = 3/5 m + 5
putting the value of m in the problem we get
f(50) = 3/5 (50) + 5
so multiplying 3 (the numerator) by 50, we get:
f(50) = 150/5 + 5
then we divide 150 by 5 and we get:
f(50) = 30 + 5
then by adding 30 and 5 we get the answer:
f(50) = 35
To get more information about PEMDAS,
https://brainly.com/question/11421179
On Monday, Ray had $153.75 in his bank account. On Tuesday, he withdrew $71.00 from his account. After depositing #292.50 on Wednesday, how much money did Ray have in his account
Answers
Answer:
$375.25
Step-by-step explanation:
\(===========================================\)
Withdrew- taking out money (-)
Deposit- putting in money (+)
\(===========================================\)
Ray started off with 153.75. He withdraws (-) 71.
\(153.75-71=82.75\)
Then he deposits (+) 292.5.
\(82.75+292.5=375.25\)
That's your answer!
I hope this helps ❤
The mean of the numbers 15, 21, 17.26. 18,29
is 21. Calculate the standard deviation of the
numbers
Answers
Answer:
6
Step-by-step explanation:
=15+21+17+26+18+29/
/ 21
=126/21
=6
Algebra Question
Let v = (-7,6,-6) and w = (-5,-3,-6) be vectors in R^3. Find the orthogonal projection of v onto w.
Answer:
Projection on w: (-54/14, -159/70, -159/35)
I have the correct answer but I don't know how they got it.
Answers
The orthogonal projection of vector v onto vector w in R^3 is (-54/14, -159/70, -159/35).
To find the orthogonal projection of v onto w, we need to calculate the scalar projection of v onto w and multiply it by the unit vector of w. The scalar projection of v onto w is given by the formula:
proj_w(v) = (v⋅w) / (w⋅w) * w
where ⋅ denotes the dot product.
Calculating the dot product of v and w:
v⋅w = (-7)(-5) + (6)(-3) + (-6)(-6) = 35 + (-18) + 36 = 53
Calculating the dot product of w with itself:
w⋅w = (-5)(-5) + (-3)(-3) + (-6)(-6) = 25 + 9 + 36 = 70
Now, substituting these values into the formula, we have:
proj_w(v) = (53/70) * (-5,-3,-6) = (-54/14, -159/70, -159/35)
Therefore, the orthogonal projection of v onto w is (-54/14, -159/70, -159/35).
In simpler terms, the orthogonal projection of v onto w can be thought of as the vector that represents the shadow of v when it is cast onto the line defined by w. It is calculated by finding the component of v that aligns with w and multiplying it by the direction of w. The resulting vector (-54/14, -159/70, -159/35) lies on the line defined by w and represents the closest point to v along that line.
for such more questions on vector
https://brainly.com/question/15519257
#SPJ8
A rectangle has a length 3x + 1 of and a width of Write an expression for the 3-9
perimeter of the rectangle.
Answers
The expression for the perimeter is P = 12x - 16
How to write an expression for the perimeter?The given parameters are
Length = 3x + 1
Width = 3x - 9
The perimeter is calculated as
P = 2 * (Width + Length)
So, we have
P = 2 * (3x + 1 + 3x - 9)
Evaluate
P = 2* (6x - 8)
Expand
P = 12x - 16
Hence, the expression for the perimeter is P = 12x - 16
Read more about perimeter at:
https://brainly.com/question/19819849
#SPJ1
aman şego şego...... ....
Answers
sego........ ... sego segó
Help me out pls,
20 points!

Answers
Answer:
75.5 is not equivalent because 75 1/2% to a decimal is 0.775
Step-by-step explanation:
Hope this helps
Answer:
OPTION B the correct answer.
\(75 \frac{1}{2}\% = \frac{151}{200} \)
\( = 0.755\)
Help plssss i beg i'm lost

Answers
2. 2/3>2/6
These are just some possible answers, this question is super open-ended :)
Which equations are true for x = –2 and x = 2? Select two options x2 – 4 = 0 x2 = –4 3x2 + 12 = 0 4x2 = 16 2(x – 2)2 = 0
Answers
The equations that are true for x = -2 and x = 2 are x² + 4 = 0 and 4x² = 16. So, the correct option is A) and D).
To determine which equations are true for x = -2 and x = 2, we simply substitute these values into each equation and check if the equation is true or not. Here are the results
x² - 4 = 0
Substituting x = -2 gives (-2)² - 4 = 0, which is true. Substituting x = 2 gives 2² - 4 = 0, which is also true. Therefore, this equation is true for both x = -2 and x = 2.
x² = -4
Substituting x = -2 gives (-2)² = -4, which is not true. Substituting x = 2 gives 2² = -4, which is also not true. Therefore, this equation is not true for either x = -2 or x = 2.
3x² + 12 = 0
Substituting x = -2 gives 3(-2)² + 12 = 0, which is true. Substituting x = 2 gives 3(2)² + 12 = 24, which is not equal to zero. Therefore, this equation is true for x = -2 but not for x = 2.
4x² = 16
Substituting x = -2 gives 4(-2)² = 16, which is true. Substituting x = 2 gives 4(2)² = 16, which is also true. Therefore, this equation is true for both x = -2 and x = 2.
2(x - 2)² = 0
Substituting x = -2 gives 2(-2 - 2)² = 0, which is true. Substituting x = 2 gives 2(2 - 2)² = 0, which is also true. Therefore, this equation is true for both x = -2 and x = 2.
Therefore, the two equations that are true for both x = -2 and x = 2 are x² - 4 = 0 and 4x² = 16. So, the correct answer is A) and D).
To know more about substitution:
https://brainly.com/question/30284922
#SPJ1
2. Kasie lives in Seattle. She can see her house from the observation deck of the Seattle Space Needle. The
observation deck is 520 feet above the ground and the angle of depression from the deck to her house
is 70. What is the direct distance from the base of the Space Needle to Kasie's house? Round your
answer to the nearest foot.
Answers
Direct distance from the base of the Space Needle to Kasie's house = 1429 feet.
What is angle of depression?The angle of depression is the angle between the horizontal line and the observation of the object from the horizontal line. It is basically used to get the distance of the two objects where the angles and an object's distance from the ground are known to us.
Given,
Height of the observation deck AB = 520 feet
Angle of depression = 70°
Distance of the Space needle base to house BC = ?
By the figure,
tan70° = AB/BC
BC = tan70°(AB)
BC = 2.7475(520)
BC = 1428.7 feet
Distance of the Space needle base to house to nearest foot = 1429 feet
Hence, 1429 feet is the distance between base of the Space Needle to Kasie's house.
Learn more about angle of depression here:
https://brainly.com/question/13514202
#SPJ1

I NEED HELP NOWWWW AND I MEAN RIGHT THIS SECOND PLEASE

Answers
Answer: See below
Step-by-step explanation:
1 1/2 as mixed fraction = 3/2
3/4 + 3/4 = 3/2
2 2/3 as a mixed fraction = 8/3
7/3 + 1/3 = 8/3
A company has a policy of retiring company cars; this policy looks at the number of miles driven, the purpose of trips, style of car, and other features. The distribution of the number of months in service for the fleet of cars is bell-shaped and has a mean of 42 months and a standard deviation of 10 months. Using the 68-95-99.7 rule, what is the approximate percentage ofcars that remain in service between 52 and 72 months.
Answers
EXPLANATION
We have the following facts:
Mean = 42
Standard Deviation = 10
We can see that 52 is 1 standard deviation to the right of the mean.
Furthermore, 72 is 3 standard deviations to the right of the mean.
Also, the Empirical Rule has 68% between 1 standard deviation and 34% on one side. Additionally, it has 95% between two standard deviations or 47.5% on one side.
Moreover, It has 99.7% within 3 sd or 49.85% on one side.
Following this reasoning, we can affirm that between 3 standard deviations and 1 standard deviation there are 49.85-34=15.85%
Simplify the variable expression by evaluating its numerical part, and enter
your answer below.
(48-17) - w
Answer here
SUBMIY
Answers
The simplified version of the expression would be 31-w
The numerical part of the expression given is :
48-17Simplifying using Subtraction operation:
48-17 = 31Adding the alphabetical part :
31 - wTherefore, the simplified form of the expression is 31-w.
Learn more on equations :https://brainly.com/question/2972832
#SPJ1
What is the absolute max on the closed interval [0,1]?
![What is the absolute max on the closed interval [0,1]?](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/sQ5nVptUqLv6WKnAQOUw5Fl7ZETCFgBU.jpeg)
Answers
Check the picture below.
![What is the absolute max on the closed interval [0,1]?](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/qs3EY1M5YDxFTHG0grEeDKNBQPSZkyZP.png)
The slope is m=2...y-intercept, b=5.
What would be the equation?
Answers
what is the answer? help me

Answers
solve the equation 3+6= -1x+6
Answers
Answer:
x = -3
Step-by-step explanation:
3 + 6 = 9
9 = -1x + 6
-1x = 9 - 6 = 3
x = -3
Answer:
x = -3
Step-by-step explanation:
QUICK! 40 points. Consider this cone with the diameter measure of 17 inches.
A cone with diameter 17 inches and slant height of 22 inches.
What is the surface area of the cone?
SA = Pir2 + Pirl
A. 204Pi in.2
B. 259.25Pi in.2
C. 446.25Pi in.2
D. 663Pi in.2

Answers
259.25π in² is the surface area of the cone
The surface area of a cone can be calculated using the formula SA = πr² + πrl
where r is the radius and l is the slant height.
Given that the diameter is 17 inches, the radius (r) is half of the diameter, which is 17/2 = 8.5 inches.
The slant height (l) is given as 22 inches.
Substituting these values into the formula:
Surface Area = π(8.5)² + π(8.5)(22)
= 72.25π + 187π
= 259.25π
Therefore, the surface area of the cone is 259.25π in²
To learn more on Three dimensional figure click:
https://brainly.com/question/2400003
#SPJ1
The sum of two consecutive integers is −29. Find the integers.
Answers
Answer:
the two consecutive integers are 6 and 7.
Step-by-step explanation:
Im %99 sure
In a class of students, the following data
table summarizes how many students have a
cat or a dog. What is the probability that a
student chosen randomly from the class has
a cat?
Has a dog
Does not have a
dog
Has a cat
2
3
Does not have a
cat
12
10
Answers
The table can be summarized as follows:
| | Has a dog | Does not have a dog |
|----------|-----------|---------------------|
| Has a cat | 2 | 3 |
| Does not have a cat | 12 | 10 |
To find the probability that a student chosen randomly from the class has a cat, we need to find the total number of students who have a cat (regardless of whether or not they have a dog), and divide it by the total number of students in the class.
The number of students who have a cat is 2 (those who have a dog and a cat) + 3 (those who have a cat but do not have a dog) = 5.
The total number of students in the class is the sum of all four categories: 2 (has a cat and a dog) + 3 (has a cat, does not have a dog) + 12 (does not have a cat, has a dog) + 10 (does not have a cat, does not have a dog) = 27.
So, the probability that a student chosen randomly from the class has a cat is 5/27.
45 minutes and 45 minutes is 90 Minutes so that is 1 hour and 30 minutes. So the answer is your welcome I’m so high
Answers
Answer:
Yeah that's correct.
Step-by-step explanation:
You're welcome I'm so high
K Graph the function f(x) = -x² +6. f(x) X -2 - 1 0 1 2 TE Complete the table of function values below. f(x) X - 2 - 1 0 1 2
Answers
Answer:
Step-by-step explanation:
Here is the completed table of function values for f(x) = -x² + 6:
x -2 -1 0 1 2
f(x) -2 5 6 5 2
To graph the function, you can plot the points from the table on a coordinate plane and connect them with a smooth curve. The graph of f(x) = -x² + 6 is a downward-facing parabola that opens up to the point (0, 6), as shown below:
7
|
|
|
|
|
|
|
|
-----0------
|
|
|
|
|
|
|
|
-2
The vertex of the parabola is located at the point (0, 6), and the axis of symmetry is the vertical line x = 0.
Long division: 2/ 2769
Answers
Answer:
1384.5
Step-by-step explanation
Diviseion is just the oppisite of multiplication so you can think to yourself that what times two equals 2769. If you multiply 1384.5 on a calculater you get 2769.