The total profit made by an engineering firm is given by the function p=x^2 - 24x +5000 where x is the number of clients the firm has and p is the profit.
1. Find the maximum profit made by the company.
2. How many clients are necessary to reach the profit outlined in part one?
Answers
Answer:
\(5144\)
\(12\)
Step-by-step explanation:
The function \(p=x^2-24x+5000\) is incorrect as its roots are imaginary \(b^2-4ac=576-4\times 5000=-19424<0\).
So, the correct function is
\(p=-x^2+24x+5000\)
Differentiating with respect to \(x\) we get
\(p'=-2x+24\)
Equating with zero
\(0=-2x+24\\\Rightarrow x=\dfrac{24}{2}\\\Rightarrow x=12\)
Double derivative of the function
\(p''=-2<0\)
So, the function is maximum at \(x=12\)
Maximum profit is
\(p=-x^2+24x+5000=-12^2+24\times 12+5000\\\Rightarrow p=5144\)
The maximum profit made by the company is \(5144\)
The number of clients required to make the maximum profit is \(12\).
Related Questions
solve for x : 8 (2-x) +3x= -4
Answers
Answer:
\(x=4\)
Step-by-step explanation:
So we have the equation:
\(8(2-x)+3x=-4\)
Distribute the first term:
\(16-8x+3x=-14\)
Combine like terms:
\(16-5x=-4\)
Subtract 16 from both sides:
\(-5x=-20\)
Divide both sides by -5:
\(x=4\)
So, the value of x is 4 :)
A baker makes 60 muffins. He sells 24 of the muffins.
He put the rest of the muffins in boxes. Each box can hold 4 muffins.
Which equation can be used to find b, the number of boxes the baker will need?
OA.
B.
OC.
OD. (60
60+ 24 ÷ 4 = b
60 24 ÷ 4 = b
-
(60+24) ÷ 4 = b
24) = 4 = b
-

Answers
Answer:c
Step-by-step explanation:
c
Answer:b
Step-by-step explanation:
a circular window with a diameter of 26 inches is being installed over a door. the wall with the dor and window is 18 feet high. the door is 80inches from the floor to the top of the dooor. what is the distance from the cieling to the top of the window?
Answers
Answer:
24 inches
Step-by-step explanation:
First, we need to convert the height of the wall to inches since the diameter of the window is given in inches:
18 feet = 18 x 12 inches = 216 inches
Next, we can find the distance from the floor to the top of the window by subtracting the height of the door from the height of the wall and then dividing by 2 (since the window will be centered above the door):
Distance from floor to top of window = (216 inches - 80 inches) / 2 = 68 inches
Finally, we can use the Pythagorean theorem to find the distance from the ceiling to the top of the window. We can consider the triangle formed by the height of the wall, the distance from the floor to the top of the door, and the distance from the floor to the top of the window. We can let x be the distance from the floor to the top of the window, then we have:
x^2 + 80^2 = 216^2
Simplifying this equation, we get:
x² = 216² - 80²
x² = 43,296 - 6,400
x² = 36,896
x = \(\sqrt{36,896}\) = 192 inches
Therefore, the distance from the ceiling to the top of the window is:
Distance from ceiling to top of window = 216 inches - 192 inches = 24 inches
So the distance from the ceiling to the top of the window is 24 inches.
on a piece of paper, graph f(x)= {x if x<2 2 if x>2}
Answers
Answer:
see below
Step-by-step explanation:
The graph has two parts. There is one line for x < 2. It has a slope of 1 and a y-intercept of 0.
The line for x > 2 is the horizontal line x=2.
The point at x=2 is not defined by the function you have posted here, so there is a "hole" in the graph at that point.

Answer:
the person above is correct
Step-by-step explanation:
:p
As the CAPS document outlines, the Content Specification and Content Clarification for Patterns, Functions, and Algebra shows sequenced mathematics content topics and a content area spread. In the Intermediate Phase, select one topic and report on the topic sequence and content area spread. Your report should demonstrate mathematics concepts and procedures’ hierarchical and logical progression.
Answers
Answer:
Step-by-step explanation:
In the Intermediate Phase of mathematics education, one topic that demonstrates a hierarchical and logical progression in patterns, functions, and algebra is the concept of "Linear Equations."
The topic of Linear Equations in the Intermediate Phase builds upon the foundation laid in earlier grades and serves as a stepping stone towards more advanced algebraic concepts. Here is an overview of the topic sequence and content area spread for Linear Equations:
Introduction to Variables and Expressions:
Students are introduced to the concept of variables and expressions, learning to represent unknown quantities using letters or symbols. They understand the difference between constants and variables and learn to evaluate expressions.
Solving One-Step Equations:
Students learn how to solve simple one-step equations involving addition, subtraction, multiplication, and division. They develop the skills to isolate the variable and find its value.
Solving Two-Step Equations:
Building upon the previous knowledge, students progress to solving two-step equations. They learn to perform multiple operations to isolate the variable and find its value.
Writing and Graphing Linear Equations:
Students explore the relationship between variables and learn to write linear equations in slope-intercept form (y = mx + b). They understand the meaning of slope and y-intercept and how they relate to the graph of a line.
Systems of Linear Equations:
Students are introduced to the concept of systems of linear equations, where multiple equations are solved simultaneously. They learn various methods such as substitution, elimination, and graphing to find the solution to the system.
Word Problems and Applications:
Students apply their understanding of linear equations to solve real-life word problems and situations. They learn to translate verbal descriptions into algebraic equations and solve them to find the unknown quantities.
The content area spread for Linear Equations includes concepts such as variables, expressions, equations, operations, graphing, slope, y-intercept, systems, and real-world applications. The progression from simple one-step equations to more complex systems of equations reflects a logical sequence that builds upon prior knowledge and skills.
By following this hierarchical progression, students develop a solid foundation in algebraic thinking and problem-solving skills. They learn to apply mathematical concepts and procedures in a systematic and logical manner, paving the way for further exploration of patterns, functions, and advanced algebraic topics in later phases of mathematics education.
Find the partial derivative of the function f(x,y)=Integral of cos(-7t^2-6t-1)dt. Find fx(x,y) and fy(x,y)
Answers
Answer:
\(\mathbf{\dfrac{\partial f}{\partial x}= cos (-7x^2 -6x - 1)}\)
\(\mathbf{\dfrac{\partial f}{\partial y}= cos ( -7y^2 -6y-1)}\)
Step-by-step explanation:
Given that :
\(f(x,y) = \int ^x_y cos (-7t^2 -6t-1) dt\)
Using the Leibnitz rule of differentiation,
\(\dfrac{d}{dt} \int ^{b(t)}_{a(t)} f(x,t) dt= f(b(t),t) *b'(t) -f(a(t),t) * a' (t) + \int^{b(t)}_{a(t)} \dfrac{\partial f}{\partial t} \ dt\)
To find: fx(x,y)
\(\dfrac{\partial f}{\partial x}= \dfrac{\partial }{\partial x} [ \int ^x_y cos (-7t^2 -6t -1 ) \ dt]\)
\(\dfrac{\partial f}{\partial x}= \dfrac{\partial x}{\partial x} cos (-7x^2 -6x -1 ) - \dfrac{\partial y}{\partial x} * cos (-7y^2 -6y-1) + \int ^x_y [\dfrac{\partial }{\partial x} \ \{cos (-7t^2-6t-1)\}] \ dt\)
\(\dfrac{\partial f}{\partial x}= cos (-7x^2 -6x - 1) -0+0\)
\(\mathbf{\dfrac{\partial f}{\partial x}= cos (-7x^2 -6x - 1)}\)
To find: fy(x,y)
\(\dfrac{\partial f}{\partial y}= \dfrac{\partial }{\partial y} [ \int ^x_y cos (-7t^2 -6t -1 ) \ dt]\)
\(\dfrac{\partial f}{\partial y}= \dfrac{\partial x}{\partial y} cos (-7x^2 -6x -1 ) - \dfrac{\partial y}{\partial y} * cos (-7y^2 -6y-1) + \int ^x_y [\dfrac{\partial }{\partial y} \ \{cos (-7t^2-6t-1)\}] \ dt\)
\(\dfrac{\partial f}{\partial y}= 0 - cos ( -7y^2 -6y-1)+0\)
\(\mathbf{\dfrac{\partial f}{\partial y}= cos ( -7y^2 -6y-1)}\)
What is the best description of originality?
nonobvious
special or interesting
convergent
having a low probability, unique
Answers
Originality is the quality of being unique, new, and innovative. It requires creativity, imagination, inspiration, and nonobviousness. Special or interesting aspects may be present, but they are not sufficient to define originality.
Originality refers to the quality of being unique, new, and innovative. It involves creating something that has not been seen or experienced before. The best description of originality is that it is having a low probability and being unique.
An original idea, product, or work of art is something that has not been copied or imitated from others. It represents a new perspective or approach that can offer a fresh insight into a problem or challenge. Originality requires a high level of creativity, imagination, and inspiration, as well as a willingness to take risks and explore new possibilities.
Nonobviousness is also an important factor in originality. It means that the idea or invention is not something that would be obvious to someone skilled in the same field or industry. In other words, an original idea should not be something that could be easily predicted or anticipated.
Special or interesting are also characteristics of originality, but they are not sufficient to define it. An idea or product can be special or interesting without being truly original. For example, a new flavor of ice cream may be interesting, but it may not be original if it has already been created by someone else.
Convergent thinking, on the other hand, involves finding a single solution to a problem. It is the opposite of divergent thinking, which involves generating multiple ideas and possibilities. Convergent thinking is important for finding effective solutions to problems, but it is not the same as originality.
In conclusion, originality is the quality of being unique, new, and innovative. It requires creativity, imagination, inspiration, and nonobviousness. Special or interesting aspects may be present, but they are not sufficient to define originality.
To know more about Originality.
https://brainly.com/question/31916017
#SPJ11
help with 6 please i need to graduate
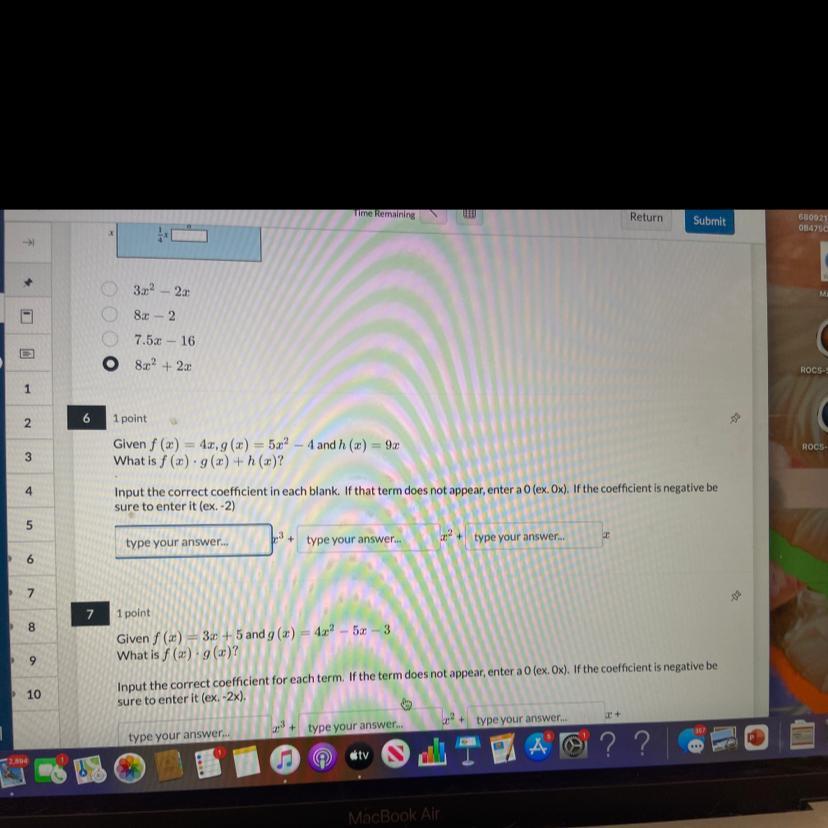
Answers
The expression with the correct coefficients in each block is given as follows:
20x³ + 0x² - 7x.
How to obtain the resultant function?The functions in the context of this problem are defined as follows:
f(x) = 4x.g(x) = 5x² - 4.h(x) = 9x.The operation is given as follows:
f(x)g(x) + h(x).
Hence, to obtain the resultant function, we apply the definitions into the operation and the simplify, applying the distributive property and combining the like terms, as follows:
4x(5x² - 4) + 9x = 20x³ - 16x + 9x = 20x³ - 7x.
As there is no x² term, the coefficient of zero multiplies the term x².
More can be learned about functions at https://brainly.com/question/31895757
#SPJ1
What is the product of (3+square root of 7)(3-square root of 7)
Answers
( 3 + √ 7 ) ( 3 − √ 7 ) = 2 Explanation: You can simplify this expression by using the formula for the difference of squares a 2 − b 2 = ( a − b ) ( a + b ) In your case, you ca say that a = 3 and b = √ 7 . This means that you have ( 3 + √ 7 ) ( 3 − √ 7 ) = 3 2 − ( √ 7 ) 2 = 9 − 7 = 2 Alternatively, if you don't know the formula for the difference of squares, you can rewrite this expression by expanding the parantheses ( 3 + √ 7 ) ( 3 − √ 7 ) = 3 ⋅ 3 − 3 ⋅ √ 7 + 3 ⋅ √ 7 − √ 7 ⋅ √ 7 Once again, the result will be 3 ⋅ 3 − √ 7 ⋅ √ 7 = 3 2 − 7 = 2
1 Josiah is making a candle by pouring melted wax into a mold in the shape of a square pyramid. Each side of the base of the pyramid is 12 in and the height of the pyramid is 14in. To get the wax for the candle, Josiah melts cubes of wax that are each 6 in by 6 in by 6 in. How many of the wax cubes will Josiah need in order to make the candle? Show your work.
Answers
Answer:
3.11 wax cubes
Step-by-step explanation:
5 rubber stamp cost $9.70. Which equation would help determine the cost of 11 rubber stamps
Answers
Answer:
21.34 for 11 stamps. 1.94x=21.34. x could be any number but in this problem it would be 11.
Step-by-step explanation:
9.70/5=1.94
1.94/per stamp
1.94*11=21.34
Answer:
The equation you would use for this problem is: $9.70/5=Px11.
Step-by-step:
We know that 5 rubber stamps costs $9.70, so we need to find out how much just 1 eraser will cost. So we will do $9.70 divided by 5... once you figure out what $9.70/5 is you are going to take that number and multiply it by 11 to get the total cost of 11 erasers.
What is one over two to the fifth power?
Answers
Answer:0.03125
Step-by-step explanation:
GOO*OOGLE
Step-by-step explanation:
(1/2)^5 = 1/2 * 1/2 * 1/2 * 1/2 * 1/2 = 1/32
Please help me out
This is due today and I cant get it done

Answers
- The wait times for two different rides are
shown in the table. If there are 120 people in
line for the swings, how long can you expect
to wait to ride the ride?
Ride
Wait Times...
-Carousel
6 minutes for 48 people in line
-Swings
12 minutes for 75 people in line
Answers
Answer:
(in a fraction format) 12/75=x/120
Step-by-step explanation:
The simplest way I can explain* is for these types of problems, all you do is make an equation like the one above and use an X as the numerator in the second equation over the denominator, which should be something like 120 in this problem. So after you find the information for the problem, which is the part where it states how much time a line of 48 people had to wait, make an equation using that information, which is 12/48. Then to finish the equation, use the 120 people in line part and make another equation that has an X as the numerator, or the number on top. It should look like this:
12/75 = x/120
I tried sorry*
How can you use standard deviations to compare the spread of each data set?
Sample A: 2,5,1,2,3,3,4,3
Sample b: 10,5,1,2,3,7,4,3
Answers
Calculate the standard deviation for each data set:
Sample A = 1.246
Sample B = 2.924
The smaller the deviation the closer the data set is, the larger the deviation the more widespread the data set is.
Sample B has a larger deviation so the spread of the data is wider.
What should be the third row in the following series of shapes

Answers
Answer:
The answer is number 2
At an amusement park, riders must be at least 48 inches tall to ride the Night Eagle roller coaster. Keenan has grown 1.5 inches since last summer, but he is still too short to ride. Let x represent how tall Keenan was last summer. Which inequality describes the problem?
Answers
The inequality that describes the given word problem is;
x + 1.5 < 48
How to solve Inequality word problems?Let x represent how tall Keenan was last summer. Thus;
x = Keenan's height last summer in inches
If he was x inches last summer, and has since grown an additional 1.5 inches up to date, then it means that his total height now is;
x + 1.5 inches.
The conditons state "riders must be at least 48 inches tall to ride the Night Eagle roller coaster". So it means that his height must be equal to 48 inches, or larger than 48 inches, to make him eligible to ride the roller coaster.
But since he is still too short to ride, this means the expression x+1.5 is smaller than 48 and as such the inequality of this problem is;
x + 1.5 < 48
Read more about Inequality Word Problems at; https://brainly.com/question/25275758
#SPJ1
HELLLP !!!!!!
What is the product

Answers
Answer:
Please mark as Brainliest :)
Step-by-step explanation:

How do you write 27.346 as decimal
Answers
it's already a decimal lma.o
Simplify.
2
5x² - 7x + 3
-
10
+ 8x² + 9x
I need help
Answers
Answer:
621 i guess
Step-by-step explanation:
18x² + 2x² - 7
Tap on a clip to paste it in the text box.
Solve for the rate (as a %). Round to the nearest tenth of a percent when necessary. What is the rate if the base is 366 and the portion is 50?
Answers
Answer:
\(\Huge \boxed{\text{13.66$\%$}}\)
Step-by-step explanation:
To find the rate, we need to use the following formula:
\(\LARGE \boxed{ \boxed{\text{Rate = $\frac{\text{Portion}}{\text{Base}}$$\times$100}}}\)
Where "Portion" is the part of the whole and "Base" is the whole.
Now, let's plug in the given values:
\(\large \text{Rate = $\frac{\text{50}}{\text{366}}$$\times$100 = 13.66 (Rounded to the nearest tenth of a percent)}\)
Therefore, the rate is 13.66% (rounded to the nearest tenth of a percent).
----------------------------------------------------------------------------------------------------------
Find the equation of the tangent line at the given point on the following curve.
x² + y² = 25, (-4,-3)
The equation of the tangent line to the point (-4,-3) is y=
Answers
y
=
3
4
x
+
25
4
.
The first term of a geometric sequence is 5 and the multiplier, or ratio, is –2. What is the sum of the first 5 terms of the sequence?
Answers
Step-by-step explanation:
s1 = 5
s2 = s1 × -2 = 5×-2 = -10
s3 = s2 × -2 = -10 × -2 = 20
...
now, we could do all that manually.
but there is also a formula for geometric sequence.
in fact, there are 2 - one for finite and one for infinite sequences.
and I was not completely honest, each of these 2 had some sub-forms depending on the size of the multiplier or ratio.
since we need the sum of the first 5 terms, which of the 2 do you think we need ?
of course, finite, because 5 is a normal number we can "touch". it is not infinity.
so, the formulas for finite sums of geometric sequences are :
if |r| < 1, Sn = a(1 - r^n)/(1 - r)
if |r| > 1, Sn = a(r^n - 1)/(r - 1)
if r = 1, Sn = na
if r = -1, then Sn = a or 0 depending on if n is odd or even.
the sequence is in general
s1 = a
sn = sn-1 × r
in our case a = 5, r = -2.
so, what form of the formula do we need ?
|-2| = 2, and 2 > 1, so ...
S5 = 5(-2^5 ‐ 1)/(-2 - 1) = 5(-32 - 1)/-3 = 5×-33/-3 =
= 5 × 11 = 55
quick check, as the 5 terms are
5
-10
20
-40
80
and their sum is : 55
correct !
4z - 15 = 4z + 11
What does Z=
Answers
implifying
4z + -15 = 4z + 11
Reorder the terms:
-15 + 4z = 4z + 11
Reorder the terms:
-15 + 4z = 11 + 4z
Add '-4z' to each side of the equation.
-15 + 4z + -4z = 11 + 4z + -4z
Combine like terms: 4z + -4z = 0
-15 + 0 = 11 + 4z + -4z
-15 = 11 + 4z + -4z
Combine like terms: 4z + -4z = 0
-15 = 11 + 0
-15 = 11
Solving
-15 = 11
Use the given zero to find the remaining zeros of the polynomial function.
P(x) = 2x3 − 5x2 + 6x − 2; 1 + i
Answers
Using the given zero . The three zeros of the polynomial function are 1 + i, 1 - i, 1/2, and 2.
What is the polynomial function?If 1 + i is a zero of the polynomial function P(x), then its conjugate, 1 - i, must also be a zero of the polynomial, since complex zeros of polynomial functions with real coefficients always come in conjugate pairs.
To find the remaining zero, we can use polynomial division or synthetic division to divide P(x) by (x - 1 - i)(x - 1 + i), which is the quadratic factor corresponding to the two known zeros:
2x^2 - 3x + 2
P(x) = --------------
(x - 1 - i)(x - 1 + i)
Now we need to solve for the roots of the quadratic factor 2x^2 - 3x + 2. We can use the quadratic formula:
x = [3 ± sqrt(9 - 4*2*2)] / (2*2)
= [3 ± sqrt(1)] / 4
= 1/2 or 2
Therefore, the remaining zeros of P(x) are 1/2 and 2. The three zeros of the polynomial function are 1 + i, 1 - i, 1/2, and 2.
Learn more about polynomial function here:https://brainly.com/question/2833285
#SPJ1
Solve for X. 8(x + 2) = 40 Simply your answer as much as possible. = x 6
Answers
Answer:
x = 3
Step-by-step explanation:
8(x+2) = 40
8x + 16 = 40
8x = 24
x = 3
Can anyone help solve this, please?

Answers
Answer:
7822.2222222
Step-by-step explanation:
4400 divied by 4.5% times 8=7822.22222222
Solve and check the following equations. Show your solution.
9.) 12 - 3x = 22 + 2x
10.) x + 7x - 12 = -20
11.) 7x + 4 - 13x = -1 + 23
Answers
Answer:
9. -2
10. -1
11. -3
Step-by-step explanation:
9. 12-3X=22+2X
Collect like terms
12-22=2X+3X
-10=5X
Divide both side by 5
X= -10/5 = -2
10. X+7X-12= -20
Collect like terms
X+7X = -20+12
8X= -8
Divide both side by 8
X= -8/8 = -1
11. 7X+4-13X= -1+23
Collect like terms
-7X-13X = -1+23-4
-6X = 18
Divide both side by -6
X= 18/-6 = -3
A company produces and sells solar panels for $520. The company's daily profit, P(x), can be modeled by the function P(x) = −6x2 + 156x + 1,000, where x is the number of $5 price increases for each solar panel. Use the graph to answer the questions. Graph of function p of x equals negative 6 x squared plus 156 x plus 1,000. The graph has the x-axis labeled as number of price increases, and the y-axis labeled as profit. The curve begins at (0, 1000), increases to the vertex at about (13, 2014), and decreases through about (31, 0). Part A: Identify the approximate value of the y-intercept. Explain what the y-intercept means in terms of the problem scenario. (3 points) Part B: Identify the approximate value of the x-intercept. Explain what the x-intercept means in terms of the problem scenario. (3 points) Part C: Identify the approximate value of the maximum of the function. Explain what the maximum of the function means in terms of the problem scenario. (4 points)
Answers
The maximum daily profit the company can earn is $2,350.
It is a set of points in a coordinate plane that represents the values of the function for different inputs.
The function P(x) = −6x² + 156x + 1,000 models the daily profit of the company, where x is the number of $5 price increases for each solar panel. The graph of the function has a vertex at approximately (15, 2350), which represents the maximum point on the graph.
Therefore, the maximum daily profit the company can earn is $2,350.
To know more about profit visit:
brainly.com/question/29959522
#SPJ1
At summer camp, 40 students are divided in two groups for swimming or hiking. Each camper flips a coin, where heads represents swimming and tails represents hiking. Outcome Frequency Swimming 16 Hiking 24 Compare the probabilities and determine which statement is true. The theoretical probability of swimming, P(swimming), is one half, but the experimental probability is 24 over 40. The theoretical probability of swimming, P(swimming), is one half, but the experimental probability is 16 over 40. The theoretical probability of swimming, P(swimming), is 16 over 24, but the experimental probability is one half. The theoretical probability of swimming, P(swimming), is 24 over 40, but the experimental probability is one half.
Answers
The correct statement is that the theoretical probability of swimming, P(swimming), is one half, but the experimental probability is 16 over 40.
We know that there are 40 students at summer camp who are divided into two groups for either swimming or hiking. Each camper flips a coin, where heads represents swimming and tails represents hiking. The outcome frequency for swimming is 16 and for hiking is 24.
To compare the probabilities, we need to first understand the difference between theoretical probability and experimental probability. Theoretical probability is the expected probability of an event occurring based on mathematical calculations and assumptions, whereas experimental probability is the actual observed probability of an event occurring based on data from experiments or observations.
Option 1 states that the theoretical probability of swimming is one half, but the experimental probability is 24 over 40. This statement is incorrect because the theoretical probability of swimming is actually 50%, which is equal to one half, and the experimental probability of swimming is also 40%, which is equal to 16 over 40. Therefore, this option is false.
Option 2 states that the theoretical probability of swimming is one half, but the experimental probability is 16 over 40. This statement is correct because the theoretical probability of swimming is 50%, which is equal to one half, and the experimental probability of swimming is also 40%, which is equal to 16 over 40. Therefore, this option is true.
Option 3 states that the theoretical probability of swimming is 16 over 24, but the experimental probability is one half. This statement is incorrect because the theoretical probability of swimming is actually 50%, which is not equal to 16 over 24, and the experimental probability of swimming is also 40%, which is not equal to one half. Therefore, this option is false.
Option 4 states that the theoretical probability of swimming is 24 over 40, but the experimental probability is one half. This statement is incorrect because the theoretical probability of swimming is actually 50%, which is not equal to 24 over 40, and the experimental probability of swimming is also 40%, which is not equal to one half. Therefore, this option is false.
In conclusion, the correct statement is that the theoretical probability of swimming, P(swimming), is one half, but the experimental probability is 16 over 40.
For more questions on experimental probability
https://brainly.com/question/26378307
#SPJ11