The thickness of 50 sheets of paper is 50mm. What is the thickness of each sheet in centimeters?
Answers
Hello!
50 sheets => 50mm
1 sheet => 50mm/50 = 1mm
1mm = 0.1cm
the answer is 0.1cm
Answer: 0.1
Step-by-step explanation:
1mm=0.1cm
So each sheet is 0.1cm
Related Questions
14 bags of candy for 36.26
Answers
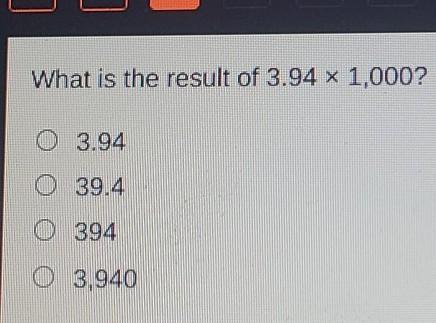
What is the result of 3.94 x 1,000? O 3.94 O 39.4 O 394 O 3,940
Answers
Answer:
3940 is the correct answer
Mrs. Brown has 11 more boys than girls in her class and has a total of 28 students. Which of the following systems of equations could be used to solve this problem?
A. B + 11 = G and B + G = 28
B. B = G – 11 and B + G = 28
C. G = B + 11 and B + G = 28
D. B = G + 11 and B + G = 28
Answers
B
B=G-11 and B+G=28 could be used to solve the problem
The line plots represent data collected on the travel times to school from two groups of 15 students.
A horizontal line starting at 0, with tick marks every two units up to 28. The line is labeled Minutes Traveled. There is one dot above 4,6,14, and 28. There are two dots above 10, 12, 18, and 22. There are three dots above 16. The graph is titled Bus 47 Travel Times.
A horizontal line starting at 0, with tick marks every two units up to 28. The line is labeled Minutes Traveled. There is one dot above 10,16,20, and 28. There are two dots above 8 and 14. There are three dots above18. There are four dots above 12. The graph is titled Bus 14 Travel Times.
Compare the data and use the correct measure of variability to determine which bus is the most consistent. Explain your answer.
Bus 47, with an IQR of 8
Bus 14, with an IQR of 6
Bus 47, with a range of 8
Bus 14, with a range of 6
Answers
\( \: \)
To determine which bus is the most consistent, we need to compare the interquartile ranges (IQR) and ranges of the two data sets.
Bus 47 has an IQR of 8 and a range of 8.
Bus 14 has an IQR of 6 and a range of 6.
The IQR is a better measure of variability than the range because it is less sensitive to outliers. In this case, we can see that Bus 14 has a smaller IQR, indicating that the travel times for Bus 14 are more consistent.
Therefore, Bus 14 is the most consistent bus in terms of travel times.
How much better or worse would it be to use the average nominal annual rate for two years with continuous compounding? Part III (40 Points) Suppose there are two banks in your town, Happy Bank and Trusty Bank Happy Bank is oşering semiannual compounding at a nominal annual rate of 604 percent. Trusty Bank is ofering monthly compounding at a nominal annual rate of 6.00 percent (In the questions that follow, it it is helpful, suppose the initial amount of money is $1000) 1. Which is a better deal if you are going to deposit money for three years? Explain your reasoning 2. Would your answer change if you were going to deposit money for nine years? Brieáy, why or why not? 3. Would your answer change if you were going to borrow money for three years? Brieáy, why or why not? 4. How long does it take for your money to triple at Trusty Bank?
Answers
2 If we were to deposit money for nine years, the answer may change as compounding frequency would have a greater effect over a longer time period.
3 The future value of a loan of $1000 would be $1,238.36, while at Trusty Bank it would be $1,169.81.
3 it takes approximately 11.55 years for the money to triple at Trusty Bank with monthly compounding.
When comparing the two banks, it is important to note that Happy Bank is offering semiannual compounding while Trusty Bank is offering monthly compounding. To compare the two rates on an equal basis, we need to convert them into their equivalent annual rates with continuous compounding, which takes into account compounding frequency.
The formula for the continuous compounding rate is e^(r/n)-1, where r is the nominal rate and n is the compounding frequency. For Happy Bank, the continuous compounding rate would be e^(0.06/2)-1 = 0.0294, or 2.94%. For Trusty Bank, the continuous compounding rate would be e^(0.06/12)-1 = 0.0049, or 0.49%.
Using these rates, we can calculate the future value of $1000 over three years. At Happy Bank, the future value would be $1,238.36, while at Trusty Bank it would be $1,169.81. Therefore, Happy Bank is the better deal for a three-year deposit.
If we were to deposit money for nine years, the answer may change as compounding frequency would have a greater effect over a longer time period. However, without additional information about compounding frequency and rates, we cannot determine which bank would be the better deal.
If we were to borrow money for three years, the calculations would be similar but the direction would be reversed. At Happy Bank, the future value of a loan of $1000 would be $1,238.36, while at Trusty Bank it would be $1,169.81. Therefore, Trusty Bank would be the better option for a three-year loan.
To determine how long it takes for the money to triple at Trusty Bank, we can use the formula FV = PV * e^(rt). If we start with $1000 and want to find when it will triple, we can set FV = $3000 and solve for t. This gives t = ln(3)/0.06 = 11.55 years. Therefore, it takes approximately 11.55 years for the money to triple at Trusty Bank with monthly compounding.
Learn more about Trusty here:
https://brainly.com/question/13372168
#SPJ11
Find the Difference quotient f(x+h)-f(x)/h, where h does not equal zero for the function below f(x)=x^2-5 Simplify the answer as much as possible Thank you
Answers
Main Answer:The difference quotient for the function f(x) = x^2 - 5 is 2x + h.
Supporting Question and Answer:
How do we calculate the difference quotient for a given function?
To calculate the difference quotient for a function, we need to evaluate the expression (f(x + h) - f(x)) / h, where f(x) represents the given function and h is a non-zero value.
Body of the Solution:To find the difference quotient for the function f(x) = x^2 - 5, we need to evaluate the expression (f(x + h) - f(x)) / h.
First, let's find f(x + h):
f(x + h) = (x + h)^2 - 5
= x^2 + 2hx + h^2 - 5.
Now, let's subtract f(x) from f(x + h):
f(x + h) - f(x) = (x^2 + 2hx + h^2 - 5) - (x^2 - 5)
= x^2 + 2hx + h^2 - 5 - x^2 + 5
= 2hx + h^2.
Finally, divide the result by h: (f(x + h) - f(x)) / h = (2hx + h^2) / h = 2x + h.
Final Answer: So, the simplified difference quotient for the function f(x) = x^2 - 5 is 2x + h.
To learn more about the difference quotient for a function from the given link
https://brainly.com/question/30427118
#SPJ4
The difference quotient for the function f(x) = x^2 - 5 is 2x + h.
How do we calculate the difference quotient for a given function?To calculate the difference quotient for a function, we need to evaluate the expression (f(x + h) - f(x)) / h, where f(x) represents the given function and h is a non-zero value.
To find the difference quotient for the function f(x) = x^2 - 5, we need to evaluate the expression (f(x + h) - f(x)) / h.
First, let's find f(x + h):
f(x + h) = (x + h)^2 - 5
= x^2 + 2hx + h^2 - 5.
Now, let's subtract f(x) from f(x + h):
f(x + h) - f(x) = (x^2 + 2hx + h^2 - 5) - (x^2 - 5)
= x^2 + 2hx + h^2 - 5 - x^2 + 5
= 2hx + h^2.
Finally, divide the result by h: (f(x + h) - f(x)) / h = (2hx + h^2) / h = 2x + h.
So, the simplified difference quotient for the function f(x) = x^2 - 5 is 2x + h.
To learn more about the difference quotient
brainly.com/question/30427118
#SPJ4
please please please NEED help ASAP I will mark 5 stars and brainliest if correct
|x-1| if x>1
**FULL EXPLANATION PLEASE FOR BRAINLIEST**
Answers
9514 1404 393
Answer:
x -1
Step-by-step explanation:
The absolute value function is piecewise linear. When its argument is negative, it gives the opposite of that argument:
|x| = -x . . . for x < 0
|x| = x . . . for x ≥ 0
__
When the argument is some function of x, the same rules apply.
|x -1| = -(x -1) . . . for (x -1) < 0
|x -1| = x -1 . . . for x -1 > 0
The condition x-1 > 0 is equivalent to x > 1, so you have ...
|x -1| = x -1 . . . for x > 1
_____
The attached graph shows that |x-1| and x-1 are the same graph when x>1.

Thank y’all for help
Answers
Answer:
Ask a question so I can answer it -_-Step-by-step explanation:
1. In the figure shown below, all angles are right angles,
and the side lengths given are in inches. What is the
area, in square inches, of the figure?
7
30
62
SKOG
2
120
Answers
Answer:iuygafsg78t arsy9u E)AFI_0=W]O-W[IOUPDIOYfguvydagai8sw09dQI
Step-by-step explanation:
A. Determine the distance between the ordered pairs given below. Round off your answers to the nearest hundredths.
1. (3, -2) and (7, 1)
2. (10, 13) and (2, 7)
3. (-5, -3) and (-9, -7)
4. (6, -11) and (-7, 2)
5. (-4, -5) and (8, 12)
Answers
Answer:
Step-by-step explanation:

In the US, among a representative group of 6,006 white men and 1,126 black men, ages 70-79 years at diagnosis of stage IV prostate cancer: 2,337 white men and 344 black men were alive after 5 years of follow-up. 1. Calculate the relative risk of being alive at 5-years after diagnosis associated between white men and black men (show formula and as much work as possible for partial credit)
Answers
The relative risk of being alive at 5-years after diagnosis associated between white men and black men is 2.03.
In the US, among a representative group of 6,006 white men and 1,126 black men, ages 70-79 years at diagnosis of stage IV prostate cancer: 2,337 white men and 344 black men were alive after 5 years of follow-up.
In order to calculate the relative risk of being alive at 5-years after diagnosis associated between white men and black men, we can use the following formula:
Relative risk = [ (number of white men alive after 5 years) / (total number of white men) ] ÷ [ (number of black men alive after 5 years) / (total number of black men) ]
Therefore, substituting the values given in the formula we get;
[ (2,337) / (6,006) ] ÷ [ (344) / (1,126) ] = 0.63 ÷ 0.31 = 2.03
Therefore, the relative risk of being alive at 5-years after diagnosis associated between white men and black men is 2.03.
learn more about relative risk here:
https://brainly.com/question/32288610
#SPJ11
#1: ZEGF and LBGC are vertical angles.
True
False

Answers
let f(x, y) be a function such that • the limit of f(x, y) as x → 0 along the path y = x is 0. • the limit of f(x, y) as x → 0 along the path y = x 2 is 0.
Answers
The function f(x, y) satisfies the conditions that its limit approaches zero as x approaches zero along two different paths: y = x and y = x^2. This implies that as x approaches zero, the function f(x, y) must approach zero regardless of whether y varies linearly or quadratically with x.
The given conditions state that the limit of f(x, y) as x approaches zero along the path y = x is zero. This means that as x gets arbitrarily close to zero, the function f(x, y) approaches zero when y varies linearly with x. Similarly, the second condition states that the limit of f(x, y) as x approaches zero along the path y = x^2 is also zero. This implies that when y varies quadratically with x, the function f(x, y) still approaches zero as x approaches zero. Therefore, the function f(x, y) must satisfy both conditions by converging to zero as x approaches zero along both paths.
To learn more about function click here: brainly.com/question/30721594
#SPJ11
Indicar a qué propiedad pertenece cada uno de los siguientes casos: -7,5 + 3/2 = -6 3√2 + 2√2 = 5√2 (1/2) + (3 + √8)
Answers
identify the equation for the line tangent to the circle x2 y2 = 169 at the point (−5, 12).
Answers
The equation for the line tangent to the circle \(\(x^2 + y^2 = 169\)\) at the point \(\((-5, 12)\)\) is \(\(x + 5y = 13\)\).
To find the equation of the tangent line to the circle at a given point, we need to determine the slope of the tangent line and its point of tangency. The slope of the tangent line is equal to the negative reciprocal of the derivative of the circle's equation with respect to x.
Differentiating the equation \(\(x^2 + y^2 = 169\)\) with respect to x, we get \(\(2x + 2y \frac{{dy}}{{dx}} = 0\)\). Rearranging this equation, we find \(\(\frac{{dy}}{{dx}} = -\frac{{x}}{{y}}\)\).
Substituting the coordinates of the given point (-5, 12) into the derivative, we have \(\(\frac{{dy}}{{dx}} = -\frac{{-5}}{{12}} = \frac{{5}}{{12}}\)\).
Since the tangent line has the same slope as the derivative at the point of tangency, the slope of the tangent line is \(\(\frac{{5}}{{12}}\)\).
Using the point-slope form of a line, \(\(y - y_1 = m(x - x_1)\)\), where \(\((x_1, y_1)\)\) is the given point, we substitute \(\((-5, 12)\)\) and the slope \(\(\frac{{5}}{{12}}\)\) to obtain \(\(y - 12 = \frac{{5}}{{12}}(x + 5)\)\).
Simplifying this equation, we get \(\(x + 5y = 13\)\), which is the equation of the tangent line to the circle at the point \(\((-5, 12)\)\).
To learn more about tangent refer:
https://brainly.com/question/30385886
#SPJ11
Write a recursive formula for the nth term of the sequence 5,12,19,26,....
Answers
Thus, beginning with a 1 = 5, the formula a n = a n-1 + 7 can be used to recursively find the nth term of the sequence.
what is sequence ?A sequence in mathematics is an ordered collection of numbers that is typically defined by a formula or rule. Every number in the series is referred to as a term, and its location within the sequence is referred to as its index. Depending on whether the list of terms stops or continues indefinitely, sequences can either be finite or infinite. By their patterns or uniformity, sequences can be categorised, and the study of sequences is crucial to many areas of mathematics, such as calculus, number theory, and combinatorics. Mathematical, geometrical, and Fibonacci sequences are a few examples of popular sequence types.
given
The sequence's terms are all different by 7 (i.e., 12 - 5 = 19 - 12 = 26 - 19 =... = 7).
The following is a definition of a recursive formula for the nth element of the sequence:
a 1 = 5 (the first term of the series is 5) (the first term of the sequence is 5)
For n > 1, each term is derived by adding 7 to the preceding term, so a n = a n-1 + 7.
Thus, beginning with a 1 = 5, the formula a n = a n-1 + 7 can be used to recursively find the nth term of the sequence. For instance, we have
a_2 = a_1 + 7 = 5 + 7 = 12
a_3 = a_2 + 7 = 12 + 7 = 19
a_4 = a_3 + 7 = 19 + 7 = 26
To know more about sequence visit:
https://brainly.com/question/21961097
#SPJ1
let f(x)=xe^-x^2 for all real numbers. find the value of xfxdx
Answers
The value of the integral ∫xf(x)dx is -(1/2)\(e^{-x^{2} }\) + C.
To find the value of the integral ∫xf(x)dx, we need to evaluate the definite integral using the given function f(x) = x\(e^{-x^{2} }\).
Let's proceed with the calculation:
∫xf(x)dx = ∫x(x\(e^{-x^{2} }\))dx
Using u-substitution, let:
u = -\(x^{2}\)
du = -2xdx
dx = -du / (2x)
Substituting the values:
∫x(x\(e^{-x^{2} }\))dx = ∫(x)(\(e^{u}\))(-du / (2x))
Simplifying:
∫(x\(e^{-x^{2} }\))dx = ∫(\(e^{u}\))(-du/2) = -(1/2) ∫\(e^{u}\)du
Integrating \(e^{u}\) with respect to u, we get:
∫\(e^{u}\)du = \(e^{u}\) + C
Substituting back for u:
∫(x\(e^{-x^{2} }\))dx = -(1/2) (\(e^{u}\) + C) = -(1/2)\(e^{-x^{2} }\) + C
Therefore, the value of the integral ∫xf(x)dx is:
-(1/2)\(e^{-x^{2} }\) + C, where C is the constant of integration.
To learn more about integral here:
https://brainly.com/question/29561411
#SPJ4
Triangle ABC is shown in the xy-coordinate plane. It will be rotates 90 degrees clockwise about the origin to form triangle A'B'C'. Graph the correct orientation of A'B'C' in the coordinate plane
Answers
For a 90 degrees clockwise rotation,
A' = (y, -x) = (1, -2)
B' = (y, -x) = (3, -3)
C' = (y, -x) = (2, -5)
How to graph a triangleTo plot a triangle onto a coordinate plane, these instructions must be followed:
Begin by drawing x and y axes to establish the necessary framework.
Choose three points upon which to place the vertices of the triangle on the graph.
Then connect the selected points through straight lines, thus resulting in the appearance of three sides; representing each point's distance from one another respectively.
Subsequently attach letter designations such as A, B, and C to each vertex.
Lastly, inspect the measurements of the sides and angles between them to confirm that they correspond with requisites specific to your chosen triangle type (such as an equilateral or Isosceles shape).
Read more about triangles here:
https://brainly.com/question/1058720
#SPJ1


Plot the direction field associated to the differential equation (16) u" + 192u = 0 together with the phase plot of the solution corresponding to the IVP (17) u" +192u = 0), 4(0) = 1/6, u'(0) = -1. using the exact solution (18) y(t) = = cos(8V31) – st=sin(8/3t). Determine R and 8 such that (19) y(t) = Rcos (8V3+ - 0) Plot the exact solution together with the estimated solution obtained via the tangent line method for step sizes h = 0.02,0.05,0.1 in the interval [0, 1].
Answers
We have to determine R and 8 such that(19) y(t) = Rcos (8V3t - 0) As we know, the solution of the given differential equation (1) is of the formu(t) = c1cos(8t√3) + c2sin(8t√3) Differentiating the given solution, we haveu'(t) = -8√3c1sin(8t√3) + 8√3c2cos(8t√3) Putting the initial conditions, we get 1/6 = c1
and -1 = -8√3c1 + 8√3c2On solving, we get
c1 = 1/6 and
c2 = 7/3√3
Therefore, the exact solution of the differential equation(1)\(u(t) = (1/6)cos(8t√3) + (7/3√3)sin(8t√3)\) The form of the solution of the differential equation (1) is \(y(t) = Rcos (8V3t - 0)\) Comparing the two equations, we get\(R = √(1/36 + 49/27) = 1/3√3 * √(4 + 49) = √53/9\) and 8 = tan^-1(7/3) Plot the exact solution together with the estimated solution obtained via the tangent line method for step sizes h = 0.02, 0.05, 0.1 in the interval [0, 1].Using the tangent line method, we have \(y(t+h) ≈ y(t) + h*y'(t)\) Therefore, the estimated solution obtained for h = 0.02,0.05,0.1 can be obtained by the following formulas:\(y(0.02) ≈ y(0) + 0.02*y'(0) y(0.05) ≈ y(0) + 0.05*y'(0)y(0.1) ≈ y(0) + 0.1*y'(0)\) Substituting the values of y(0) and y'(0), we get \(y(0.02) ≈ 1/6 - 0.02*8√3(7/3√3) ≈ -0.0701y(0.05) ≈ 1/6 - 0.05*8√3(7/3√3) ≈ -0.1461y(0.1) ≈ 1/6 - 0.1*8√3(7/3√3) ≈ -0.2893\) The estimated solutions are y(\(0.02) ≈ -0.0701y(0.05) ≈ -0.1461y(0.1) ≈ -0.2893\)
The exact solution and estimated solution obtained via the tangent line method for step sizes h = 0.02,0.05,0.1 in the interval [0, 1]
To know more about Tangent visit-
https://brainly.com/question/10053881
#SPJ11
Add. Write your answer in simplest form.
G
1
3
x + 3 +
9) =
-x-9
Need help with this question?
Answers
The answer in simplest form is x = -3/4
What is an equation?
In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign =
The given equation is
3x + 3 +9 =-x-9
Collecting like terms to have
3x + x = -9+9-3
4x = -3
Making x the subject of the relation
Therefore, the value of x is x = -3/4
Learn more about equations on https://brainly.com/question/29657992
#SPJ1
Find a set of columns that form a basis for the column space of each of the following matrices. Give the rank of each matrix. Also find a basis for the null space of each matrix. [ -3 6 5 -10] [ 2 1 1 1 2 1 7 5 4] [ 1 1 0 0 1 1 0 0 1 1 0 1 1 0 1 0 0 1 1 1 1 1 0 0 1] [ 1 1 1 0 1 0 1 0 1 0 2 1 2 -1 2 -1 1 -1 2 -1 1 2 1 1 1]
Answers
We can use row reduction to solve this system of equations:
[1 1 0 0 1; 1 1 1 0 0; 1 0 1 1 0; 0 0 1 1 1; 1 1 1 1 1] => [1 0 0 -1 0; 0 1 0 1 0; 0 0 1 1 0;
For the matrix [ -3 6 5 -10], we can see that there are two linearly independent columns, namely [-3 2 1] and [6 1 1]. Therefore, a basis for the column space of this matrix is {[ -3 2 1], [6 1 1]}. The rank of this matrix is 2.
To find a basis for the null space of this matrix, we solve the equation Ax = 0, where A is the given matrix:
[ -3 6 5 -10] [x1] [0]
[x2] = [0]
[x3]
[x4]
This simplifies to:
-3x1 + 6x2 + 5x3 - 10x4 = 0
We can rewrite this equation as:
x1 = 2x2 - (5/3)x3 + (10/3)x4
Therefore, the null space of this matrix is spanned by the vector [2, 1, 0, 0], [ -5/3, 0, 1, 0], and [10/3, 0, 0, 1].
For the matrix [2 1 1; 1 2 1; 7 5 4], we can see that all three columns are linearly independent. Therefore, a basis for the column space of this matrix is {[2 1 7], [1 2 5], [1 1 4]}. The rank of this matrix is 3.
To find a basis for the null space of this matrix, we solve the equation Ax = 0, where A is the given matrix:
[2 1 1; 1 2 1; 7 5 4] [x1] [0]
[x2] = [0]
[x3]
This simplifies to:
2x1 + x2 + x3 = 0
x1 + 2x2 + 5x3 = 0
x1 + x2 + 4x3 = 0
We can use row reduction to solve this system of equations:
[2 1 1; 1 2 1; 7 5 4] => [1/2 1/4 -1/4; 0 9/4 -1/4; 0 0 0]
The reduced row echelon form shows that the null space of this matrix is spanned by the vector [-1/2, 1/2, 1], and [1/4, -1/4, 1].
For the matrix [1 1 0 0 1; 1 1 1 0 0; 1 0 1 1 0; 0 0 1 1 1; 1 1 1 1 1], we can see that all five columns are linearly independent. Therefore, a basis for the column space of this matrix is {[1 1 1 0 1], [1 1 0 0 1], [0 1 1 1 1], [0 0 1 1 1], [1 0 0 1 1]}. The rank of this matrix is 5.
To find a basis for the null space of this matrix, we solve the equation Ax = 0, where A is the given matrix:
[1 1 0 0 1; 1 1 1 0 0; 1 0 1 1 0; 0 0 1 1 1; 1 1 1 1 1] [x1] [0]
[x2] = [0]
[x3]
[x4]
[x5]
This simplifies to:
x1 + x2 + x5 = 0
x1 + x2 + x3 = 0
x1 + x3 + x4 = 0
x4 + x5 = 0
x1 + x2 + x3 + x4 + x5 = 0
We can use row reduction to solve this system of equations:
[1 1 0 0 1; 1 1 1 0 0; 1 0 1 1 0; 0 0 1 1 1; 1 1 1 1 1] => [1 0 0 -1 0; 0 1 0 1 0; 0 0 1 1 0;
Learn more about matrix here:
https://brainly.com/question/29132693
#SPJ11
What is the highest common factor of 16a + 24b
Answers
The highest common factor of 16a + 24b is 2a + 3b by finding out the greatest common factor.
To find the highest common factor of 16a + 24b, we need to determine the greatest common factor of its terms, which are 16 and 24.
First, we can factor out the greatest common factor of the coefficients, which is 8:
16a + 24b = 8(2a + 3b)
Now, we can see that 2a + 3b is the highest common factor of 16a + 24b, because it is the largest expression that divides both terms evenly.
The highest common factor is also known as the greatest common divisor or greatest common factor, and it is often used in solving equations, simplifying fractions, and finding common denominators.
To learn more about factor click on,
https://brainly.com/question/10565675
#SPJ4
You and your family are driving to the Wild Animal Park in Escondido, CA. The distance from your house to the park is 528 miles. You hope to get there in 8 hours of driving time. What would be your average driving speed. Explain your thinking
Answers
Answer:
66 m/h
average speed = distance / time
528/8 = 66m/h
Step-by-step explanation:
write the ratio 4 : 3/6 in terms of 1 : n
Answers
Answer:
1:1/8
Step-by-step explanation:
we can see that 4 went down to 1, it must have been divided by 4 therefore we also ivide 3/6 by 4 which gives us the answer
4. Find the value of x.
A 7
B -7
C 3
D 3.5

Answers
Answer:
l got 7 sorry if it is not the answer
Step-by-step explanation:
2x+12=5x-9 two will come to the other side n become 5x-2x=3x then 9 will go to the other side n become 12+9=21
3x=21 then divide both sides by 3
Four hundred draws will be made at random with replacement from the box |[1][3][5][7]| (a) Estimate the chance that the sum of the draws will be more than1,500. (b) Estimate the chance that there will be fewer than 90 [3] 's.
Answers
(a) The chance that the sum of the draws will be more than 1,500
(b) The chance that there will be fewer than 90 occurrences of the number 3.
(a) To estimate the chance that the sum of the draws will be more than 1,500, we need to consider the possible combinations and their probabilities. Since there are four numbers in the box, each with an equal chance of being drawn, we can calculate the mean and standard deviation of the draws. With this information, we can use statistical methods such as the normal distribution to estimate the probability of the sum exceeding 1,500.
(b) To estimate the chance that there will be fewer than 90 occurrences of the number 3, we need to calculate the probability of drawing a 3 in each individual draw and then consider the distribution of the number of 3's over the 400 draws. Using statistical techniques such as the binomial distribution, we can estimate the probability of having fewer than 90 occurrences of 3 in the 400 draws.
Both estimations involve applying statistical methods to analyze the probabilities of specific events occurring in the random drawing process. The precise calculations and estimations would require detailed information about the probabilities of drawing each number and the distribution of these numbers in the box.
Learn more about binomial distribution here:
https://brainly.com/question/29163389
#SPj11
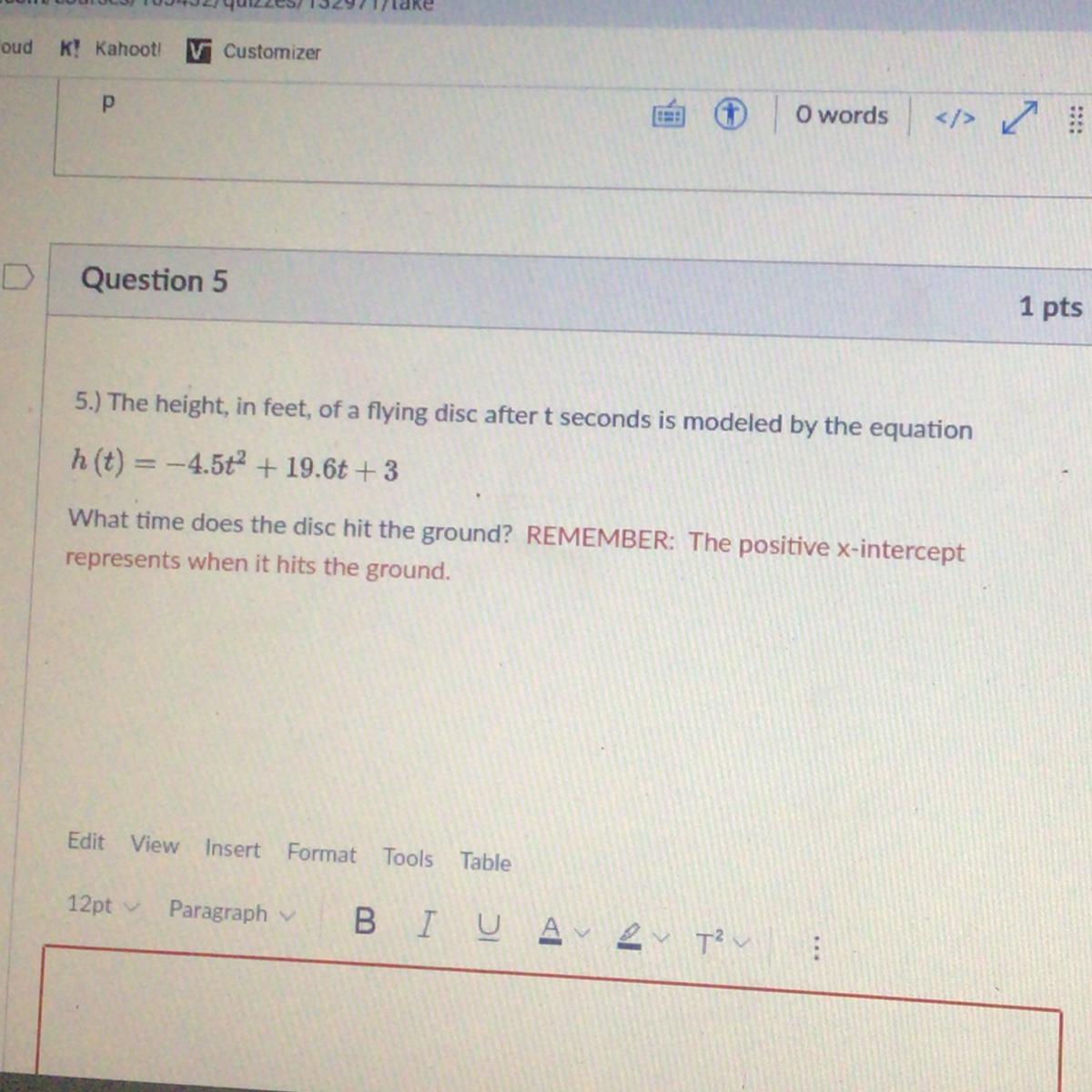
WILL BRAINLIST IF RIGHT (20points)
Answers
Answer:
-24.1t^2+3
Step-by-step explanation:
A fair die is rolled times. What is the probability that a is obtained on at least one of the rolls
Answers
the probability of rolling a 1 on at least one of the rolls of a fair die is 1 - (5/6)^n.
To find the probability of rolling a 1 on at least one of the rolls of a fair die, we can use the concept of complementary probability.
The complementary probability is the probability of the opposite event, which in this case is the probability of not rolling a 1 on any of the rolls.
The probability of not rolling a 1 on a single roll of a fair die is 5/6, since there are 5 possible outcomes (2, 3, 4, 5, 6) out of 6 total outcomes.
Therefore, the probability of not rolling a 1 on all n rolls is (5/6)^n.
The probability of rolling a 1 on at least one of the rolls is equal to 1 minus the probability of not rolling a 1 on any of the rolls:
P(rolling a 1 on at least one roll) = 1 - P(not rolling a 1 on any roll)
P(rolling a 1 on at least one roll) = 1 - (5/6)^n
To know more about probability visit:
brainly.com/question/31828911
#SPJ11
46/21 as a decimal rounded to the nearest tenth
Answers
Answer:
2.2
Step-by-step explanation:
46/21 rounded to nearest tenth place is zero.
What is rounding of nos. ?Rounding nos. to nearest places have an advantage that is we could remember the number easily.
For example - 16534 rounded to ten thousand's place is 20000 which is more easier for us to remember and also the number rounded to a certain place retains it's value to about that place.
According to the given question we have to convert the fraction 46/21 as a decimal rounded to the nearest tenth.
We know,
46/21 is
= 2.2 approximately .
Now, if we round 2.2 to the nearest tenth, 2.2 can be written as 02.2.
We observe that it's tenth digit is 0 so when we round it to the nearest tenth place it will be 0.
learn more about rounding of numbers here :
https://brainly.com/question/27734142
#SPJ2
helpppppp i need help with this

Answers
Answer:
B=54
C=54
Step-by-step explanation:
180-72=108
108/2=54
54*2=108
108+72=180