The table and the graph below each show a different relationship between the same two variables, x and y:
How much more would the value of y be on the graph than its value in the table when x = 12?
A. 20
B. 30
C. 60
D. 70

Answers
The value of y will be 60 so the correct answer is option C.
What is a graph?A graph is the representation of the data on the vertical and horizontal coordinates so we can see the trend of the data.
There is a linear relationship between the two variables x and y. For the given data in the table as well as in the graph. The expression for the two variables will be written in the form of an equation as follows:-
The expression for the data in the table:-
y = 25 x now at x = 12
y = 25 x 12 = 300
The expression for the values in the graph:-
y = 30x at x = 12
y = 30 x 12
Y = 360
How much more would the value of y be on the graph will be calculated as:-
Value = 360 - 300
Value = 60
Therefore the value of y will be 60 so the correct answer is option C.
To know more about graphs follow
https://brainly.com/question/25020119
#SPJ1
Related Questions
K
The voltage V of an audio speaker can be represented by V=2√P, where P is the power of the speaker. An engineer wants to design a speaker with 576 watts of power. What will
the voltage be?
volts
Answers
According to the given voltage function, the value of the voltage for the power of 576 watts is 48 watts.
Function:
The relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output.
Given,
The voltage V of an audio speaker can be represented by V=2√P, where P is the power of the speaker. An engineer wants to design a speaker with 576 watts of power.
Here we need to find the voltage of the given power.
In the given question we have the voltage function
v = 2√P
Where P refer the power of the speaker.
Here we have to find the voltage if engineer wants to design a speaker with 576 watts of power.
Which means the value of P is 576.
Then the value of V is calculated as,
v = 2 √576
We know that the value of √576 = 24,
So,
v = 2 x 24
v = 48.
Therefore, the voltage is 48 watts.
To know more about Function here.
https://brainly.com/question/28303908
#SPJ1
Evaluate the integral: S18 1 (√3/z)dz
Answers
The value of the integral is ln(1/6) + (3/2) ln(3). To evaluate the integral S18 1 (√3/z)dz, we can use the substitution u = √3/z, which implies du/dz = (-√3/z²) and dz = (-z²/√3) du.
Substituting u = √3/z and dz = (-z²/√3) du, the integral becomes:
S18 1 (√3/z)dz = -S√3/18 ∞ √3/1 u du
= -S√3/18 ∞ √3/1 (√3/u) du
= -S1 18 (3/u) du
= -3ln(u) |1 18
= -3ln(18/√3) + 3ln(1/√3)
= -3ln(6) + 3ln(√3)
= -3ln(6) + 3/2 ln(3)
= ln(1/6) + (3/2) ln(3)
Therefore, the value of the integral is ln(1/6) + (3/2) ln(3).
Learn more about “ evaluate the integral “ visit here;
https://brainly.com/question/31585464
#SPJ4
gtbbbbbbnweij etrbintriubnrtgiubjntiubntriubidjfbfjdbdfbgfgbfgfdbenriub ugnbsssssssssssssssssssssssssssssssssssssssssssssssssssssyjvhfghregfhjvfdbgbgvbgb

Answers
Answer:
No solutions is your answer
Step-by-step explanation:
I hope it helps and don't give up just like it says in i ready
liz has two children. the taller child is a boy. what is the probability that the other child is a boy? assume that in 76% of families consisting of one son and one daughter the son is taller than the daughter.
Answers
The probability that Liz has two boys given that she has at least one boy who is taller is approximately 0.2841
Let's first consider all possible gender combinations of Liz's two children:
Boy, boy (BB)
Boy, girl (BG)
Girl, boy (GB)
Girl, girl (GG)
We know that Liz has at least one boy, which rules out the GG combination. That leaves us with three possible combinations: BB, BG, and GB.
From the given information, we know that in 76% of families consisting of one son and one daughter, the son is taller than the daughter. This means that in the BB combination, the probability that the taller child is a boy is 1 (since both children are boys), and in the BG and GB combinations, the probability is 0.76 (since there is one boy and one girl, and we know the boy is taller).
So, let's calculate the probability that Liz has two boys (BB) given that she has at least one boy who is taller. We can use Bayes' theorem for this
P(BB | taller child is a boy) = P(taller child is a boy | BB) × P(BB) / P(taller child is a boy)
where P(taller child is a boy | BB) = 1 (as both children are boys), P(BB) = 1/4 (since there are four possible gender combinations), and P(taller child is a boy) = P(taller child is a boy | BB) × P(BB) + P(taller child is a boy | BG) × P(BG) + P(taller child is a boy | GB) × P(GB) = 1 × 1/4 + 0.76 × 1/2 + 0.76 × 1/2 = 0.88.
Substituting these values into Bayes' theorem, we get
P(BB | taller child is a boy) = 1 × 1/4 / 0.88 = 0.2841
Learn more about probability here
brainly.com/question/11234923
#SPJ4
Solve for x by factorising.
3x²+4x= 4
Answers
Answer:
Step-by-step explanation:
3x^2+4x-4=0 (we move 4 to the other side to factor)
(3x-2)(x+2)
^think of 2 numbers that when you multiply it will be -4 and when you multiply one of it to 3x and add to the other it will be 4x.
Recheck:
-2(2)= -4 (correct)
-2x+6x=4x (correct)
the 5th term of an arithmetic progression is three times the first term. find the sum of the first eight terms of the progression given that quarter of the fifth term is 9.
Answers
Answer:
Let the first term be "a" and common difference be "d". Then, the fifth term is 3a.
Quarter of the fifth term is 9, so (1/4) * 3a = 9. Solving for a, we get:
a = 36.The sum of the first 8 terms of an arithmetic progression can be found using the formula:
S_n = n/2 * (2a + (n - 1)d)
where n is the number of terms.In this case, n = 8, so:
S_8 = 8/2 * (2 * 36 + (8 - 1) * d)
= 4 * (72 + 7d)
= 288 + 28dSince the common difference is "d", the sum of the first eight terms is 288 + 28d.
Correct me if I’m wrong
The sum of the first eight terms of the arithmetic progression is 264.
What is an arithmetic sequence?An arithmetic sequence is a set of numbers where each phrase is created by multiplying the previous term by a constant amount (referred to as the common difference). In other terms, an arithmetic sequence is a set of numbers that changes in value from one term to the next by a fixed amount.
Let the first term of the arithmetic progression be represented by 'a', and let the common difference between terms be represented by 'd'.
Then, according to the problem statement, we know that the fifth term is three times the first term, so:
a + 4d = 3a
Simplifying this equation, we get:
2a = 4d
a = 2d
Now we can use the fact that a quarter of the fifth term is 9 to solve for d:
(1/4)(3a) = 9
3a = 36
a = 12
d = a/2 = 6
So the arithmetic progression is: 12, 18, 24, 30, 36, 42, 48, 54
The sum of the first eight terms can be found using the formula:
S₈ = (n/2)(2a + (n-1)d)
where n = 8 is the number of terms.
Plugging in the values we have found, we get:
S₈ = (8/2)(2(12) + (8-1)(6))
S₈ = 4(24 + 42)
S₈ = 4(66)
S₈ = 264
Therefore, the sum of the first eight terms of the arithmetic progression is 264.
To know more about arithmetic sequences follow
https://brainly.com/question/29179881
#SPJ2
PLEASE HELP ME OUT 12x^2+4x-1
Answers
(if im wrong then mb)
Answer:
(6x-1)(2x+1)
Step-by-step explanation:
12x²+4x-1 (find two numbers that when you add or subtract them the ANS will be the coefficient of x and those same numbers when you multiply them the ANS will be the product of 12 and -1) then replace the middle term with those numbers.
12x²+6x-2x-1
(12x²+6x)(-2x-1)
6x(2x+1)-1(2x+1)
(6x-1)(2x+1)
how do I solve this .... question in the image.
thank you

Answers
Answer:
Below
Step-by-step explanation:
● x-20 = y+20 (1)
● 2(y-22) = x+22 (2)
This is a system of simulataneous equations
Let's simplify the expressions first
● x -20 = y + 20 (1)
Add 20 to both sides
● x -20 + 20 = y+20 +20
● x = y + 40 (1)
● 2(y-22) = x+22 (2)
● 2y - 44 = x +22
Substrat 22 from both sides
● 2y-44-22 = x+22-22
● 2y -66 = x (2)
This is the new system:
● x = y+40 (1)
● x = 2y-66 (2)
Substract (2) from (1)
● x-x = y+40-(2y-66)
● y+40-2y+66 = 0
● -y +106 = 0
● y = 106
Replace y with 106 in (1)
● x = y +40
● x = 106+40
● x = 146
So the solutions are (146,106)
if ab is dilated by a scale factor of 2 centered at (3,5), what are the coordinates of the endpoints of its image, a9b9 ? (1) a9(27,5) and b9(9,1) (3) a9(26,8) and b9(10,4) (2) a9(21,6) and b9(7,4) (4) a9(29,3) and b9(7,21)
Answers
To find the coordinates of the endpoints of the image A'B' (A9B9) after dilation of AB by a scale factor of 2 centered at (3,5), follow these steps:
Step 1: Use the given scale factor (2) and center of dilation (3,5).
Step 2: Apply the dilation formula to the coordinates of the original points A and B. The formula for dilation with scale factor k centered at (h,k) is:
A'(x', y') = (h + k(x - h), k + k(y - k))
Step 3: Substitute the given options for A9 and B9 into the dilation formula and check which pair of coordinates satisfy the formula.
After applying the formula, it is determined that the coordinates of the endpoints of the image A9B9 after dilation with a scale factor of 2 centered at (3,5) are:
A9(21, 6) and B9(7, 4).
Option (2) is correct.
Learn more about coordinates :
https://brainly.com/question/12617743
#SPJ11
Hello! Having a little trouble on this question, thanks for your help!




Answers
The graph of the function:
\(g(x)=ln(4-x)\)Can be obtained by using the parent function:
\(f(x)=ln(x)\)Whose graph is shown below:
We must first turn x into -x by making a reflection over the y-axis. This way, the function becomes:
\(f(-x)=ln(-x)\)And the graph is:
Finally, we just add 4 to x to translate the graph 4 units to the right to get our desired function:
\(g(x)=f(4-x)=ln(4-x)\)The graph is shifted 4 units to the right as shown:



Choose the best answer.
A statement in which a conclusion is true if the conditions of a particular hypothesis are true is called a
Answers
A statement in which a conclusion is true if the conditions of a particular hypothesis are true is called a conditional statement.
What is the conditional statement?A conditional statement is one that has the form "If P then Q," where P and Q are sentences. P is referred to as the hypothesis in this conditional statement, and Q is referred to as the conclusion. "If P then Q" implies that Q must be true sometimes when P is true.
The type of conditional statements are as follows:
General truth: I feel better all day if I eat breakfast.Future event - I will investigate tonight if I have a scan tomorrow.Assumption: If I had a million dollars, I would purchase an airplane!Hypothetical outcome - I might have been offered the position if I had geared up for the interview.A statement in which a conclusion is true if the conditions of a particular hypothesis are true is called a conditional statement.
More about the conditional statement link is given below.
https://brainly.com/question/18152035
#SPJ1
HELPPP HELPP!! WHAT IS THE VALUE OF X AND W???

Answers
Answer:
w = 42
x = 29
Step-by-step explanation:
We know that w + 138 must equal 180, so we get 42 for w. Then we know that 19 + x + 2 = 90, and w = 42. So if we add 42 + 19, and subtract that from 90, we get 29. Hope this helps!
Determine the power and the rms value for each of the following signals:
a) 5 + 10cos(10t + π/3)
b) 10cos(100t + π/3) + 16 sin(150t + π/5)
c) (10 + 2 sin (3t)) cos 10t
d) 10 cos(5t)cos(10t)
e) 10 sin(5t)cos(10t)
f) e^(jαt) cos(w0t)
Answers
The power and the r m s value for each of the following signals are a)p=50w and r m s =7.07 b)p=178w, r m s =√178 c)p=51w, r m s =√51
d)p=25w, r m s =√25 e)p=25w, r m s =√25 and f)p=1/2, r m s =√1/2.
(a) 5+10cos(100t+π/3)
=A cos(w0t+θ)
power of the signal
P=10^ 2/2=100/2=50w
p=50w
r m s value of the signal
=√50
=7.07
b) 10cos(100t+π/3)+16sin(150t+π/5)
power of the signal.
p=10^ 2/2+16^ 2/2
p=178w
r m s value of the signal=√178
c) (10+2sin(3t)cos10t
=10cos10t+2sin3tcos210t
=2sin3tcos10t
=1/2(sin(3+10)+sin(3-10))
(sin a cos b=1/2(sin(a + b)+sin(a-b))
=2x1/2(sin13t-sin7t)
=sin13t-sin7t
=10cos10t+sin13t-sin7t
power of the signal is
p=10^ 2/2+1^ 2/2+1^ 2/2
p=51w
r m s value of the signal=√51
d) 10 cos(5t)cos(10t)
=10(cos(5+10)T+ cos (5-10)t/2
(cos a cos b=1/2(cos a+ cos b)+cos(a-b))
=10(cos(15)t+ cos (-5)t/2
=5cos15t-5cost
power value of the signal
p=5^ 2/2+5^ 2/2
p=25w
r m s value of the signal=√25
e) 10 sin(5t)cos(10t)
=10(sin(5+10)t+ sin(5-10)t/2
=10/2(sin15t-sin5t)
=5sin15t-5sin5t
power of the signal
p=5^ 2/2+5^ 2/2
p=25w
r m s value of the =√25
F) f) e^(jαt) cos(w0t)
=e jαt cos wot
=(cosαt+ cos wot+jsin2tcoswot
=(cos(α+wo)t+ cos(α-wo)t/2+j(sin(2+wo)t+ sin cos-wot/2
=1/2cos(α+wo)T+1/2cos(α-wo)T
power of the signal
p=(1/2)^ 2/2+(1/2)^ 2/2+(1/2)^ 2/2+(1/2)^ 2/2
p=1/2
r m s value=√1/2
To learn more about power and the r m s values.
https://brainly.com/question/29481359
#SPJ4
\(\pi\)
An urn holds 9 identical balls except that 1 is white, 3 are black, and 5 are red. An exp How many outcomes are in the sample space for this experiment? How many outcomes are in the event "no ball is
Answers
Answer c
Step-by-step explanation:
CAN SOMEONE HELP ME I WILL GIVE BRAINLIEST TO THE ONE WITH THE RIGHT ANSWER!!!
In a small city, approximately 15% of those eligible are called for jury duty in any one calendar year. People are selected for jury duty at random from those eligible, and the same individual cannot be called more than once in the same year. What is the probability that a particular eligible person in this city is selected two years in a row? three years in a row?
Answers
Answer:
Two years in a row: 2.25%
Three years in a row: 0.3375%
Step-by-step explanation:
For two years in a row:
15/100*15/100
225/10000=
0.0225
0.0225*100 (for percentage)= 2.25%
For three years in a row:
15/100*15/100*15/100
3375/1000000=
0.003375
0.003375*100 (for percentage)=0.3375%
the world population in 1997 was 5.88billion. the world population in 2017was 7.53billion. assume that the ratio between the population in two consecutive years was constant between 1997 and 2017. which equation can be used to find r,the rate of growth per year of the world population?
Answers
The equation that can be used to find r, the rate of growth per year of the world population, is \(r = (7.53 / 5.88 )^{(1/20)} - 1\).
If we assume that the growth rate of the world population was constant from 1997 to 2017, then we can use the following equation:
Population in 2017 = Population in 1997 × (1 + r)²⁰
where r is the annual growth rate, and the exponent 20 represents the number of years between 1997 and 2017.
We can rewrite this equation to solve for r:
(7.53 ) = (5.88 ) × (1 + r)²⁰
Divide both sides by (5.88 ):
(7.53 ) / (5.88 ) = (1 + r)²⁰
Take the 20th root of both sides:
\((7.53 / 5.88 )^{(1/20)} = 1 + r\)
Subtract 1 from both sides:
\(r = (7.53 / 5.88 )^{(1/20)} - 1\)
Therefore, the equation that can be used to find r, the rate of growth per year of the world population, is \(r = (7.53 / 5.88 )^{(1/20)} - 1\).
Learn more about the growth rate here:
https://brainly.com/question/29291084
#SPJ1
Find the area of the region bounded by \[ y=\frac{7}{(4+x)^{2}}+\frac{5}{7+x^{2}}, \quad y=0, x \geq 5 . \]
Answers
The area of the region bounded by
\[y=\frac{7}{(4+x)^2}+\frac{5}{7+x^2},\ y=0,\ x\ge5\]is 0.0188 (rounded to four decimal places).
Here's how to get the solution:
We are asked to find the area of the region bounded by the two curves.
The curves intersect at (5, 0) because x can not be less than 5.
They meet again at the point x ≈ 1.281.
Now, we must find the integrals for both functions in the given range.
We'll call the first function "f (x)" and the second "g (x)."
f(x) = 7 / (4 + x)² + 5 / (7 + x²)
g(x) = 0
The area between the two curves is obtained by finding the integral of the difference of the two functions.
The area is given by:
\[\int_{5}^{1.281} [f(x) - g(x)] dx\]
Since there is no point of intersection beyond x ≈ 1.281, we will use this value for the limit of integration.
Integrating:
\[\begin{aligned} &\int_{5}^{1.281} [f(x) - g(x)] dx \\ =& \int_{5}^{1.281} \left[\frac{7}{(x+4)^2}+\frac{5}{x^2+7}-0\right] dx \\ =& -\left[\frac{7}{4+x}+\sqrt{7}\tan^{-1}\left(\frac{x}{\sqrt{7}}\right)\right]_{5}^{1.281} \\ =& 0.0188. \end{aligned}\]
Thus, the area of the region is 0.0188.
Learn more about "calculating area by integration":
brainly.com/question/30452445
#SPJ11
Trevor is walking to school from home. He leaves and travels 58.0m before he forgets his lunch. He turns around, goes back home and grabs his lunch. He then walks 236m before he gets to school.
What is the total distance Trevor travelled? Round to three significant digits., do not include units.
Answers
The total distance Trevor traveled is 352 meters.
We have,
Trevor is traveling from his home to school.
He first walks 58.0 meters in one direction, but then he forgets his lunch and has to turn around and walk back the same distance.
This means he has walked a total distance of 58.0 m + 58.0 m = 116.0 m.
Now,
After he retrieves his lunch, he continues walking in the original direction for an additional 236 meters.
So, the total distance Trevor traveled.
= 116.0 m + 236 m = 352.0 m.
Thus,
The total distance Trevor traveled is 352 meters.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
Solve the equation showing all work.
X²-4x+3=0
Answers
x2−4x+3=0
For this equation: a=1, b=-4, c=3
1x2+−4x+3=0
Step 1: Use quadratic formula with a=1, b=-4, c=3.
x=
−b±√b2−4ac
2a
x=
−(−4)±√(−4)2−4(1)(3)
2(1)
x=
4±√4
2
x=3 or x=1
Answer:
x = 1, x = 3
Step-by-step explanation:
x² - 4x + 3 = 0
consider the factors of the constant term (+ 3) which sum to give the coefficient of the x- term (- 4)
the factors are - 1 and - 3 , since
- 1 × - 3 = + 3 and - 1 - 3 = - 4 , then
(x - 1)(x - 3) = 0 ← in factored form
equate each factor to zero and solve for x
x - 1 = 0 ⇒ x = 1
x - 3 = 0 ⇒ x = 3
Suppose that P(A)=3/5 and P(B)=2/3. Then
A. P (AUB) < 2/3
B. 4/15 < P (AnB) < 3/5
C. 2/5 < P(A|B) < 9/10
D. P (AnB) < 1/3
Answers
Suppose that probability P(A)=3/5 and P(B)=2/3 then the correct answers are option B , C, D that is 4/15 < P (AnB) < 3/5, 2/5 < P(A|B) < 9/10 and . P (AnB) < 1/3.
Events that are mutually exclusive do not occur at the same time. For example, when a coin is tossed, the outcome will be either head or tail, but we cannot obtain both. Such occurrences are also known as disjunct events since they do not occur at the same time. If A and B are mutually exclusive occurrences, the probability of each is given by P(A Or B) or P(A Or B) (A U B).
Maximum of P(A∪B) can be 1.
Maximum of P(A∩B) is minimum of A and B, hence, 3/5.
Minimum of P(A∩B) is when the union of A and B is 1. Thus, P(A∩B) = 2/3+3/5−1=4/15
Thus, P(A∣B)=P(A∩B)/P(B) will range from,
9/10 to 2/5.
Maximum of P(A∩B ′ ) is maximum when there is minimum intersection,
hence P(A∩B ′ )=P(A)−P(A∩B) = 1/3
Two occurrences are said to be mutually exclusive in probability theory if they cannot occur at the same time or concurrently. In other words, discontinuous events are those that are mutually exclusive. If two occurrences are regarded discontinuous, the likelihood of both happening at the same time is zero.
Learn more about Probability:
https://brainly.com/question/11781228
#SPJ4
Solve the equation using the distributive property and properties of equality.
2(x-8) = 68
What is the value of x?
26
30
ОООО
38
42
Answers
(WORK SHOWN BELOW)

ANSWER ASAP ILL MARK BRAINLIEST!!!!
find all the real zeros of the quadratic function.
f(x)=2x²-6x-1
Answers
Answer:
\(2 {x}^{2} - 6x - 1 = 0 \\ a = 2 \: \: \: b = - 6 \: \: \: c = - 1 \\ \\ x = \frac{6\binom{ + }{ - } \ \sqrt{ {6}^{2} - 4(2)( - 1)} }{2 \times 2} \\ \\ x = \frac{6 \binom{ + }{ - } \sqrt{44} }{4} \\ x = \frac{6 + \sqrt{44} }{4} \\ \\ or x = \frac{6 - \sqrt{44} }{4} \)
I hope that is useful for you :)
who knows the answer

Answers
Answer: 6 gallons
Step-by-step explanation:
4/30 * 45 = 6
Multiply. Write each product in simplest form.
9. 3×11
10. //
13. 021-
12.
20
=
=
=
11. 2×4=
8 9
X
18 20
14.
=
Answers
Answer:
Te conozco y sé qué
Como Nuevo de fabrica el otro
Find the equation of the line shown.
y
10
NWAUTO
7
6
5
4
3
2
х
O
1 2 3 4 5 6 7 8 9 10
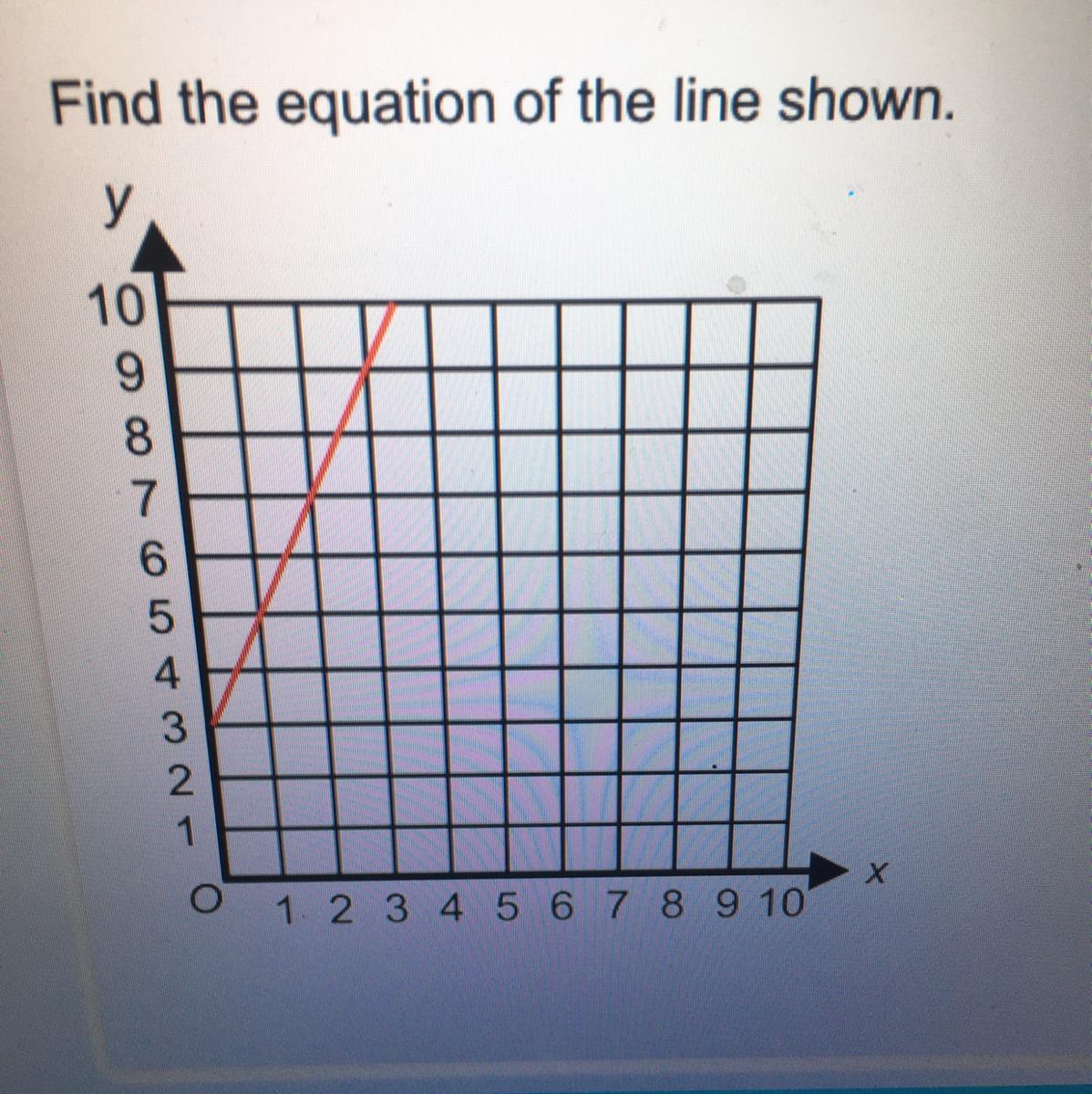
Answers
Answer:
The equation of the line is: y=2x + 3
Find the value of x. Round to the nearest tenth. Use law of sines

Answers
Answer:
69.9°
Step-by-step explanation:
sin28/11 = sinx/22
22(sin28) = 11(sinx)
sinx = 22(sin28) / 11 = 0.9389
x = sin⁻¹(0.9389) = 69.9°
Can any one help with me please

Answers
Answer:
85
Step-by-step explanation:
The vertical line that y is on adds up to 180 so if we take 180 - the number we already know (95) we get 85
Which line models the data points better and why? (1 point) Oblue, because it is longer Oblue, because the data points are all close to the line Ored, because it goes through one of the points Ored, because there are three points above the line and three points below the line
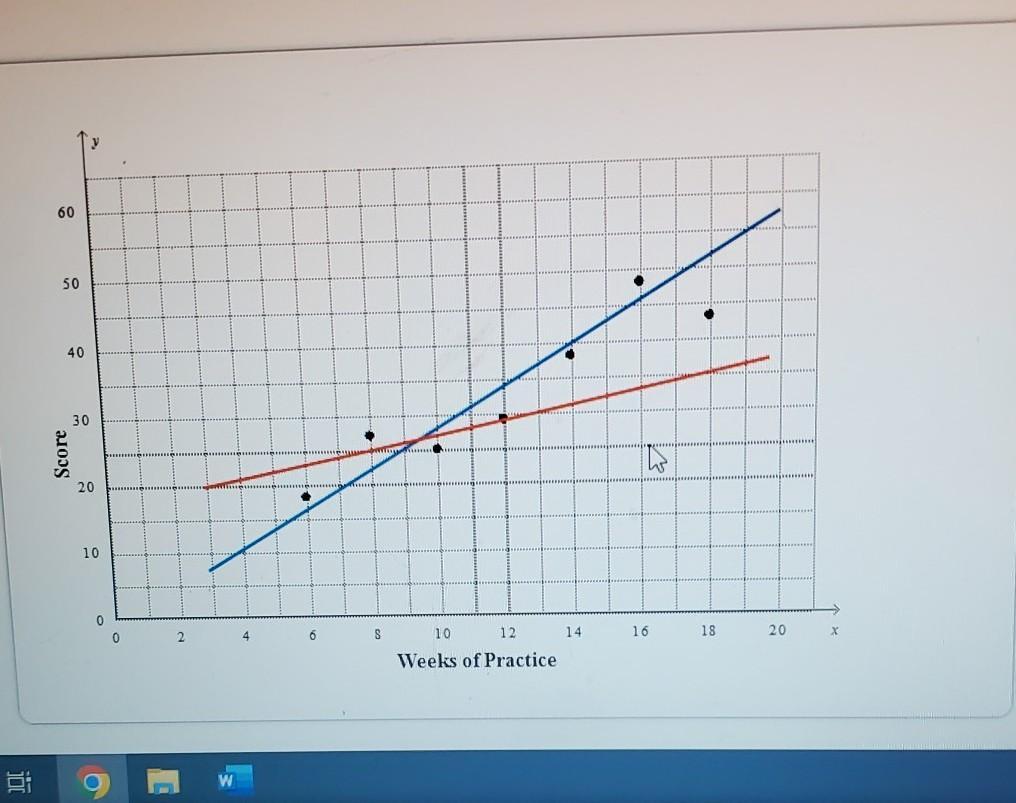
Answers
The line that models the data points better is Red, because it goes through one of the points.
What is data in math?Data is information that has been organized and processed in a meaningful way. It is the raw material of digital systems and the foundation of all computer-based operations. It can be stored, retrieved, and manipulated in a variety of ways, and it is used to generate insights, drive decisions, and build solutions. Data can come from a variety of sources, including manual entry, sensors, databases, and the internet.
This is a better model than Blue, because the data points are not all close to the line, and having the line go through one of the points ensures that the line is better representing the points. Additionally, having three points above the line and three points below the line helps to make the line a better model of the data points, as it is more evenly distributed.
To know more about data click-
https://brainly.com/question/14592520
#SPJ1
Alice is inventorying two different warehouses. In the first warehouse, she determines that there are 4.6X10 to the third power of boxes. In the second warehouse, she determines that there are 5X10 to the fourth power of boxes. What is the combined number of boxes in both warehouses?
PLEASE HELP!!!!
Answers
Answer:4.6 × 30= 138
5 × 40= 200
Step-by-step explanation:
Let f(x) = (x − 3)−² Find all values of c in (1, 4) such that f(4) − f(1) = f '(c)(4 − 1).
(Enter your answers as a comma-separated list. If an answer does not exist, enter DNE.)
c = ___.
Answers
The equation f(4) - f(1) = f'(c)(4 - 1), where f(x) = (x - 3)^(-2), asks for values of c in (1, 4) that satisfy the equation. By calculating f(4) and f(1), we find they are both equal to 1. The derivative of f(x) is -2(x - 3)^(-3). Substituting these values, we get 3/4 = f'(c)(3). However, since f'(x) is negative in the interval (1, 4) and the left side is positive, there is no value of c in that interval that satisfies the equation (DNE).
To find the values of c in the interval (1, 4) such that f(4) - f(1) = f'(c)(4 - 1), where f(x) = (x - 3)^(-2), we need to apply the Mean Value Theorem for derivatives.
Let's start by calculating f(4) and f(1):
f(4) = (4 - 3)^(-2) = 1
f(1) = (1 - 3)^(-2) = 1/4
Now, let's calculate the derivative of f(x):
f'(x) = d/dx[(x - 3)^(-2)]
= -2(x - 3)^(-3)
Next, we substitute these values into the equation f(4) - f(1) = f'(c)(4 - 1):
1 - 1/4 = f'(c)(3)
We simplify the equation:
3/4 = f'(c)(3)
To solve for c, we need to find the value of c in the interval (1, 4) that satisfies this equation. Notice that f'(x) = -2(x - 3)^(-3) is negative for all x in the interval (1, 4). Since the left side of the equation is positive (3/4 > 0), there is no value of c in the interval (1, 4) that satisfies the equation. Therefore, the answer is DNE (does not exist).
To know more about the Mean Value Theorem, refer here:
https://brainly.com/question/30403137#
#SPJ11