The sum of three consecutive odd integers is 459. What are the integers? (show your work please)
Answers
Answer:
151+153+155
Step-by-step explanation:
First you divide 459/3. That equals 153. Now you need 3 integers that add to 459. The first integer is 153 and now you subtract and add equal parts from it to get your other two. You subtract 153 by two and get 151. Then you add 153 by 2 and get 155.
Related Questions
John and his family are moving to a new house. He must pack items from his room into rectangular prism boxes that have a volume of 3r+ 9x + 6 ft. He knows the height of the box is 3 feet. In terms of x, what are the other dimensions of the box?
Answers

A restaurant charges a $100 setup fee, plus $15 per guest, to host a private party.
The table below shows the cost of hosting a private party for a certain number of
guests.

Answers
Answer: 775
Step-by-step explanation: $15 for each guest (so you need to multiply 15 by 45) then add the $100 setup fee!
5. Elsa spent half of her allowance going to a movie. But
hen she walked the dog to earn another $8. What is her
veekly allowance if she ended with $14?
Answers
What are the coordinates of point B on AC such that the ratio of AB to AC is 5:6
Answers
Coordinates of point B are (5x₂+6x₁)/11 and (5y₂+6y₁)/11
What is the section formula in coordinate geometry?
When the line segment is divided internally in the ratio m:n, we use this formula. That is when point C lies somewhere between points A and B. p= (mx₂+nx₁)/(m+n) & q= (my₂+ny₁)/(m+n)
Given here, point B on AC such that the ratio of AB to AC is 5:6
Let the point B(p,q) internally divide the line joining points A(x₁, y₁) and C(x₂, y₂) in the ratio m : n , then,
p= (mx₂+nx₁)/(m+n)
q= (my₂+ny₁)/(m+n)
Here. m=5 and n=6
p=(5x₂+6x₁)/11 , q=(5y₂+6y₁)/11
Hence, the Coordinates of point B are (5x₂+6x₁)/11 and (5y₂+6y₁)/11
I hope this helps <3
Please check your answer cause this is my last question

Answers
The interest rate would be 13%.
What is the simple interest?
Simple Interest (S.I.) is the method of calculating the interest amount for a particular principal amount of money at some rate of interest. For example, when a person takes a loan of Rs. 5000, at a rate of 10 p.a. for two years, the person's interest for two years will be S.I. on the borrowed money.
To find the interest rate, we can use the formula for simple interest:
I = Prt
where I is the amount of interest earned, P is the principal (the initial amount of money deposited), r is the interest rate, and t is the time in years.
In this case, we know that I = $3,900, P = $10,000, and t = 3 years. We can use this information to solve for r:
I = Prt
$3,900 = $10,000r3
r = $3,900/($10,000*3)
r = 0.13 or 13%
Hence, the interest rate is 13%.
To learn more about the simple interest, visit:
https://brainly.com/question/20690803
#SPJ1
(17\%) Problem 1: An amusement park ride rotates around a fixed axis such that the angular position of a point on the ride follows the equation: θ(t)=a+ bt^2 −ct 63 where a=0.3rad,b=0.65rad/s ^2 and c=0.035rad/s ^3 . Randomized Variables a=0.3radb=0.65rad/s ^2 c=0.035rad/s ^3
a 20\% Part (a) Determine an equation for the angular speed of the ride as a function of time, 0(t). Write your answer using the symbols a,b, and c. instead of their numerical values. a 20% Part (b) Besides at t=0, at what time t, is the ride stopped? Give your answer in seconds. a 20% Part (c) What is the magnitude of the angular displacement of the ride in radians between times t=0 and t=t,? A 20% Part (d) Determine an equation for the angular acceleration of the ride as a function of time, a(t). Write your answer using the symbols a, b, and c, instead of their numerical values. D A 20% Part (e) What is the angular acceleration in rad/s^2 when the ride is at rest at t=tl?
Answers
The angular acceleration at rest is a(t = 0.054s) = 2b = 1.3 rad/s².
a) The angular speed (ω) of the ride is the first derivative of θ(t) with respect to time (t).Therefore, ω(t)= dθ/dt = 2bt-c...where a=0.3rad, b=0.65rad/s^2, and c=0.035rad/s^3.
b) The ride is stopped when the angular speed is zero.
Therefore,0 = 2bt - c...where b = 0.65rad/s^2, and c=0.035rad/s^3Solving for t gives:
t = c/2b = 0.054s
Therefore, the ride is stopped at t=0.054s.
c) The angular displacement of the ride between times t=0 and t=t is given by the definite integral of θ(t) from 0 to t.
∆θ = θ(t) - θ(0)
= (a + bt² - ct) - a
= bt² - ct.
where a=0.3rad, b=0.65rad/s^2, c=0.035rad/s^3
Hence, ∆θ(t) = (0.65t² - 0.035t)t
= 0.65t³ - 0.035t²...
where t is the time in seconds.
This is the magnitude of the angular displacement of the ride in radians between times t=0 and t=t.
d) The angular acceleration (α) of the ride is the second derivative of θ(t) with respect to time (t).
α(t) = d²θ/dt²
= 2b...
where a=0.3rad, b=0.65rad/s^2, and c=0.035rad/s^3
Therefore, the equation for the angular acceleration of the ride as a function of time is a(t) = 2b = 1.3 rad/s².
e) When the ride is at rest (i.e., ω(t) = 0), then t = c/2b = 0.054s (as found in part b).
Thus, the angular acceleration at rest is a(t = 0.054s) = 2b = 1.3 rad/s².
Learn more about angular acceleration from the given link
https://brainly.com/question/13014974
#SPJ11
Someone help and plz make sure it’s right

Answers
Answer:
a=40° hope I helped:)....
In a group of 50 people , 20 are vegetarian. If two people are selected at random, what is the mean of the probability distribution for the selected people who are vegetarian
Answers
The group of 50 people is the sample size of the probability distribution
The mean of the probability distribution for the selected people who are vegetarian is 0.8
How to determine the mean of the probability distributionThe given parameters are:
Sample Size, n = 50
Selected people, x = 20
Start by calculating the proportion (p)
\(p = \frac xn\)
So, we have:
\(p = \frac {20}{50}\)
\(p = 0.4\)
When 2 people are selected;
We have:
n = 2
So, the mean is:
\(\bar x = np\)
This gives
\(\bar x = 2 * 0.4\)
\(\bar x = 0.8\)
Hence, the mean of the probability distribution for the selected people who are vegetarian is 0.8
Read more about probability distribution at:
https://brainly.com/question/25638875
Find the most general antiderivative of f(u)=u2−6u4+9u. Note: Any arbitrary constants used must be an upper-case " C ". F(u)= Find the particular antiderivative that satisfies the following conditions: dxdy=6x−2+2x−1−7;y(1)=4 y=
Answers
The most general antiderivative of the function \( f(u) = u^2 - 6u^4 + 9u \) is \( F(u) = \frac{1}{3}u^3 - \frac{6}{5}u^5 + \frac{9}{2}u^2 + C \), where \( C \) represents an arbitrary constant. Thus, the particular antiderivative that satisfies the given conditions is \( -6x^{-1} + 2\ln|x| - 7x + 15 \).
To find the most general antiderivative of \( f(u) = u^2 - 6u^4 + 9u \), we can integrate each term separately. The antiderivative of \( u^2 \) is \( \frac{1}{3}u^3 \), the antiderivative of \( -6u^4 \) is \( -\frac{6}{5}u^5 \), and the antiderivative of \( 9u \) is \( \frac{9}{2}u^2 \). Adding these antiderivatives together with an arbitrary constant \( C \) gives us \( F(u) = \frac{1}{3}u^3 - \frac{6}{5}u^5 + \frac{9}{2}u^2 + C \).
To find the particular antiderivative that satisfies \( \frac{dy}{dx} = 6x^{-2} + 2x^{-1} - 7 \) and \( y(1) = 4 \), we integrate the given derivative function with respect to \( x \). The antiderivative of \( 6x^{-2} + 2x^{-1} - 7 \) is \( -6x^{-1} + 2\ln|x| - 7x + D \), where \( D \) is another arbitrary constant.
Then, applying the initial condition \( y(1) = 4 \) gives us \( -6(1)^{-1} + 2\ln|1| - 7(1) + D = 4 \). Simplifying this equation gives \( -6 + 2\ln(1) - 7 + D = 4 \), and solving for \( D \) gives \( D = 15 \). Thus, the particular antiderivative that satisfies the given conditions is \( -6x^{-1} + 2\ln|x| - 7x + 15 \).
Learn more about antiderivative here:
https://brainly.com/question/33243567
#SPJ11
A quilter created the following shape to use in a block for a new quilt. A six-sided figure with a large base of 10 and three-fifths inches. The side to the right of the base is 6 inches. The small side parallel to the base is 4 and one-fifth inches. There are two sides that form a point at a right angle. The smaller is 4 inches, and the larger is 5 inches. What is the area of the shape for the quilt block? seventy-three and three fifths in2 forty-one and four fifths in2 eighty-three and three fifths in2 one hundred forty-seven and one fifth in2

Answers
Answer:
(a) seventy-three and three fifths square inches
Step-by-step explanation:
You want to know the area of the quilt block shape shown.
Composite shapeThe shape can be considered to be composed of a rectangle 10.6 inches long, together with a right triangle with side lengths 4 and 5 inches.
AreaThe relevant area formulas are ...
triangle: A = 1/2bh
rectangle: A = bh
ApplicationThe area of the triangle is ...
A = 1/2(5 in)(4 in) = 10 in²
The area of the rectangle is ...
A = (10.6 in)(6 in) = 63.6 in²
The total area is ...
10 in² +63.6 in² = 73.6 in²
The area of the shape is 73 3/5 square inches.
<95141404393>
Find the area of the parallelogram with adjacent sides u=(5,4,0⟩ and v=(0,4,1).
Answers
The area of the parallelogram with adjacent sides u=(5,4,0⟩ and v=(0,4,1) is 21 square units. The area can be calculated with the cross-product of the two sides.
The area of a parallelogram is equal to the magnitude of the cross-product of its adjacent sides. It represents the amount of space enclosed within the parallelogram's boundaries.
The area of a parallelogram with adjacent sides can be calculated using the cross-product of the two sides. In this case, the adjacent sides are u=(5,4,0⟩ and v=(0,4,1).
First, we find the cross-product of u and v:
u x v = (41 - 04, 00 - 15, 54 - 40) = (4, -5, 20)
The magnitude of the cross-product gives us the area of the parallelogram:
|u x v| = √(\(4^2\) + \((-5)^2\) + \(20^2\)) = √(16 + 25 + 400) = √441 = 21
Therefore, the area of the parallelogram with adjacent sides u=(5,4,0⟩ and v=(0,4,1) is 21 square units.
Learn more about cross-product here:
https://brainly.com/question/29097076
#SPJ11
The function h is a quadratic function whose graph is a translation 7 units left and 9 units up of the parent function f(x) = x ^ 2 What is the equation of h in vertex form and in the form y = a * x ^ 2 + bx + c
Answers
Answer:D ( if you add +4 to the (x + 3)^2)
Step-by-step explanation:
Parent function is f(x) = x^2
A translation 3 units left gives y = )x + 3)^2
- and 4 up gives y = (x + 3)^2 + 4 - vertex form.
Standard form :
y = x^2 + 6x + 9 + 4
= x^2 + 6x + 13.
The equation is of the form h= x² + 14x +58.
What is function?An expression, rule, or law that defines a relationship between one variable (the independent variable) and another variable (the dependent variable).
Given:
f(x) = x²
As, graph is a translation 7 units left
f(x) = (x +7)²
and, 9 units up of the parent function
h= f(x) = (x +7)² + 9
So, equation of the form y = ax² + bx + c
h= x² + 14x +58
Learn more about function here:
https://brainly.com/question/12431044
#SPJ2
A bond with face value $1,000 has a current yield of 7.0% and a coupon rate of 9.0%.
Answers
The bond's coupon payment is $90 and the current market price is approximately $1,285.71.
To determine the current yield and coupon payment for a bond, to understand the definitions of these terms:
Current Yield: The current yield of a bond is calculated by dividing the annual coupon payment by the bond's current market price and expressing it as a percentage.
Coupon Rate: The coupon rate of a bond is the annual interest rate specified by the bond when it was issued. It represents the percentage of the bond's face value that will be paid as a coupon payment each year.
Given that the bond has a face value of $1,000, a current yield of 7.0%, and a coupon rate of 9.0%, we can calculate the coupon payment and the current market price of the bond.
Coupon Payment: The coupon payment is calculated by multiplying the face value of the bond by the coupon rate. In this case:
Coupon Payment = $1,000 ×9.0% = $90
Current Market Price: To find the current market price of the bond, we can use the formula for current yield and rearrange it as follows:
Current Yield = (Coupon Payment / Current Market Price) × 100
7.0% = ($90 / Current Market Price) × 100
Dividing both sides by 100 and rearranging the equation:
Current Market Price = $90 / (7.0% / 100)
Current Market Price = $90 / 0.07
Current Market Price ≈ $1,285.71
To know more about price here
https://brainly.com/question/33097741
#SPJ4
Pleaaas help meeeee pleasssss

Answers
Answer:
For the first row, it's 6, 12, 18, 24, 30
Second row: 4, 8, 12, 16, 20
Step-by-step explanation:
You're just counting by multiples of 6 for the first row and 4 for the second row. Denominator means the number underneath the fraction line
What is the area of the rectangle below? 8 17 O A. 68 sq. units O B. 25 sq. units O C. 136 sq. units O D. 50 sq. units

Answers
Answer:
136 sq units
Step-by-step explanation:
area = length * width
a = 17 * 8
a = 136 sq units
The area of the rectangle is given by the equation A = 136 units²
What is the Area of a Rectangle?The area of the rectangle is given by the product of the length of the rectangle and the width of the rectangle
Area of Rectangle = Length x Width
Given data ,
Let the area of the rectangle be represented as A
Let the length of the rectangle be L
Now , the value of L = 17 units
Let the width of the rectangle be W
Now , the value of W = 8 units
And , Area of Rectangle = Length x Width
On simplifying , we get
Area of rectangle A = 8 x 17
Area of rectangle A = 136 units²
Therefore , the value of A is 136 units²
Hence , the area of rectangle is 136 units²
To learn more about area of rectangle click :
https://brainly.com/question/15225905
#SPJ7
If you can’t see the picture good ask me to send another one
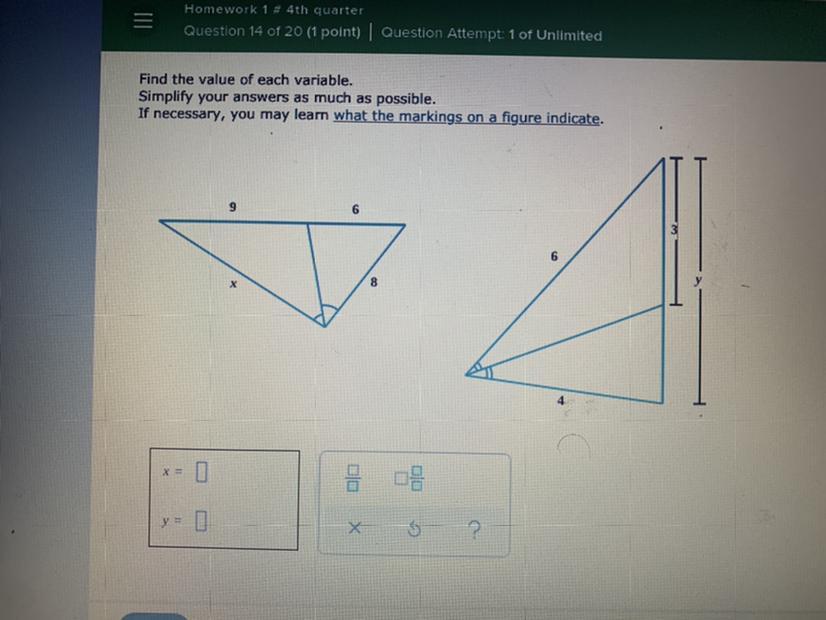
Answers
Here, we have two pairs of similar triangles.
Let's find the values of x and y.
• Sol,vin,g for x:
Given:
Length of longer base = 9
Length of shorter base = 5
Length of smaller leg = 8
Let's solve for x.
Since the triangles are similar, the corresponding sides will be in proportion.
To solve for x, apply the proportionality equation:
\(\frac{9}{x}=\frac{6}{8}\)Cross multiply and solve for x:
\(\begin{gathered} 6x=9*8 \\ \\ 6x=72 \\ \\ \text{ Divide both sides by 6:} \\ \frac{6x}{6}=\frac{72}{6} \\ \\ x=12 \end{gathered}\)• Solving for y:
Given:
Length of longer base = 3
Length of longer leg = 6
Length of smaller leg = 4
Length of total base = y
To solve for y, we have the equation:
\(\frac{6}{3}=\frac{4}{y-3}\)Cross multiply and solve for y:
\(\begin{gathered} 6(y-3)=4*3 \\ \\ 6y-6(3)=12 \\ \\ 6y-18=12 \\ \\ \text{ Add 18 to both sides:} \\ 6y-18+18=12+18 \\ \\ 6y=30 \\ \\ \text{ Divide both sides by 6:} \\ \frac{6y}{6}=\frac{30}{6} \\ \\ y=5 \end{gathered}\)ANSWER:
• x = 12
• y = 5
Hansen played an arcade game that cost 25 tokens PER GAME. In six games, Hansen won 0 tokens, 10 tokens, 50 tokens, 0 tokens, 5 tokens, and 10 tokens. What is the change in the number of tokens Hansen has?
Answers
Answer:
150-75=75, so a change of -75
Step-by-step explanation:
He spent 150 tokens and only got 75 tokens back
Which of the following have both 2 and -5 as solutions.a. x2 + 3× - 10 = 0b. x2- 3x -10=0c. x2 + 7× +10=0d. x2 -7x +10=0
Answers
the equation (\(x^2 + 3x - 10 = 0\)) has both 2 and -5 as solutions. Therefore the correct option is a.
To determine which equation(s) have both 2 and -5 as solutions, substitute these values into each equation and see if they satisfy the equation. Let's check each option:
a. \(x^2 + 3x - 10 = 0\)
Substituting x = 2:
\((2)^2 + 3(2) - 10 = 4 + 6 - 10 = 0\)
Substituting x = -5:
\((-5)^2 + 3(-5) - 10 = 25 - 15 - 10 = 0\)
Both 2 and -5 satisfy the equation, so option a has both 2 and -5 as solutions.
b. \(x^2 - 3x - 10 = 0\)
Substituting x = 2:
\((2)^2 - 3(2) - 10 = 4 - 6 - 10 = -12\)
Substituting x = -5:
\((-5)^2 - 3(-5) - 10 = 25 + 15 - 10 = 30\)
Neither 2 nor -5 satisfy the equation, so option b does not have both 2 and -5 as solutions.
c. \(x^2 + 7x + 10 = 0\)
Substituting x = 2:
\((2)^2 + 7(2) + 10 = 4 + 14 + 10 = 28\)
Substituting x = -5:
\((-5)^2 + 7(-5) + 10 = 25 - 35 + 10 = 0\)
Only -5 satisfies the equation, so option c does not have both 2 and -5 as solutions.
d. \(x^2 - 7x + 10 = 0\)
Substituting x = 2:
\((2)^2 - 7(2) + 10 = 4 - 14 + 10 = 0\)
Substituting x = -5:
\((-5)^2 - 7(-5) + 10 = 25 + 35 + 10 = 70\)
Only 2 satisfies the equation, so option d does not have both 2 and -5 as solutions.
In conclusion, the equation in option a (\(x^2 + 3x - 10 = 0\)) has both 2 and -5 as solutions.
To learn more about equation
https://brainly.com/question/17482667
#SPJ11
which fraction is NOT equivalent to 8/12
Answers
Answer:
32/60 is not a equivalent fraction of 8/12
I hope this helps you.
The area of the top side of a piece of sheet metal is given below. The sheet metal is submerged horizontally in 7 feet of water. Find the fluid force on the top side. (The weight-density of water is 62.4 pounds per cubic foot.) 4 square feet lb
Answers
The fluid force on the sheet metal's top side when submerged horizontally in 7 feet of water is 12441.6 lb.
Given,
The area of the top side of a piece of sheet metal = 4 square feet
The sheet metal is submerged horizontally in 7 feet of water.
Fluid Force on the top side can be found as follows,
Formula used:
Fluid Force = weight-density × volume × depth of fluid
Fluid Force = 62.4 × volume × 7
As the sheet metal is completely submerged, the volume is equal to the area of the sheet metal.
Volume = Area × Depth
= 4 × 7
= 28
Fluid Force = 62.4 × 28 × 7
= 12441.6 lb
Thus, the fluid force on the sheet metal's top side when submerged horizontally in 7 feet of water is 12441.6 lb.
To know more about the fluid force, visit:
brainly.com/question/13165826
#SPJ11
Therefore, the fluid force on the top side is 55838.08 lb.
Given, the area of the top side of a piece of sheet metal is 4 square feet and it is submerged horizontally in 7 feet of water.
The weight-density of water is 62.4 pounds per cubic foot.To find: the fluid force on the top side.Solution:Fluid force formula is given by,
F = ρ * g * V
Where, ρ is the density of the fluidg is the acceleration due to gravityV is the volume of the fluid displaced.Furthermore, the volume of fluid displaced is equal to the volume of the metal sheet submerged in the water.
Therefore,Volume of fluid displaced = Volume of metal sheet submerged in the water = area of metal sheet * depth submerged
Volume of metal sheet submerged in the water = 4 square feet * 7 feet
= 28 cubic feet
Now, calculate the fluid force on the top side of the metal sheet by using the fluid force formula.
F = ρ * g * V
Here, the density of water,
ρ = 62.4 pounds per cubic foot
g = 32.2 ft/s² (the acceleration due to gravity)
V = 28 cubic feet∴
F = 62.4 * 32.2 * 28 lb
= 55838.08 lb
Therefore, the fluid force on the top side is 55838.08 lb.
To know more about area visit;
brainly.com/question/30307509
#SPJ11
What is the value of g^-1(1)

Answers
According to the graph, g (-4) = 1, so g ⁻¹(1) = -4.
Step-by-step explanation:
According to the graph, g (-4) = 1, so g ⁻¹(1) = -4.
Hope this helps!
7)
Ella started exercising. Which division expression means she lost 5 pounds every 2 weeks?
5
A)
B)
0
D)
JU
Answers
Answer:
-5/2
Step-by-step explanation:
Comment factoriser (x-4)^{2}-36
Answers
Answer:
Step-by-step explanation:
to factorize \((x-4)^{2} -36\)
(x-4-6) * (x - 4 / 6)
(x-10) * (x+2)
does anybody knows this if u do please tell me the 3 facts this is due tomorrow!!:[

Answers
In a parallelogram, the sum of the measures of the angles is ______?
Answers
Answer: 360
Step-by-step explanation:
Answer is 360 degrees
a parallelogram can be divided into two triangles
The Sum of the angles of each triangle is 180°
2 x 180 =360
Answer:
360
Step-by-step explanation:
Formula to find the sum of angles of any shape
(n-2)x180
(4-2)x180
2x180=360
Hence the sum of angles of a parallelogram is 360
Someone help please.

Answers
Answer:
Translation (the +5)
Dilation (the x 4)
Compression (the 3 to 1/3, and the x to 2-x)
Step-by-step explanation:
Brainliest, please!
HOW MANY ZEROS WILL BE IN THE PRODUCT OF 5 TIMES 10EXPONT OF 5 EXPLAIN HOW YOU KNOW
Answers
Answer:
50 Zeros
Step-by-step explanation:
Since 10 is the exponent number and 5 is the base, then 5 would be written out 10 times but since you multiply that by 5, it's 50 zeros in total
Answer:
5 zeros because 5 × 10 is 50 if you multiply 5 by 10 5 times then there are 5 zeros.
Step-by-step explanation:
Consider f = x41 + x42, with x1 and x2 real. To minimize f, I set ∇f = 0 which yields x∗ = (0, 0)T . I claim that this is the global minimum. Explain my reasoning.
Answers
The function f is non-negative for all values of x1 and x2, and the critical point x* = (0, 0)T is the only possible point where f equals zero, we can conclude that x* = (0, 0)T is the global minimum of the function f.
To explain why the point x* = (0, 0)T is the global minimum of the function f = x1^2 + x2^2, we can analyze the properties of the function and its critical point.
First, let's consider the function \(f = x1^2 + x2^2\). This function represents the sum of the squares of two variables x1 and x2.
Since the squares of real numbers are always non-negative, the function f is non-negative for any values of x1 and x2. It means that f(x1, x2) ≥ 0 for all real values of x1 and x2.
Now, let's analyze the critical point x* = (0, 0)T, which we found by setting the gradient of f equal to zero (∇f = 0).
∇f = (2x1, 2x2)
Setting ∇f = 0, we have:
2x1 = 0
2x2 = 0
From these equations, we can see that x1 = x2 = 0 satisfies the conditions. Therefore, (0, 0)T is a critical point of the function.
To determine if x* = (0, 0)T is the global minimum, we need to check the behavior of f around x*.
If we consider any other point (x1, x2) ≠ (0, 0), the value of f will be greater than zero, as f(x1, x2) ≥ 0 for all (x1, x2).
Therefore, since the function f is non-negative for all values of x1 and x2, and the critical point x* = (0, 0)T is the only possible point where f equals zero, we can conclude that x* = (0, 0)T is the global minimum of the function f.
In other words, no other point (x1, x2) can produce a smaller value for f than (0, 0)T, making it the global minimum.
To know more about global minimum refer here:
https://brainly.com/question/31403072
#SPJ11
At a certain location a river is 12 meters wide. At this location the depth of the river in meters has been measured at 3 meter intervals.The cross-section is shown below. 3 3 3 3 0.5 2.3 12.9 2.1 13.8 (a) Use Simpson's rule with the five depth measurements to calculate the approximate area of the cross-section. 11 marks) (b) The river flows at 0.4 meters per second Compute the approximate volume of water flowing through the cross-section in 10 seconds
Answers
According to the information we can infer that the approximate area of the cross-section is 35.5 square meters. Additionally, the approximate volume of water flowing through the cross-section in 10 seconds is 142 cubic meters.
How to calculate the approximate area of the cross-section using Simpson's rule?To calculate the approximate area of the cross-section using Simpson's rule, we divide the width of the river (12 meters) into intervals and consider the depth measurements at each interval. Given the depth measurements:
3, 3, 3, 3, 0.5, 2.3, 12.9, 2.1, 13.8We use Simpson's rule to estimate the area by applying the formula:
Area ≈ (Width/3) * [f(x₀) + 4f(x₁) + 2f(x₂) + 4f(x₃) + ... + 2f(xₙ₋₂) + 4f(xₙ₋₁) + f(xₙ)]Using the given depth measurements, we substitute them into the formula and calculate:
Area ≈ (12/3) * [3 + 4(3) + 2(0.5) + 4(2.3) + 2(12.9) + 4(2.1) + 13.8]Area ≈ 35.5 square metersAccording to the information, the approximate area of the cross-section is 35.5 square meters.
How to calculate the approximante volume of water flowing through the cross-section?To calculate the approximate volume of water flowing through the cross-section in 10 seconds, we multiply the area of the cross-section by the velocity of the river.
Given the velocity of the river is 0.4 meters per second, and the time is 10 seconds:
Volume ≈ Area * Velocity * TimeVolume ≈ 35.5 * 0.4 * 10Volume ≈ 142 cubic metersAccording to the information, the approximate volume of water flowing through the cross-section in 10 seconds is 142 cubic meters.
Learn more about Simpson's rule in: https://brainly.com/question/32151972
#SPJ1
distributive property of 3(2x + 7)
Answers
Answer:
6x+21
Step-by-step explanation:
Answer:
36
Step-by-step explanation: