The rate of change of the gender ratio for the United States during the twentieth century can be modeled as g(t) = (1. 68 · 10^−4)t^2 − 0. 02t − 0. 10
where output is measured in males/100 females per year and t is the number of years since 1900. In 1970, the gender ratio was 94. 8 males per 100 females.
(a) Write a specific antiderivative giving the gender ratio.
G(t) = _______________ males/100 females
(b) How is this specific antiderivative related to an accumulation function of g?
The specific antiderivative in part (a) is the formula for the accumulation function of g passing through (t, g) =
Answers
Answer:
(a) G(t) = (1.68 × 10^-4) × (1/3) t^3 - (0.02/2) t^2 - 0.10t - 2445.84
(b) A(t) = G(t) - G(1900) = (1.68 × 10^-4) × (1/3) (t^3 - 1900^3) - (0.02/2) (t^2 - 1900^2) - 0.10(t - 1900)
Step-by-step explanation:
(a) The antiderivative of g(t) can be found by integrating each term of the function with respect to t:
∫g(t) dt = ∫(1.68 × 10^-4)t^2 dt - ∫0.02t dt - ∫0.10 dt
= (1.68 × 10^-4) × (1/3) t^3 - (0.02/2) t^2 - 0.10t + C
where C is the constant of integration.
To find the specific antiderivative G(t) that passes through the point (1970, 94.8), we can use this point to solve for C:
94.8 = (1.68 × 10^-4) × (1/3) (1970)^3 - (0.02/2) (1970)^2 - 0.10(1970) + C
C = 94.8 + (1.68 × 10^-4) × (1/3) (1970)^3 - (0.02/2) (1970)^2 - 0.10(1970)
C ≈ -2445.84
Therefore, the specific antiderivative that gives the gender ratio is:
G(t) = (1.68 × 10^-4) × (1/3) t^3 - (0.02/2) t^2 - 0.10t - 2445.84
(b) The accumulation function of g is the integral of g with respect to t, or:
A(t) = ∫g(t) dt = G(t) + C
where C is the constant of integration. We can find the value of C using the initial condition given in the problem:
A(1900) = ∫g(t) dt ∣t=1900 = G(1900) + C = 0
Therefore, C = -G(1900), and the accumulation function of g is:
A(t) = G(t) - G(1900) = (1.68 × 10^-4) × (1/3) (t^3 - 1900^3) - (0.02/2) (t^2 - 1900^2) - 0.10(t - 1900)
To know more about antiderivative refer here
https://brainly.com/question/31385327#
#SPJ11
Related Questions
compute the number of ways you can select 3 elements from 7 elements.
a. 343
b. 10
c. 21
d. 35
Answers
The number of possible ways in which we can select 3 elements from 7 elements are given in option d. 35.
There are a total of 7 elements and we can to select 3 elements out of them.
We have to apply the permutation and combination here in order to find the answer,
The formula is ⁿCₐ
Where, C represents combination,
n is the total number of combination,
a is the number of selections that we have to do,
ⁿCₐ = n!/(n-a)!a!
Now, putting n = 7 and a = 3,
ⁿCₐ = 7!/(4)!3!
ⁿCₐ = 35
So, the total number of ways possible are 35.
To know more about combination, visit,
https://brainly.com/question/11732255
#SPJ4
Let U = {a, b, c, d, e}.
Let A = {a, b, c}, B = {b, c, d, e} and C = {a, b, e}.
Which one of the following relations is not a function from B to U?
Select one:
a.
{(b, b), (e, c), (d, b), (c, a)}
b.
{(d, a), (c, e), (e, e), (c, a)}
c.
{(e, a), (b, a), (d, a), (c, b)}
d.
{(e, e), (b, c), (d, a), (c, b)}
Answers
The relation that is not a function from B to U is option b.
To determine which relation is not a function from B to U, we need to check if each element in B is associated with exactly one element in U. If there is any element in B that is associated with more than one element in U, then it is not a function.
Let's analyze each of the options:
a. {(b, b), (e, c), (d, b), (c, a)} This relation is a function because each element in B is associated with exactly one element in U.
b. {(d, a), (c, e), (e, e), (c, a)} This relation is not a function because the element 'c' in B is associated with both 'e' and 'a' in U. The element 'c' should be associated with exactly one element in U for it to be a function.
c. {(e, a), (b, a), (d, a), (c, b)} This relation is a function because each element in B is associated with exactly one element in U.
d. {(e, e), (b, c), (d, a), (c, b)} This relation is a function because each element in B is associated with exactly one element in U.
Among the given options, option b is the relation that is not a function from B to U.
To know more about relation , visit
brainly.com/question/6241820?
#SPJ11
determine whether the underlined number is a statistic or a parameter a sample of professors is selected and it is found that 40% own a television
Answers
The underlined number is a statistic.
Is the underlined number a sample statistic?In this scenario, the underlined number, 40%, represents the proportion of professors in a sample who own a television. A statistic is a numerical value that describes a characteristic of a sample. In contrast, a parameter is a numerical value that describes a characteristic of an entire population. Since the information provided is based on a sample of professors, the 40% is a statistic.
The distinction between statistics and parameters in statistical analysis. Statistics are used to make inferences about populations based on sample data. Parameters, on the other hand, provide information about the entire population. Understanding this distinction is crucial for accurate data interpretation and drawing meaningful conclusions.
Learn more about Statistic
brainly.com/question/32201536
#SPJ11
Where does the money come from that is used to pay taxes?
o Money to pay taxes comes from net income.
Money to pay taxes comes from sales tax.
Money to pay taxes comes from income earned.
Money to pay taxes comes from a budget.
Answers
Answer:
Your correct answer is going to be the third option
Step-by-step explanation:
Identify the type I error and the type II error that correspond to the given hypothesis.
The percentage of households with Internet access is greater than 60 %.
Answers
Answer: Type I error and Type II error are associated with hypothesis testing, where we test a hypothesis by collecting data and analyzing it.
For the given hypothesis, we can set up the null hypothesis as follows:
H0: The percentage of households with Internet access is less than or equal to 60%.
And the alternative hypothesis as:
Ha: The percentage of households with Internet access is greater than 60%.
Now, a Type I error occurs when we reject the null hypothesis (i.e., conclude that the percentage of households with Internet access is greater than 60%) when it is actually true. This means that we would be making a false claim that the percentage of households with Internet access is greater than 60%, when it is not.
On the other hand, a Type II error occurs when we fail to reject the null hypothesis (i.e., conclude that the percentage of households with Internet access is less than or equal to 60%) when it is actually false. This means that we would be missing the truth that the percentage of households with Internet access is greater than 60%.
So, in the context of the given hypothesis, a Type I error would be to conclude that the percentage of households with Internet access is greater than 60% when it is actually less than or equal to 60%, and a Type II error would be to fail to conclude that the percentage of households with Internet access is greater than 60% when it is actually greater than 60%.
Given: r = 3 + 6 sin(θ)
Part a: Graph the polar curve.
Part b: Give the formula involving one or more integrals for the area inside the inner loop for the polar curve. Do not evaluate the integral.
Part c: Give the formula for the length of the outer loop for the polar curve. Do not evaluate the integral.
Answers
(a) The polar curve is a cardioid. (b) The inner loop can be expressed as 1/2 times the integral of (r^2) dθ from θ = -π/6 to θ = π/6. (c) The formula for the length of the outer loop can be expressed as the integral of the square root of (r^2 + (dr/dθ)^2) dθ from θ = -π/3 to θ = π/3.
(a) The given polar equation r = 3 + 6sin(θ) represents a cardioid. A cardioid is a heart-shaped curve, and in this case, the center of the cardioid is at (3, 0).
(b) To find the formula for the area inside the inner loop, we can use the formula for the area bounded by a polar curve, which is 1/2 times the integral of (r^2) dθ over the desired interval. In this case, the interval is from θ = -π/6 to θ = π/6. Thus, the formula for the area inside the inner loop is 1/2 times the integral of (3 + 6sin(θ))^2 dθ from θ = -π/6 to θ = π/6.
(c) The length of the outer loop can be found using the arc length formula for polar curves. The formula is the integral of the square root of (r^2 + (dr/dθ)^2) dθ over the desired interval. In this case, the interval is from θ = -π/3 to θ = π/3. Therefore, the formula for the length of the outer loop is the integral of the square root of (3 + 6sin(θ))^2 + (6cos(θ))^2 dθ from θ = -π/3 to θ = π/3.
Learn more about polar curve here:
https://brainly.com/question/27548409
#SPJ11
a box has dimensions of 3.5 cm by 4.0 cm by 8.0 cm. the volume of the box in milliliters and liters is:
Answers
Step-by-step explanation:
3.5cm===> 35mm===> 3.5e–6 lit
4.0cm===> 40mm===> 4.0e–6 lit
8.0cm===> 80mm===> 8.0e–6 lit
V(mm)=35×40×80=112000mm³
V(lit)=(3.5×4.0×8.0)×e–6=112e–6lit³
What is the solution to the system of equations? -1/2x+1/2y=-1 x-y=2
Answers
y=14
have a good day
have a good dayyy
Express your answer in scientific notation\(0.00045 - 2.5 \times 10 {}^{ - 5} \)
Answers
The given expression is
\(0.00045-2.5\times10^{-5}\)First, we express the first number in scientific notation. We have to make sure that both scientific notations have the same exponent.
\(45\times10^{-5}-2.5\times10^{-5}\)Then, we subtract the coefficients.
\((45-2.5)\times10^{-5}=42.5\times10^{-5}=4.25\times10^{-4}\)Therefore, the answer is\(4.25\times10^{-4}\)write an equation for the line that is parellel to the given line and that passes through the given point?
y = 2x + 7; (3, 11)
a.y = 2x – 19
b.y=1/2x+5
c.y= -1/2x-5
d.y = 2x + 5
Answers
Answer:
y = 2x + 5 (answer d)
Step-by-step explanation:
Parallel lines have the same slope, and thus, if we're given y = 2x + 7, we know that the slope of the 'new' line is 2. This 'new line' passes through (3, 11). Begin with the point-slope formula y - k = m(x - h) and substitute 3 for h, 11 for k and 2 for m:
y - 11 = 2(x - 3)
Rewriting this in slope-intercept form, we get:
y = 2x - 6 + 11. or y = 2x + 5 (answer d)
Solve for x.
18
61x
Set up the proportion.
X
[?
X
6
=
X
Enter
Answers
The solution is \(X = 122.0\), and the proportion in the equation is, \(X / 6 = 61x / 18\).
What manner of equation would that be?The notion of an equation in algebra is a theoretical statement that demonstrates the equality of two formalisms. For instance, the expression 3x + 5 = 14 consists of the two solutions 3x + 5 and 14, that are separated by the 'equal' sign.
A ratio is it an expression?Every utterance can be composed of a numerical value, a constants, or a mixture of numerals, constants, or operation signs. Two expressions joined by an equation form an equation.
We can cross-multiply,
18 * X = 61x * 6
Simplifying the right-hand side,
\(18 * X = 366x\)
Dividing both sides by \(18x\),
\(X / 6 = 366x / 18x\)
Simplifying:
\(X / 6 = 61 / 3\)
\(X / 6 = 20.3333\)
Multiplying both sides by \(6\):
\(X = 122.0\)
Therefore, the solution is \(X = 122.0\), and the proportion is:
\(X / 6 = 61x / 18\)
To know more about equation visit:
https://brainly.com/question/10413253
#SPJ1
The solution is x = 3.5633 of 18 / x = 61x / 6.
What is fraction?
A fraction is a mathematical term that represents a part of a whole or a ratio between two quantities. It is a way of expressing a number as a quotient of two integers, where the top number is called the numerator, and the bottom number is called the denominator.
To set up the proportion, we need to equate the ratios of the corresponding terms in the two fractions, which gives:
18 / x = 61x / 6
Simplifying the right-hand side by dividing both the numerator and denominator by 6 gives:
18 / x = 61x / 6
18 / x = 10.1667x
Now we can cross-multiply to get:
18 * 10.1667x = x * 6
Simplifying and dividing both sides by 6:
(18 * 10.1667) * x = 6 * x
x = 3.5633
Therefore, the solution is x = 3.5633.
To learn more about fractions from the given link:
https://brainly.com/question/10354322
#SPJ1
Write the numbers from least to greatest: 3.1, 0, -3.9, -4.8, -4.08, 3.
Answers
Answer: -4.8, -4.08, -3.9, 0, 3, 3.1
Step-by-step explanation:
Think of these numbers on a number line. Starting at zero number to the right all positive numbers ex: 0,1,2,3,4
Then, starting at zero moving left number negative numbers ex: -4,-3,-2,-1,0
answer FAST please and i will give brainliest

Answers
This is simply a rearranged version of Pythagoras’ theorem
Salary Raise: Men According to the same survey quoted in Problem 13, of the men interviewed, 20% had asked for a raise and 59% of the men who had asked for a raise received the raise. If a man is selected at random from the survey population of men, find the following probabilities: P(man asked for a raise); P(man received raise, given he asked for one); P(man asked for raise and received raise).
Answers
The evaluated probabilities for the given question are 0.20 for the men who asked for promotion, 0.59 for the men who received the promotion when asked, and 0.118 for men who asked for promotion and received.under the condition that from the men interviewed 20% had asked for a promotion and 59% of the men who had asked for a promotion and received.
Then,
P(man asked for a promotion)
= 20/100
= 0.20
P(man received promotion, given he asked for one)
= 59/100
= 0.59
P(man asked for promotion and received )
= P(man asked for a promotion) x P(man received promotion, given he asked for one)
= 0.20 x 0.59
= 0.118
Probability is considered as the percentage of an event taking place in a specific time frame, in a given place. It is said to be a great aid in the horizons of science and mathematics.
To learn more about probability,
https://brainly.com/question/30390037
#SPJ4
Find ƒ(−8) if ƒ(x) = −9x – 12
Answers
A function in the mathematics from a set X to a set Y allocates exactly one element of Y to each element of X. The sets X and Y are collectively referred to as function's domain and codomain, respectively. Here f(x)= 60.
What is a function?A function in the mathematics from a set X to a set Y allocates exactly one element of Y to each element of X. The sets X and Y are collectively referred to as function's domain and codomain, respectively.
Al-Biruni and Sharaf al-Din al-Tusi, two Persian mathematicians, are responsible for the earliest documented treatment of the concept of function. Initially, the functions represented the idealized relationship between two changing quantities. A planet's position, for the instance, depends on time. In the past, idea was developed with the infinitesimal calculus at the end of the 17th century, and the functions that were taken into consideration until the 19th century were differentiable (that is, they had a high degree of regularity). The realms of application of the concept of a function were substantially expanded at the conclusion of the 19th century when it was defined in terms of set theory.
The most common letters used to represent functions are f, g, and h. A function's value at an element of its domain x is denoted by the symbol f(x), and the numerical value obtained by evaluating the function at a specific input value is denoted by replacing x with that value. For example, the value of f at x = 4 is denoted by the symbol f(x) (4). The value of the function at, say, x = 4 may be denoted by E|x=4 when the function has no name and is represented by the expression E.
if, f(x)= (-8),
f(-8)= (-9)*(-8)-12 = 60
To know more about domain visit: https://brainly.com/question/28135761
#SPJ9
Write 28/25 as a percentage
Answers
To write 28/25 as a percentage we need to multiply the fraction by 100 as follows:
\(\frac{28}{25}=\frac{28}{25}\cdot100=112\text{ \%}\)For a field trip 12 students rode in bicycles and the rest filled up 13 magic school buses. How many students were in each magic school bus if a total of 259 students went on the field trip?
Answers
Match the vocabulary with the appropriate definition
Origin
Quadrant 111
(-; +)
Quadrant IV
(5)
Quadrant
(+,-)
Y Axis
Left to right (horizontal)
Quadrant 11
Up and down (vertical)
X Axis
1
(0,0)

Answers

5xy-x2t+2xy+3x2t asap
Answers
Answer:
7xy + 2x²t
Explanation:
5xy - x²t + 2xy + 3x²t
= (5xy + 2xy) + (3x²t - x²t)
= 7xy + 2x²t
need help on this, i dont really get the options cus i thought it would be 42

Answers
What are the linear factors of the function f(x)=2x3−x2−13x−6? Select each correct answer.
(x+3)
(2x−1)
(x−2)
(x+2)
(2x+1)
(x−3)
Last 3 are right
Answers
Given:
The function is
\(f(x)=2x^3-x^2-13x-6\)
To find:
The linear factors of the given function.
Solution:
We have,
\(f(x)=2x^3-x^2-13x-6\)
Splitting the middle terms, it can be rewritten as
\(f(x)=2x^3-(6-5)x^2-(15-2)x-6\)
\(f(x)=2x^3-6x^2+5x^2-15x+2x-6\)
\(f(x)=2x^2(x-3)+5x(x-3)+2(x-3)\)
\(f(x)=(x-3)(2x^2+5x+2)\)
Now, Splitting the middle term, we get
\(f(x)=(x-3)(2x^2+4x+x+2)\)
\(f(x)=(x-3)(2x(x+2)+1(x+2))\)
\(f(x)=(x-3)(x+2)(2x+1)\)
Therefore, the three linear factors of given function are (x-3), (x+2) and (2x+1). Hence, option 4, 5 and 6 are correct.
The linear factors of the given function f(x) = 2x³ - x² - 13x - 6 are;
(x - 3), (x + 2) and (2x + 1)
We are given the function;
f(x) = 2x³ - x² - 13x - 6
Let us start by splitting the terms at the middle. Since last term is 6, we can write 1 before x² as (6 - 5)
Also, we can write 13 as (15 - 2). Thus;
f(x) = 2x³ - (6 - 5)x² - (15 - 2)x - 6
Expanding gives us;
f(x) = 2x³ - 6x² + 5x² - 15x + 2x - 6
Factorizing gives us;
f(x) = 2x²(x - 3) + 5x(x - 3) + 2(x - 3)
(x - 3) is common and so we factorize it out to get;
f(x) = (x - 3)(2x² + 5x + 2)
Let us split (2x² + 5x + 2); 5 can be expressed as 4 + 1.Thus;
f(x) = (x - 3)(2x² + (4 + 1)x + 2)
f(x) = (x - 3)(2x² + 4x + x + 2)
Factorizing again gives;
f(x) = (x - 3)(2x(x + 2) + 1(x +2))
f(x) = (x - 3)(x + 2)(2x + 1)
In conclusion, the linear factors of the given function f(x) = 2x³ - x² - 13x - 6 are; (x - 3), (x + 2) and (2x + 1)
Read more at; https://brainly.com/question/17950065
3) In recent years, a growing array of entertainment options competes for consumer time. By 2004 , cable television and radio surpassed broadcast television, recorded music, and the daily newspaper to become the two entertainment media with the greatest usage (The Wall Street Journal, January 26, 2004). Researchers used a sample of 10 individuals and collected data on the hours per week spent watching cable television and hours per week spent listening to the radio. Use a .05 level of significance and test for a difference between the population mean usage for cable television and radio.
Answers
A study conducted in 2004 examined the usage of cable television and radio among 10 individuals to determine if there was a significant difference in the average hours spent on each medium. Using a significance level of 0.05, statistical analysis was performed to test for a disparity between the population mean usage of cable television and radio.
The researchers collected data on the number of hours per week spent watching cable television and listening to the radio from a sample of 10 individuals. The objective was to determine if there was a significant difference in the average usage between cable television and radio, considering the increasing competition among various entertainment options.
To test for a difference between the population mean usage for cable television and radio, a statistical hypothesis test was conducted. The significance level (α) of 0.05 was chosen, which means that the results would be considered statistically significant if the probability of obtaining such extreme results by chance alone was less than 5%.
The test compared the means of the two samples, namely the average hours spent watching cable television and listening to the radio. By analyzing the data using appropriate statistical techniques, such as a two-sample t-test, the researchers determined whether the observed difference in means was statistically significant or could be attributed to random variation.
After conducting the hypothesis test, if the p-value associated with the test statistic was less than 0.05, it would indicate that there was a significant difference between the population mean usage of cable television and radio. Conversely, if the p-value was greater than 0.05, there would be insufficient evidence to conclude a significant disparity.
To learn more about statistical click here: brainly.com/question/31577270
#SPJ11
Q. 1 Similar triangles have corresponding angles that are congruent and
corresponding sides that are...
O A. Congruent
B. Similar
C. Equal
O D. Proportional

Answers
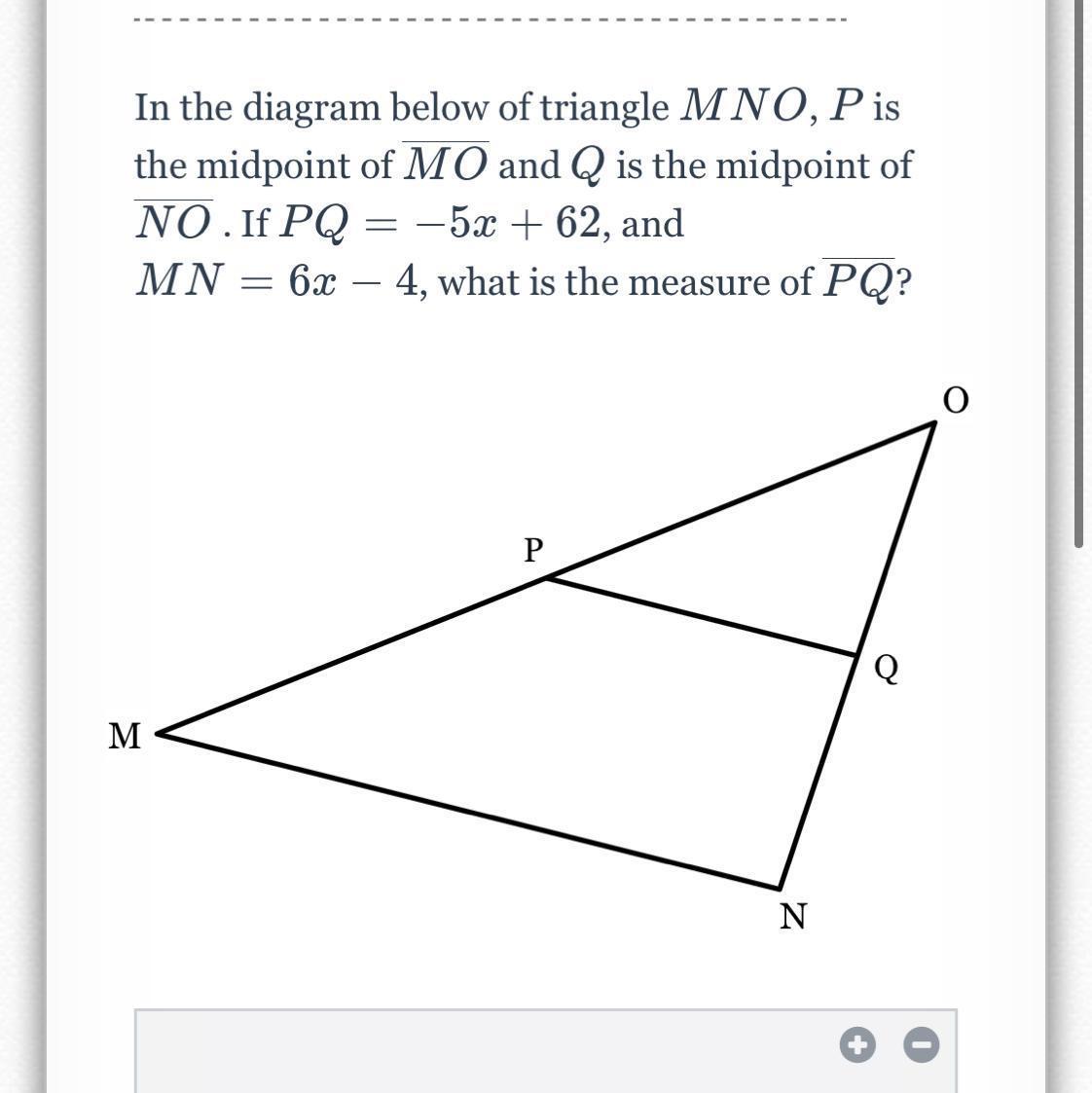
In the diagram below of triangle MNOP, P is the midpoint of MO and Q is the midpoint of NO. If PQ=5x+62 and MN=6x-4, what is the measure of PQ
Answers
The measure of length PQ will be 22 units.
What is the mid-point theorem?A triangle's third side is stated to be parallel to the line segment uniting its two midpoints, and it is also half as long as the third side.
Given:
PQ = 5x + 62, and MN = 6x-4
Now, using Mid- Point Theorem
PQ= 1/2 MN
-5x+ 62 = 1/2( 6x - 4)
-5x+ 62 = 3x - 2
-5x- 3x = -2 - 62
-8x = -64
x= 8
PQ= 5x+ 62 = -5(8) + 62 = -40 + 62 = 22
Hence, the measure of PQ is 22 units.
The missing image is attached below.
Learn more about the midpoint theorem here:
brainly.com/question/13677972
#SPJ1
Please help ill give whoever answers the best the brainliest answer :)

Answers
Answer:
3. Linear: f(x) = 1320(1.20)^2
Step-by-step explanation:
Exponential Growth Formula: f(x) = \(x_{0}\) × (1 + r)^x
f(x) is the value at time t.
x0 is the initial value at time t=0.
x0 = 1320
r = 20% = 0.2
Solve:
f(x) = \(x_{0}\) × (1 + r)^x
f(x) = 1320 × (1 + 0.2)^2
f(x) = 1320(1.2)^2
Answer: 3rd answer
Step-by-step explanation:
Because Purdue starts with 1320 employees, and then multiplies that by 1.2 each year. If x represents 3 years, Purdue has:
1320(1.2)^3
=1320(1.728)
=2280.96
que se descompone mas rápido, un caldo concentrado, como el pozole,o un diluido
Answers
el pozole se descompone porque tiene más azucares
Simplify (please show work if possible)

Answers
Answer: -6x^7
Step-by-step explanation:
2x^3 × (-3x^4)
=(2×-3) · (x^3 × x^4) ⇔ multiply the like terms
=-6 × [x^(3+4)] ⇔ the multiplication of exponents works as addition if same base
=-6x^7
Answer:
\(-6x^7\)
Step-by-step explanation:
So when doing this equation, you multiply the numbers, which is 2 × -3, and add the exponents, which is 3 + 4, so then you get the answer, and that is \(-6x^7\).
Please help me with this special right triangles/ trigonometry area

Answers
Answer: 1st 173 2nd 396
Step-by-step explanation: I hope this helps!
Please help me!! I need help

Answers
Answer:
c=l/--a^2+b^2=l/--45^2+20^2≈49.24429
Step-by-step explanation:
l/-- mean square root
^ means squared/ exponent
Answer:
Since they're asking you to find the missing sides "y" and "x" here's what you need to do....
Step-by-step explanation:
1) This is the 45-45-90 Triangle.
2) y = 20 becasue this is an isocelese triangle - meaning a triangle that has 2 sides of equal lengths!
3) in order to find x (which is the hyptoneus) you have to do
\(\sqrt{2}\) * leg (use on of the legs)
= \(20\sqrt{2}\)
also I think 45 degrees is there just to throw you off. And I'm pretty positive this is the correct answer, and i'm 100% sure that y = 20 is correct!
If Cos A = 9/41 and tan B = 28/45 angle A and B are in quadrant I find the value of Tan(A+B)
Answers
Explanation: i need points so 3/4572