The phenomenon that the sampling distribution of the sample mean can be approximated by a normal distribution as the sample size become large is called:______.
Answers
The phenomenon that the sampling distribution of the sample mean can be approximated by a normal distribution as the sample size become large is called: Central Limit Theorem.
What is Central Limit Theorem?The central limit theorem (CLT) of probability theory states that, under the assumption that all samples are of equal size and regardless of the population's actual distribution shape, the distribution of a sample variable approaches a normal distribution (i.e., a "bell curve") as the sample size increases.
Now,
As stated in the definition of the Central Limit Theorem, sampling distribution of the sample mean can be approximated by a normal distribution as the sample size become large with the help of the stated theorem.
To learn more about Central Limit Theorem, refer to the link:https://brainly.com/question/14806066
#SPJ4
Related Questions
Find the 72nd term of the arithmetic sequence -27, -11, 5, ...
Answers
Step-by-step explanation:
first identify the common difference
The first term which i will define by u⁰=-27
u¹=u⁰+(1)d where d is the common difference and u¹ is the second term
u¹=-27+d
-11=-27+d
d=27-11=16
The 72nd term would be u⁷¹ since we started from u⁰ as our first term:
Use the explicit relation given by:
u(n)=u⁰+(n)d
u(71)=-27+71(d)
u⁷¹=-27+71(16)
u⁷¹=-27+1136
u⁷¹=1109
Your goal is to design a new shape for a cereal container that will hold the same volume of cereal as a standard ceareal box and costs as little as possible to make. Assume that cardboard costs $0.05 per square inch. How cheaply can you package cereal?
These figures are available.
* triangular prism
* rectangular prism
* cube
* pyramid
* cone
* cylinder
* sphere
You need to keep the volume the same as the original, the surface area has to be less, and the price has to be the cheapest. The original volume was 192in^3. The surface area was 272in^2.
Answers
Answer:
$14.50
Step-by-step explanation:
To calculate the cost for manufacturing a standard cereal box, we must take in account its surface area. The volume will be used to estimate the amount of cereal, the box can contain. The box is a cuboid as standard cereal boxes are cuboid.
So, we will consider the surface area. Given are:
Length- 8 inches
Width- 3 inches
Height- 11 inches
We will find the surface area as : 2lw + 2wh +2lh
= (2x8x3) + (2x3x11) + (2x8x11)
= 48 + 66 + 176 = 290 square inches
Given is - the cost of manufacturing the box is $0.05 per square inch.
So, cost of manufacturing the box with 290 square inches area =
0.05 x 290 = $14.50
The answer is $14.50
The graph shows the relationship between the number
of cups of flour and the number of cups of sugar in
Angela's brownie recipe.
The table shows the same relationship for Jaleel's
brownie recipe.
Jaleel and Angela buy a 12-cup bag of sugar and divide
it evenly to make their recipes.
If they each use ALL of their sugar, how much FLOUR
do they each need?
Answers
Angela's use 6 cups of flour and Jaleel's use 19/3 cups of flour.
What is an expression?Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
Given that;
The graph shows the relationship between the number of cups of flour and the number of cups of sugar in Angela's brownie recipe.
And, The table shows the same relationship for Jaleel's brownie recipe.
Hence, The equation for Angela's brownie recipe is,
Two points on graph are (4, 2) and (2, 1)
⇒ y - 2 = (2 - 1)/ (4 - 2) (x - 4)
⇒ y - 2 = 1/2 (x - 4)
⇒ y - 2 = 1/2x - 2
⇒ y = 1/2x
And, The equation for Jaleel's brownie recipe is,
Two points on graph are (3/2, 1) and (3, 2)
⇒ y - 1 = (2 - 1)/ (3 - 3/2) (x - 4)
⇒ y - 1 = 2/3 (x - 4)
⇒ y - 1 = 2/3x - 8/3
⇒ y = 2/3x - 8/3 + 1
⇒ y = 2/3x - 5/3
So, For Jaleel and Angela buy a 12-cup bag of sugar.
The equation for Angela's brownie recipe is,
⇒ y = 1/2x
⇒ y = 1/2 × 12
⇒ y = 6
The equation for Jaleel's brownie recipe is,
⇒ y = 2/3x - 5/3
⇒ y = 2/3 × 12 - 5/3
⇒ y = 19/3
Thus, Angela's use 6 cups of flour and Jaleel's use 19/3 cups of flour.
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ1

(Factoring Algebraic Expressions MC) Factor −4x2 + 12x. 4x(−x + 3) −4x(x + 3) x(4x + 12) 4(−x2 + 12x)
Answers
The factorization of given polynomial is 4x(-x+3). Therefore, option A is the correct answer.
The given algebraic expression is -4x²+12x.
What are factors of polynomial?The factors are the polynomials which are multiplied to produce the original polynomial.
The factorization of the given polynomial is
-4x²+12x
= 4x(-x+3)
The factorization of given polynomial is 4x(-x+3). Therefore, option A is the correct answer.
To learn more about the factorization of polynomial visit:
https://brainly.com/question/16789195.
#SPJ1
Calculate the slope from the following two coordinates:
(-4,-5) and (-3,-2)
Answers
Well, find the change in y over change in x. You get three.over one. So your slope Is positive 3.
A jazz band wants to sell $2,800 worth of tickets. If each ticket costs $70, how many tickets will the band have to sell to meet its goal?
Answers
Answer:
40 tickets
Step-by-step explanation:
2800 = 70x
x is the number of tickets. You have to solve for x
Divide each side by 70
2800/70 = 70x/70
40 = x
100 points please help

Answers
Answer:
it is a
Step-by-step explanation:
Answer: it’s A because Richards Park charges an admission fee of $10 plus hourly which is the unit rate which stays at a constant price C=h the hours ($10+$5) is the correct answer. Hope this helps!
Step-by-step explanation:
Peter weighs is 105 kg. His wants to lose 500 g per week. How many weeks will it take for him to have a mass of 90 kg
Answers
Answer:
30
Step-by-step explanation:
500 g = 1/2 kg => 2 weeks he loses 1 kg
105 - 90 = 15 kg
So he needs to take 30 weeks in total. ( 15 * 2)
Let weeks be x
So
105-0.5x=900.5x=105-900.5x=15x=15/0.5x=30weeksA certain hallway in a crowded nightclub has a unique sound property. Every 2 feet closer to the stage you walk, the sound intensity (dB) doubles. If the threshold for pain is 127 dB, and the starting sound level is 2 dB, about how many feet down the hallway can you go until you start to feel pain
Answers
The number of feet down the hallway where you go until you start to feel pain is 14 feet.
What is geometric progression GP?A sort of sequence known as geometric progression (GP) is one in which each following phrase is created by multiplying every preceding term by such a fixed number, or "common ratio."
The general form of GP is
a, ar, ar², ar³ ... arⁿ⁻¹
where, a is the initial term.
r is the common ratio.
According to the question,
The initial term is; a = 2.
The common ratio r = 2.
The threshold value beyond which person start feeling pain is 127.
Thus, last term; arⁿ⁻¹ = 128 (1 feet beyond 127 person start feeling pain)
Last second value is arⁿ⁻².
As, the common ratio is same in GP.
Thus, arⁿ⁻¹ / arⁿ⁻² = ar/a
==> 128/arⁿ⁻² = r
==> 128/arⁿ⁻² = 2
==> 2×2ⁿ⁻² = 64
==> 2ⁿ⁻² = 32
==> n = 7
As, i step is of 2 feet, the total steps taken by the person is 2×7 = 14.
Therefore, the total number of steps beyond which person will feel pain is 14.
To know more about the geometric progression, here
https://brainly.com/question/15978376
#SPJ4
Factor the polynomial by grouping. SELECT EACH FACTOR.
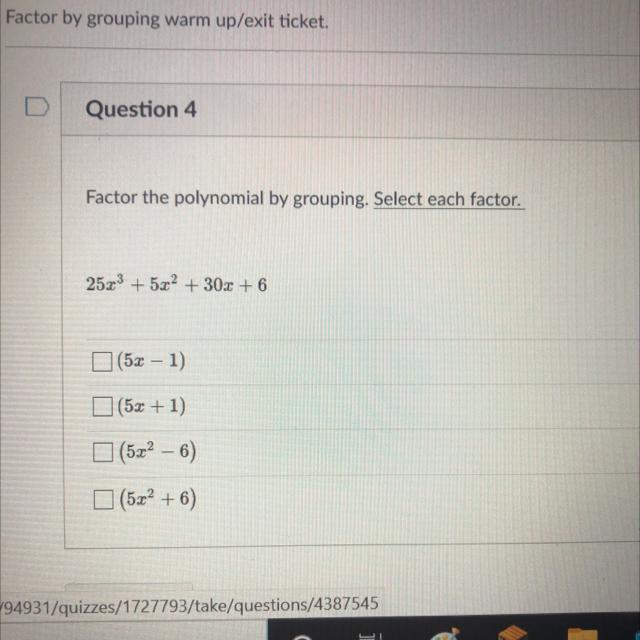
Answers
Answer:
5x+1
5x^2+6
Step-by-step explanation:
What is the value of x?
26°
to
O
X
= [ ? ]
![What is the value of x?26toOX= [ ? ]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/VV2hcYInihaZQ6Zx3k40mRc4bRiPrEjE.png)
Answers
Answer:
154°Step-by-step explanation:
The central angle and the angle between the tangents are supplementary, so
x + 26° = 180° ( subtract 26° from both sides )
26 - 26 = 0
180 - 26 = 154
x = 154°
Answer: 154
Step-by-step explanation: 26 + x = 180, subtract 26 from both sides, x = 154
find the midpoint of the points (3,3) and (-2,-5)
Answers
⇒To find the midpoint use the formula:
⇒\(M(\frac{x_{1}+x_{2} }{2} ,\frac{y_{1} +y_{2} }{2})\\M(\frac{3+(-2)}{2} ,\frac{3+(-5)}{2} )\\\\M(\frac{3-2}{2},\frac{3-5}{2} )\\M(\frac{1}{2} ,\frac{-2}{2} )\\M(\frac{1}{2} ,-1)\)
Your midpoint M is given above .
GOODLUCK!!!
Answer:
Midpoint formula : (\(\frac{x1 + x2}{2}\) , \(\frac{y1 + y2}{2}\))
the given points are (3,3) and (-2,-5).
(3 = x1, 3 = y1) and (-2 = x2, -5 = y2).
we place them in the formula.
(\(\frac{3 + -2}{2}\) , \(\frac{3 + -5}{2}\))
(1/2 , -2/2)
(0.5, -1) is the midpoint.
hope it helps, mark as brainliest :D
Change from rectangular to spherical coordinates. (Let rho≥0,0≤θ≤2π, and 0≤φ≤π.) (a) (0,23,2) (rho,θ,φ)=() (b) (−5,5,56) (rho,θ,φ)=()
Answers
The spherical coordinates for the point (-5, 5, 5/6) are (rho, theta, phi) ≈ (√1825/6, -π/4, 0.387).
(a) To convert the point (0, 2/3, 2) from rectangular coordinates to spherical coordinates, we can use the following formulas: rho = √(x^2 + y^2 + z^2), theta = atan2(y, x), phi = acos(z / rho). In this case, since x = 0, y = 2/3, and z = 2, we have: rho = √(0^2 + (2/3)^2 + 2^2) = √(4/9 + 4) = √(40/9) = 2√10/3, theta = atan2(2/3, 0) = π/2 (since x = 0 and y > 0), phi = acos(2 / (2√10/3)) = acos(3√10/3√10) = acos(1) = 0. Therefore, the spherical coordinates for the point (0, 2/3, 2) are (rho, theta, phi) = (2√10/3, π/2, 0).
(b) To convert the point (-5, 5, 5/6) from rectangular coordinates to spherical coordinates, we can use the same formulas: rho = √(x^2 + y^2 + z^2), theta = atan2(y, x), phi = acos(z / rho). In this case, we have x = -5, y = 5, and z = 5/6: rho = √((-5)^2 + 5^2 + (5/6)^2) = √(25 + 25 + 25/36) = √(900/36 + 900/36 + 25/36) = √(1825/36) = √1825/6, theta = atan2(5, -5) = atan2(-1, 1) = -π/4 (since x < 0 and y > 0), phi = acos(5/6 / (√1825/6)) = acos(5√1825/√1825) = acos(5/√1825) ≈ 0.387
Therefore, the spherical coordinates for the point (-5, 5, 5/6) are (rho, theta, phi) ≈ (√1825/6, -π/4, 0.387).
To learn more about spherical coordinates, click here: brainly.com/question/32587636
#SPJ11
When doing a pull-up, a physics student lifts her 42 kg body to a distance of 0.25 m in 2 seconds. What is the power delivered by the student's biceps?
Answers
The power delivered by the student's biceps is 51.45 watts (W).
To calculate the power delivered by the student's biceps while doing a pull-up, we use the formula:
Power = Work/Time
Since the physics student lifts her 42 kg body to a distance of 0.25 m, the work done is given by:
Work = Force x Distance
The force exerted by the student is equal to her weight, which is given by:
F = mg
where m = 42 kg (mass of the student) and
g = 9.8 m/s² (acceleration due to gravity)
Therefore,
F = 42 kg x 9.8 m/s²
= 411.6 N (weight of the student)
Hence, the work done by the student is:
Work = Force x Distance
= 411.6 N x 0.25 m
= 102.9 J (joules)
The time taken by the student to complete the pull-up is given as 2 seconds.
Therefore:Time = 2 s
Now we can substitute the values into the formula for power:
Power = Work/Time
= 102.9 J/2 s
= 51.45 W
Know more about the work done
https://brainly.com/question/30257290
#SPJ11
(-9) - 9n= (-45) please helpppp!
Answers
Answer: n=4
Step-by-step explanation:
\(\left(-9\right)-9n=\left(-45\right)\)
add 9 to both sides
\(-9-9n+9=-45+9\)
\(-9n=-36\)
divide both sides by -9
\(n=4\)
Brainliest please
━━━━━━━☆☆━━━━━━━
▹ Answer
n = 4
▹ Step-by-Step Explanation
(-9) - 9n = (-45)
Simple terms are written last:
-9 - 9 = -45
Group all the variable terms on one side, and all the constant terms on the other side:
(-9n - 9) + 9 = -45 + 9
n = 4
Hope this helps!
CloutAnswers ❁
━━━━━━━☆☆━━━━━━━
Can someone help me with these questions.
Answers
Answer:
there nothing there
Step-by-step explanation:
Deb has two paintings in her portfolio
and paints three more each week. Kay has
twelve paintings in her portfolio and paints
two more each week. After how many
weeks will Deb and Kay have the same
number of paintings?
Answers
This is basically giving the equation of
3x + 2 = 2x + 12
You would subtract 2x from both sides, and 2 from both sides, and you would get x = 10
What is substitute and example?
Answers
A substitute is a good or service that buyers can quickly swap out for another. For instance, a one-dollar bill can be used in place of another dollar bill.
In business and economics, a replacement, or substitutable good, is a good or service that consumers perceive as just being substantially the same as or reasonably similar to some other good. Consumers are given options and alternatives through substitutes, which also spur competition and lower prices in the market.
Here are a few examples of replacement goods:
1. A $1 bill can be exchanged for four quarters.
2. Coke against Pepsi
3. Regular vs. premium gas
4. Butter and lard
5. Tea and coffee
6. Apples and oranges
7. Comparing driving a car to riding a bike
8. Books in general and e-books
To learn more about substitute link is here
brainly.com/question/18330729
#SPJ4
Enter the mixed number as an improper fraction. 9 1/9 =
Answers
Answer:
82/9
Step-by-step explanation:
To find the improper fraction
Multiply the denominator by the whole number
9*9 = 81
Add the numerator
81+1 = 82
Put it over the denominator
82/9
Answer:
82/9
Step-by-step explanation:
Multiply the whole number part by the fraction's denominator:
9 1/9
9 x 9 = 81
Add the product to the numerator:
81 + 1 = 82
Then write the result on top of the denominator:
82/9
So the answer is 82/9
the boxplot shows the fuel economy ratings for 67 subcompact cars with the same model year. some summary statistics are also provided. the extreme outlier is an electric car whose electricity usage is equivalent to 112 miles per gallon. if that electric car is removed from the data set, how will the standard deviation be affected? the iqr?
Answers
Removing the electric car from the data set will reduce the standard deviation as the extreme value of 112 mpg is taken out, resulting in a decrease in the spread of the data. The interquartile range (IQR) will also be affected as the extreme outlier is taken out, will decrease the spread of the data in the boxplot.
The electric car with a rating equivalent to 112 miles per gallon is an extreme outlier, which means it is very far from the rest of the data. Therefore, removing this outlier from the data set will decrease the variability and, consequently, decrease the standard deviation. The extreme outlier with the rating equivalent to 112 miles per gallon is outside of the whiskers of the boxplot, which means it is beyond the range of the middle 50% of the data. Therefore, removing this outlier from the data set will decrease the spread of the data in the boxplot and, consequently, decrease the IQR.
To know more about standard deviation:
https://brainly.com/question/23907081
#SPJ4
Which of the following represents the polar equation r = (cot 2θ)(csc θ) as a rectangular equation?
x2 + y2 = 1
y = 1
y2 = x3
y3 = x2
Answers
The option that depicts the polar equation r = (cot 2θ)(csc θ) as an equation that is rectangular is: y² = 2x.
A polar expression is any equation that describes the correlation between r and θ, where r signifies the anticlockwise angle formed by a point on a curve, the pole, and the positive x-axis, and means the breadth between the origin and a location on a curve.
What is the solution to the equation above?Step 1 - expand the polar equation
r = 2cosθ * cscθ
Step 2 - convert csc and cos to their equivalents in tan and sin
r = 2 * (1/tanθ) * (1/sinθ) * sinθ
r = 2 * (1/tanθ) * sinθ/sinθ
r = 2 * 1/tanθ
r = 2/tanθ, making 2 the subject of the formula, we have
rtanθ = 2
Note that rectangular coordinates of a point will be depicted as (x,y) and it's plolar coordinate will be (r, θ).
This mean
x = r cos θ; and
y = r sinθ
From the above, we can state that:
Since y = r sinθ
⇒ tanθ = y/x
⇒ (rsinθ/y) * tanθ = 2
Thus y * (y/x) = 2
Therefore,
y²/x = 2
y² = 2x
Learn more about polar equation at:
https://brainly.com/question/9363127
#SPJ1
Can someone please help me with math.

Answers
Answer:
Vertical Angles
Step-by-step explanation:
Hope this helps
2 kg of washing powder for $11.70 or 3 kg for $16.20
Answers
Answer:
3 kg for $16.20
Step-by-step explanation:
If you divide each ($11.70 divided by 2 and $16.20 divided by 3) it will tell you how much each bag costs.
For $11.70, each bag is sold at $5.85
For $16.20, each bag is sold at $5.40
Essentailly, each bag costs less for $16.20
1. Which equation passes through the points (3,-5) and (-1, 3)?
(1) y + 5 = x-3
(2) y = 2x + 1
(3) y-3 = -2(x + 1)
(4) y=x+2
Answers
Answer:
3)y-3=-2(x+1)
Step-by-step explanation:
y-3=-2(x+1)
add 3 on both sides and use distributive property with the -2
y=-2x-2+3
y=-2x+1
graph it.

Answer:
(3) y-3 = -2(x + 1)
Step-by-step explanation:
Lets change all equations to slope-intercept form to easily see the slope.
Slope-Intercept Form:
y = mx+b
M is slope, or the amount the y-value increases when the x-value increases by 1. B is y-intercept, or the y-value of the line when it is intersecting the y-axis (x=0).
#1: y + 5 = x - 3
Subtract 5 on both sides.
y + 5 - 5 = x - 5
Simplify.
y = x - 5
In slope intercept form. Slope of 1 and y-intercept of -5.
#2: y=2x+1
Already in slope intercept form. Slope of 2 and y-intercept of -5.
#3: y-3 = -2(x+1)
Use distributive property to simplify.
y - 3 = -2x-2
Add 3 on both sides.
y - 3 + 3 = -2x - 2 + 3
Simplify.
y = -2x+1
In slope intercept form. Slope of 2 and y-intercept of 1.
#4: y = x+2
Already in slope intercept form. Slope of 1 and y-intercept of 2.
Now using the slope formula, we can eliminate 2 possibilities.
Slope Formula: \(\frac{y_2-y_1}{x_2-x_1}\)
Plug in points.
\(\frac{3--5}{-1-3}\)
Simplify.
\(\frac{8}{-4}\)
Divide.
-2
Slope is -2. Because the slopes of #1 and #4 are 1 (not -2), they cannot be the equation that passes through the line. The slope of #2 is 2, not -2. We are left with: #3.
Which planes contain point W? Select all that apply.
Multiple select question.
cross out
A)
plane B
cross out
B)
plane VWY
cross out
C)
plane VWX
cross out
D)
plane m
cross out
E)
plane RYV
cross out
F)
plane VWZ
Answers
The planes that contain point W from the given image are;
Plane V
Plane VWY
Plane RYV
How to identify planes?A coordinate plane is a graphing and description system for points and lines. A vertical y-axis and a horizontal x-axis make up the coordinate plane.
From the attached image, we see that the planes whose name contains V also contains W.
The plane B contains the line XR and the Line YV as well as the W at the line YV.
Finally, the plane m also contains line YV and obviously the same as plane RYU.
Read more about Planes at; https://brainly.com/question/12227980
#SPJ1

Which of the following could be an example of a function with a domain
(-∞0,00) and a range (-∞,4)? Check all that apply.
A. V = -(0.25)* - 4
-
□ B. V = − (0.25)*+4
c. V = (3)* +4
□ D. V = − (3)* — 4
-

Answers
The correct options that could be an example of a function with a domain (-∞0,00) and a range (-∞,4) are given below.Option A. V = -(0.25)x - 4 Option B. V = − (0.25)x+4
A function can be defined as a special relation where each input has exactly one output. The set of values that a function takes as input is known as the domain of the function. The set of all output values that are obtained by evaluating a function is known as the range of the function.
From the given options, only option A and option B are the functions that satisfy the condition.Both of the options are linear equations and graph of linear equation is always a straight line. By solving both of the given options, we will get the range as (-∞, 4) and domain as (-∞, 0).Hence, the correct options that could be an example of a function with a domain (-∞0,00) and a range (-∞,4) are option A and option B.
Know more about function here:
https://brainly.com/question/11624077
#SPJ8
find the area enclosed by the curve x = t2 − 3t, y = t and the y-axis.
Answers
The area under the curve is \(\frac{6 \sqrt{3}}{5}\).
Consider the following parametric equations:\($$x=t^2-3 t \text { and } y=\sqrt{t} \text { and the } y \text {-axis. }$$\)
The objective is to find area enclosed by the curve using the formula.
The area under the curve is given by parametric equations x=f(t), y=g(t), and is traversed once as t increases from α to β, then the formula for calculating the area under the curve:
\($$A=\int_\alpha^\beta g(t) f^{\prime}(t) d t$$\)
The curve has intersects with y-axis. so x=0
\($$\begin{aligned}t^2-3 t & =0 \\t(t-3) & =0 \\t & =0 \text { or } t=3\end{aligned}$$\)
Now we have to draw the graph,
Let f(t)=\(t^2-3 t, g(t)=\sqrt{t}$\)
Differentiate the curve f(t) with respect to t.
\(f^{\prime}(t)=2 t-3\)
Now, find the area under the curve use the above formula.
\(\begin{aligned}A & =\int_0^3(\sqrt{t})(2 t-3) d t \\& =\int_0^3(2 t \sqrt{t}-3 \sqrt{t}) d t \\& =\int_0^3\left(2 t^{\frac{3}{2}}-3 t^{\frac{1}{2}}\right) d t \\& =\left[2 \frac{t^{\frac{5}{2}}}{\frac{5}{2}}-3 \frac{t^{\frac{3}{2}}}{\frac{3}{2}}\right]_0^3 \\& \left.\left.=\left[\frac{4 t^{\frac{5}{2}}}{5}-2 t^{\frac{3}{2}}\right]_0^3\right]^{\frac{5}{2}}\right] \\\\\end{aligned}$$\)
\(& =\left[\frac{4(3)^{\frac{5}{2}}}{5}-2(3)^{\frac{3}{2}}\right]-\left[\frac{4(0)^{\frac{5}{2}}}{5}-2(0)^{\frac{3}{2}}\right]\)
\($\begin{aligned}& =\left[\frac{4(3)^{\frac{5}{2}}}{5}-2(3)^{\frac{3}{2}}\right]-\left[\frac{4(0)^{\frac{5}{2}}}{5}-2(0)^{\frac{3}{2}}\right] \\& =\frac{4(3)^{\frac{5}{2}}}{5}-2(3)^{\frac{3}{2}}-0 \\& =\frac{6 \sqrt{3}}{5}\end{aligned}\)
Therefore, the area of the curve is \(\frac{6 \sqrt{3}}{5}\).
For more question such on parametric equations
https://brainly.com/question/28537985
#SPJ4

one thousand tickets are sold at $1 each for a smart television valued at $750. what is the expected value of the gain if you purchase one ticket?
Answers
The expected value of the gain if you purchase one ticket is $0.749.
To calculate the expected value of the gain, we need to determine the probability of winning and the amount that can be won.
In this case, there are 1,000 tickets sold and only one television to be won. Therefore, the probability of winning the television is 1/1,000.
The amount that can be won is the value of the television minus the cost of the ticket, which is $750 - $1 = $749.
So, the expected value of the gain can be calculated as follows:
Expected value = probability of winning x amount that can be won
Expected value = (1/1,000) x $749
Expected value = $0.749
Learn more about probability here
brainly.com/question/11234923
#SPJ4
Using integration by parts, rewrite the following integral as fudv = uv-fvdu [in (2x) e 4x² dx
Answers
To rewrite the integral ∫(2x)\(e^{4x^{2} }\)dx using integration by parts, we'll consider the function f(x) = (2x) and g'(x) = \(e^{4x^{2} }\).
Integration by parts states that ∫u dv = uv - ∫v du, where u and v are functions of x.
Let's assign:
u = (2x) => du = 2 dx
dv = \(e^{4x^{2} }\) dx => v = ∫\(e^{4x^{2} }\) dx
To evaluate the integral of v, we need to use a technique called the error function (erf). The integral cannot be expressed in terms of elementary functions. Hence, we'll express the integral as follows:
∫\(e^{4x^{2} }\) dx = √(π/4) × erf(2x)
Now, we can rewrite the integral using integration by parts:
∫(2x)\(e^{4x^{2} }\) dx = uv - ∫v du
= (2x) × (√(π/4) × erf(2x)) - ∫√(π/4) × erf(2x) × 2 dx
= (2x) × (√(π/4) × erf(2x)) - 2√(π/4) × ∫erf(2x) dx
The integral ∫erf(2x) dx can be further simplified using substitution. Let's assign z = 2x, which implies dz = 2 dx. Substituting these values, we get:
∫erf(2x) dx = ∫erf(z) (dz/2) = (1/2) ∫erf(z) dz
Therefore, the final expression becomes:
∫(2x)\(e^{4x^{2} }\) dx = (2x) × (√(π/4) × erf(2x)) - √(π/2) × ∫erf(z) dz
Please note that the integral involving the error function cannot be expressed in terms of elementary functions and requires numerical or tabulated methods for evaluation.
Learn more about integral here:
https://brainly.com/question/31109342
#SPJ11
The tape diagram represents an equation.
Write an equation to represent the image.
(I hope im not asking for too much ;-;)
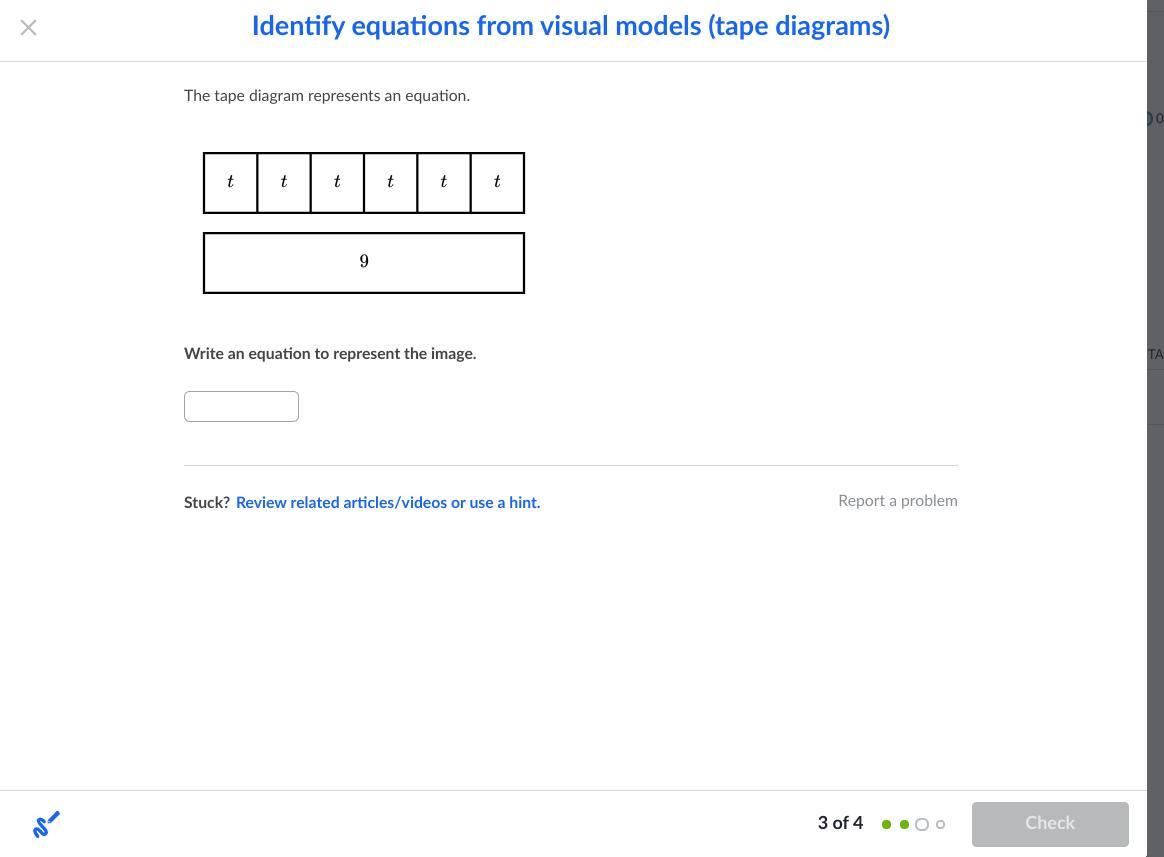
Answers
6t=9
Since the top tape diagram has 6 parts and labeled t (The same size as the bottom diagram), we multiply it, so: 6xt= 6t. 9 is the label of the bottom diagram. That means there are the same or equal to each other.
I hope I've helped!