Answers
Answer:
(5,-3)
Step-by-step explanation:
difference in x is 5 and in y it is .5 so add those to (0,-3.5) and you get (5,-3)
Related Questions
"
A particle is moving according to the position function \( s(t)=(4 t+1)^{3 / 2} \), where \( s(t) \) is measured in centimeters and \( t \) in seconds. Find the acceleration of the particle at \( t=2 seconds. find
"
Answers
The acceleration of the particle at \(t = 2\) seconds is \(4\) cm/s².
To find the acceleration of the particle at \(t = 2\) seconds, we need to differentiate the position function twice with respect to time. First, let's differentiate the position function \(s(t)\) once to find the velocity function \(v(t)\). Using the chain rule, we have:
\(\(v(t) = \frac{d}{dt}[(4t+1)^{3/2}]\)\)
To simplify the differentiation, we can rewrite the function as\(\(v(t) = (4t+1)^{3/2}\)\) . Applying the power rule, the derivative becomes:
\(\(v(t) = \frac{3}{2}(4t+1)^{1/2} \cdot 4\)\)
Simplifying further, we have:
\(\(v(t) = 6(4t+1)^{1/2}\)\)
Next, we differentiate the velocity function \(v(t)\) to find the acceleration function \(a(t)\):
\(\(a(t) = \frac{d}{dt}[6(4t+1)^{1/2}]\)\)
Using the power rule again, we get:
\(\(a(t) = 6 \cdot \frac{1}{2}(4t+1)^{-1/2} \cdot 4\)\)
Simplifying further, we have:
\(\(a(t) = 12(4t+1)^{-1/2}\)\)
Now we can find the acceleration at \(t = 2\) seconds by substituting \(t = 2\) into the acceleration function:
\(\(a(2) = 12(4 \cdot 2 + 1)^{-1/2}\)\)
\(\(a(2) = 12(9)^{-1/2}\)\)
Simplifying the expression, we have:
\(\(a(2) = \frac{12}{3} = 4\) cm/s²\)
Therefore, the acceleration of the particle at \(t = 2\) seconds is \(4\) cm/s².
To know more about acceleration refer here:
https://brainly.com/question/12550364
#SPJ11
A survey indicates that there are approximately 120 dairy farms in a given area. If there are exactly 400 farms, and exactly 20% of them are dairy farms, what is the percent error? Fill in the table below.
Answers
Answer:
a = 120
b = 80
c = 40
d = 0.5
e = 50%
Step-by-step explanation:
Answer:
he is right
Step-by-step explanation:
A survey indicates that there are approximately 120 dairy farms in a given area. If there are exactly 400 farms, and exactly 20% of them are dairy farms, what is the percent error? Fill in the table below.
a =
✔ 120
b =
✔ 80
c =
✔ 40
d =
✔ 0.5
e =
✔ 50%
How do you find the measure of an angle in a triangle isosceles?
Answers
To find the measure of an angle in a triangle that is isosceles, you can use the fact that the two equal sides of the triangle are congruent to each other. The measure of each of these angles can be found by subtracting the measure of the third angle from 180 degrees.
Determine which two sides of the triangle are equal in length (these are called the "congruent sides").
Find the measure of the angle opposite one of the congruent sides. This angle is called the "base angle."
Subtract the measure of the base angle from 180 degrees. This will give you the measure of the other two angles in the triangle (since the three angles in any triangle must add up to 180 degrees).
For example, if the measure of the base angle is x degrees, then the measure of the other two angles would be (180-x) degrees.
To know more about triangle click below:
https://brainly.com/question/2773823#
#SPJ4
The measure of angles in an isosceles triangle can be found using the Triangle Angle Sum Theorem. This theorem states that the sum of the angles in any triangle is 180 degrees. Therefore, if you know two of the angles in the triangle, you can find the third angle by subtracting the sum of the two known angles from 180.
To find the measure of an angle in a triangle isosceles, you can use the Triangle Angle Sum Theorem. This theorem states that the sum of the angles in any triangle is 180 degrees. Therefore, if you know two of the angles in the triangle, you can find the third angle by subtracting the sum of the two known angles from 180.
Let's look at an example. Suppose you have an isosceles triangle and you know that two of its angles measure 50 degrees and 60 degrees. To find the measure of the third angle, you would subtract 110 (the sum of the two known angles) from 180. This gives you 70 degrees as the measure of the third angle.
In addition to the Triangle Angle Sum Theorem, you can also use the Isosceles Triangle Theorem to find the measure of an angle in an isosceles triangle. The Isosceles Triangle Theorem states that the angles opposite the two equal sides of an isosceles triangle are equal. This means that if you know one of the angles in the triangle, you can determine the measure of the other two angles, since they will both be equal to the measure of the known angle.
Learn more about isosceles triangle here
https://brainly.com/question/2456591
#SPJ4
use a linear approximation (or differentials) to estimate the given number. 3 root 65
Answers
The estimate for 3√65 is 49/12.
How to use a linear approximation?To use a linear approximation (or differentials) to estimate the given number 3√65, follow these steps:
1. Choose a number close to 65 that has an easy-to-calculate cube root, such as 64 (since the cube root of 64 is 4).
2. Define the function f(x) = 3√x.
3. Calculate the derivative f'(x) = (1/3)x^(-2/3).
4. Evaluate f'(x) at the chosen number (x=64): f'(64) = (1/3)(64)^(-2/3) = 1/12.
5. Apply the linear approximation formula: Δy ≈ f'(x)Δx, where Δy is the change in f(x) and Δx is the change in x.
6. Find the change in x (Δx): Δx = 65 - 64 = 1.
7. Calculate the change in y (Δy): Δy ≈ f'(64)Δx = (1/12)(1) = 1/12.
8. Add the change in y (Δy) to the initial function value f(64): 3√65 ≈ 3√64 + Δy = 4 + 1/12 = 49/12.
So, using linear approximation, the estimate for 3√65 is 49/12.
Learn more about linear approximation
brainly.com/question/1621850
#SPJ11
Completely factor the polynomial. 12x2 2x - 4 2(3 x 2)(2 x - 1) (3 x 2)(4 x - 2) 2(6 x2 2 x - 1) (6 x 4)(2 x - 1)
Answers
The completely factored form of the polynomial is :\(\(12x^2 + 2x - 4 = 2(2x + 4)(3x - 1)\)\)
To completely factor the polynomial \(\(12x^2 + 2x - 4\)\), we need to find expressions that can be multiplied together to obtain the given polynomial.
First, we can look for common factors. In this case, all the coefficients are divisible by 2, so we can factor out a 2:
\(\(2(6x^2 + x - 2)\)\)
Now, we focus on factoring the quadratic expression \(\(6x^2 + x - 2\)\). We need to find two binomials that, when multiplied, give us this quadratic.
To factor \(\(6x^2 + x - 2\)\), we look for two numbers whose product is equal to \(\(6 \times -2 = -12\)\) and whose sum is equal to the coefficient of the middle term, which is 1.
After trying different combinations, we find that the numbers 4 and -3 satisfy these conditions:
\(\(6x^2 + x - 2 = (2x + 4)(3x - 1)\)\)
Putting it all together, the completely factored form of the polynomial is:
\(\(12x^2 + 2x - 4 = 2(2x + 4)(3x - 1)\)\)
To know more about polynomial visit -
brainly.com/question/32838567
#SPJ11
Write an equation to represent the following statement.
j divided by 9 is 5.
solve for j.
j=

Answers
Answer: j = 45
Find the equation of the line of best fit for the points ( − 4 , 10 ) , ( − 1 , 5 ) , ( 2 , − 1 ) , ( 3 , − 6 ) , and ( 5 , − 7 ) .
Answers
The equation of the line of best fit for the points is y = -2x + 3
Equation of line of best fitThe distance between two points is referred to as a line. The standard equation of a line in slope-intercept form is expressed according to the equation
y = mx + b
where:
m is the slope
b is the intercept
Using the coordinate points (-1, 5) and. (5, -7)
Slope = -7-5/5-(-1)
Slope = -12/6
Slope = -2
Find the y-intercept
-7 = -2(5) + b
-7 = -10 + b
b. = 3
Determine the equation
y = mx + b
y = -2x + 3
This gives the required equation of line of best fit.
Learn more on line of best fit here: https://brainly.com/question/17013321
#SPJ1
When Sophia's mom picks her up from
school, she is late one third of the time. For
the next 15 days, what is the probability
that she will be late at most three days?
Answers
Answer:
20.92 %.
Step-by-step explanation:
Add the individual probability of 0, 1, 2, and 3 late days out of 15
P(0 days) = (2/3)15 Notice that I have made P the probability of NOT being late.
P(1 day) = 15(2/3)14(1/3)
Hope this helps!
I need to find out what the answer to m is
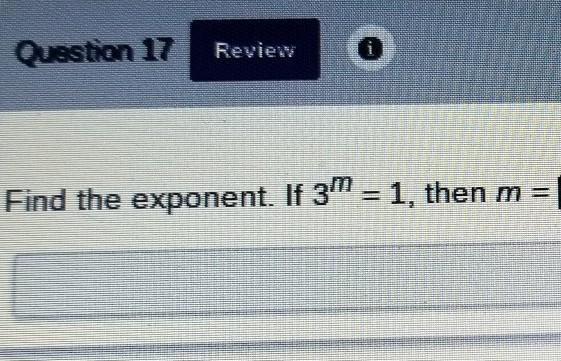
Answers
Answer:
m=0
Step-by-step explanation:
3^0=1
Answer:
Step-by-step explanation:
ok
(GIVING BRAINLIEST!!!!!!!!!)
Read the following quotation from the Constitution. "We the People of the United States, in Order to form a more perfect Union, establish Justice, insure domestic Tranquility. . . .do ordain and establish this Constitution for the United States of America." Which of the following describes the purpose of the paragraph?
A) To explain why the United States wanted to declare independence from Britain
B) To describe the goal of the writers in creating the Constitution
C) To explain which rights the Constitution will protect
D) To describe who is responsible for writing the document
Answers
Answer:
B
Step-by-step explanation:
Sorry for late response just saw your other comment. Also good luck
Answer:
B.
Step-by-step explanation:
To describe the goal of the writers in creating the constitution
The rubber track for a toy digger goes around four circular wheels of diameter 8 cm, as shown. (b) Calculate the length of the rubber track that goes around the four wheels. Give your answer correct to one decimal place.
Answers
Answer:
73.1 cm
Step-by-step explanation:
In the drawing, the rubber track is in black and the wheels are in light gray.
As we can see in the figure, the rubber track will have a length of two halfs of a circunference of radius 8 cm plus six diameters of 8 cm. So the total length is:
Length of rubber track = pi * 8 + 6 * 8 = 25.13 + 48 = 73.133 cm
Rounding to one decimal place, we have that the length is 73.1 cm

This question is incomplete because it lacks the diagram of the 4 circular wheels.
Find attached to this answer the appropriate diagram
Answer:
100.5cm
Step-by-step explanation:
The formula to be used in this calculation is the circumference of a circle.
The circumference of a circle can be defined as the actual length of a circle when it is stretch out(opened up) or the distance around a circle.
The formula for the circumference of a circle is given as 2πr where r = radius of the circle
Or πD where D = Diameter of the circle
In the question, we are given the diameter of the circle = 8cm
So we use the Formula
= πD
The length of the rubber track around one wheel is
= π × 8cm = 25.132741229cm
From the attached diagram, we can see we have 4 wheels.
The length of the rubber track that goes around the four wheels is calculated as
4 × 25.132741229cm = 100.53096491cm.
Approximately to one decimal place = 100.5cm
Therefore, the length of the rubber track that goes around the four wheels to one decimal place is 100.5cm

Donna bought 3 bags of dog treats for $6.93. What is the cost per bag of dog treats?
Answers
Answer:$20.79
Step-by-step explanation:
question (b) please. Thank you

Answers
first we will open bracket by squaring all the digits, then we will take LCM of the denominators and write in the standard form, it cant be further solved

Answer:
x²/9 - x/6 + 1/16
Step-by-step explanation:
Using (a - b)² = a² - 2ab + b, expand the expression:
x²/9 - 2x/12 + 1/16
reduce the fraction with two:
x²/9 - x/6 + 1/16
and you're done!
Evaluate ∬ ydA,D is the triangular region with vertices (0,0), (1,1), and (4,0)
D
Answers
The limits of integration for x will be from x = 0 to x = 4.
We can now evaluate the integral as follows:
∫∫ y dA,
\(D = \int 0^4 \int0^{(1-(1/4)x)}\ y\ dy\ dx\)
\(= \int0^4 [y^2/2]0^{(1-(1/4)x)} dx\)
= ∫0⁴ [(1/2)(1-(1/4)x)²] dx
= (1/2) ∫0⁴ (1- (1/2)x + (1/16)x²) dx
= (1/2) [(x-(1/4)x²+(1/48)x^3)]0⁴
= (1/2) [(4-(1/4)(16)+(1/48)(64))-0]
= (1/2) (4-4+4/3)
= 2/3
Therefore, ∬ ydA = 2/3.
To evaluate ∬ ydA,
we need to integrate the function y over the region D.
The region D is a triangular region with vertices (0,0), (1,1), and (4,0). Therefore, we can evaluate the integral as follows:
∬ ydA = ∫∫ y dA, D
The limits of integration for y will depend on the limits of x for the triangular region D.
To find the limits of integration for x and y, we need to consider the two sides of the triangle that are defined by the equations y = 0 and
y = 1 - (1/4)x.
The limits of integration for y will be from y = 0 to y = 1 - (1/4)x.
To know more about integration, visit:
https://brainly.com/question/31744185
#SPJ11
sandy had five -dollar bill,2 one dollar bills,5 quarters ,and 6 nickels .she gave $1.30 to the vacation Bible school offering .how much did she have left?
Answers
find f · dr c for the given f and c. f = x2 i y2 j and c is the line from the point (2, 5) to the point (4, 7).
Answers
The value of the line integral f · dr over the curve C is 20 i + 39 j.
How to find f · dr c for the given f and c ?Let's first find a parameterization of the line from the point (2,5) to the point (4,7). We can choose t as the parameter and write the parameterization as:
x = 2 + 2t
y = 5 + 2t
where 0 ≤ t ≤ 1.
Next, we need to evaluate f · dr along this curve C. Substituting the parameterization into f · dr, we get:
\(f · dr = (x^2 i + y^2 j) · (dx i + dy j)\)
\(= x^2 dx + y^2 dy\)
\(= (2 + 2t)^2 dt i + (5 + 2t)^2 dt j\)
\(= (4t^2 + 8t + 4) dt i + (4t^2 + 20t + 25) dt j\)
Finally, we integrate f · dr over the range of t from 0 to 1 to get the line integral:
f · dr C = ∫(0 to 1) (\(4t^2\) + 8t + 4) dt i + ∫(0 to 1) (\(4t^2\) + 20t + 25) dt j
=\([4/3t^3 + 4t^2 + 4t]\) from 0 to 1 i + \([4/3t^3 + 10t^2 + 25t]\) from 0 to 1 j
= \((4/3 + 4 + 4) i + (4/3 + 10 + 25) j\)
= \(20 i + 39 j\)
Therefore, the value of the line integral f · dr over the curve C is 20 i + 39 j.
Learn more about line integrals
brainly.com/question/31013115
#SPJ11
Solve the quadratic equation.
x² + 9x - 36 = 0
O A. x = 3 or 12
OB. x = 3 or -12
O C. x = 6 or -6
OD. no real solution
Answers
Answer:
B x = 3 or -12
Step-by-step explanation:
(btw this / is a fraction sign and this ^ is the power of sign)
Let's solve your equation step-by-step.
x^2+9x−36=0
For this equation: a=1, b=9, c=-36
1x^2+9x+−36=0
Step 1: Use quadratic formula with a=1, b=9, c=-36.
x= −b±√b^2−4ac/2a
x= −(9)±√(9)2−4(1)(−36)/2(1)
x= −9±√225/2
= x= 3 or x= -12
A. -5
B.-1/5
C.1/5
D.5

Answers
Answer:
b
Step-by-step explanation:
A salesman sells a car for 960,000.If he receives a commission of 15%,how much will be his commission?
Answers
Answer:
144 000
Step-by-step explanation:
960 000 × 0.15
= 144 000
Answer:
144,000
Step-by-step explanation:
\( \frac{15}{100} \times 960000 \\ 15 \times 9600 \\ 144000\)
Solve the system of equations:
y= 2x - 2
y= x2 - x-6
O A. (-1,-5) and (4,2)
O B. (0, -2) and (2, 2)
O C. (-1,-4) and (4, 6)
D. (-2,0) and (3,0)
Answers
Answer:
C) (-1, -4) and (4, 6)
Step-by-step explanation:
\(\textsf{Equation 1}:y=2x-2\)
\(\textsf{Equation 2}:y=x^2-x-6\)
Substitute Equation 1 into Equation 2 and solve for x:
\(\implies 2x-2=x^2-x-6\)
\(\implies x^2-3x-4=0\)
Find two numbers that multiply to -4 and sum to -3: -4 and 1
Rewrite the middle term as the sum of these two numbers:
\(\implies x^2-4x+x-4=0\)
Factorize the first two terms and the last two terms separately:
\(\implies x(x-4)+1(x-4)=0\)
Factor out the common term \((x-4)\):
\(\implies (x+1)(x-4)=0\)
\(\implies (x+1)=0 \implies x=-1\)
\(\implies (x-4)=0 \implies x=4\)
Substitute the found values of x into Equation 1 and solve for y:
\(x=-1 \implies y=2(-1)-2=-4\)
\(x=4 \implies y=2(4)-2=6\)
Therefore, the solution to the system of equations is:
(-1, -4) and (4, 6)
using Matlab
Find the inverse Laplace of the following function using the partial fraction expansion coefficients from the MATLAB. \[ G(s)=\frac{2 s^{3}+5 s^{2}+3 s+6}{s^{3}+6 s^{2}+11 s+6} \] Show you calculation
Answers
The inverse Laplace transform of G(s) is:
g(t) = (2/3) \(e^{-t}\) - (1/3) \(e^{-2t}\) - (1/3) \(e^{-3t}\)
The inverse Laplace transform of the function G(s) using the partial fraction expansion coefficients obtained from MATLAB, we need to express G(s) in terms of partial fractions.
G(s) = (2s³ + 5s² + 3s + 6) / (s³ + 6s² + 11s + 6)
The denominator of G(s) can be factored as:
s³ + 6s² + 11s + 6 = (s + 1)(s + 2)(s + 3)
Let's write G(s) in terms of partial fractions as follows:
G(s) = A / (s + 1) + B / (s + 2) + C / (s + 3)
To find the values of A, B, and C, we can multiply both sides of the equation by the denominator and equate the coefficients of like powers of s.
(2s³ + 5s² + 3s + 6) = A(s + 2)(s + 3) + B(s + 1)(s + 3) + C(s + 1)(s + 2)
Expanding the right side and collecting like terms, we have:
2s³ + 5s² + 3s + 6 = (A + B + C)s² + (5A + 4B + 3C)s + (6A + 3B + 2C)
Comparing the coefficients of like powers of s, we get the following equations:
A + B + C = 0
5A + 4B + 3C = 5
6A + 3B + 2C = 3
Solving these equations, we find:
A = 2/3
B = -1/3
C = -1/3
Therefore, the partial fraction expansion of G(s) becomes:
G(s) = (2/3) / (s + 1) - (1/3) / (s + 2) - (1/3) / (s + 3)
Now, we can use the linearity property and known Laplace transforms to find the inverse Laplace transform of each term.
Taking the inverse Laplace transform, we have:
g(t) = (2/3) \(e^{-t}\) - (1/3) \(e^{-2t}\) - (1/3) \(e^{-3t}\)
Therefore, the inverse Laplace transform of G(s) is:
g(t) = (2/3) \(e^{-t}\) - (1/3) \(e^{-2t}\) - (1/3) \(e^{-3t}\)
To know more about inverse Laplace transform click here :
https://brainly.com/question/32705640
#SPJ4
so lets say you have to do 257+102+51+41 which is 451 right?
so what would it be if someone took 30% of that 451 like tax what would you be left with? first person to answer CORRECTLY ill give u thanks
Answers
First we are supposed to find 30% of 451
30/100×451 = 135.3
So, 451 - 136= 315.7
Therefore I would be left with 315.7
Answer:
$315.70
Step-by-step explanation:
the sum of these is 451 so to find 30 percent we multiply 451 by 30 percent
First turn 30 percent into a decimal by moving the decimal point to places to the left
0.30 and now we multiply
0.3x451
135.30 is 30% of 451 and since someone is taking it we subtract it by 451
451-135.30
315.70 is what you are left with
But if it was tax you would add this to the total amount you are spending
Hopes this helps please mark brainliest
A shopkeeper sold an article for Birr 280. If its cost price is Birr 350 then what is his loss percentage?
Answers
Answer:
percentage loss = 20%
Step-by-step explanation:
percentage loss is calculated as
\(\frac{loss}{CP}\) × 100% ( CP is the cost price )
loss = SP - CP ( SP is selling price )
loss = CP - SP = 350 - 280 = 70 , then
percentage loss = \(\frac{70}{350}\) × 100% = 0.2 × 100% = 20%
Imagine two line segments where each represents a slant height of the cone. The segments are on opposite sides of the cone and meet at the apex. Find the measurement of the angle formed between the line segments.

Answers
To determine the slant height of the cone, we will apply the Pythagorean theorem to the right triangle ABC.
From the Pythagorean theorem we get that:
\(AC^2=AB^2+BC^2.\)We are given that:
\(\begin{gathered} BC=6in, \\ AB=\frac{4in}{2}=2in. \end{gathered}\)Therefore:
\(AC^2=(6in)^2+(2in)^2=36in^2+4in^2.\)Finally, solving for AC, we get:
\(AC=\sqrt{40in^2}=2\sqrt{10}\text{ in.}\)Answer: \(\begin{equation*} 2\sqrt{10}\text{ in.} \end{equation*}\)5. What is the value of s if 8.25s - 2.375 = 10?
1.5
8,25
8
1.7
8,25
06
8,25
093
Answers
Answer:
1
Step-by-step explanation:
8-1,2,4.....
25-1,5...
Please help!! Thank you!!

Answers
Answer: x>-1
Step-by-step explanation:
Dotted line on the axis is covering y infinitely, so theres an inequality on x, and the line is at -1, so x should be > - 1
Answer:
C. x > -1
Step-by-step explanation:
The line intersects on the x-axis at -1 and is shaded towards the right, which are all numbers greater than -1. The inequality that matches this is x > -1.
If the variable was y, then the line would be horizontal on the y-axis. If the inequality was x > 1, then the line would intersect on the x-axis on positive 1. This is why the other options are incorrect.
hope this helps!
helpppppppppp anyone know algebra?

Answers
Answer:
5x/7y^3
Step-by-step explanation:
Something to the power of -1/2 is saying 1 over square-root of that something. Let's pretend x is that something. If we have something like this \(x^{-\frac{1}{2} }\), then it can be written like this: \(\frac{1}{\sqrt{x}}\).
In our problem, we have the chunk to the -1/2 power. So the reciprocal of the chunk would become \(\sqrt{\frac{25x^{2} }{49y^{6}}\)
It's easy to solve now. The square root of the numerator becomes 5x and the denominator becomes 7y^3. The simplified version is \(\frac{5x}{7y^\power{3}}\)
4 – 2( x – 3 ) = 2 4
Answers
Answer:
-7
Step-by-step explanation:
Answer:
x=-7
Step-by-step explanation:
:)
Perform the indicated operation, and write the answer in lowest terms.
−16/5 ⋅ (−15/56)
Answers
Answer:
6/7
Step-by-step explanation:
First, cancel out 16 and 56 by a common factor of 8. The resulting expression is -2/5*-15/7. Then, simply 5 and 15 by a common factor of 5. Then, you will get: -2*(-3/7). The negatives cancel out, so the answer is 6/7.
36 = 4x
Thank you | (• ◡•)|
Answers
Answer:
x = 9
Step-by-step explanation:
