The ordered pair given in the bottom row can be written using function notation as

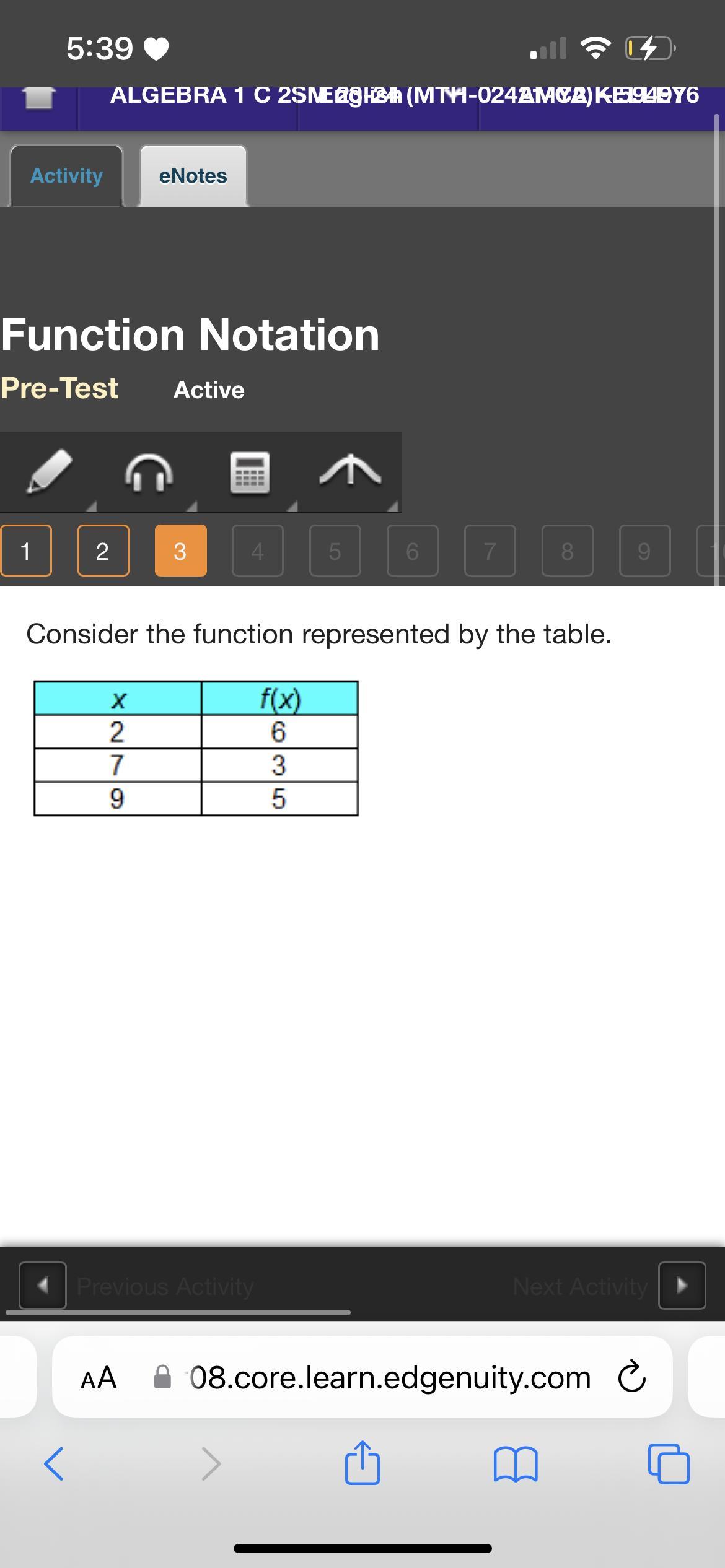
Answers
Using function notation, the ordered pair (x, y) in the bottom row can be written as y = f(x), where f represents the function relating the input x to the output y.
To write the ordered pair given in the bottom row using function notation, we need to assign variables to the elements of the ordered pair. Let's assume the ordered pair is (x, y).
The function notation represents the relationship between x and y. The x value corresponds to the input or independent variable, and the y value corresponds to the output or dependent variable.
In function notation, we can write the ordered pair as y = f(x), where f represents the function.
For example, if the ordered pair is (3, 5), we can write it as y = f(3), indicating that the output y is a function of the input x, which is 3.
For more such questions on function
https://brainly.com/question/11624077
#SPJ8
Related Questions
-78 divided by (-1.3)
Answers
Answer:
60
Step-by-step explanation:

Solve following equations by reducing their augmented matrix to the reduced echelon form
x+2y+z=2
2x+y+2z= -1
2x+3y-z = 9
Answers
Answer:
Step-by-step explanation:
it is actually in the textbook pg 119

The length of time for one individual to be served at a cafeteria is a random variable having an exponential distribution with a mean of 4 minutes. What is the probability that a person is served in less than 3 minutes
Answers
The probability that a person is served in less than 3 minutes at the cafeteria can be calculated using the exponential distribution with a mean of 4 minutes. The answer is approximately 0.5507.
To calculate this probability, we can use the cumulative distribution function (CDF) of the exponential distribution. The CDF gives us the probability that the random variable takes on a value less than or equal to a given value. In this case, we want to find the probability that the serving time is less than 3 minutes.
The CDF of the exponential distribution is given by the formula:
CDF(x) = 1 - e^(-λx)
Where λ is the rate parameter of the exponential distribution, which is equal to 1 divided by the mean. In this case, the mean is 4 minutes, so λ = 1/4.
Plugging in the values into the formula, we have:
CDF(3) = 1 - e^(-(1/4) * 3)
≈ 1 - e^(-3/4)
≈ 1 - 0.4724
≈ 0.5276
Therefore, the probability that a person is served in less than 3 minutes is approximately 0.5507.
To know more about exponential distribution, refer here:
https://brainly.com/question/30669822#
#SPJ11
The length of the rectangle below is
(2x-3) and the width is (x+7). Find the
area of the rectangle in terms of x.
Answers
Step-by-step explanation:
\(area \: of \: rectangle \: = \: length \: \times width \\ area = (2x - 3) \times (x + 7) \\ = 2 {x}^{2} + 14x - 3x - 21 \\ = 2 {x}^{2} + 11x - 21\)
Please help me with this question it is in the picture

Answers
Answer:
complementary angles
Step-by-step explanation:
The sum of the angles is 67+23 = 90
When angles sum together to 90, the are called complementary
Answer:
Option A
Step-by-step explanation:
The measures of the two angles have a sum of 90°.
\(67+23=90\)
Therefore, they are complementary angles, since complementary angles have a total measure of 90°.
Option A is the best answer.
Brainilest Appreciated.
A square tile has a width of 1 foot. How many tiles will fit end-to-end along a
4-foot wall?
Answers
Explanation: if the square has a width of one foot then the length is also one foot since all sides are equal. Therefore 4 squares can fit along a 4 foot wall
Answer:
4
Step-by-step explanation:
Starting at the left end of the wall, you'll find that you can set four (4) tiles end to end along this wall.
The Leungs sold a valuable painting for $55,000. This price is $1,000
more than twice the amount they originally paid for it. How much
did they originally pay?
A. $25,000 B. $27,000 C. $27,500 D. $28,000
Answers
Answer:
B. $27,000
Step-by-step explanation:
So 55,000 = 2x + 1,000
Simply for x
55,000 = 2x + 1,000
54,000 = 2x
x = 27,000
f(x) = 4x^2 - 7x + 7 find f(7)
Answers
Answer:
ummmm what grade do you are
Answer:
f(7)=140
Step-by-step explanations:
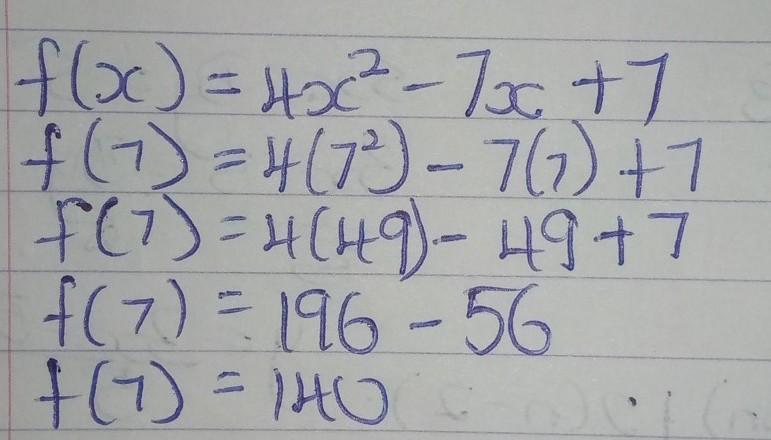
What is the solution to this system of linear equations XY 6 and Y x =- 10?
Answers
The solution to this system of linear equations y - x = 6 and y + x = -10 is (-8, -2).
y - x = 6
⇒y = x + 6
y + x = -10
⇒y = - x - 10
Since both equations are equal to y, equate them.
x + 6 = - x - 10
x + x = - 10 - 6
2x = - 16
Divide both sides by 2
x = -8
Put the value of x in either of the equations
y - x = 6
y - (-8) = 6
y + 8 = 6
y = 6 - 8
y = - 2
Therefore, the solution to the system of linear equations is (-8, -2).
To know more about linear equations, here
https://brainly.com/question/12974594
#SPJ4
Given the differential equation dy/dx = -2x/y^2, find the particular solution, y = f(x), with the initial condition f(3) = -3
Answers
The particular solution to the differential equation dy/dx = \(-2x/y^2\) with the initial condition f(3) = -3 is y = f(x) = \((-3x^2)^{(1/3)}.\)
To find the particular solution of the differential equation dy/dx = \(-2x/y^2\) with the initial condition f(3) = -3, we need to use separation of variables method.
First, we can rewrite the equation as \(y^2dy\) = -2xdx.
Next, we can integrate both sides: ∫\(y^2dy\) = -∫2xdx.
This gives us the equation \((1/3)y^3 = -x^2 + C\), where C is the constant of integration.
To find the value of C, we can use the initial condition f(3) = -3. Substituting x = 3 and y = -3, we get:
\((1/3)(-3)^3 = -(3)^2 + C\)
-9 = -9 + C
C = 0
Therefore, the particular solution to the differential equation dy/dx = \(-2x/y^2\) with the initial condition f(3) = -3 is given by:
\((1/3)y^3 = -x^2\)
\(y^3 = -3x^2\)
\(y = (-3x^2)^{(1/3)\)
So, the particular solution is y = f(x) = \((-3x^2)^{(1/3)}.\)
To know more about differential equation, refer to the link below:
https://brainly.com/question/31583235#
#SPJ11
A fencing compony charges $22 per foot to install
a wood fence. How much will it cost to install a
wood fence around a rectangular pool area that is
20 feet wide and 38 feet long?
Answers
A box has the shape of a rectangular prism with height 30 cm. If the height is increased by 0.2 cm, by how much does the surface area of the box increase?
Answers
If the height is increased by 0.2 then the surface area will be increased by 1.14times the original.
What is surface area of a prism?A prism is a solid shape that is bound on all its sides by plane faces.
The surface area of a prism is expressed as;
SA = 2B + ph
where h is the height , p is the perimeter of the base and B is the base area
The scale factor in terms of height = 32/30
if x is the surface area of old prism and y for new
then area factor = (16/15)² = 256/225
256/225 = y/x
225y = 256x
y = 256/225 x
y = 1.14x
therefore the surface area will increase by 1.14times the original.
learn more about surface area from
https://brainly.com/question/16519513
#SPJ1
Given the equation y= 2x - 8, what is the slope and the y-intercept?
Om = 2 and b= 8
O m= 2 and b= -8
m= 8 and b=2
O m= -8 and b= 2
Answers
mx+b !!
a penny is thrown from the top of a 52.6-meter building and hits the ground 3.31 seconds after it was thrown. the penny reached its maximum height above the ground 0.85 seconds after it was thrown. define a quadratic function, h , that expresses the height of the penny above the ground (measured in meters) as a function of the number of seconds elapsed since the penny was thrown, t.
Answers
The quadratic function which models the motion of the penny is
h(t) = -4.9t² -0.327761 t + 52.6
and the maximum height reached is 57.43
h(t) = - 0.5gt² + vt + h
g = 9.8 m/s²
h = 52.6 m
v = ?
For v,
h(t) = -0.5gt² + vt + 52.6
h(t) = - 4.9t² + vt + 52.6
Time when penny hits the ground ; t = 3.31
h(3.31) = 0
0 = -4.9(3.31)² + v(3.31) + 52.6
0 = -53.68489 + 3.31v +52.6
3.31v = -1.08489
v = -1.08489/3.31
v = -0.327761 m/s
Therefore,
h(t) = -4.9t² -0.327761 t + 52.6
2.) Maximum height of the penny above the ground
t = 0.85 seconds
h(0.85) = -4.9(0.85^2)-0.327761 (0.85) + 52.6
Maximum height reached = 57.43 meters
Therefore, the maximum height reached is 57.43 meters.
An object changing its position with regard to time is referred to as motion. Motion is mathematically characterised in terms of displacement, distance, velocity, acceleration, and speed as well as the observer's frame of reference and the measurement of the change in the body's position with respect to that frame over time. Kinematics is the area of physics that studies how motion is affected by forces, whereas dynamics is the area that studies how motion is affected by forces.
To learn more about motions
https://brainly.com/question/18980389
#SPJ4
If you have a right triangle with 36 square units. what is the scaled value if you go 2-1 , 3-1?
Answers
Answer:
324, 900, 9
Step-by-step explanation:
When a shape has its size increased by a scale factor, the size of its lengths are multiplied by this scale factor, yet its area is actually multiplied by the scale factor squared. This is due to two lengths being multiplied to contribute to the area, not just one. If it was a volume, you would multiply by the scale factor cubed!
Onto the answer, just follow the advice above:
36 * 3^2 = 36 * 9 = 324 square inches,
36 * 5^2 = 36 * 25 = 900 square inches,
36 * 0.5^2 = 36 * 0.25 = 9 square inches.
Hope this helps :)
Doctor Specialties Below are listed the numbers of doctors in various specialties by gender.
Pediatrics Psychiatry Pathology
Male 12,575 33,020 27,803
Female  5,604 33,351 12,292
Required:
a. Find P (male|pediatrician).
b. Find P (pathologist)female).
c. Are the characteristics "female" and "pathologist" independent?
Answers
The respective conditional probabilities are;
A) P(Male|pediatrician) = 0.6917
B) P(pathologist|female) = 0.24
C) No they are not independent
What is Conditional Probability?
A) We want to find P(Male|pediatrician)
This means probability that it is a male that is selected given that it is a pediatrician.
Total pediatricians = 12575 + 5604 = 18179
Thus;
P(Male|pediatrician) = 12575/18179
P(Male|pediatrician) = 0.6917
B) Find P(pathologist|female).
This means probability that it is a pathologist and given that it is a female.
Total number of females = 5604 + 33351 + 12292 = 51247
Thus;
P(pathologist|female) = 12292/51247
P(pathologist|female) = 0.24
C) From the answers above, female and pathologist are not independent.
Read more about conditional probability at; https://brainly.com/question/23382435
What is the ratio of the surface areas of the similar square pyramids below?

Answers
Step-by-step explanation:
8 times 12 is 96
10 times 15 is 150 add them together and get 246
Suppose that n balls are tossed into n bins, where each toss is independent and the ball is equally likely to end up in any bin. What is the expected number of empty bins
Answers
The expected number of empty bins when tossing n balls into n bins, with each toss being independent and equally likely, can be determined using the concept of probability.
Let's define the probability that a specific bin remains empty after n tosses as P(empty). Since each ball has n choices, there are n^n possible ways to distribute the balls. To find the probability that a specific bin is empty, we can consider the situation where balls can be tossed into the remaining n-1 bins, resulting in (n-1)^n possible distributions. Therefore, P(empty) = ((n-1)^n) / (n^n).
Now, to calculate the expected number of empty bins, we can use the concept of linearity of expectation. The expected value of the sum of random variables is equal to the sum of the expected values of the individual random variables. In this case, the random variables represent the empty status of each bin (1 if empty, 0 if not).
The expected number of empty bins is the sum of the probabilities of each bin being empty, which is n * P(empty). So, the expected number of empty bins = n * (((n-1)^n) / (n^n)).
Using this formula, you can determine the expected number of empty bins when n balls are tossed into n bins independently and with equal likelihood.
Learn more about independent here:
https://brainly.com/question/15375461
#SPJ11
Find the area under the standard normal curve to the left of z=2.06. round your answer to four decimal places.
Answers
The area under the standard normal curve to the left of z = 2.06 is approximately 0.9803.
The normal distribution function, also known as the Gaussian distribution or bell curve, is a probability distribution that is symmetric, bell-shaped, and continuous. It is defined by two parameters: the mean (μ) and the standard deviation (σ).
The normal distribution is widely used in statistics and probability theory due to its many desirable properties and its applicability to various natural phenomena. It serves as a fundamental distribution for many statistical methods, hypothesis testing, confidence intervals, and modeling real-world phenomena.
To find the area under the standard normal curve to the left of z = 2.06, you can use a standard normal distribution table or a calculator with a normal distribution function. The standard normal distribution is a normal distribution with a mean of 0 and a standard deviation of 1.
Using a standard normal distribution table, the area to the left of z = 2.06 can be found by looking up the corresponding value in the table. However, since the standard normal distribution table typically provides values for z-scores up to 3.49, we can approximate the area using the available values.
The closest value in the standard normal distribution table to 2.06 is 2.05. The corresponding area to the left of z = 2.05 is 0.9798. This means that approximately 97.98% of the area under the standard normal curve lies to the left of z = 2.05.
Since z = 2.06 is slightly larger than 2.05, the area to the left of z = 2.06 will be slightly larger than 0.9798.
Therefore, rounding the answer to four decimal places, the area under the standard normal curve to the left of z = 2.06 is approximately 0.9803.
To know more about function visit:
https://brainly.com/question/31062578
#SPJ11
in the market for canadian dollars measured in us dollars, if the price of a us dollar is 1.10 canadian dollars, a canadian dollar is a.1.10 us dollars b.1 us dollar c.0.99 cents us d.0.91 cents us
Answers
The price of one canadian dollar in US dollars is 91 cents or 0.91 US dollars.
It is given that the price of a US dollar is 1.10 Canadian dollars in the market.
Thus we can say that,
1.10 Canadian Dollar = 1 US Dollar
∴ 1 Canadian Dollar = \(\frac{1}{1.10}\) US Dollars
⇒ 1 Canadian Dollar = 0.91 US Dollars
Now we know that 1 US Dollar = 100 cents
∴ 0.91 US Dollars = 0.91 x 100 = 91 cents
Hence the value of 1 Canadian Dollar is 0.91 US Dollars or 91 cents.
To learn more about cents click here:
https://brainly.com/question/20145274
#SPJ4
Dilation is a transformation that requires a center of dilation and a scale factor.
True
False
Answers
Answer:
false
Step-by-step explanation:
In triangle abc, which side is the longest if these are the measures of the angles? m∠a = 60°, m∠b = (3x − 2)°, m∠c = (2x 7)° side is the longest side.
Answers
In triangle ABC, AC is the longest if these are the measures of the angles.
Define angles.When two lines meet at a point, an angle is created. An "angle" is the measurement of the "opening" between these two rays. It is symbolized by the character. The circularity or rotation of an angle is often measured in degrees and radians. Angles are a common occurrence in daily life. Angles are used by engineers and architects to create highways, structures, and sports venues. When two rays are linked at their ends, they create an angle in geometry. The sides or arms of the angle are what are known as these rays.
Given
Angles
m∠a = 60°, m∠b = (3x − 2)°, m∠c = (2x 7)°
Let's first solve for x and then determine m∠B and m∠C.
Since a triangle's internal angles add up to 180 degrees, we can deduce the following:
60 + 3x - 2 + 2x + 7 = 180
5x + 65 = 180
5x = 180 - 65
5x = 115
x = 23
Because of this,
m∠B = 3(23) - 2 = 67°
and m∠C = 2(23) + 7 = 53°.
Since m∠B is the biggest angle in a triangle, we know that the side opposite to B is the longest since the longest side of a triangle is always the opposite of the largest angle in the triangle. AC is on that side.
To learn more about angle, visit:
https://brainly.com/question/17221138
#SPJ4
Help asap brb.asap asap will give max points

Answers
Answer:
\(3^{3}\)
Step-by-step explanation:
Note: When you divide exponents with the same constant, the exponent will be subtracted, and vice-versa, when you multiply exponents with the same constant, the exponents will be added.
\(\frac{3^{-9} }{3^{-12} } \\= 3^{-9-(-12)} \\=3^{-9+12} \\=3^{3}\)
when dividing exponents, you subtract the exponents from each other in this case it would be 9- (-12) which would equal 3
Solve for x
■ 5(x+4)+5(2-x)
THANKS!!! :)
Answers
Answer:
30
Step-by-step explanation:
5(x+4) + 5(2-x)
5x + 20 + 10 - 5x
20 + 10
30
Answer:
30
Step-by-step explanation:
\(=5(x+4)+5(2-x)\\\\=5x+20+10-5x\\\\=5x-5x+20+10\\\\=30\)
A six sided dice is rolled twice.
What is the probability that the first roll is an even number and the second roll is a number greater than 4?
Answers
Answer: 1/6 chance
Step-by-step explanation:
FIRST ROLL:
even numbers are 2, 4, and 6
3/6 or 1/2 chance of rolling even (50%)
SECOND ROLL:
numbers greater than 4 are 5 and 6
2/6 or 1/3 chance of rolling a number greater than 4 (33 1/3%)
MATH:
1/3*1/2 = 1/6 or about 16-17%
The lowest temperature on Mars can reach –140°C while the highest temperature can be 20°C. What is the difference between the highest and lowest temperatures on Mars?
Answers
A cylindrical wire with radius a=200μm carries a current density J=2×10
8
A/m
2
. Given that the current density is uniform, find the current that flows in the region where R>2a/3
Answers
The current flowing in the region where R > 2a/3 of the cylindrical wire with radius a = 200μm and uniform current density J = 2×10^8 A/m^2 is 2.67 A.
To calculate the current in the specified region, we first need to determine the length of that region. Let's consider the length of the wire as L. The length of the region where R > 2a/3 can be calculated as L' = L - 2π(2a/3), which simplifies to L' = L - (4πa/3).
Next, we can calculate the total current flowing through the wire using the current density formula: I = J × A, where I is the current, J is the current density, and A is the cross-sectional area of the wire. The cross-sectional area A is given by A = πa^2.
Since the current density is uniform, the total current I flowing through the wire is equal to J multiplied by the cross-sectional area A. Therefore, I = J × A = J × (πa^2).
Now, we can determine the current in the region where R > 2a/3 by multiplying the total current I by the ratio of the length of that region L' to the total length L. Therefore, the current in the specified region is given by I' = I × (L'/L).
Substituting the known values into the equations, we have:
I' = (2×10^8 A/m^2) × (π(200μm)^2) × [(L - (4π(200μm)/3)) / L]
I' = 2.67 A
Therefore, the current flowing in the region where R > 2a/3 is 2.67 A.
To know more about current density, refer here:
https://brainly.com/question/29095933#
#SPJ11
A manager of a deli gathers data about the number of sandwiches sold based on the number of customers who visited the deli over several days. The
table shows the data the manager collects, which can be approximated by a linear function.
Customers
104
70
111
74
170
114
199
133
163
109
131
90
Sandwiches
If, on one day, 178 customers visit the deli, about how many sandwiches should the deli manager anticipate selling?
Answers
To estimate the number of sandwiches the deli manager should anticipate selling when 178 customers visit the deli, we can analyze the given data and approximate it using a linear function.
By observing the table, we notice that the number of sandwiches sold varies with the number of customers. This indicates a relationship between the two variables.
To estimate the number of sandwiches, we can fit a line to the data points and use the linear function to make predictions. Using a statistical software or a spreadsheet, we can perform linear regression analysis to find the equation of the best-fit line. However, since we are limited to text-based interaction, I will provide a general approach.
Let's assume the number of customers is the independent variable (x) and the number of sandwiches is the dependent variable (y). Using the given data points, we can calculate the equation of the line.
After calculating the linear equation, we can substitute the value of 178 for the number of customers (x) into the equation to estimate the number of sandwiches (y).
Please provide the data points for the number of sandwiches sold corresponding to each number of customers so that I can perform the linear regression analysis and provide a more accurate estimate for you.
Learn more about selling here
https://brainly.com/question/29136043
#SPJ11
se the ratio test to determine whether the series is convergent or divergent. [infinity] nn=1 8nIndentifyan
Answers
L = 1, the ratio test is inconclusive, and we cannot determine whether the series converges or diverges
The ratio test is a tool used to determine the convergence of an infinite series. Given a series Σ(an) from n=1 to infinity, the ratio test states that if the limit as n approaches infinity of |a(n+1)/an| equals L, then:
- If L < 1, the series converges
- If L > 1, the series diverges
- If L = 1, the test is inconclusive
Now let's apply the ratio test to the given series Σ(8n) from n=1 to infinity. To do this, we need to find the limit as n approaches infinity of |a(n+1)/an|:
|a(n+1)/an| = |8(n+1)/8n|
Simplifying the expression, we get:
|1 + 1/n|
As n approaches infinity, 1/n approaches 0, so the limit of the expression is:
|1 + 0| = 1
Since L = 1, the ratio test is inconclusive, and we cannot determine whether the series converges or diverges based solely on this test.
To know more about Ratio test.
https://brainly.com/question/30396381
#SPJ11
Questions 7 and 8 please. Really need help thank you!!

Answers
Answer:
7) sin 60° = 25√3/Z
0.8660 = 25√3/Z
Z = 50
8) using the Pythagorean theorem:
50² = (25√3)² + y²
2500 = 1875 + y²
y² = 625
y = 25
Answer:
z = 50
y = 25
Step-by-step explanation:
Using the 30, 60, 90 triangle rule
you can figure this out.
The rule says
With a 30, 60, 90 triangle
Given the shorter leg, (side across the 30 degree angle,
To find longer leg (side across the 60 degree angle):
Multiple shorter leg by radical 3.
To find hypotenuse (side across the 90 degree angle):
Multiple shorter leg by 2.
Thus
Shorter leg (side opposite 30 degree): 25
Longer leg (side opposite 60 degree):
25 radical 3
Hypotenuse(side opposite 90 degree): 50