The number of subsets that can be created from the set {1, 2, 3} is:

Answer:

2804

Step-by-step explanation:

2504 + 140 + 160 = 2804   (hint: add the 140 + 160 first. It sums up to 300 which is easy to add to 2504)

Answer:

1/42 = 0.0238

Step-by-step explanation:

We solve it using combination. for the first part the student can answer 5 questions out of 10 questions given

= 10!/5!(10-5)!

= 252

for the second part the instructor choses 5 questions out 10 for the student to solve.

= 6!/5!(6-5)!

= 6

thus the probability that the student can solve all the problems in the exam is

6/252 = 0.0238

Answer:

150 labels/ minute

Step-by-step explanation:

As you can see on the graph there is a point on (1,1 1/2)=150/1

Also 150*2=300 so it all makes sence

The value of the line integral is:

\((1/27) (49^{(3/2)} - 13^{(3/2)})\)

≈ 36.724

To evaluate the line integral:

\(\int C x^2/y^{(4/3)} ds\)

C is the curve given by x = t² and y = t^3, and ds is the element of arc length along the curve.

We can parameterize the curve as:

r(t) = (t², t³), 1 ≤ t ≤ ∛2

Then the tangent vector to the curve is:

r'(t) = (2t, 3t²)

The length of the tangent vector is:

|r'(t)| = √(4t² + 9t⁴ = t√(4 + 9t²)

So, the element of arc length ds is:

ds = |r'(t)| dt = t√(4 + 9t²) dt

The integral becomes:

\(\int C x^2/y^{(4/3)} ds\)

=\(\int(1 to 3\sqrt 2) (t^4)/(t^{(8/3)}) (t\sqrt{(4 + 9t^2)}) dt\)

= \(\int (1 to 3\sqrt 2) t^{(2/3)}\sqrt (4 + 9t^2) dt\)

To evaluate this integral, we can make the substitution u = 4 + 9t²:

u = 4 + 9t²

du/dt = 18t

dt = du/(18t)

The limits of integration become:

u(1) = 13

u(∛2) = 49

The integral becomes:

\(\int C x^2/y^{(4/3)} ds\)

= \((1/18) \int (13 to 49) u^{(1/2)} du\)

=\((1/27) (49^{(3/2)} - 13^{(3/2)})\)

So, the value of the line integral is:

\((1/27) (49^{(3/2)} - 13^{(3/2)})\)

≈ 36.724

For similar questions on line integral

https://brainly.com/question/28381095

#SPJ11

Answer:

[B] 1/25

Step-by-step explanation:

From the given:

There are letter tiles in a bag. Four A’s, five B’s, six C’s and five D’s. You select one tile, replace it, and then draw another.

To Find:

P( A and A)=______

Solution:

Since it given that:

Four A’s, five B’s, six C’s and five D’s.

Thus we have:

A,A,A,A,B,B,B,B,B,C,C,C,C,C,C,D,D,D,D,D

Total number of letters tiles = 20

Probability of selecting A = 4/20  = 1/5

Probability of selecting A  = 4/20 = 1/5

P( A and A)= 1/5 × 1/5 = 1/25

Thus, the answer is [B] 1/25

Kavinsky

Answer:1.) 1.56

             2.)0.52

Step-by-step explanation:

Answer:

That person's answer is right. 1.56      0.52

Step-by-step explanation:

We may type the following expression into a calculator to calculate 13822 x 623/14: 13822 * 623/14 = 615079. 6 x 105 is equal to 1.4 x 104 x 4.4 x 101. Our response to part a) makes sense because 615079 is not far from 6 x 105.

We may type the following expression into a calculator to calculate 13822 x 623/14: 13822 * 623/14 = 615079

As a result, 615079 is the precise value of 13822 x 623/14.

Using approximations to 1 significant figure, we may determine whether the response makes logical.

The difference between 13822 and 623/14 is around 1.4 x 104 and 4.4 x 101, respectively.

Hence, 6 x 105 is equal to 1.4 x 104 x 4.4 x 101.

Our response to part a) makes sense because 615079 is not far from 6 x 105.

learn more about calculator here:

https://brainly.com/question/30151794

#SPJ4

Answer:

20

Step-by-step explanation:

5(x-1)

Replace x with its value.

5(5-1)

Solve parenthesis first.

5(4)

Multiply.( multiply 5 times 4)

20

Answer:

Domain is Set of all real numbers

Step-by-step explanation:

1. Domain : It is the set of values for which our function is defined and it gives some value of f(x) for every value of x in it.

Answer:

2x+5+[6/(x+4)]

r(x)=6 and q(x)= 2x+5

Step-by-step explanation:

(2x^2)+13x +26)/(x+4) =

2x+5+[6/(x+4)]

r(x)=6 and q(x)= 2x+5

using polynomial calculator

Answer:

A

Step-by-step explanation:

First, we can FOIL the term "\(-10(x-7)\)":

\(-10x+70\)

Back into the original equation:

\(-10x+70-3x\)

Combine like terms:

\(-13x+70\)

Hope this helps!

Answer:

A. -13x + 70

I had this question before.

Answer:

15%

Step-by-step explanation:

2+x=3.5

x=3.5-2

x=1.5

1.5 is the amount of miles gained,lets convert to a fraction

1.5/10 × 100/1

= 15%

Answer:

Step-by-step explanation:

This indicates that a student's projected test score would be 100 if they did not view any videos while studying (x = 0).

The linear equation is given as,

y = mx + c

Where m is the slope of the line and c is the y-intercept of the line.

The slope is the ratio of rise over run.

This indicates that a student's projected test score would be 100 if they did not view any videos while studying (x=0). However, the anticipated exam score declines by 2 points for each extra hour that kids watch videos as the number of hours they watch rises.

More about the linear equation link is given below.

https://brainly.com/question/11897796

#SPJ1

Answer:

please be more specific

Step-by-step explanation:

a) To derive the integrated rate law from the second order rate law, we start with the differential rate equation:

\[ \frac{d[A]}{dt} = -k[A]^2 \]

where \([A]\) represents the concentration of the reactant A and \(k\) is the rate constant.

To integrate this equation, we separate the variables and integrate both sides:

\[ \int \frac{d[A]}{[A]^2} = -\int k dt \]

This gives us:

\[ -\frac{1}{[A]} = -kt + C \]

where \(C\) is the integration constant. We can rearrange this equation to isolate \([A]\):

\[ [A] = \frac{1}{kt + C} \]

To determine the value of the integration constant \(C\), we use the initial condition \([A] = [A]_0\) at \(t = 0\). Substituting these values into the equation, we get:

\[ [A]_0 = \frac{1}{C} \]

Solving for \(C\), we find:

\[ C = \frac{1}{[A]_0} \]

Substituting this value back into the equation, we obtain the integrated rate law:

\[ [A] = \frac{1}{kt + \frac{1}{[A]_0}} \]

b) The integrated rate law describes the relationship between the concentration of a reactant and time in a chemical reaction. It provides a mathematical expression that allows us to determine the concentration of the reactant at any given time, given the initial concentration and rate constant.

In the derived integrated rate law, we observe that the concentration of the reactant \([A]\) decreases with time (\(t\)). As time progresses, the denominator \(kt + \frac{1}{[A]_0}\) increases, leading to a decrease in the concentration. This is consistent with the second order rate law, where the rate of the reaction is directly proportional to the square of the reactant concentration.

The integrated rate law also highlights the inverse relationship between the concentration of the reactant and time. As the denominator increases, the concentration decreases. This relationship is important in understanding the kinetics of a chemical reaction and can be used to determine reaction orders and rate constants through experimental data analysis.

By deriving the integrated rate law, we can gain insights into the behavior of chemical reactions and make predictions about the concentration of reactants at different time points. This information is valuable in various fields, including chemical engineering, pharmaceuticals, and environmental science, as it allows for the optimization and control of chemical processes.

To know more about rate, refer here:

https://brainly.com/question/25565101

#SPJ11

Answer:

If I did my math right it should be 10.20

Step-by-step explanation:

-78.55 + 128.75 = 50.2

50.2 - 40 = 10.2

And then obviously just add the zero at the end bc its money

We have the following polynomial:

Now, we can rewrite the polynomial in descending order as follows:

As we can see, the order in descending order takes into account the values for the exponents of the variable (an unknown value), x. Since the degree of a polynomial is the highest degree of any term of the polynomial, and this term is represented by:

In other words, the degree of a polynomial is the highest power we have for any term in the polynomial.

Therefore, the degree of the polynomial is 5, and we can write it, in descending order as follows:

In summary, therefore, the degree of the polynomial is 5, in this case, and if we write it in descending order, we have:

The future value of $100 compounded continuously at an annual rate of 6% for 12 years is $205.31.

The formula for calculating the future value of a continuously compounded investment is:

A = Pe^(rt)

Where:

A = the future value of the investment

P = the principal amount (initial investment)

e = Euler's number (approximately 2.71828)

r = the annual interest rate (as a decimal)

t = the time period (in years)

Using this formula, we can calculate the future value of $100 compounded continuously at an annual rate of 6% for 12 years as follows:

A = 100 x e^(0.06 x 12)

A = 100 x e^0.72

A = 100 x 2.0531

A = $205.31

Therefore, the value obtained is $205.31.

To know more about annual rate refer here:

https://brainly.com/question/29766128#

#SPJ11

Answer:

300

Step-by-step explanation:

im smart

To find the volume of the composite figure, we first need to break it down into simpler shapes. We can see that the composite figure is made up of a rectangular prism and a triangular prism.

The rectangular prism has a length of 6 cm, a width of 4 cm, and a height of 7 cm. Therefore, its volume is:

Volume of rectangular prism = length x width x height = 6 cm x 4 cm x 7 cm = 168 cubic cm

The triangular prism has a base of 3 cm, a height of 8 cm, and a length of 10 cm. Therefore, its volume is:

Volume of triangular prism = (1/2) x base x height x length = (1/2) x 3 cm x 8 cm x 10 cm = 120 cubic cm

To find the volume of the composite figure, we add the volumes of the rectangular prism and the triangular prism:

Volume of composite figure = Volume of rectangular prism + Volume of triangular prism = 168 cubic cm + 120 cubic cm = 288 cubic cm

Therefore, the volume of the composite figure is 288 cubic centimeters.

To learn more about composite figure, click here:

brainly.com/question/27234680

#SPJ11

B is the assertion that captures the final behavior of the function f(x) = 3|x 7| 7. As x moves closer to zero, f(x) moves closer to positive infinity.

An equation is a mathematical formula that expresses equality by joining two expressions together with the equal symbol =. The definition of an equation in algebra is a mathematical statement proving the equality of two mathematical expressions. In the equation 3x + 5 = 14, for instance, the terms 3x + 5 and 14 are separated by an equal sign. An equal sign is a part of all mathematical formulas, including equations. Often, algebra is used in equations. In mathematics, algebra is employed when we don't know the precise quantity to calculate

From the question,

\(f(x) = 3|x − 7| − 7\\when x = -101\\then, f(x) = 3|-101 − 7| − 7\\f(x) = 3|-108| − 7\\\)

f(x) = 3 × 108 − 7

f(x) = 324 -7

\(f(x) = 317\\Also, when x = -3000\\then, f(x) = 3|-3000- 7| - 7\\f(x) = 3|-3007| - 7\\f(x) = 3 × 3007 - 7\\\)

f(x) = 9021 - 7

f(x) = 9014

To know more about equation visit:

brainly.com/question/649785

#SPJ4

Answer:

a = 1;

b = -7;

c = -4

Step-by-step explanation:

\( {x}^{2} - 7x = 4\)

Write it in the following form:

\(a {x}^{2} + bx + c = 0\)

Move 4 to the other side (make sure to change its sign to a negative)

\(1 {x}^{2} - 7x - 4 = 0\)

a = 1;

b = -7;

c = -4

The option a. 2/13 is the correct answer.

Given:In a clinic, when 130 patients examined90 had heart trouble50 had diabetes30 had both diseases

We have to find the probability that the patient did not have heart trouble or diabetes using the formula of conditional probability:P(A or B) = P(A) + P(B) - P(A and B)

The probability of a patient not having heart trouble or diabetes is given by:

Probability (not have heart trouble or diabetes) = P(neither heart trouble nor diabetes) = P(only neither)

The number of patients having only neither heart trouble nor diabetes can be found by subtracting the patients having heart trouble,

the patients having diabetes, and the patients having both diseases from the total number of patients.

Hence, the number of patients having only neither heart trouble nor diabetes is:(130 - 90 - 50 + 30) = 20

Probability (not have heart trouble or diabetes) = P(only neither) = 20/130 = 2/13

Therefore, the option a. 2/13 is the correct answer.

To know more about Probability,visit:

https://brainly.com/question/31828911

#SPJ11

The probability that the patient did not have heart trouble or diabetes is 2/13.

The correct option is a) 2/13.

Step 1: Find the probability of having both heart trouble and diabetes:

P(Heart trouble and Diabetes) = Number of patients with both conditions / Total number of patients

                           = 30 / 130

                           = 3/13

Step 2: Find the probability of having only heart trouble:

P(Only Heart trouble) = Number of patients with heart trouble - Number of patients with both conditions / Total number of patients

                     = (90 - 30) / 130

                     = 60/130

                     = 6/13

Step 3: Find the probability of having only diabetes:

P(Only Diabetes) = Number of patients with diabetes - Number of patients with both conditions / Total number of patients

                = (50 - 30) / 130

                = 20/130

                = 2/13

Step 4: Find the probability of not having heart trouble or diabetes:

P(Not Heart trouble or Diabetes) = 1 - P(Only Heart trouble) - P(Only Diabetes) - P(Heart trouble and Diabetes)

                              = 1 - (6/13) - (2/13) - (3/13)

                              = 1 - 11/13

                              = 2/13

Therefore, the probability that the patient did not have heart trouble or diabetes is 2/13.

The correct option is a) 2/13.

To know more about probability, visit:

https://brainly.com/question/31828911

#SPJ11

Answer:

The numbers are 16 and 44.

Step-by-step explanation:

Leg x be the first number, then the other number is 3x - 4.

So x + 3x - 4 = 60

4x = 60 + 4 = 64

x = 64/4

x = 16.

The other number is 3(16) - 4 = 44.

Step-by-step explanation:

Hey there!

Given;

The sum is numbers 60.

Let one number be x then, the next number is 3x-4.

Now, according to the question,

x+3x-4 = 60

4x = 60+4

\(x = \frac{64}{4} \)

x = 16.

And another number is 3×16-4.

= 44.

Hope it helps...

(a) The confidence level for the procedure "Sample proportion ± 1.645 ✕ standard error" is approximately 90%.

(b) The confidence level for the procedure "Sample proportion ± 2 ✕ standard error" is approximately 95%.

(c) The confidence level for the procedure "Sample proportion ± 2.33 ✕ standard error" is approximately 99%.

(d) The confidence level for the procedure "Sample proportion ± 2.58 ✕ standard error" is approximately 99.5%.

Confidence level refers to the level of confidence or certainty that can be associated with a particular statistical estimation or inference procedure. It is commonly used in statistical analysis to express the amount of confidence one can have in the accuracy or reliability of a statistical estimate or result.

In the context of confidence intervals, which are used to estimate unknown population parameters based on sample data, the confidence level represents the probability or percentage of times that the calculated confidence interval would contain the true population parameter, if the same estimation procedure were repeated multiple times with different samples.

Learn more about confidence level here: https://brainly.com/question/15712887

#SPJ1

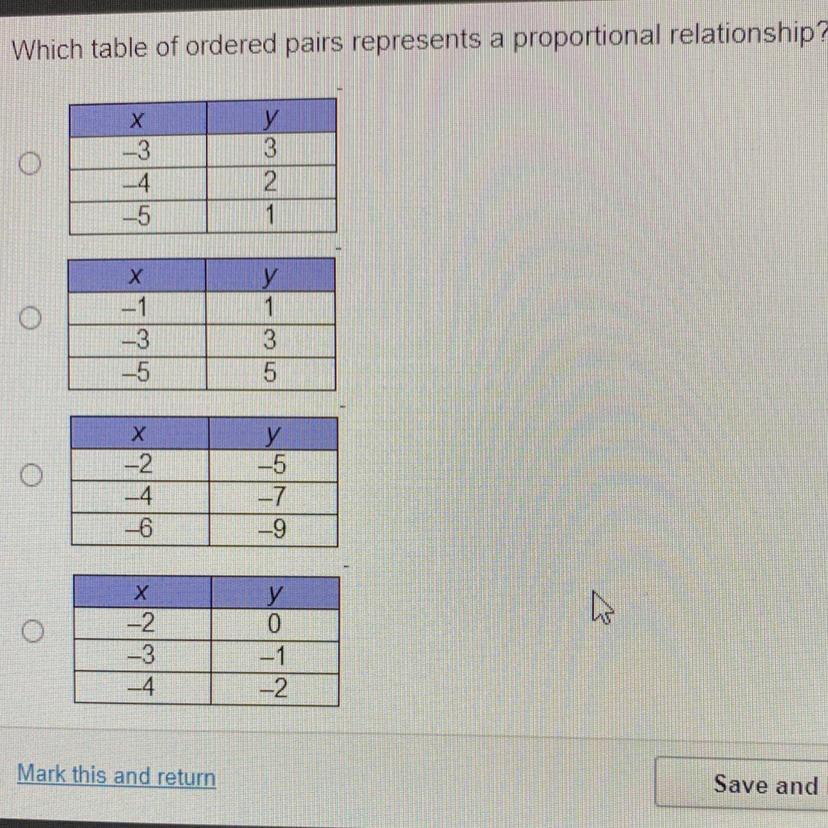
Answer:

second x -1,-3,-5 y 1 3 5 for proportional relation

a. there are 524,288 frames in the system. b. the maximum number of frames is determined by the number of bits required to represent the page number, and the number of pages that can be addressed is limited by the size of the logical address space. c. 3 bits are needed to represent the page number 8, and 12 bits are needed to represent the offset 12.

a) The system has 524,288 frames. This can be calculated by dividing the maximum size of the logical address space (1MB) by the size of each frame (4KB).

1MB = 2^20 bytes

4KB = 2^12 bytes

Number of frames = (1MB / 4KB) = (2^20 / 2^12) = 2^(20-12) = 2^8 = 256

Therefore, there are 524,288 frames in the system.

b) The maximum number of frames that can be allocated to a process in this system is 256. This is because the maximum number of frames is determined by the number of bits required to represent the page number, and the number of pages that can be addressed is limited by the size of the logical address space.

c) i. The page number 8 can be represented using 3 bits. This is because there are 2^3 = 8 possible page numbers (0 to 7).

ii. The offset 12 can be represented using 12 bits. This is because there are 2^12 = 4,096 possible offsets (0 to 4,095).

Therefore, 3 bits are needed to represent the page number 8, and 12 bits are needed to represent the offset 12.

Learn more about frames here

https://brainly.com/question/29649442

#SPJ11

Answer: 5

Step-by-step explanation:

The perimeter of the nonagon attached is

124.5

The formula for the perimeter of a nonagon (a polygon with nine sides):

Perimeter = 9 * side length

side length = 2 * apothem * tan(π/9)

= 2 * 19 * tan(π/9)

= 13.831

The perimeter

Perimeter = 9 * side length

Perimeter = 9 * 13.81

Perimeter = 124.5

Learn more about perimeter at

https://brainly.com/question/397857

#SPJ1

There are a couple ways to solve this but I will show you the way I think is easiest:

You should make the fraction parts of the numbers have an equivalent denominator. Right now, the denominators are 10 and 5. It would be best to make both denominators equal 10.

In - 2 \(\frac{3}{5}\),  3/5 x 2 = 6/10

So now the fractions are \(-10\frac{7}{10} - 2\)\(\frac{6}{10}\)

Remember the sign rules!

The answer is - 13\(\frac{3}{10}\)

I hope this helps!

Answer:

     \(-\frac{133}{10}\)

Step-by-step explanation:

\(-10\frac{7}{10}\) = \(-\frac{107}{10}\)               (10x(-10)+7)

\(-2\frac{3}{5}\) = \(-\frac{13}{5}\)                   (5x(-2)+3)

lcm of 10 and 5 is 10:

\(-\frac{107}{10} -\frac{13}{5}\)

\(\frac{-107-26}{10}\)

\(-\frac{133}{10}\)

Please mark as brainliest :)))))))))))))