the notation limx→2f(x)=5 states that the limit of the function f at x=5 is 2.

Answer: 4 over 5 is not a whole number and so it cannot be expressed as a whole number.

Step-by-step explanation:

Answer:

50%

Step-by-step explanation:

There are a total of 20 marbles.

10/20 equal 50%

Answer:

50%

Step-by-step explanation:

Answer:

ABCD forms a rhombus

Step-by-step explanation:

When you graph it out on a graph, the points make a rhombus

5777 divided by 160 is 36.10625.

the data is given in the the question is as follows:

5777 divided by 16 , that means,  5777 / 160 = 36.10625

                  36.10625

          160| 5777

                 -  5760

                          170

                      -   160

                             1000

                           - 960

                                 400

                             -    320

                                      800

                                   -   800

                                        000

Division is just opposite of the multiplication . There are four basic operations in mathematics and division is from one the basic operations . the four operation are addition, subtraction , multiplication , division.  Division is used when we split the large groups into the smaller one , so that each group will have equal items. there are different types of method used for division. the above one is the chunking method or in simple word repeated subtraction method.

Thus, 5777 divided by 160 is 36.10625.

To learn more about division here

https://brainly.com/question/21416852

#SPJ1

The number of students who took the test on Monday is found to be 15, hence the correct option is B.

Let us assume that the number of student taking test on Monday is n. The total score for Monday's test is n times the average score of 80.4,

Monday's total score = 80.4n

When the student who missed the test on Monday took the test on Tuesday and scored 90, the total score became,

Total score = 80.4n + 90

The new average score of 81 can be expressed as,

81 = Total score / (n+1)

Substituting the value of the total score, we get,

81 = (80.4n + 90)/(n+1)

Multiplying both sides by n+1, we get,

81(n+1) = 80.4n + 90

Expanding the brackets,

81n + 81 = 80.4n + 90

Simplifying,

0.6n = 9

n = 15, so, the number of students who took the test on Monday is 15.

To know more about arithmetic mean, visit,

https://brainly.com/question/1136789

#SPJ4

-17/2

Step-by-step explanation:

30-8(8)+4y

30=64+4y

30-64=4y

-34=4y

y= -34/4

y= -17/2

hope it helps!

If there are 30 students in the class, then the number of students who play soccer but do not play basket-ball are 13 students.

The total-students in the class is = 30 students,

The Number of students who play basketball is = (2/5) × 30 = 12,

The Number of students who play soccer is = (7/10) × 30 = 21,

⇒ Number of basketball players who also play soccer = (2/3) × 12 = 8,

So, out of the 21 students who play soccer, 8 also play basketball.

To find the number of students who play soccer but not basketball, we can subtract the number of students who play both from the total number of soccer players:

⇒ 21 - 8 = 13 students play soccer but not basketball.

Therefore, the required number of students are 13 students.

Learn more about Students here

https://brainly.com/question/9552804

#SPJ4

The volume of the prism is determined as  1,416 m³ and the surface area of the prism is 664.8 m².

The volume of the prism is determined from the product of base area and slant height of the prism.

Base of the prism, A = ¹/₂bh = ¹/₂ x 12 x 20 = 120 m²

Volume = AL

where;

L² = (12/2)² + (20.3/2)²

L² = 6² + 10.15²

L² = 139.0225

L = 11.8 m

V = AL

V = 120 x 11.8 = 1,416 m³

A = bh + pL

A = (12 x 20) + 11.8(12 + 12 + 12)

A = 664.8 m²

Learn more about volume of prism here: https://brainly.com/question/23963432

#SPJ1

Answer:

= 2

Step-by-step explanation:

Answer:

Look into this site called MathPapa It will do almost any problem you want (as long as It is like 10+28 or 7(6)*6(7) something like that but It is a really good calculator check It out! See screen shot

Step-by-step explanation:

Please do tell If I am incorrect :)

In the given figure, the measure of angle ABD is 120 degrees

From the given figure

The measure of angle CBD = 60 degrees

We know the sum of angles on a straight line add up to 180 degrees.

Here the line AC is straight line

Therefore, the sum of the measure of angle ABD and measure of angle CBD is equal to 180 degrees, so the angle ABD and angle CBD are supplementary angles

Angle ABD + Angle CBD = 180 degree

Substitute the values in the equation

∠ABD + 60 = 180

∠ABD = 180 - 60

∠ABD = 120 degree

Therefore, the angle ABD is 120 degrees

Learn more about supplementary angle here

brainly.com/question/13045673

#SPJ4

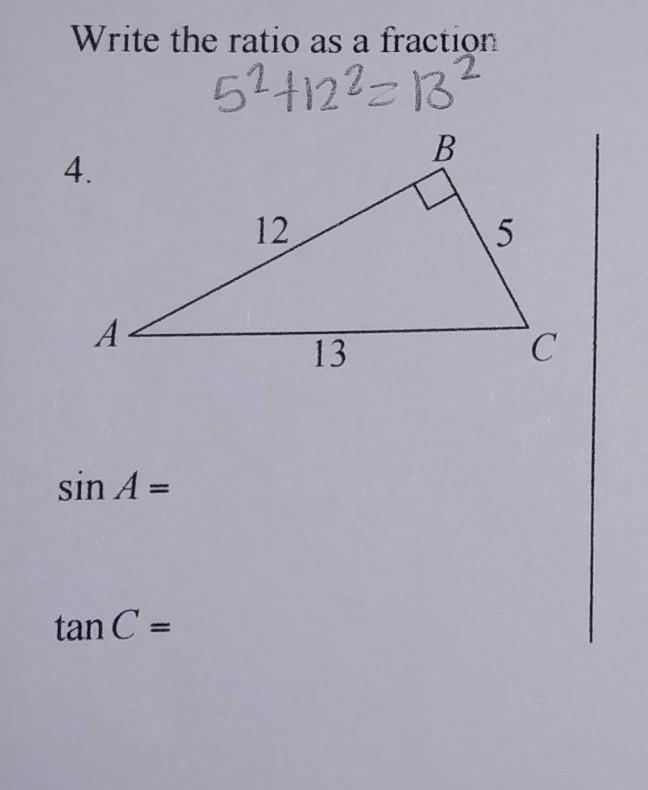
Answer:

Sin A = 5/13; tan C = 12/5

Step-by-step explanation:

Sin = opposite / hypotenuse. The opposite of A is 5, and the hypotenuse is 13, therefore Sin A = 5/13.

Tan = opposite / adjacent. The opposite of C is 12, and the adjacent is 5, so tan C = 12 / 5

The remainder when dividing 4x⁴ - 8x³ - x + 10 by x² - 4 is -33x + 74.

To find the remainder when the polynomial 4x⁴ - 8x³ - x + 10 is divided by x² - 4, we can use polynomial long division.

             4x² - 8x + 16

         ___________________

x² - 4 |  4x⁴- 8x³ - x + 10

         - (4x⁴ - 16x²)

         ______________

                - 8x³ + 16x² - x + 10

                -(- 8x³ + 32x)

                ______________

                          16x² - 33x + 10

                        - (16x² - 64 )

                          ______________

                                    -33x + 74

Therefore, the remainder when dividing 4x⁴ - 8x³ - x + 10 by x² - 4 is -33x + 74.

Learn more about polynomial long division method here

https://brainly.com/question/30989082

#SPJ4

Answer:

1. 8.04

2. 20 feet

3. d

4. c

5. Ed = 4

Step-by-step explanation:

Pythagoras theorem

a² + b² = c²

4² + b² = 6²

16 + b² = 36

b² = 20

square root 20 = 4.47

6 ÷ 4.47 = 1.34

6 × 1.34 = 8.04

Answer:

Magnitude is 5

Step-by-step explanation:

Using the formula for calculating the distance between two points expressed as:

D = √(x2-x1)²+(y2-y1)²

Given the coordinates  (3,5) and (-1,2)

D = √(2-5)²+(-1-3)²

D = √(-3)²+(-4)²

D = √9+16

D = √25

D = 5

Hence the magnitude is 5

Answer:

<1 and <3

<1 and <4

<2 and <1

<2 and <3

Step-by-step explanation:

Find the diagram attached

First know that supplementary angles are angles that sums up to 180degrees. Since the sum of angles on a straight line is also 180degrees, then the pair of supplementary angles must lie on the same straight line.

According to the given diagram, the following angles are supplementary since they lie on the same straight line;

<1 and <3

<1 and <4

<2 and <1

<2 and <3

The sum of all the pair of angles is 180 degrees

b c d e

Step-by-step explanation:

Answer:

v=20π ft/s

Step-by-step explanation:

Given:

Distance from the security car to the movie theater, D=25 ft

Distance of the reflection from the car, d=30 ft

Speed of rotation of the strobe lights, 2 rev/s

To find the speed at which the reflection of the security strobe lights is moving along the wall of the movie theater, we need to calculate the linear velocity of the reflection when it is 30 ft from the car.

We can start by finding the angular velocity in radians per second. Since the strobe lights rotate at 2 revolutions per second, we can convert this to radians per second.

ω=2πf

=> ω=2π(2)

=> ω=4π rad/s

The distance between the security car and the reflection on the wall of the theater is...

r=30-25= 5 ft

The speed of reflection is given as (this is the linear velocity)...

v=ωr

Plug our know values into the equation.

v=ωr

=> v=(4π)(5)

∴ v=20π ft/s

Thus, the problem is solved.

The speed of the reflection of the security strobe lights along the wall of the movie theater is 2π ft/s.

To solve this problem, we can use the concept of related rates. Let's consider the following variables:

x: Distance between the security car and the movie theater wall

y: Distance between the reflection of the security strobe lights and the security car

θ: Angle between the line connecting the security car and the movie theater wall and the line connecting the security car and the reflection of the strobe lights

We are given:

x = 25 ft (constant)

y = 30 ft (changing)

θ = 2 revolutions per second (constant)

We need to find the speed at which the reflection of the security strobe lights is moving along the wall (dy/dt) when the reflection is 30 ft from the car.

Since we have a right triangle formed by the security car, the movie theater wall, and the reflection of the strobe lights, we can use the Pythagorean theorem:

x^2 + y^2 = z^2

Differentiating both sides of the equation with respect to time (t), we get:

2x(dx/dt) + 2y(dy/dt) = 2z(dz/dt)

Since x is constant, dx/dt = 0. Also, dz/dt is the rate at which the angle θ is changing, which is given as 2 revolutions per second.

Plugging in the known values, we have:

2(25)(0) + 2(30)(dy/dt) = 2(30)(2π)

Simplifying the equation, we find:

60(dy/dt) = 120π

Dividing both sides by 60, we get:

dy/dt = 2π ft/s

For more such question on speed. visit :

https://brainly.com/question/26046491

#SPJ8

The probability of buying coffee is 77%, the probability of buying a bagel is 36%, and the probability of buying both coffee and a bagel is 22%. Therefore, if one customer is selected at random, there is a 77% chance they will buy coffee, a 36% chance they will buy a bagel, and a 22% chance they will buy both coffee and a bagel.

The probability of buying coffee is 77%. This can be calculated as 77/100, which is equivalent to 0.77.

The probability of buying a bagel is 36%. This can be calculated as 36/100, which is equivalent to 0.36.

The probability of buying both coffee and a bagel is 22%. This can be calculated as 22/100, which is equivalent to 0.22.

At a Dunkin' Donuts drive-thru, the probability of buying coffee is 77%, the probability of buying a bagel is 36%, and the probability of buying both coffee and a bagel is 22%. This means that if one customer is selected at random, there is a 77% chance they will buy coffee, a 36% chance they will buy a bagel, and a 22% chance they will buy both coffee and a bagel. To calculate these probabilities, we divide the respective percentages (77%, 36%, and 22%) by 100. The result of this calculation is 0.77 for the probability of buying coffee, 0.36 for the probability of buying a bagel, and 0.22 for the probability of buying both coffee and a bagel. This means that if one customer is selected at random, there is a 77% chance they will buy coffee, a 36% chance they will buy a bagel, and a 22% chance they will buy both coffee and a bagel.

Learn more about probability here

https://brainly.com/question/11234923

#SPJ4

Answer:

16

Step-by-step explanation:

4x16=64

being perimeter

Answer:

The mean fibre diameter of angora down fibres is around 12 to 14 m and the fibre length is up to 60 mm. The density of the fibre is 1.14 g/cm3, and hence lighter than wool (density: 1.33 g/cm3). The Angora rabbit hair is considered to be the easiest fibre to identify under microscope than other specialty fibres.

CHOOSE ME BRAINLIEST

An experiment usually has three kinds of variables: independent, dependent, and controlled. The independent variable is the one that is changed by the scientist.

In mathematical modeling, statistical modeling, and experimental sciences, there are dependent and independent variables. Dependent variables get their name because, during an experiment, their values are investigated under the presumption or requirement that they are dependent on the values of other variables due to some law or rule.

The variable you alter, regulate, or change in an experimental study to examine its effects is known as an independent variable. It is named "independent" because it is unaffected by any other study variables.

Learn more about independent variable here

https://brainly.com/question/25223322

#SPJ4

Option A is the correct answer.

For an experiment involving 2 Levels of factor A and 3 levels of factor B with a sample of n = 5 in each treatment condition, we need to calculate the value for df within treatments.

The formula to calculate df within treatments is given by, df within treatments = (A - 1) (B - 1) (n - 1)Where, A = Levels of factor AB = Levels of factor Bn = Sample size= 2 levels of factor A= 3 levels of factor B= 5 in each treatment conditionNow, df within treatments = (A - 1) (B - 1) (n - 1)= (2 - 1) (3 - 1) (5 - 1)= 1 × 2 × 4= 8Hence, the value of df within treatments is 8.

Learn more about factor

https://brainly.com/question/14549998

#SPJ11

The equation that can be used to determine the radius of the can isr = √(v/πh)

For example, Y is the subject of the following equations. Y = x + 1, Y = 4 + 2x, Y = 2(2x – 3). In the relation v=u + at, v is said to be the subject. When a formula is rearranged so that a different letter becomes the subject, this process is referred to as changing the subject of the relation.

Similar making r the subject in V= π r^2 h

divide both sides by πh

V/πh = r²

r² = V/πh

r = √(V/πh)

therefore the radius of the can be obtained from

r = √(V/πh)

learn more about change of subject from

https://brainly.com/question/28640952

#SPJ1

Therefore, integrate the norm of the curve's tangent vector over a specified interval. An example curve could be y = x^2, with the arc length calculated by integrating the square root of 1 + (2x)^2 over a given interval.

A line integral can determine the arc length of a curve c by integrating the norm of the curve's tangent vector over a specified interval. The formula for arc length is given by the integral of the middle of the curve's derivative with respect to its parameter. This involves taking the square root of the sum of the squares of the components of the derivative and integrating this result over the interval of interest. An example of a curve that is not part of a circle could be the curve defined by the equation y = x^2. To calculate its arc length, we would first need to find its derivative, which is y' = 2x. Then, we would integrate the square root of 1 + (2x)^2 over the interval of interest, such as from x = 0 to x = 2.

Therefore, integrate the norm of the curve's tangent vector over a specified interval. An example curve could be y = x^2, with the arc length calculated by integrating the square root of 1 + (2x)^2 over a given interval.

Learn more about the confidence interval here:

https://brainly.com/question/20309162

#SPJ11

Answer:

X= 5, -2

Step-by-step explanation:

This would be the answer if you are looking to "solve"

By evaluating P(x) for each of the possible rational roots, we find that the rational roots of P(x) = 0 are: x = -2, 1/7, and 2/7. To find the rational roots of the polynomial P(x) = 7x³ - x² - 5x + 14, we can apply the rational root theorem.

According to the theorem, any rational root of the polynomial must be of the form p/q, where p is a factor of the constant term (14 in this case) and q is a factor of the leading coefficient (7 in this case).

The factors of 14 are ±1, ±2, ±7, and ±14. The factors of 7 are ±1 and ±7.

Therefore, the possible rational roots of P(x) are:

±1/1, ±2/1, ±7/1, ±14/1, ±1/7, ±2/7, ±14/7.

By applying these values to P(x) = 0 and checking which ones satisfy the equation, we can find the actual rational roots.

By evaluating P(x) for each of the possible rational roots, we find that the rational roots of P(x) = 0 are:

x = -2, 1/7, and 2/7.

These are the rational solutions to the polynomial equation P(x) = 0.

Learn more about rational roots from the given link!

https://brainly.com/question/29629482

#SPJ11

Answer:

(0,10)

Step-by-step explanation:

-x + 2y = 20

2y = x +20

y = 1/2x + 10

This is slope-intercept form. The y-intercept is 10.

(0,10)

Answer:

(0, 10)

Step-by-step explanation:

Can be simplified to

2y = x+20 by adding x to both sides

then divide by 2 to get to slope intercept form: y = ax+b

b is the y-intercept

y = 1/2x + 10

so the answer is 10

The variance of the distribution is 7/180. Hence, the mean and the variance of the distribution are 7/6 and 7/180 respectively.

Given, f(x) = 42x (1-x) on 0 ≤ x ≤ 1, the task is to determine the mean and variance of the distribution. So, first, let us calculate the mean of the distribution using the following formula:

The mean of the distribution is given by

μ = ∫x.f(x)dx

From the above formula, the mean can be calculated as

μ = ∫x.42x(1-x)dx= 42∫x²-x³dx

Since, the integration limits are 0 to 1, so the integration can be done as follows.

μ = 42[ x³/3 - x⁴/4]0 to 1= 42[1/3 - 1/4]= 14/12= 7/6

So, the mean of the distribution is 7/6.

The next step is to calculate the variance of the distribution, which can be calculated using the following formula:

The variance of the distribution is given by

σ² = ∫(x-μ)².f(x)dx

We have already calculated the value of μ as 7/6. So, substituting the value in the above formula, we get

σ² = ∫(x - 7/6)².42x(1-x)dx= 42∫(x - 7/6)².x(1-x)dx

Since, the integration limits are 0 to 1, so the integration can be done as follows.

σ² = 42[ ∫(x²-14/6x + 49/36)x(1-x)dx]0 to 1= 42[ ∫(x³-14/6x² + 49/36x)dx - ∫(x⁴-14/6x³ + 49/36x²)dx]0 to 1= 42[ 1/4 - 7/18 + 49/216 - 1/5 + 7/24 - 49/180]

On solving, we get

σ² = 7/180

Learn more about distribution

https://brainly.com/question/29664850

#SPJ11

Answer:

z = 8/5 OR 1 3/5

Step-by-step explanation:

Step 1: Simplify both sides of the equation.

Step 2: Subtract 3z from both sides.

Step 3: Add 2 to both sides.

Step 4: Divide both sides by 5.

Answer:

75% were well done

Step-by-step explanation:

6*100=600

600/8 = 75

Answer:

0+4=4

So new temperature was 4 degrees Celsius

Step-by-step explanation: