The mathematical language we use when introducing base-ten words is important to the development of the ideas. Identify the statement that consistently connects to the standard approach.
A) Sixty-nine.
B) Nine ones and 6 tens.
C) 6 tens and 9.
D) 6 tens and 9 ones.
Answers
brainliest?
Related Questions
in the diagram below chords ab and cd intersect at e if mAEC =4x mAC=120 and mDB = 2x what is the value of x
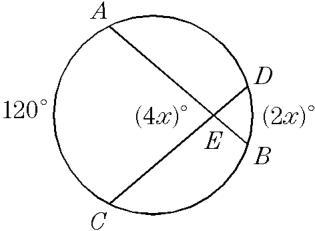
Answers
Answer:
x = 20--------------------------
According to the Angles of Intersecting Chords Theorem, the angle between two chords is half the sum of the intercepted arc measures :
m∠AEC = m∠DEB = (mAC + mDB)/2Substitute and solve for x:
4x = (120 + 2x)/24x = 60 + x3x = 60x = 20Which of the following variables is discrete? Head circumference of infants Finishing times for a 100 meter race Number of televisions in a household Volume of soda cans The least squares method minimizes the sum of which of the following? The difference between the fitted value and the true value The correlation coefficient The squared difference between the fitted value and the true value The covariance
Answers
The variable "Number of televisions in a household" is discrete among the given options. The least squares method minimizes the sum of the squared difference between the fitted value and the true value.
Discrete variable:
Among the given options, the "Number of televisions in a household" is a discrete variable. Discrete variables are those that take on a finite or countable number of distinct values. In this case, the number of televisions can only be a whole number (1, 2, 3, etc.), making it a discrete variable.
Least squares method:
The least squares method is used to fit a mathematical model to a set of data points by minimizing the sum of the squared differences between the fitted values and the true values. This means that it aims to find the line (or curve) that best represents the relationship between the variables by reducing the overall error.
Minimizing the sum of squared differences:
The least squares method minimizes the sum of the squared differences between the fitted value and the true value. By squaring the differences, it gives more weight to larger errors and effectively penalizes outliers more heavily. This approach helps to find the best-fitting line or curve that is closest to the actual data points.
In summary, the discrete variable among the given options is the "Number of televisions in a household." The least squares method minimizes the sum of the squared difference between the fitted value and the true value.
Learn more about variables here:
brainly.com/question/29045587
#SPJ11
Another famous puzzle used as an example in the study of artificial intelligence seems first to have appeared in a collection of problems, Problems for the Quickening of the Mind, which was compiled about A.D. 775. It involves a wolf, a goat, a bag of cabbage, and a ferryman. From an initial position on the left bank of a river, the ferryman is to transport the wolf, the goat, and the cabbage to the right bank. The difficulty is that the ferryman’s boat is only big enough for him to transport one object at a time, other than himself. Yet, for obvious reasons, the wolf cannot be left alone with the goat, and the goat cannot be left alone with the cabbage. How should the ferryman proceed?
Answers
The ferryman should transport the goat first, then return alone to bring the wolf, leaving the goat on the right bank. Finally, he should transport the cabbage and leave it with the wolf.
In order to solve this puzzle, the ferryman must make a series of careful moves to ensure the safety of the wolf, goat, and cabbage. The first step is to transport the goat to the right bank, leaving it there. The ferryman then returns to the left bank alone.
He takes the wolf across the river, but before leaving it on the right bank, he brings the goat back to the left bank. Now, the goat and cabbage are on the same side, while the wolf remains on the right bank.
The ferryman transports the cabbage to the right bank, leaving it there, and then returns alone to the left bank. Finally, he takes the goat across the river one last time, completing the puzzle. This sequence of moves ensures that the wolf and goat are never left alone together, nor are the goat and cabbage.
for such more questions on transport
https://brainly.com/question/21287562
#SPJ8
what is slope if -3
Answers
Answer:
yep
Step-by-step explanation:
use the kkt
Use the method of steepest ascent to approximate the solution to max z = -(x₁ - 3)² - (x₂ - 2)² s. t. (x₁, x₂) E R²
Answers
To approximate the solution and maximize the given objective function we need to find the steepest ascent direction and iteratively update the values of x₁ and x₂ to approach the maximum value of z.
The method of steepest ascent involves finding the direction that leads to the maximum increase in the objective function and updating the values of the decision variables accordingly. In this case, we aim to maximize the objective function z = -(x₁ - 3)² - (x₂ - 2)².
To find the steepest ascent direction, we can take the gradient of the objective function with respect to x₁ and x₂. The gradient represents the direction of the steepest increase in the objective function. In this case, the gradient is given by (∂z/∂x₁, ∂z/∂x₂) = (-2(x₁ - 3), -2(x₂ - 2)).
Starting with initial values for x₁ and x₂, we can update their values iteratively by adding a fraction of the gradient to each variable. The fraction determines the step size or learning rate and should be chosen carefully to ensure convergence to the maximum value of z.
By repeatedly updating the values of x₁ and x₂ in the direction of steepest ascent, we can approach the solution that maximizes the objective function z. The process continues until convergence is achieved or a predefined stopping criterion is met.
Learn more about fraction here:
https://brainly.com/question/10354322
#SPJ11
rearrange the following so g is the main subject:
f+4(g-h)=x
Answers
Answer:
g=x-f+4h/4
Step-by-step explanation:
change of subject of formula
f+4(g-h)=x
f+4g-4h=x
4g-4h=x-f
4g=x-f+4h
g=x-f+4h/4
rate as brainliest
compute the orthogonal projection of onto the line through and the origin. The Orthogonal Projection Is
Answers
The orthogonal projection of [-2,2] onto the line passing through the origin and the point [-1,5] is the point [0.9231, 4.6154].
Orthogonal projection is a concept in linear algebra that allows us to find the closest point on a line to a given point.
To find the orthogonal projection of the point [-2,2] onto this line, we need to find the point on the line that is closest to the given point.
This line will be the line passing through the given point and perpendicular to the given line.
So, the projection of the given point [-2,2] onto the line passing through the origin and the point [-1,5] is given by the formula:
proj_l([-2,2]) = (([-2,2] . [-1,5]) / ([-1,5] . [-1,5])) x [-1,5]
where . represents the dot product of two vectors.
Evaluating this formula, we get:
proj_l([-2,2]) = (-12/26) x [-1,5]
proj_l([-2,2]) = [0.9231, 4.6154]
To know more about Orthogonal Projection here.
https://brainly.com/question/2292926
#SPJ4
Complete Question:
Compute the orthogonal projection of [-2 2] onto the line through [-1 5] and the origin.
The orthogonal projection is
two friends entered a contest jointly and won; however, there is only one prize and it cannot be split. some methods of selecting who receives the prize are given below. a: place both names in equal amounts into a hat and draw one without looking. b: ask a stranger to flip a coin. c: roll a die and evaluate the outcome as either even or odd. d: throw a stone closest to an object. e: play a hand of blackjack. f: ask a random stranger to select.
Answers
The methods that are fair include __A, B and C__ because __D__ is flawed due to increased chances of winning based on one's skill, ___F___ is flawed due to poor randomization, and ___E___ is flawed due to unequal probabilities of winning and losing.
Definition of ProbabilityProbability is a value used to measure the degree of occurrence of a random event. The word probability itself is often referred to as opportunity or possibility. Probability is generally the chance that something will happen.
The concept of probability has an important role in everyday life, starting from the scientific field, the government sector, the business or industry sector, to small issues such as entering the office or not due to thick clouds which are likely to rain heavily and flood .
In studying probability, there are three keywords that must be known namely experiments, outcomes and events or events.
For example, an experiment was conducted by asking 100 readers whether they would take a course in statistics or calculus. From this experiment there will be several possible outcomes. For example, the first possible outcome is that as many as 58 people will take any course. Another possible outcome is that 75 people are taking a calculus course and the rest are taking a statistics course. Another example of an experiment is the tossing of a dice. The result (outcome) of throwing a dice is likely to come out with one or two or three seeds and so on. The collection of these outcomes is known as an event.Learn more about probability model at https://brainly.com/question/29251028.
#SPJ4
solve the linear system using elimination
4x - 3y = 8
5x - 2y = -11
Answers
Answer:X=-7 and y=-12
Step-by-step explanation:
The solution is in the file below


PLZ HELP ME!!! NO LINKS PLZ!!!!!!
The results of a survey of students' favorite food are organized in the frequency table below. What is the sum of all of the relative frequencies for all types of food?
Food Preferred Frequency
Pizza 10
Hamburger 6
Spaghetti 1
Hotdog 5
Taco 4
*THE ANSWER IS NOT 26*
Select one:
a. 0
b. 100
c. 1
Answers
Answer:
100
Step-by-step explanation:
because it seems right
Answer:
C. 1
Step-by-step explanation:
The sum of relative frequencies in a distribution always equals 1
A rancher has 3000 feet of fencing with which to construct adjacent, equally sized rectangular pens as shown in the figure above. What dimensions should these pens have to maximize the enclosed area?
Answers
The required dimensions of a rectangular rancher with perimeter for fencing, 3000 feet are equal the 500 feet and 375 feet at maximum area of 3,75,000 ft².
We have a rancher which to construct adjacent, equally sized rectangular pens with the fencing of 3000 feet. Suppose that the rancher need to be fenced in the way shown in the attached figure. Then, the perimeter is 4x + 3y = 3000
=> x \( =\frac{3000 - 3y}{4} \).
The area of rectangle is represented by A=L × W --(1) , where L and W are dimensions of rectangles. The total area will be A = 2× x × y --(2)
=> A = 2× (\(\frac{3000 - 3y}{4}\))× y
= ( \( 1500 - \frac{3y}{2} \))y
= \( 1500y - \frac{3y²}{2} \)
Now, differentiate above area function, with respect to y, and equate to 0, for determining the critical points on the graph, \(\frac{dA}{dy} \) = A'(y) =\( 1500 - \frac{6y}{2} \) = 0
=> y = \(\frac{1500}{3} = 500 \)
Also, x \( =\frac{3000 - 3× 500}{4} \).
\( =\frac{1500}{4} = 375 \).
Maximum area = 375 × 500 × 2 = 375000 ft². Hence, the dimensions that will give the maximum area are 500 feet and 375 feet.
For more information about dimensions, visit :
https://brainly.com/question/19819849
#SPJ4
Complete question : attached figure complete the question.

This question has two parts. First, answer Part A. Then, answer Part B.
Part A: A statement about rational numbers is shown.
The product of two negative rational numbers is greater than either factor. Is the statement always true, sometimes true, or never true? Explain your answer. Provide at least two examples to support your answer.
Part B: A different statement about rational numbers is shown. The product of two positive rational numbers is greater than either factor. Provide at least two examples to show that this statement is only sometimes true.
30 points reward
Answers
The statement is not always true.
The statement is only sometimes true.
We have,
Part A:
The statement "the product of two negative rational numbers is greater than either factor" is never true.
Let a = -1/2 and b = -1/3.
Then ab = (-1/2)(-1/3) = 1/6, which is less than both a and b.
Let c = -1/4 and d = -2/3.
Then cd = (-1/4)(-2/3) = 1/6, which is also less than both c and d.
Both of these examples demonstrate that the product of two negative rational numbers can be less than either factor and therefore the statement is not always true.
Part B:
The statement "the product of two positive rational numbers is greater than either factor" is sometimes true, but not always. To see why, consider the following examples:
Let e = 1/2 and f = 1/3.
Then ef = (1/2)(1/3) = 1/6, which is less than both e and f.
Let g = 2/3 and h = 3/4.
Then gh = (2/3)(3/4) = 1/2, which is greater than both g and h.
These examples demonstrate that the product of two positive rational numbers can be less than either factor (in the first example) or greater than both factors (in the second example).
Therefore, the statement is only sometimes true.
Thus,
The statement is not always true.
The statement is only sometimes true.
Learn more about rational numbers here:
https://brainly.com/question/24398433
#SPJ1
Is 6a-5=4a+9,6 A solution or not a solution?
Answers
6a-5=4a+9
Subtract 4a from each side
6a-4a-5=4a-4a+9
2a-5 = 9
Add 5 to each side
2a-5+5 = 9+5
2a = 14
Divide each side by 2
2a/2 = 14/2
a = 7
The solution to the equation is 7
a=6 is not a solution
6, 6, 6, 7, 10, 11, 12, 13, 14, 14, 14, 15, 16, 18, 18
Calculate the Mean Absolute Deviation (MAD) of the data set (Round off to the nearest tenth)
Answers
Answer:
4.2
Step-by-step explanation:
I'm not 100% sure, but I did the math and ended up with 4.2! I hope this helps!
PLEASE HURRY! You encounter the following statement and explanation when reviewing a report at your finance job: (14^0/14^3)^1/3=14^-2/3 They are equivalent because (14/14^3)^1/3=(14^-2)^1/3
You notice this statement and explanation in the report are wrong. explain why it is wrong and give the correct answer.
Answers
The expressions are not equal and the explanation is wrong because the index forms have different exponential values.
The correct answer is 14^-1/3
How to determine the correct optionEquivalent expressions are known as expressions that are the same solution but differ in the mode of their arrangement.
From the information given, we have the index forms;
(14^0/14^3)^1/3=14^-2/3
It is important to note that exponents with zero equals 1.
Then, we have that;
1/14^1/3 = 14 ^-2/3
Take the inverse of the exponent
14^-1/3 is not equal to 14^-2/3
Hence, the correct answer is 14^-1/3
Learn about equivalent expressions on:
https://brainly.com/question/15775046
#SPJ1
part 2 help? I’ll mark brainliest if correct

Answers
Answer:
Draw a line segment, say 5 cm long.
Below it draw a line segment 10 cm long, or whatever is twice the length!
Hope that helps!
Step-by-step explanation:
Which expression is equivalent to (x Superscript 27 Baseline y) Superscript one-third?
1. x Superscript 3 Baseline (Superscript 3 StartRoot y end root)
2. x Superscript 9 Baseline (Superscript 3 StartRoot y end root)
3. x Superscript 27 Baseline (Superscript 3 StartRoot y end root)
4. x Superscript 24 Baseline (Superscript 3 StartRoot y end root)
Answers
Answer:
B
Step-by-step explanation
i got a 100 on the quiz
The required equivalent expression to the given expression is x Superscript 9 Baseline (Superscript 3 StartRoot y end root). Option 2 is correct.
What is simplification?It is a technique in mathematics to operate and interpret the function to make the function or expression straightforward or more understandable is called simplifying and the process is called simplification.
Here,
the given expression,
(x Superscript 27 Baseline y) Superscript one-third = [x²⁷/y]¹/³
= [[x²⁷/³]/∛y
= x⁹/∛y = x Superscript 9 Baseline (Superscript 3 StartRoot y end root)
Thus, the required equivalent expression to the given expression is x Superscript 9 Baseline (Superscript 3 StartRoot y end root). Option 2 is correct.
Learn more about simplification here:
https://brainly.com/question/12501526
#SPJ6
what is the equivalent ratio of 26:7
Answers
Answer:
52 : 14
Step-by-step explanation:
multiply the numbers by 2
find the box's speed vf at 2.6 s after you first started pushing on it.
Answers
The box's speed vf at 2.6 seconds after you first started pushing it is 18.2 m/s.
To determine the box's speed vf at 2.6 seconds after you first started pushing it, we first need to find the acceleration of the box and then use that acceleration to calculate its velocity using the kinematic equation:
v_f = v_i + at
Where:
v_f is the final velocity of the box
v_i is the initial velocity of the boxa is the acceleration
t is the time
First, we can use the given information to find the acceleration of the box using the equation:
a = F / m
Where:
F is the force you applied to the boxm is the mass of the box
From the given values, we have:
F = 35 Nm = 5 kg
Substituting these values into the equation above, we get:a = 35 N / 5 kga = 7 m/s^2
Now that we have the acceleration of the box, we can use the kinematic equation above to find its final velocity:v_f = v_i + at
We are given that the box starts from rest (v_i = 0).
Substituting the values we have so far, we get:
v_f = 0 + (7 m/s^2) × (2.6 s)v_f = 18.2 m/s
Learn more about velocity at:
https://brainly.com/question/29110878
#SPJ11
What is the rule that describes the translation that maps ΔLMN onto ΔL'M'N?

Answers
Answer:
3 united right and 4 units down
Step-by-step explanation:
the shape with the quotes- also called primes- is the second shape
Find the solution set of the inequality 8 � − 8 ≤ − 72. 8x−8≤−72.8, x, minus, 8, is less than or equal to, minus, 72, point � xx
Answers
The solution to to log subscript 2 baseline (2 x cubed minus 8) minus 2 log subscript 2 baseline xx = 1x = 2x = 3x = 4 is 2 log₂ (x³ - 8) - 2 log₂ x = -2.
A logarithm expression is an expression in which the unknown value is expressed as the power to which a base number must be raised to produce a given number. For example, the equation log₂ 8 = 3 can be expressed as 2³ = 8.
A logarithm function is a type of mathematical function that calculates the logarithm of a given number. Logarithm functions are commonly used in mathematics, engineering, and science to simplify calculations. Logarithm functions can also be used to convert between different units of measurement.
Learn more about logarithm expression here:
brainly.com/question/29116454
#SPJ1
complete question:
What is the solution to log subscript 2 baseline (2 x cubed minus 8) minus 2 log subscript 2 baseline xx = 1x = 2x = 3x = 4.
Find the general solution of the given differential equation, and use it to determine how solutions behave as t→[infinity].
y′+6y=t+e−4t
solve for y=
and solutions converge to the function y=
Answers
The solutions for differential equations of converge to the function:
y = (t/6) + (1/24)\(e^{-4t}\)
The given differential equation is:
y' + 6y = t + \(e^{-4t}\)
This is a first-order linear differential equation in standard form:
y' + p(t)y = q(t)
where p(t) = 6 and q(t) = t + e^(-4t). To solve this differential equation, we first find the integrating factor, which is given by:
μ(t) = e^(∫p(t) dt) = e^(∫6 dt) = \(e^{6t}\)
Multiplying both sides of the differential equation by μ(t), we get:
\(e^{6t}\) y' + 6\(e^{6t}\) y = t\(e^{6t}\) + \(e^{2t}\)
The left-hand side is the product rule of the derivative of e^(6t) y:
(\(e^{6t}\) y)' = t\(e^{6t}\) +\(e^{2t}\)
Integrating both sides with respect to t, we get:
\(e^{6t}\)y = ∫(t\(e^{6t}\) + \(e^{2t}\)) dt = (t/6)\(e^{6t}\) + (1/24)\(e^{2t}\) + C
where C is an arbitrary constant of integration. Rearranging, we get the general solution:
y = (t/6) + (1/24)\(e^{-4t}\)+ C\(e^{6t}\)
where C is the constant of integration.
To determine how the solutions behave as t approaches infinity, we can examine the term containing the exponential function \(e^{6t}\) in the general solution. As t approaches infinity, the term \(e^{6t}\)approaches zero, so the solutions converge to the function:
y = (t/6) + (1/24)\(e^{-4t}\)
This means that the solutions approach a straight line with slope 1/6 as t gets very large. The exponential term becomes negligible in comparison to the linear term, so the behavior of the solutions is dominated by the linear term.
Differential equations are mathematical equations that involve derivatives of unknown functions. The general solution of a differential equation is a family of functions that satisfies the equation, with one or more parameters that can be determined using initial or boundary conditions.
In this problem, we are asked to find the general solution of a first-order linear differential equation and analyze the behavior of its solutions as t approaches infinity.
Know more about "Differential equations" here:-
https://brainly.com/question/11181117#
#SPJ11
Review the graph. On a coordinate plane, a parabola opens up and goes through (negative 2, 5), has vertex (0, 1), and goes through (2, 5). Another parabola opens to the right and goes through (8, 4), has vertex (negative 8, 0), and goes through (8, negative 4). Everything inside of the first parabola and above the second parabola within the first parabola is shaded. Which system of inequalities has the solution set shown in the graph?
Answers
Answer:
The value of h is h = -1.5
Step-by-step explanation:
The quadratic equation is represented by a parabola, the vertex form of the equation is y = a(x - h)² + k, where
(h , k) are the coordinates of its vertex point
a is the coefficient of x²
∵ The graph is a parabola opens up
∵ It has a vertex at (-1.5, 0)
∵ The vertex of the parabola is (h , k)
∴ h = -1.5 and k = 0
∵ The graph shows f(x) = (x - h)²
∵ The coordinates of the vertex are (h , k)
∵ h = -1.5 and k = 0
∴ h = -1.5
The value of h is h = -1.5
The value of h is h = -1.5
We have given that,
On a coordinate plane, a parabola opens up and goes through (negative 2, 5), has vertex (0, 1), and goes through (2, 5). Another parabola opens to the right and goes through (8, 4), has vertex (negative 8, 0), and goes through (8, negative 4).
The quadratic equation is represented by a parabola,
What is the vertex form of the parabola?The vertex form of the equation is y = a(x - h)² + k, where
(h, k) are the coordinates of its vertex point
a is the coefficient of x²
∵ The graph is a parabola that opens up
∵ It has a vertex at (-1.5, 0)
∵ The vertex of the parabola is (h , k)
∴ h = -1.5 and k = 0
∵ The graph shows f(x) = (x - h)²
∵ The coordinates of the vertex are (h, k)
∵ h = -1.5 and k = 0
∴ h = -1.5
The value of h is h = -1.5.
To learn more about the vertex form of parabola visit:
https://brainly.com/question/17987697
#SPJ2
Is this equation in standard form?
3xy+ y2=4
Answers
Answer:
standard form is {Ax+By=c}
as mentioned above the given equation is not in {Ax+By=c}..
hence it's not in standard form
Answer:
ax+by=c so no
Step-by-step explanation:
if you buy a computer game for $54, you have a $5 mail-in rebate, and you pay 8% sales tax, how much does your game cost?
Answers
Answer:53.32
Step-by-step explanation:
$54 retail price
sales tax 8%
$54x8%= 4.32
sales tax is $4.32
$54+$4.32= $58.32
total with tax is $58.32
$58.32-$5= 53.32
what is 5.136 rounded to the nearest tenth
Answers
Answer:
5.136 is 5.1 to the nearest tenth
Evaluate the expression when x=4
9x
Answers
x=4x9
x=36x
So to answer this then it’s x=36 unless it’s different
x
=
4
⋅
9
x
=
3
6
Answer:
36
Step-by-step explanation:
Since x = 4, the question is asking you to replace the "x" in the expression with "4". Once you have made this substitution, you can see the the "9" and "4" are directly next to each other. This means that they should be multiplied together. Therefore, when x = 4, the value of the expression is be 36.
9x ----> 9(4) ----> 36
A composite wall consists of material A (thickness =15 cm,k A =10 W/m ∘ C ) and material B (thickness =20 cm,k B =16 W/m ∘ C ). The exposed surface of A is in contact with a hot fluid at 150 ∘ C (heat transfer coefficient =180 W/m 2∘ C ), and that of B is in contact with air at 38 ∘C (film coefficient =26 W/m 2∘C ). The mid-plane temperature of A (i.e. 7.5 cm away from the exposed surface) at steady state is measured to be 130 ∘C. (a) Is there any contact resistance at the junction of A and B ? If so, what is its magnitude? (b) Calculate the temperature jump at the interface. (c) If there was no contact resistance, by what per cent the thickness of slab A should have been increased to get the same heat flux (keeping the thickness of slab B unchanged)?
Answers
(a) Yes, there is a contact resistance at the junction of materials A and B. Its magnitude is 0.0384 m^2∘C/W.
(b) The exact temperature jump at the interface cannot be calculated without the surface area of the interface.
(c) If there was no contact resistance, the thickness of slab A should be increased to maintain the same heat flux, but the percentage increase cannot be determined without the surface area information.
(a) Yes, there is a contact resistance at the junction of materials A and B. Its magnitude can be determined using the equation for thermal resistance at the contact interface:
R_contact = (1 / h_interface) - (1 / h_A)
where R_contact is the contact resistance, h_interface is the heat transfer coefficient at the interface, and h_A is the heat transfer coefficient for material A. Substituting the given values:
R_contact = (1 / 26) - (1 / 180) = 0.0384 m^2∘C/W
(b) The temperature jump at the interface can be calculated using the equation:
ΔT_interface = Q / (h_interface × A_interface)
where ΔT_interface is the temperature jump, Q is the heat transfer rate, h_interface is the heat transfer coefficient at the interface, and A_interface is the surface area of the interface. As the area of the interface is not provided, we cannot calculate the exact value of ΔT_interface.
(c) If there was no contact resistance, the thickness of slab A would need to be increased to achieve the same heat flux. The heat flux (q) can be calculated using the equation:
q = (T_hot - T_cold) / (R_total)
where T_hot is the temperature of the hot fluid, T_cold is the temperature of the air, and R_total is the total thermal resistance of the composite wall. The total thermal resistance is the sum of the resistances of materials A and B and the contact resistance:
R_total = R_A + R_contact + R_B
To maintain the same heat flux, we can equate the two expressions for q and solve for the new thickness of slab A, denoted as t_A':
q = (T_hot - T_cold) / (R_A + R_contact + R_B)
q = (T_hot - T_cold) / (k_A × A_A / t_A' + R_contact + k_B × A_B / t_B)
where t_A' is the new thickness of slab A, A_A and A_B are the surface areas of materials A and B, and t_B is the thickness of slab B.
To solve for t_A', we rearrange the equation:
k_A × A_A / t_A' = q × (R_A + R_contact + R_B) - k_B × A_B / t_B
t_A' = k_A × A_A / (q × (R_A + R_contact + R_B) - k_B × A_B / t_B)
Substituting the given values and the previously calculated contact resistance:
t_A' = (10 × A_A) / (q × (0.15 + 0.0384 + 0.2) - 16 × A_B / 0.2)
Note: The values of A_A and A_B are not provided, so the final percentage increase in thickness cannot be calculated without that information.
To know more about thermal resistance and heat transfer, refer here:
https://brainly.com/question/33495792#
#SPJ11
which of the following is a difference between panel and pooled cross-sectional data? group of answer choices a panel data set consists of data on different cross-sectional units over a given period of time while a pooled data set consists of data on the same cross-sectional units over a given period of time. a panel data set consists of data on the same cross-sectional units over a given period of time while a pooled data set consists of data on different cross-sectional units over a given period of time a panel data consists of data on a single variable measured at a given point in time while a pooled data set consists of data on the same cross-sectional units over a given period of time. a panel data set consists of data on a single variable measured at a given point in time while a pooled data set consists of data on more than one variable at a given point in time.
Answers
From the following, a panel data set consists of data on the same cross-sectional units over a given period of time while a pooled data set consists of data on different cross-sectional units over a given period of time is the difference between panel and pooled cross-sectional data.
Panel data refers to samples of the same cross-sectional units observed at multiple points in time.
For example we will follow the same set of households X, Y and Z, for each time period we collect data i.e. in 1990 and we will also interview the same households in 1995.
Pooled data occur when we have a “time series of cross sections,” but the observations in each cross section do not necessarily refer to the same unit.
For example we will take household income data on households X, Y and Z, in 1990. And then we will take the same income data on households G, F and A in 1995. Although we are interested in the same data, we are taking different samples (using different households) in different time periods.
To know more about panel data
https://brainly.com/question/30657393
#SPJ4
Mrs. Hernandez was helping her students with their bank accounts. The ratio of the amount of the student with the most money to the student with the least money was 4:1. If the student with the most money has $128, how much does the student with the least money have
Answers
Answer: $32
Step-by-step explanation:
From the information given in the question, we are told that the ratio of the amount of the student with the most money to the student with the least money was 4:1. If the student with the most money has $128.
This shows that the student with most money has quadruple that is 4× the student with the least money. Therefore, the student will least money will have:
= $128/4
= $32