The line y = 3x - 6 is dilated by the scale factor k=3 and centered at the origin. What is the equation of the new
line
I’ll give brainliest
Answers
The equation of the new line, after dilation by a scale factor of 3 and centering at the origin, is y' = 9x - 18.
To dilate a line by a scale factor of k and center it at the origin, you multiply the coordinates of each point on the original line by the scale factor. Since the given line is y = 3x - 6, we can perform the dilation as follows:
The original line: y = 3x - 6
To dilate it by a scale factor of 3, we multiply both the x-coordinate and the y-coordinate of each point by 3:
New line: y' = 3 * y and x' = 3 * x
Substituting these values into the original equation, we have:
y' = 3(3x - 6)
Simplifying, we get:
y' = 9x - 18
Therefore, the equation of the new line, after dilation by a scale factor of 3 and centering at the origin, is y' = 9x - 18.
Learn more about equation here
https://brainly.com/question/17145398
#SPJ11
Related Questions
find the degree of the monomial -3q^4rs^6
Answers
Answer:
11
Step-by-step explanation:
q^4=4
r=1
s^6=6
4+1+6=11
HELP FIND SURFACE AREA OF PYRAMID

Answers
Answer:
Figure 1: 623.2 in²
Figure 2: 679.8 in²
Step-by-step explanation:
For a pyramid total surface area
= Base Area + Lateral Surface Area
Figure 1 is a triangular prism
It's base is an equilateral triangle with side = 20 in
Area of an equilateral triangle = \(\dfrac{\sqrt{3}}{4} a^2\) where \(a\) is the length of the base
So in figure 1, base area = area of equilateral triangle with side a = 20 in
\(\text{Base Area =} \dfrac{\sqrt{3}}{4} \cdot 20^2 \approx 173.2 \;in^2\)
Each lateral side is an isosceles triangle with base = 20 and height = 15
Area of each triangle
\(= \dfrac{1}{2} \cdot base \cdot height\)
\(= \dfrac{1}{2} \cdot 20 \cdot 15 \\\\= 150 \; in^2\)
There are three such lateral sides so total lateral area = 150 x 3 = 450 in²
Total surface area = 173.21 + 450 = 623.2 in²
Figure 2
This is a regular hexagonal pyramid
The base is a regular hexagon of side 10
Base area = Area of hexagon of side 10
Area of a regular hexagon with side a
\(= \dfrac{3\sqrt{3}}{4} a^2\)
Base area of Figure 2
\(= \dfrac{3\sqrt{3}}{4} 10^2\\\\\approx 259.8 \;in^2\)
The lateral surface consists of 6 isosceles triangles each with a base = 10 in and height = 14 in
Area of each isosceles triangle
\(= \dfrac{1}{2} \cdot 10 \cdot 14 \\\\= 70 \;in^2\)
Since there are 6 such lateral triangles, total lateral surface area
= 70 x 6 = 420 in²
So total surface area = base area + total lateral surface area
= 259.8 + 420 = 679.8 in²
Which situation is modeled by the equation 24 = 15x + 8?

Answers
Help me or give me answer key plz asap

Answers
Hello, this should help you out!
In this graph, the y values move up 3 units each. Therefore, the blue parabola underwent a translation of 3 units upward.
For further explanation, we see that (0,0) goes up to (0,3), meaning the graph shifted upwards 3 units. So, each y value is raised by positive 3 units!
I hope I was of assistance! #SpreadTheLove! <3
How do you identify the vertical and horizontal asymptotes for rational functions?
Answers
To identify the vertical asymptotes, we have to factor the denominator. For horizontal asymptotes, we compare the degrees of the numerator and denominator.
For rational functions, there are vertical and horizontal asymptotes. To identify the vertical asymptotes, we first have to factor the denominator. After that, we should look for values that make the denominator zero. These values can be found by setting the denominator equal to zero and solving for x. The resulting x values would be the vertical asymptotes of the function.
The horizontal asymptote is the line that the function approaches as x goes towards infinity or negative infinity. For rational functions, the horizontal asymptote is found by comparing the degrees of the numerator and the denominator.
If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is y = 0. If the degree of the numerator is equal to the degree of the denominator, the horizontal asymptote is y = the ratio of the leading coefficients. If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote.
To know more about the vertical asymptotes visit:
https://brainly.com/question/31315562
#SPJ11
Here are the result of three experiments where the measure of the two groups being compared are exactly the same but the standard deviation is quite different from experiment to experiment. Compute the effect size using the formula on page 179 and then discuss why this size changes as a function of the change in variability. EFFECT SIZE 78.6 EXPERIMENT 1 MEAN GROUP 1 MEAN GROUP 2 STANDAR DEVIATION 73.4 EXPERIMENT 1 MEAN GROUP 1 MEAN GROUP 2 STANDAR DEVIATION 78.6 73.4 EXPERIMENT 1 MEAN GROUP 1 MEAN GROUP 2 STANDAR DEVIATION 78.6 73.4 ES - X, - SD where ES = effect size Ž, = the mean for Group 1 X, = the mean for Group 2 SD= the standard deviation from either group
Answers
To compute the effect size, we can use the formula:
ES = (|Ž - X|) / SD
where Ž is the mean for Group 1, X is the mean for Group 2, and SD is the standard deviation from either group as the given question.
How we measure the Standard deviation and effect size?Using the given values, we have:
Experiment 1: ES = (|78.6 - 73.4|) / 2 = 2.6
Experiment 2: ES = (|78.6 - 73.4|) / 4 = 1.3
Experiment 3: ES = (|78.6 - 73.4|) / 8 = 0.65
From the experiments 1, 2, 3, we can see that the standard deviation increases, the effect size decreases.
It means that the larger SD makes it harder to detect a meaningful difference between the two groups.
To know more about standard deviation, visit: https://brainly.com/question/475676
#SPJ1
Help! It’s slope-Intercept form:Write an equation from a table

Answers
Answer:
the answer would be f(x)=-5x+41
Step-by-step explanation:
you start by calculating the change in y (or f(x)) and dividing that by the change in x or y2-y1/x2-x1. the answer you should get is the slope (mx). from there you calculate the y intercept (b) by simply finding when x=0. now you put it all together, y=mx+b or f(x)=-5x+41
41-36= -5
The difference or the slope is -5 because we are subtracting by 5.
(0,41) 41 is your y intercept
y=-5x+41
A fair six sided die (sides of 1,2,3,4,5, and 6, and each side is equally likely) is to be thrown 5 (five) times. The throws are independent of one another. What is the probability that you roll an even number in at least one of the throws
Answers
The probability of rolling an even number in at least one of the throws is 31/32 or approximately 0.969.
The probability of not rolling an even number in a single throw is 1/2, since there are three odd numbers and three even numbers on the die. Therefore, the probability of not rolling an even number in five independent throws is (1/2)^5 = 1/32.
The probability of rolling an even number in at least one of the throws is the complement of the probability of not rolling an even number in any of the five throws. So:
P(rolling an even number in at least one of the throws) = 1 - P(not rolling an even number in any of the five throws)
= 1 - (1/32)
= 31/32
Therefore, the probability of rolling an even number in at least one of the throws is 31/32 or approximately 0.969.
for such more question on probability
https://brainly.com/question/13604758
#SPJ11
I need help cancelling units

Answers
Answer:
60:1
Step-by-step explanation:
60:1 = 366:x
60x = 366
x = 6.1
366 minutes is equivalent to 6.1 hours.
Convert 366 minutes to hours.
Knowing that in 60 minutes = 1 hour.\(\boldsymbol{\sf{Therefore \ \to \ 366 \not{m}*\dfrac{1 \ hr}{60\not{m}}=6.1 \ hr }}\)
We conclude that a time of 366 minutes is equal to 6.1 hours
There are 60 minutes in 1 hour. To convert from minutes to hours, divide the number of minutes by 60. For example, 120 minutes equals 2 hours because 120/60=2.
Which expressions are equivalent to x + 2y + x + 2
Answers
Answer:
Where are the expressions??
Step-by-step explanation:
x + 2y + x + 2 simplified would be 2x+2y+2
Hope this helps :)
A car travels a distance of 230 miles in a time of 4.2 hours. What is its average speed rounded to 1dp?
Answers
\( \large \sf \underline \bold { \color{violet}Given :}\)
Total Distance Traveled = 230 miles.Time Taken In Travel = 4.2 hours.\( \large \sf \underline \red{Now, \: By \: Avarage \: Speed \: = \frac{Distance}{Time} }\)
\( \large \sf = \frac{230}{4.2} \)\( \large \boxed{ \sf \orange{54.76 \: m/h}}\)Hope It's Helps!Its average speed rounded to 1dp is 54.76 miles per hour.
Average speedUsing this formula
Average speed=Distance/Time
Where:
Total Distance =230 miles
Time= 4.2 hours
Let plug in the formula
Average speed=230/4.2
Average speed=54.76
Inconclusion Its average speed rounded to 1dp is 54.76 miles per hour.
Learn more about average speed here:https://brainly.com/question/4931057
an experimenter surveyed two acres of a desert preserve and found six cactus wren nests. assuming that the habitat is fairly uniform, how many nests would he expect to be in the entire 200-acre preserve?
Answers
600 cactus wren nests the experimenter would expect to be in the entire 200-acre preserve.
To estimate the number of cactus wren nests in the entire 200-acre preserve, we can use the ratio of the area surveyed to the number of nests found.
Let's call the number of nests in the entire 200-acre preserve "N".
The ratio of the area surveyed to the number of nests found is:
2 acres / 6 nests = 200 acres / N nests
We can use this ratio to find the number of nests in the entire 200-acre preserve:
N nests = 200 acres * (6 nests / 2 acres)
N nests = 200 * 3
N nests = 600
So the experimenter would expect to find approximately 600 cactus wren nests in the entire 200-acre preserve, assuming that the habitat is fairly uniform.
You can learn more about habitat at
https://brainly.com/question/20319955
#SPJ4
A college plans to interview 6 students for possible offer of graduate assistantships. The college has three assistantships available. How many groups of three can the college select
Answers
The college can select 20 groups of three students from the six interviewees for graduate assistantships.
A college plans to interview 6 students for possible offer of graduate assistantships. The college has three assistantships available.
The number of ways in which a college can select three students from the six interviewees for graduate assistantships can be calculated by the combination formula:
C(n, r) = (n!) / [(n - r)! r!],
where n = number of interviewees = 6 and r = number of graduate assistantships available = 3.
C(6, 3) = (6!) / [(6 - 3)! 3!]
C(6, 3) = (6 x 5 x 4 x 3!) / [(3 x 2 x 1) x (3 x 2 x 1)]
C(6, 3) = 20
Therefore, the college can select 20 groups of three students from the six interviewees for graduate assistantships.
Learn more about "Combination" : https://brainly.com/question/28065038
#SPJ11
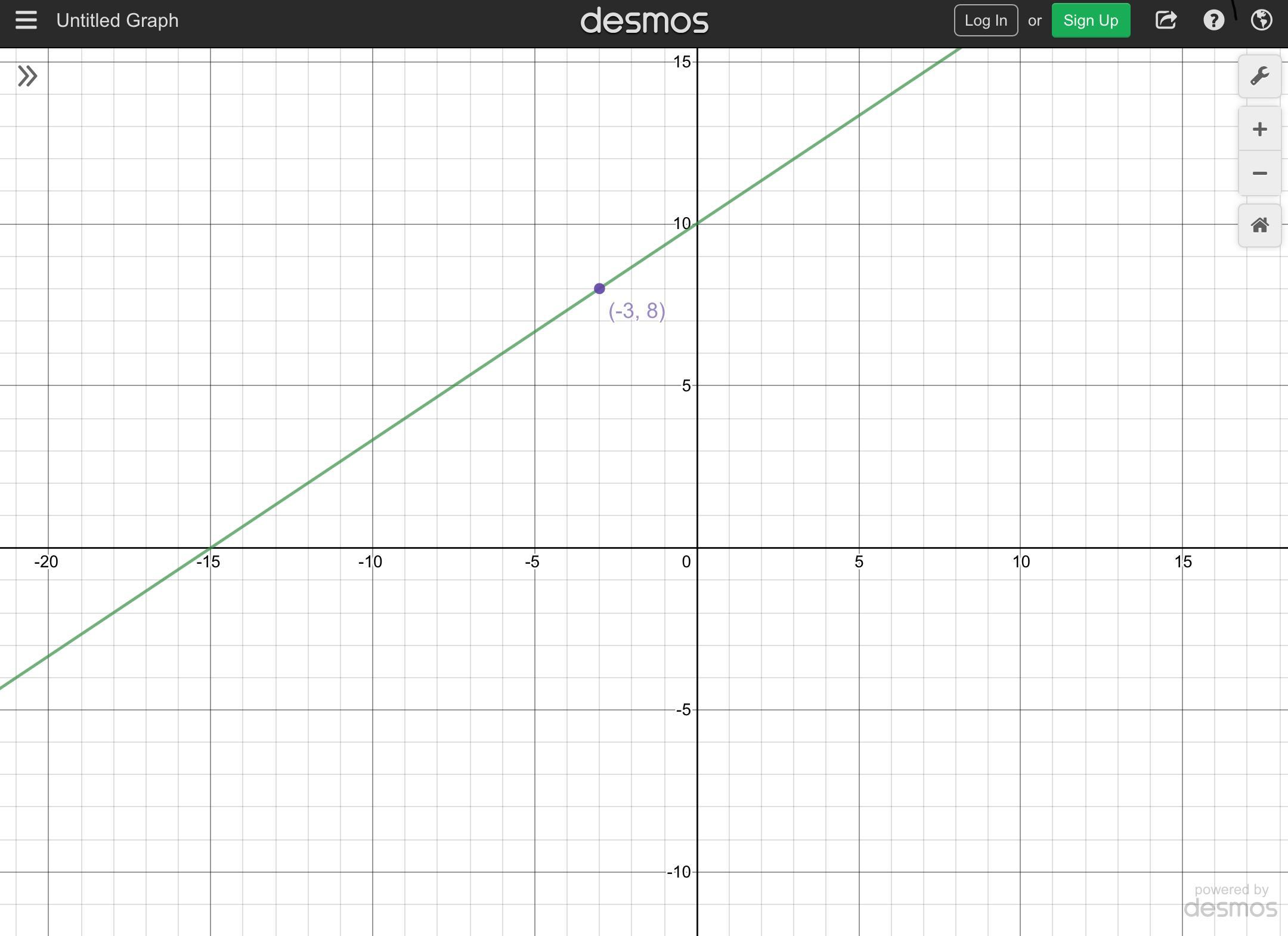
Help please!!! I messed up on the first question I asked, but this one is right!

Answers
Answer:
1) m=2/3
2) b=10
3) x-int:(-15, 0)
4) y-int: (0, 10)
Our equation is:
\(y=\frac{2}{3}x+10\)
Step-by-step explanation:
To start, let’s find the equation of the line.
We can use the point-slope form:
\(y-y_1=m(x-x_1)\)
Where m is the slope and (x₁, y₁) is a point.
So, let’s substitute 2/3 for m and (-3, 8) for (x₁, y₁). This yields:
\(y-8=\frac{2}{3}(x-(-3))\)
Simplify:
\(y-8=\frac{2}{3}(x+3)\)
Distribute:
\(y-8=\frac{2}{3}x+2\)
Add 8 to both sides:
\(y=\frac{2}{3}x+10\)
This is in slope intercept form: y=mx+b.
Therefore, our m is 2/3 and our b is 10.
To find the x-intercept, we will substitute 0 for y and solve for x. Therefore:
\(0=\frac{2}{3}x+10\)
Subtract 10 from both sides:
\(-10=\frac{2}{3}x\)
Multiply both sides by 3/2. So:
\(x=-10(\frac{3}{2})=-30/2=-15\)
Therefore, the x-intercept is (-15, 0).
To find the y-intercept, we will substitute 0 for x and solve for y. Therefore:
\(y=\frac{2}{3}(0)+10=10\)
So, the y-intercept is (0, 10).
We will also graph it. See the attachment. To graph by hand, we can start at the y-intercept and go up two for every three to the right. Or, we can go down two for every three to the left. This should yield the following graph:
a random group of high school and college students were asked if they study with or without listening to music. the frequency table below shows the results of the poll. a 4-column table with 3 rows. the first column has no label with entries high school, college, total. the second column is labeled music with entries 68, 85, 153. the third column is labeled no music with entries 65, 51, 116. the fourth column is labeled total with entries 133, 136, 269. which statements are true? check all that apply. the table shows conditional relative frequencies by column. the table shows conditional relative frequencies by row. the conditional relative frequency that someone is in high school, given that the person prefers to study without music, is about 0.56. if someone prefers to study with music, the probability the person is in college is about 63%. if someone prefers to study with music, the probability the person is in hs is about 44%.
Answers
Answer:
The conditional relative frequency that someone is in high school, given that the person prefers to study without music, is about 0.56.
If someone prefers to study music, the probability the person is in HS is about 44%.
Step-by-step explanation:
In the music column, we see that
total people who prefer to study with music = 153
high school students = 68
So, probability of high school students who study with music
= 68/153
= 0.44
= 44%.
College students = 85
Probability of college students who prefer to study with music
= 85/153
= 0.56
= 56%.
So, the correct statements are :
The conditional relative frequency that someone is in high school, given that the person prefers to study without music, is about 0.56.
If someone prefers to study with music, the probability the person is in HS is about 44%.
Answer:
3 and 5
Step-by-step explanation:
2022
which of the following square roots would not be between 4 and 5?
Answers
Answer:
√10.
___________________
Step-by-step explanation:
As you have not provided any options, the correct answer would be a value NOT between :
\(\sqrt{4}\) and \(\sqrt{5}\)
Or in decimal, between:
2 and 2.236
Hope this helps!
Scott’s family has cats and birds as pets. Scott counted the total number of legs his pets have. Scott counted 30 legs total. If Scott’s family owns 3 birds, how many cats do they own?
Show how you solved it!!!!
I need this as soon as possible!
Answers
3birds would have=2(3)=6legs
Cats have:-
30-6=24legsEach cat has 4legs.
Total cats:-
\(\\ \sf\longmapsto \dfrac{24}{4}=6cats\)
alice ate 5 cookies and 2 carrots for a total of 590 calories; bob ate 3 cookies and 4 carrots for a total of 410 calories. how many calories are in one cookie?
Answers
Since, Alice ate 5 cookies and 2 carrots for a total of 590 calories; bob ate 3 cookies and 4 carrots for a total of 410 calories. Therefore, In a cookie there are 110 calories.
A calorie is a unit of energy that food and drink provide. we can usually find out how many calories are listed in foods, and wearables like the best fitness trackers let you monitor how many calories you're burning in different activities. Certain foods, such as processed foods, tend to be high in calories. Other foods, such as fresh fruits and vegetables, tend to be low in calories. there is not. Calories are needed to give you enough energy to move, keep warm, grow, work, think, and play. Our circulation and digestion also need to work well with the energy we get from calories.
Let x = calories in cookies.
y = calories in carrots.
Now, according to the question:
5x + 2y = 590 --------------------------------------- (1)
3x + 4y = 410 -------------------------------------- (2)
Multiplying equation(1) by 3 and equation(2) by 5:
15x + 6y = 1770 ---------------------------(3)
15x + 20y = 2050 ---------------------------(4)
Solving we get:
y = 280/14
or, y = 20 units.
Putting the value of y = 20 in equation (2)
3x + 4y = 410
⇒ 3x + 4 × 20 = 410
⇒ 3x = 410 - 80
⇒ x = 330/3
⇒ x = 110 Units
Therefore, the calories of cookies is 110 units .
Learn more about Calories:
https://brainly.com/question/17078881
#SPJ4
2. A cell phone costs $600 and is on sale for 25% off. What is the sale price after the discount?
whole
Type your answer in the box below.
The sale price after the discount is $
100
or part=% x whole
Answers
The sale price of the cell phone that costs $600, after a 25% discount from the cost is $450
What is a discount?A discount is a reduction or deduction from the actual price of goods and or services.
The cost of the cell phone = $600
The percentage discount on the of the cell phone = 25%
The sale price after the discount can therefore be calculated as follows;
Sale price = ((100 - 25)/100) × $600 = $450
The sale price after the discount = $450
Learn more on percentage discount here: https://brainly.com/question/13501493
#SPJ1
Find the value of x that makes the equation true.
2[x + (2 1/2 + 2x )] = -3 (x - 1 ) + 9
Answers
Answer:
x = 7/9 or 0.78 as a decimal
Step-by-step explanation:
have a nice day!! :)
Suppose IQ scores were obtained for randomly selected sets of . The pairs of measurements yield , , r , P-value 0.000, and , where x represents the IQ score of the . Find the best predicted value of given that the has an IQ of ?
Use a significance level of 0.05. 20 siblings 20 x=99.42 y=97.2 =0.867 = = −21.33+1.19x y older child y older child 97 Click the icon to view the critical values of the Pearson correlation coefficient r.1 The best predicted value of is . y (Round to two decimal places as needed.) Critical Values of the Pearson Correlation Coefficient r n 0.05 α = 0.01 α = NOTE: To test H0 : 0 against H1: 0, reject H0 if the absolute value of r is greater than the critical value in the table. rho= rho≠4 0.950 0.990 5 0.878 0.959 6 0.811 0.917
Answers
The best predicted value given that a person has an IQ of 91 is 94.03.
Here, we are given that-
sample size n = 20
sample mean for the independent value x = 100.39
sample mean for the dependent value y = 103.6
coefficient of correlation r = 0.925
The general expression for representing a linear model is given by-
y = β₀ + β₁x
where β₀ is the intercept and β₁ is the slope
For the above given case, the linear model will be given as-
y = -3.34 + 1.07x
where -3.34 is the intercept and 1.07 the slope.
To find the best predicted value when X = 91, we substitute the value of x as 91 in the equation as follows-
y = -3.34 + 1.07(91)
y = 94.03
Thus, the best predicted value given that a person has an IQ of 91 is 94.03.
Learn more about estimation here-
https://brainly.com/question/15712887
#SPJ4
Can y’all help with this? (It’s exponential and decaying factors). Thanks!!

Answers
Answer:
2.37×10^-11 milliliters
Step-by-step explanation:
The exponential model for decay is ...
y = a·b^x
where 'a' is the initial value, 'b' is the decay factor, and x is the number of intervals over which the decay is taking place.
__
Here, you're given an initial value of a=500 mL.
The decay factor is 1 more than the decay rate, so is ...
b = 1 -12% = 0.88
We are asked for the remaining amount after 240 intervals (breaths), so that will be ...
y = 500·0.88^x
y = 500·0.88^240 ≈ 2.37×10^-11 . . . . milliliters
__
Additional comment
That's about 640 million molecules of air--not very much. After 400 breaths, there is about 1 molecule of the original air remaining.
Find the value of x from the figure
please answer fast

Answers
Step-by-step explanation:
hope it helps you


how to change decimals to percentages
Answers
You move the decimal point over 2 spots to the right.
For example, the value 0.03 becomes 3%
Another example: 0.789 turns into 78.9%
Moving the decimal over 2 spots to the right is the same as multiplying by 100
The following gives the number of accidents that occurred on Florida State Highway 101 during the last 4 months:
Month
Jan
Feb
Mar
Apr
Number of Accidents
30
40
60
95
Using the
least-squares regression method, the trend equation for forecasting is (round your responses to two decimal places)
y= _____+_____x
Using least-squares regression, the forecast for the number of accidents that will occur in the month of May = accidents (enter your response as a whole number).
Answers
The forecast for the number of accidents that will occur in the month of May is 110.
To find the trend equation for forecasting using the least-squares regression method, we need to perform a linear regression analysis on the given data.
Let's assign the variable x to represent the month number (1 for Jan, 2 for Feb, etc.) and y to represent the number of accidents.
Using the given data:
x: 1, 2, 3, 4
y: 30, 40, 60, 95
Step 1: Calculate the means of x (bar) and y (bar):
x(bar) = (1 + 2 + 3 + 4) / 4 = 2.5
y(bar) = (30 + 40 + 60 + 95) / 4 = 56.25
Step 2: Calculate the deviations from the means (dx and dy):
dx = x - x(bar)
= 1 - 2.5, 2 - 2.5, 3 - 2.5, 4 - 2.5
= -1.5, -0.5, 0.5, 1.5
dy = y - ȳ = 30 - 56.25, 40 - 56.25, 60 - 56.25, 95 - 56.25
= -26.25, -16.25, 3.75, 38.75
Step 3: Calculate the product of the deviations (dxdy):
dxdy = dx * dy
= (-1.5) * (-26.25), (-0.5) * (-16.25), 0.5 * 3.75, 1.5 * 38.75
= 39.375, 8.125, 1.875, 58.125
Step 4: Calculate the squared deviations (dx² and dy²):
dx² = dx * dx
= (-1.5) * (-1.5), (-0.5) * (-0.5), 0.5 * 0.5, 1.5 * 1.5
= 2.25, 0.25, 0.25, 2.25
dy² = dy * dy
= (-26.25) * (-26.25), (-16.25) * (-16.25), 3.75 * 3.75, 38.75 * 38.75
= 689.0625, 264.0625, 14.0625, 1503.125
Step 5: Calculate the sum of the squared deviations (Σdx² and Σdy²):
Σdx² = 2.25 + 0.25 + 0.25 + 2.25 = 5
Σdy² = 689.0625 + 264.0625 + 14.0625 + 1503.125 = 2470.3125
Step 6: Calculate the sum of the product of the deviations (Σdxdy):
Σdxdy = 39.375 + 8.125 + 1.875 + 58.125 = 107.5
Step 7: Calculate the slope (b):
b = Σdxdy / Σdx² = 107.5 / 5 = 21.5
Step 8: Calculate the y-intercept (a):
a = y(bar) - b * x(bar)
= 56.25 - 21.5 * 2.5
= 56.25 - 53.75
= 2.50
Therefore, the trend equation for forecasting is:
y = 2.50 + 21.50x
To find the forecast for the number of accidents in May (x = 5), substitute x = 5 into the equation:
y = 2.50 + 21.50 * 5
= 2.50 + 107.50
= 110
To know more about number visit:
brainly.com/question/3589540
#SPJ11
how does cuscuta plant derive it's nutrition
Answers
Step-by-step explanation:
The plant Cuscuta derives its nutrition from the host plant by sending its root-like structures into the stem or roots of the host plant to absorb water, mineral salts and food from it. This type of nutrition is known as Parasitic Nutrition.
Answer:
The plant Cuscuta derives its nutrition from the host plant by sending its root-like structures into the stem or roots of the host plant to absorb water, mineral salts and food from it. This type of nutrition is known as Parasitic Nutrition.
mathematics homework

Answers
The angles and arcs are as follows
5. Arc RS = < RQS
6. < 1 = arc AB
7. < KQL = arc KL
8. arc SVT = < SQT
9. 120/r
10. 123° r
How to find the length of arcthe length of arc, s on a circle is given by the formula
s = r θ
where
r = radius of the circle
θ = angle in radians
9. in the figure we have that
s = 120
θ = s / r
θ = 120/r
10.
θ = 120
s = 120r
Learn more about length of arc at:
https://brainly.com/question/2005046
#SPJ1
1. Corey is waiting at a bus stop for the Number 3 bus. If all the buses that use the bus stop are equally likely to come along, what is the probability that the next bus will be the Number 3 bus?
Answers
Using the data, estimate limits between which most of the 73,219 composite scores would fall. Also, estimate the proportion of the 73,219 composite scores that would be at least 42
Answers
Estimated proportion of the 73219 composite scores that would be at least 42 is 0.09823625 i.e. 0.10
Step-by-step explanation:
The observed data can be roughly classified as normally distributed data. We will compute a three-standard deviation interval that contains 99.73% of the values.
Assume that random variable X represents the customers' composite scores.
: X~N (u, σ² )
The parameters' exact values are unknown to us. These are estimated using observed sample values.
Estimated mean is given by
U=1/65 ∑ x^65=32
Estimated standard deviation is given by
σ=√1/64 ∑^65(x ^i -u)^2=7.741931
So, 3-standard deviation interval is given by
(u-3*σ, u-3 *σ)
=(32-3*7.741931+3*7.741931)
=(8.7742,55.2258)
The composite scores have integral values and cannot exceed 49. We must adjust the interval in light of these two facts..
So, most of the 73,129 composite scores would fall in the interval (8,49).
p(X>42)=P(X-u/σ>42-32/7.741931)
=p(Z>1.291667)
=0.09823625
Estimated proportion of the 73219 composite scores that would be at least 42 is 0.09823625 i.e. 0.10
To learn more about estimated composite values
https://brainly.com/question/17961193
#SPJ4
What is the proper expression for the absolute value of 3?
Answers
When we take the absolute value of a number, we always end up with a positive number (or zero). Whether the input was positive or negative (or zero), the output is always positive (or zero). For instance, | 3 | = 3, and | –3 | = 3 also.