Answers
Answer:
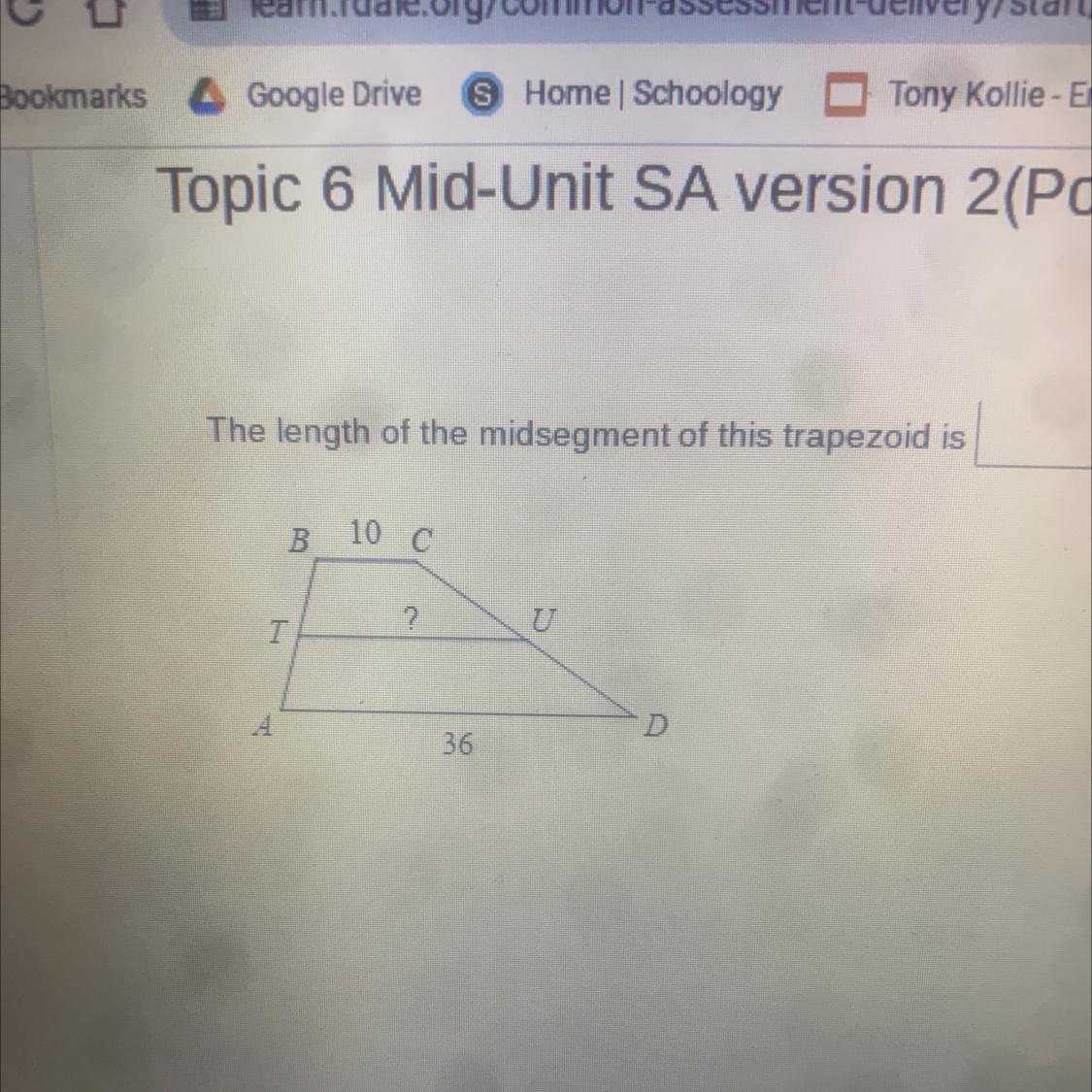
one-half
The midsegment of a trapezoid is parallel to each base, and its length is one-half the sum of the lengths of the bases
Related Questions
a parabola has a maximum value of 4 at x equals negative 1 and y intercept of 3 and an x-intercept of 1
Answers
ANSWER:
C.
STEP-BY-STEP EXPLANATION:
According to the statement, we know that the maximum point is (-1, 4) and that it has two intercepts (0, 3) and (1, 0).
The only graph that meets these characteristics is the following:

yasmine is playing a true false geography game. She has answered 15 of her 20 questions correctly. What is the probability that she will answer the five remaining questions correctly
Answers
Answer:
1/32
Step-by-step explanation:
Assuming that each question is independent, the probability of Yasmine answering a question correctly is 1/2, since each question has two possible answers (true or false) and she has a 50/50 chance of guessing correctly. Therefore, the probability of her answering all five remaining questions correctly is:
(1/2)^5 = 1/32
So the probability of Yasmine answering the five remaining questions correctly is 1/32, or approximately 0.03125, or about 3.125%.
Answer:
100%
Step-by-step explanation:
We know
She has answered 15 of her 20 questions correctly.
What is the probability that she will answer the five remaining questions correctly?
We take
15/15 = 100%
So, 100% she will answer the five remaining questions correctly.
Solve the system.
-5x - 6y = -17
-3x -5y + 5z = 2
-6x - 5y + z = -13
Enter your answer as an ordered triple.
(?, ?, ?)
Answers
The value of x, y and z in the system equation is (1, 2, 3).
What is the solution of the equation?The solution of the equation can be determined by using Cramer's rule as follows;
[-5 -6 0] = [ -17]
[-3 -5 5] [2 ]
[-6 -5 1] [-13 ]
The determinant of the matrix is calculate as;
Δ = -5 (-5 + 25) + 6(-3 + 30) + 0(15 + 30)
Δ = 62
The x-determinant of the matrix is calculated as follows;
Δx = -17(-5 + 25) + 6(2 + 65) + 0
Δx = 62
The y-determinant of the matrix is calculated as follows;
Δy = -5(2 + 65) + 17(-3 + 30) + 0
Δy = 124
The z-determinant of the matrix is calculated as follows;
Δz = -5(65 + 10) + 6 (39 + 12) - 17(15 - 30)
Δz = 186
The value of x, y and z is calculated as follows;
x = Δx/Δ = 62/62 = 1
y = Δy/Δ = 124/62 = 2
z = Δz/Δ = 186/62 = 3
Learn more about system equations here: https://brainly.com/question/13729904
#SPJ1
The legend on a map states that 1 inch is 20 miles. If you measure 5 inches on the map, how many miles would the actual distance be? Actual distance = [ ? ] miles
Answers
Answer:
1 inch= 20 miles. 5*20=100 miles. The answer is 100 miles.
Step-by-step explanation:
On these types of questions just do that every time, then you don't need to ask, for example:
1 foot = 50 miles
If it measures 3 feet.
3*50=150 miles.
If you have any questions regarding my answer, tell me in the comments, and I will answer them.
Use the histogram to answer the following questions.
Frequency
The frequency of the class 90-93 is
The frequency of the class 94-97 is
This means that a total of
5.5
5
4.5
Your answers should be exact numerical values.
The frequency of the class 86-89 is
86
94
90
Duration of Dormancy (minutes)
dormancy periods were recorded.
Answers
The parameters that are needed to calculate a probability are listed as follows:
Number of desired outcomes in the context of a problem or experiment.Number of total outcomes in the context of a problem or experiment.Then the probability is calculated as the division of the number of desired outcomes by the number of total outcomes, hence it is the same as a relative frequency.
The total number of periods is given as follows:
5 + 6 + 4 = 15.
The frequency of each class is given as follows:
86 - 89: 5/15 = 1/3.90 - 93: 6/15 = 2/5.94 - 97: 4/15.Learn more about the concept of probability at https://brainly.com/question/24756209
#SPJ1

A) Find an equation for the line perpendicular to the tangent line to the curve y=x^3-4x+6 at the point (2,6)
-The equation is y=
b) What is the smallest slope on the curve? At what point on the curve does the curve have this slope?
-The smallest slope on the curve is
-The curve has the smallest slope at the point
c) Find equations for the tangent lines to the curve at the points where the slope of the curve is 8.
Answers
Answer:
f(x) = x³ - 4x + 6
f'(x) = 3x² - 4
a) f'(2) = 3(2²) - 4 = 12 - 4 = 8
6 = 8(2) + b
6 = 16 + b
b = -10
y = 8x - 10
b) 3x² - 4 = 0
3x² = 4, so x = ±2/√3 = ±(2/3)√3
= ±1.1547
f(-(2/3)√3) = 9.0792
f((2/3)√3) = 2.9208
c) 3x² - 4 = 8
3x² = 12
x² = 4, so x = ±2
f(-2) = (-2)³ - 4(-2) + 6 = -8 + 8 + 6 = 6
6 = -2(8) + b
6 = -16 + b
b = 22
y = 8x + 22
f(2) = 6
y = 8x - 10
The equation perpendicular to the tangent is y = -1/8x + 25/4
-The smallest slope on the curve is 2.92
The curve has the smallest slope at the point (1.15, 2.92)
The equations at tangent points are y = 8x + 16 and y = 8x - 16
Finding the equation perpendicular to the tangentFrom the question, we have the following parameters that can be used in our computation:
y = x³ - 4x + 6
Differentiate
So, we have
f'(x) = 3x² - 4
The point is (2, 6)
So, we have
f'(2) = 3(2)² - 4
f'(2) = 8
The slope of the perpendicular line is
Slope = -1/8
So, we have
y = -1/8(x - 2) + 6
y = -1/8x + 25/4
The smallest slope on the curveWe have
f'(x) = 3x² - 4
Set to 0
3x² - 4 = 0
Solve for x
x = √[4/3]
x = 1.15
So, we have
Smallest slope = (√[4/3])³ - 4(√[4/3]) + 6
Smallest slope = 2.92
So, the smallest slope is 2.92 at (1.15, 2.92)
The equation of the tangent lineHere, we set f'(x) to 8
3x² - 4 = 8
Solve for x
x = ±2
Calculate y at x = ±2
y = (-2)³ - 4(-2) + 6 = 6: (-2, 0)
y = (2)³ - 4(2) + 6 = 6: (2, 0)
The equations at these points are
y = 8x + 16
y = 8x - 16
Read more about tangent lines at
https://brainly.com/question/21595470
#SPJ1
please help.
definitions: 1. definition of right triangle
2. definition of isosceles TrianglesReflexive
3. HL
4. definition of perpendicular
5. CPCTC
6. reflexive

Answers
From the two column proof below, we have seen ∠BAC ≅ ∠DAC by CPCTC
How to solve two column proof problems?The two column proof to show that ∠BAC ≅ ∠DAC is as follows:
Statement 1: ΔABD is Isosceles with base BD, AC ⊥ BD
Reason 1: Given
Statement 2: AB ≅ AD
Reason 2: Definition of isosceles Triangles
Statement 3: ∠1 and ∠2 are right angles
Reason 3: Definition of perpendicular
Statement 4: AC ≅ AC
Reason 4: Reflexive Property
Statement 5: ΔABC and ΔADC are right triangles
Reason 5: Definition of right triangle
Statement 6: ΔABC ≅ ΔADC
Reason 6: HL Congruency
Statement 7: ∠BAC ≅ ∠DAC
Reason 7: CPCTC
Read more about two column proof at; brainly.com/question/1788884
#SPJ1
how much money deposited now will provide payment of Rs. 15000 at the end of each half year for 10 years, if interest is 16% compounded six-monthly
Answers
The interest is 16% compounded semi-annually, is Rs. 121,179.10.
To determine how much money needs to be deposited now to provide a payment of Rs. 15,000 at the end of each half year for 10 years, we will use the formula for the present value of an annuity.
Present value of an annuity = (Payment amount x (1 - (1 + r)^-n))/rWhere:r = interest rate per compounding periodn = number of compounding periodsPayment amount = Rs. 15,000n = 10 x 2 = 20 (since there are 2 half years in a year and the payments are made for 10 years)
So, we have:r = 16%/2 = 8% (since the interest is compounded semi-annually)Payment amount = Rs. 15,000Using the above formula, we can calculate the present value of the annuity as follows:
Present value of annuity = (15000 x (1 - (1 + 0.08)^-20))/0.08 = Rs. 121,179.10Therefore, the amount that needs to be deposited now to provide payment of Rs. 15,000 at the end of each half year for 10 years, if the interest is 16% compounded semi-annually, is Rs. 121,179.10.
For more such questions on semi-annually
https://brainly.com/question/30573341
#SPJ8
A die is rolled. If it rolls to a 1, 2, or 3 you win $2. If it rolls to a 4, 5, or 6 you lose $1. Find the expected winnings.
a) $0.50
b) $3.00
c) $1.50
d) $1.00
Answers
Answer:
A. $0.5
Step-by-step explanation:
In this question half of the time your winning is 2 dollars and also the other half of the time your loss is one dollar
The expectation is that after you must have had 2 rolls you would get 2 dollars once and also you are going to lose 1 dollar once. So what you won overall would be 1 dollar.
So the correct answer would be gotten from $1/2rolls
= $0.50
For every 9 pages I read I took 1.5 pages of notes, if I read 28 pages, how many pages of notes will I have taken?
Answers
Answer:
168 pages of notes
Step-by-step explanation:
9 divided by 1.5= 6
so 28x6= 168
In the game of roulette, a player can place a $6 bet on the number 10 and have a 1/38 probability of winning. If the metal ball lands on 10, the player gets to keep the $6 paid to play the game and the player is awarded an additional $210. Otherwise, the player is awarded nothing and the casino takes the player's $6.
(a) What is the expected value of the game to the player? (Round to the nearest cent as needed.)
(b) If you played the game 1000 times, how much would you expect to lose?
Note that the expected value is the amount, on average, one would expect to gain or lose each game. (Round to the nearest cent as needed.)
Answers
The expected value of the game to the player is $5.95, and if they play 1000 times, they would expect to lose $5950.
The expected value of the game to the player is the average amount of money they can expect to win or lose in the long run. To calculate the expected value, we must multiply the probability of winning (1/38) by the amount of money won ($210) and subtract the probability of losing (37/38) by the amount of money paid to play ($6). This gives us an expected value of (1/38) x ($210) - (37/38) x ($6) = $5.95. If you played the game 1000 times, you would expect to lose $5950 in total, as the expected value of each game is -$5.95. This means that, on average, you would lose $5.95 for every game you play. Multiplying this amount by 1000 gives us our expected total loss of $5950.
The calculation for the expected value of the game and the total expected loss for playing it 1000 times is as follows:
Expected value = (1/38) x ($210) - (37/38) x ($6)
= ($5.526) - ($5.684)
= -$0.158
Therefore, the expected value of each game is -$0.158, which means that on average, a player can expect to lose $0.158 for every game played.
Total expected loss for playing 1000 times = (-$0.158) x 1000
= -$158
Therefore, if the game is played 1000 times, the total expected loss is -$158
Learn more about expected value here
https://brainly.com/question/18523098
#SPJ1
24, 12, 6
Find the 10th term for this geometric sequence
Answers
Answer:
0.0234375
Step-by-step explanation:
You just keep dividing by 2
If I'm wrong, sorry
Answer:
0.046875 aka 3/64
Step-by-step explanation:
In a geometric sequence, each term will be related to the previous term by undergoing either multiplication or division.
In this case, each case is exactly 1/2 of the previous term. 12 is half of 24, and 6 is half of 12. By continuing this sequence, we get
1: 24
2: 12 (24 * 1/2)
3: 6 (12 * 1/2)
4: 3 (6 * 1/2)
5: 3/2 (3 * 1/2)
6: 3/4 (3/2 * 1/2)
7. 3/8 (3/4 * 1/2)
8. 3/16 (3/8 * 1/2)
9. 3/32 (3/16 * 1/2)
10. 3/64 (3/32 * 1/2)
What is the M.A.D. (mean absolute deviation) of the following data set?
8 9 9 7 8 6 9 8
Answers
The mean absolute deviation is 0.75
How to determine the mean absolute deviationTo calculate the mean absolute deviation (M.A.D.), you need to find the average of the absolute differences between each data point and the mean of the data set
From the information given, we have that the data set is;
8 9 9 7 8 6 9 8
Let's calculate the mean, we get;
Mean = (8 + 9 + 9 + 7 + 8 + 6 + 9 + 8) / 8
Mean = 64 / 8
Divide the values
Mean = 8
Let's determine the absolute difference, we get;
Absolute differences=
|8 - 8| = 0
|9 - 8| = 1
|9 - 8| = 1
|7 - 8| = 1
|8 - 8| = 0
|6 - 8| = 2
|9 - 8| = 1
|8 - 8| = 0
Find the mean of the absolute differences:
Average of absolute differences = (0 + 1 + 1 + 1 + 0 + 2 + 1 + 0) / 8
Absolute difference = 6 / 8 = 0.75
Learn more about mean absolute deviation at: https://brainly.com/question/447169
#SPJ1
Is the product of 15 and
2/3 more or less than 15? Explain your answer in complete sentences.
Answers
Answer:
its less than 15. your basically getting 2/3 out of 15.
Step-by-step explanation:
15x2= 30
=30/3= 10
10 is less than 15
Hope this helps and please brainliest
at what values of x does fx0
Answers
Values of x is -2, 1 and 3 for which f(x) = 0.
Option (b) , (d) and (e) are correct.
Information available from the question:
The complete question is this:
At what values of x, does f(x)=0? mark all that apply
a.-4
b.-2
c.0
d.1
e.3
f.8
Now, According to the question:
x-intercepts is the value of x for which f(x) = 0 i.e, where the graph of the function crosses the x-axis and is found by solving the equation f(x) = 0.
we have to find the values of x where f(x) =0
From the given graph you can see that the graph crosses the x-axis at three points (x, f(x))
i.e., (-2 ,0) , (1, 0) and (3, 0)
Therefore, the values of x for which f(x) = 0 is, -2 , 1 and 3
Learn more about Graph at:
https://brainly.com/question/10712002
#SPJ4

Solve the system of equations using the substitution or elimination method.
y = 4x - 7
4x + 2y = -2
.
Show your work
Correct x and y
Answers
The solution to the system of equations is x = 1 and y = -3.
To solve the system of equations using the substitution or elimination method, let's start with the substitution method.
Given equations:
y = 4x - 7
4x + 2y = -2
We'll solve equation 1) for y and substitute it into equation 2):
Substituting y from equation 1) into equation 2):
4x + 2(4x - 7) = -2
4x + 8x - 14 = -2
12x - 14 = -2
Now, we'll solve this equation for x:
12x = -2 + 14
12x = 12
x = 12/12
x = 1
Now that we have the value of x, we can substitute it back into equation 1) to find y:
y = 4(1) - 7
y = 4 - 7
y = -3
Therefore, the solution to the system of equations is x = 1 and y = -3.
for such more question on system of equations
https://brainly.com/question/4262258
#SPJ8
Can I please get some help I’ve been stuck on this question for a while!

Answers
Using the radius of the Ferris wheel and the angle between the two positions, the time spent on the ride when they're 28 meters above the ground is 12 minutes
How many minutes of the ride are spent higher than 28 meters above the ground?The radius of the Ferris wheel is 30 / 2 = 15 meters.
The highest point on the Ferris wheel is 15 + 4 = 19 meters above the ground.
The time spent higher than 28 meters is the time spent between the 12 o'clock and 8 o'clock positions.
The angle between these two positions is 180 degrees.
The time spent at each position is 10 minutes / 360 degrees * 180 degrees = 6 minutes.
Therefore, the total time spent higher than 28 meters is 6 minutes * 2 = 12 minutes.
Learn more on a Ferris wheel here;
https://brainly.com/question/30524034
#SPJ1
The graph below shows the value of Edna's profits f(t), in dollars, after t months: graph of quadratic function f of t having x intercepts at 6, 0 and 18, 0, vertex at 12, negative 36, and passes through point 21, 41.25 What is the closest approximate average rate of change for Edna's profits from the 18th month to the 21st month?
Answers
The closest approximate average rate of change for Edna's profits from the 18th month to the 21st month is 14
How to determine the average rate of change?From the question, we have the following ordered pairs
x intercepts = (6,0) and (18, 0)
Vertex = (12, -36)
Points (21, 41.25)
The closest approximate average rate of change for Edna's profits from the 18th month to the 21st month is the calculated using
m = [f(21) - f(18)]/[21 - 18]
This becomes
m = [f(21) - f(18)]/3
Substitute the known values in the above equation
m = [41.25 - 0]/3
Evaluate the difference
m = 41.25/3
Evaluate the quotient
m = 13.75
Approximate
m=14
Hence, the closest approximate average rate of change for Edna's profits from the 18th month to the 21st month is 14
Read more about average rate of change at
https://brainly.com/question/8728504
#SPJ1
Complete question
The graph below shows the value of Edna's profits f(t), in dollars, after t months:
What is the closest approximate average rate of change for Edna's profits from the 18th month to the 21st month?
See attachment for graph

Find the first five terms of the sequence defined below:

Answers
Answer:
d. 7, -14, 28, -56, 112
Step-by-step explanation:
f(2) = -2(7) = -14
f(3) = -2(-14) = 28
f(4) = -2(28) = -56
f(5) = -2(-56) = 112
on a coordinate plane which quadrant is shaded\(y\leq x\)
Answers
We can see that the first and third quadrants are half-shaded, and the fourth quadrant is totally shaded.
Which quadrants are shaded?Here we have the following inequality:
y ≤ x
The shaded region would be the solution set of that inequality, to get that we need to graph the line:
y = x
Which divides the coordinate plane, and then shade the region below that line (because y is smaller than or equal to x)
Then the graph you will get is like the one below.
There you can see that the first and third quadrans are half shaded, and the fourth quadrant is totally shaded.
Learn more about inequalities:
https://brainly.com/question/24372553
#SPJ1
![on a coordinate plane which quadrant is shaded[tex]y\leq x[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/dy9YX7nlWDMvxbR8goMDCEo4HrTgJRCk.png)
Mr. Gupta gave his students a quiz with three questions on it. Let
�
XX represent the number of questions that a randomly chosen student answered correctly. Here is the probability distribution of
�
XX along with summary statistics:
�
=
# correct
X=# correctX, equals, start text, \#, space, c, o, r, r, e, c, t, end text
0
00
1
11
2
22
3
33
�
(
�
)
P(X)P, left parenthesis, X, right parenthesis
0.05
0.050, point, 05
0.20
0.200, point, 20
0.50
0.500, point, 50
0.25
0.250, point, 25
Mean:
�
�
=
1.95
μ
X
=1.95mu, start subscript, X, end subscript, equals, 1, point, 95
Standard deviation:
�
�
≈
0.8
σ
X
≈0.8sigma, start subscript, X, end subscript, approximately equals, 0, point, 8
Mr. Gupta decides to score the tests by giving
10
1010 points for each correct question. He also plans to give every student
5
55 additional bonus points. Let
�
YY represent a random student's score.
What are the mean and standard deviation of
�
YY?
Answers
The mean score of a random student (YY) is 574.5. the standard deviation of the random student's score (YY) is 8.
How to answer the aforementioned questionGiven:
- Each correct question is worth 10 points.
- Every student receives an additional 555 bonus points.
Let's calculate the mean and standard deviation of YY:
Mean of YY:
The mean score, denoted as μY, can be calculated using the mean of XX (μX) and the scoring scheme:
μY = μX * 10 + 555
Substituting the value of μX from the given information:
μY = 1.95 * 10 + 555
μY = 19.5 + 555
μY = 574.5
Therefore, the mean score of a random student (YY) is 574.5.
Standard Deviation of YY:
The standard deviation of YY, denoted as σY, can be calculated using the standard deviation of XX (σX) and the scoring scheme:
σY = σX * 10
Substituting the value of σX from the given information:
σY = 0.8 * 10
σY = 8
Therefore, the standard deviation of the random student's score (YY) is 8.
Complete question: Mr. Gupta gave his students a quiz with three questions on it. Let X represent the number of questions
that a randomly chosen student answered correctly. Here is the probability distribution of X along with
summary statistics:
0
1
2
2.
3
X = # correct
P(X)
0.05
0.20
0.50
0.25
Mean: Hex = 1.95
Standard deviation: Ox 0.8
Mr. Gupta decides to score the tests by giving 10 points for each correct question. He also plans to give
every student 5 additional bonus points. Let Y represent a random student's score.
What are the mean and standard deviation of Y?
Learn more about standard deviation at https://brainly.com/question/475676
#SPJ1
Consider the chart of LCD Television sets and population below. Round your ratio as a decimal to 6 places. Round the Owners per 100 to one decimal.
City
Number of Owners
Total Population
Ratio as decimal
Owners per 100
Indianapolis
6,245
0.90 million
New York
911,216
18.6 million
Cairo
10,598
19.1 million
Beijing
959,611
21.2 million
Tokyo
1,700,510
26.5 million
Answers
To calculate the ratio as a decimal, we divide the number of owners by the total population for each city.
For Indianapolis: Ratio = 6,245 / 0.9 million = 0.006938
For New York: Ratio = 911,216 / 18.6 million = 0.049019
For Cairo: Ratio = 10,598 / 19.1 million = 0.000554
For Beijing: Ratio = 959,611 / 21.2 million = 0.045270
For Tokyo: Ratio = 1,700,510 / 26.5 million = 0.064234
To calculate the owners per 100, we multiply the ratio by 100.
For Indianapolis: Owners per 100 = 0.006938 * 100 = 0.7 (rounded to one decimal place)
For New York: Owners per 100 = 0.049019 * 100 = 4.9 (rounded to one decimal place)
For Cairo: Owners per 100 = 0.000554 * 100 = 0.1 (rounded to one decimal place)
For Beijing: Owners per 100 = 0.045270 * 100 = 4.5 (rounded to one decimal place)
For Tokyo: Owners per 100 = 0.064234 * 100 = 6.4 (rounded to one decimal place)
Therefore, the ratio as a decimal and the owners per 100 for each city are as follows:
Indianapolis: Ratio = 0.006938, Owners per 100 = 0.7
New York: Ratio = 0.049019, Owners per 100 = 4.9
Cairo: Ratio = 0.000554, Owners per 100 = 0.1
Beijing: Ratio = 0.045270, Owners per 100 = 4.5
Tokyo: Ratio = 0.064234, Owners per 100 = 6.4
For such more question on Ratio
https://brainly.com/question/12024093
#SPJ8
(Irrational Numbers MC)
Approximate -10 + √30 to the nearest tenth. HELP PLS
Answers
-10 + 5.47722~
=4.523~
round to nearest tenth = 4.5
Answer:
-4.5
Step-by-step explanation:
\(\sqrt{30}\) is approximately 5.47722557505. You can find this number with a calculator.
-10 + 5.47722557505 = -4.52277442495
To add a negative and a positive number, you subtract the absolute values and take the sign of the number that has the larger absolute value. Absolute value just means thinking of both numbers as positive numbers.
Helping in the name of Jesus.
3. Study Hours (Based on Exercise 8.7) Babcock and Marks (2010) reviewed survey data from 2003–2005 and obtained an average of µ = 14 hours per week spent studying by full-time students at 4-year colleges in the United States. To determine whether this average changed over the 10 subsequent years, a researcher selected a sample of = 64 of college students. The data file hours.csv has data consistent with what the researcher found. In this question, you will use the data to if this sample indicates a significant change in the number of hours spent studying.
a. Which of the following are the hypotheses to test if this sample indicates a significant change in the average number of hours spent studying?
i. 0: µ = 14 and 1: µ < 14
ii. 0: µ = 14 and 1: µ ≠ 14
iii. 0: µ = 14 and 1: µ > 14
Answers
The hypotheses to test if this sample indicates a significant change in the average number of hours spent studying is:
0: µ = 14 (null hypothesis)
1: µ ≠ 14 (alternative hypothesis)
Option B is the correct answer.
We have,
The null hypothesis states that the population mean for the number of hours spent studying by full-time students at 4-year colleges in the United States is equal to 14 hours per week,
while the alternative hypothesis states that it is different from 14 hours per week.
By using a two-tailed test, we are checking for any significant change in either direction, whether the average number of hours spent studying has increased or decreased from 14 hours per week.
Thus,
The hypotheses to test if this sample indicates a significant change in the average number of hours spent studying is:
0: µ = 14 (null hypothesis)
1: µ ≠ 14 (alternative hypothesis)
Learn more about hypothesis testing here:
https://brainly.com/question/30588452
#SPJ1
What is the constant up a proportionally in a equation y=x/g
Answers
Answer:
Step-by-step explanation:
\(y=(\frac{1}{g} )x\)
Constant up a proportionally is \(\frac{1}{g}\).
Please answer this correctly

Answers
Answer:
The area of the quarter circle = 346.19 miles²
Step-by-step explanation:
If the perimeter of a quarter circle = 74.97 miles
r + r + 1/4 * 2pi*r = 74.97 miles
2r + 1/2r * pi = 74.97
Multiply left and right of the = sign by 2 gives...
2 * ( 2r + 1/2 * r * pi ) = 74.97 * 2
( 4r + 2/2* r * pi ) = 149.94
r * ( 4 + 3.14 ) = 149.94
r * ( 7.14 ) = 149.94
7.14 * r = 149.94
Divide left and right of the equal sign by 7.14
7.14 / 7.14 * r = 149.94 / 7.14
r = 149.94 / 7.14
r = 21 miles
Area full circle = r² * pi
21² * pi
441 * pi
We need to calculate a quarter part of the area of the full circle, so
1/4 * 441 * pi
110.25 * pi
110.25 * 3.14
= 346.185, which rounded to the hundreth gives.
The area of the quarter circle = 346.19 miles²
Answer: 346.19 miles²
Step-by-step explanation:
Perimeter (P) of the quarter circle is the curve + both sides.
Perimeter of the curve
\(\dfrac{1}{4}C=\dfrac{1}{4}2\pi\cdot r\\\\\\.\quad =\dfrac{\pi \cdot r}{2}\)
Perimeter of the sides
2 sides = 2r
Perimeter = curve + both sides
\(74.97=\dfrac{\pi \cdot r}{2}+2r\\\\\\2(74.97)=\pi \cdot r+2(2r)\\\\\\149.94=\pi r+4r\\\\\\149.94=r(\pi +4)\\\\\\\dfrac{149.94}{\pi +4}=r\\\)
Find the Area
\(\dfrac{1}{4}A=\dfrac{1}{4}\pi\bigg(\dfrac{149.94}{\pi+4}\bigg)^2\\\\\\.\quad =\dfrac{1}{4}3.14\bigg(\dfrac{149.94}{3.14+4}\bigg)^2\\\\\\.\quad =\dfrac{1}{4}3.14(21)^2\\\\\\.\quad =\large\boxed{346.185}\)
A population of 1,000 students spends an average of $10.50 a day on dinner. The standard deviation of the expenditure is $3. A simple random sample of 64 students is taken. a. What are the expected value, standard deviation, and shape of the sampling distribution of the sample mean
Answers
Answer:
expected value is the mean : 10.5
Standard error for the sampling distribution : 0.375
it has a bell-shaped curve with 99.7% of the values between 9.375 and 11.625
Step-by-step explanation:
In an orchard 2/5 of the trees are banana trees, 1/4 of the trees are orange trees and the rest are apple trees. If there are 220 trees in all, find the number of each kind
Answers
Answer: banana- 88
Orange-55
Apple-143
Step-by-step explanation:
220 divided by 5, times 2,
that’s the banana trees
220 divided by 4, that’s the oranges
Add the answers together
Take the answer away from 220 that’s the apples
2tan(x/2)- csc x=0 interval [0,2pi)
Answers
Answer:
\(x= \dfrac{\pi}{3}, \;\;x=\dfrac{5 \pi}{3}\)
Step-by-step explanation:
Given trigonometric equation:
\(2 \tan\left(\dfrac{x}{2}\right)- \csc x=0\)
To solve the equation for x in the given interval [0, 2π), first rewrite the equation in terms of sin x and cos x using the following trigonometric identities:
\(\boxed{\begin{minipage}{4cm}\underline{Trigonometric identities}\\\\$\tan \left(\dfrac{\theta}{2}\right)=\dfrac{1-\cos \theta}{\sin \theta}$\\\\\\$\csc \theta = \dfrac{1}{\sin \theta}$\\ \end{minipage}}\)
Therefore:
\(2 \tan\left(\dfrac{x}{2}\right)- \csc x=0\)
\(\implies 2 \left(\dfrac{1-\cos x}{\sin x}\right)- \dfrac{1}{\sin x}=0\)
\(\implies \dfrac{2(1-\cos x)}{\sin x}- \dfrac{1}{\sin x}=0\)
\(\textsf{Apply the fraction rule:\;\;$\dfrac{a}{c}-\dfrac{b}{c}=\dfrac{a-b}{c}$}\)
\(\dfrac{2(1-\cos x)-1}{\sin x}=0\)
Simplify the numerator:
\(\dfrac{1-2\cos x}{\sin x}=0\)
Multiply both sides of the equation by sin x:
\(1-2 \cos x=0\)
Add 2 cos x to both sides of the equation:
\(1=2\cos x\)
Divide both sides of the equation by 2:
\(\cos x=\dfrac{1}{2}\)
Now solve for x.
From inspection of the attached unit circle, we can see that the values of x for which cos x = 1/2 are π/3 and 5π/3. As the cosine function is a periodic function with a period of 2π:
\(x=\dfrac{\pi}{3} +2n\pi,\; x=\dfrac{5\pi}{3} +2n\pi \qquad \textsf{(where $n$ is an integer)}\)
Therefore, the values of x in the given interval [0, 2π), are:
\(\boxed{x= \dfrac{\pi}{3}, \;\;x=\dfrac{5 \pi}{3}}\)

Please set up the equation in y=__x+__ form please