The length between the bases on a baseball field is 90 feet. A scale drawing shows the distance between the bases are 2 1/5 inches. one inch on this drawing equals how many feet?
Answers
Answer:
So the distance from home plate to 2nd base is 127.279 ft
Step-by-step explanation:
I think it is right hope it helps :)
Answer:
Step-by-step explanation:
Jordan created a scale drawing of a rectangular room. The drawing is 8 inches long by 6 inches wide He used a scale of 2 inch = 3 feet . What id the area ,in square feet , of the room
Related Questions
evaluate 3d/2a, when d=4 and a = -1
Answers
Answer:
ok
Step-by-step explanation:
Please Help WILL MARK BRANLIEST

Answers
Answer:
n = 7
Step-by-step explanation:
You have a geometric sequence with first term 625 and common ratio 1/5, and you want to know the number of the term whose value is 1/25.
Geometric sequenceThe general term of a geometric sequence is ...
tn = t1·r^(n-1)
Using the given values, we can solve for n:
1/25 = 625·(1/5)^(n-1)
1/(5^2·5^4) = 1/5^(n-1) . . . . . . divide by 625; write as powers of 5
Comparing exponents of 5, we have ...
6 = n -1
7 = n
The value of n for which tn = 1/25 is 7.
__
Additional comment
The attachment shows the first 7 terms of the sequence.
<96141404393>

Help!! Thank you so much!!
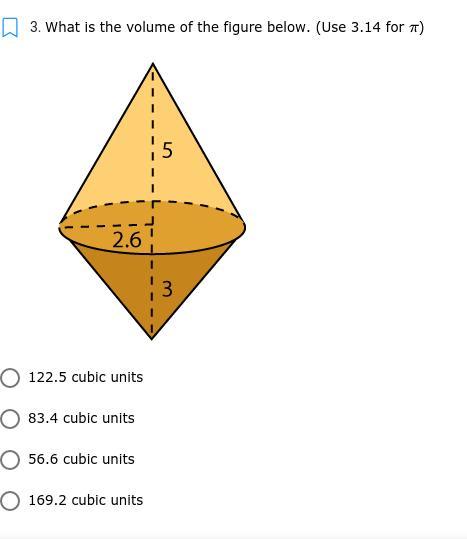
Answers
The volume we're looking for is the volume of both cones in the figure.
The volume of a cone is \(V=\pi r^2\frac{h}{3}\) .
So, \(V_{tot} = V_{1} + V_2\) .
Cone 1's variables:
r = 2.6
h = 5
Cone 2's variables:
r = 2.6
h = 3
Now we can just plug and chug!
\(V_{tot} = [(3.14)(2.6^2)(\frac{5}{3} )] + [(3.14)(2.6^2)\frac{3}{3} )]\\V_{tot} = [(3.14)(6.76)(1.67)] + [(3.14)(6.76)(1)]\\V_{tot} = (35.45) + (21.23)\\V_{tot} = 56.68\)
V = c. 56.6 cubic units
Use place value to explain each step in finding
3 x 2,746
Answers
The value of the given expression 3 x 2,746 is 8,238.
We are given the expression:-
3 x 2,746
We have to find the value of the given expression using place value.
According to the data given in the question, we can write,
In 2746,
The place value of 6 is 6
The place value of 4 is 4*10 = 40
The place value of 7 is 7*100 = 700
The place value of 2 is 2*1000 = 2000
Hence, we can write,
3*2746 = 3*2000 + 3*700 + 3*40 + 3*6 = 6000 + 2100 + 120 + 18 = 8,238.
To learn more about place value, here:-
https://brainly.com/question/27734142
#SPJ1
Find the sum of the first 7 terms of the following series, to the nearest integer. 125,50,20,...
Answers
Answer:208
Step-by-step explanation:
Application Normal Distribution (finding the probability and scores)
The weights of adults living in the town of Metaluna is normally distributed, with a mean of 146 pounds and a standard deviation of 12.7 pounds. Given this information, please compute the following:
(Show all work – Formula and calculations)
The probability that an adult sampled at random will weigh between 136 pounds and 164 pounds. Please show illustration
Answers
The probability that an adult sampled at random will weigh between 136 pounds and 164 pounds can be calculated using the properties of the normal distribution.
To find the probability, we need to calculate the area under the normal curve between the two weight values. We can convert the given weights into z-scores (standardized scores) using the formula:
z = (x - μ) / σ
where x is the given weight, μ is the mean weight, and σ is the standard deviation.
For the lower weight value of 136 pounds:
z1 = (136 - 146) / 12.7 = -0.79
For the upper weight value of 164 pounds:
z2 = (164 - 146) / 12.7 = 1.42
Now, we can look up the corresponding z-scores in the standard normal distribution table or use a calculator to find the area under the curve between these z-scores. The probability is equal to the difference between these two areas.
Using a standard normal distribution table or calculator, we find the area to the left of z1 (0.2139) and the area to the left of z2 (0.9236). Therefore, the probability of an adult weighing between 136 and 164 pounds is:
P(136 < x < 164) = P(-0.79 < z < 1.42) = P(z < 1.42) - P(z < -0.79) = 0.9236 - 0.2139 = 0.7097
The probability that an adult sampled at random will weigh between 136 and 164 pounds is approximately 0.7097 or 70.97%. This means that there is a 70.97% chance of randomly selecting an adult whose weight falls within this range in the town of Metaluna, assuming the weights follow a normal distribution with a mean of 146 pounds and a standard deviation of 12.7 pounds.
Learn more about probability here:
brainly.com/question/31828911
#SPJ11
18. If f(x) = arccos(x^2), then f'(x) =
Answers
The derivative of f(x) = arccos(x^2) is: f'(x) = -2x / √(1-x^4)
The derivative of f(x) = arccos(x^2), we'll use the chain rule. The chain rule states that the derivative of a composite function is the derivative of the outer function times the derivative of the inner function. In this case, the outer function is arccos(u) and the inner function is u = x^2.
First, let's find the derivative of the outer function, arccos(u). The derivative of arccos(u) is -1/√(1-u^2). Next, we'll find the derivative of the inner function, x^2. The derivative of x^2 is 2x.
Now we'll apply the chain rule. We have:
f'(x) = (derivative of outer function) * (derivative of inner function)
f'(x) = (-1/√(1-u^2)) * (2x)
Since u = x^2, we'll substitute that back into our equation:
f'(x) = (-1/√(1-x^4)) * (2x)
So, the derivative of f(x) = arccos(x^2) is:
f'(x) = -2x / √(1-x^4)
To learn more about Derivative :
https://brainly.com/question/23819325
#SPJ11
The Jayden family eats at a restaurant that is having a 15% discount promotion. Their meal costs $78.82 before the discount, and they leave a 20% tip. If the tip applies to the cost of the meal before the discount, what is the total cost of the meal? Round your intermediate calculations and answer to the nearest cent.
Answers
Answer:
they would have to pay $80.22
40 POINTS!!!
Find the volume of this irregular figure.
Hint: Find the volume of the whole rectangular prism, then subtract the volume of the missing piece, which is also a rectangular prism.

Answers
Answer:
470 cm³
Step-by-step explanation:
Volume of rectangular prism = width × length × height
⇒ Volume of whole rectangular prism = 9 cm × 10 cm × 8 cm
= 720 cm³
Side lengths of the missing piece:
width = 5 cmlength = 10 cmheight = 8 cm - 3 cm = 5 cm⇒ Volume of the missing piece = 5 cm × 10 cm × 5 cm
= 250 cm³
⇒ Volume of irregular figure = 720 cm³ - 250 cm³
= 470 cm³
Find measure of angle PRS=98 degrees. Find measure of angle QRS. PRG= (3x-8) QRS= (2x+6)
Answers
The measure of angle QRS is 46 degrees.
First, let us understand the like terms;
Like terms in algebra are terms that have the same variables and powers. The coefficients do not have to be the same.
We are given;
Angle PRS = 98 degrees
Angle PRQ = (3x - 8) degrees
Angle QRS = (2x + 6) degrees
Also, the sum of angle PRQ and angle QRS is 98 degrees.
So,
(2x + 6) + (3x - 8) = 98 degrees
Combine like terms.
5x - 2 = 98 degrees
5x = 100 degrees
x = 20 degrees
Put the value of the x into the expressions for the given angle measures.
Angle QRS = 2x + 6 = 2(20) + 6 = 46 degrees
Angle PRQ = 3x - 8 = 3(20) - 8 = 52 degrees
Thus, the measure of angle QRS is 46 degrees.
To learn more about like terms visit:
https://brainly.com/question/23325290
#SPJ9
The following table shows the salary of 7 people in an office last year. Name Income Andy £9500 Bevan £30000 Cheryl £11250 Deva £72000 Elliott £12750 Frankie £29500 Grace £11000 a) Work out the mean income to 2 DP. b) Deva was given a large bonus for 30 years service. Excluding Deva's income, what was the mean income for the remaining 6 workers to 2 DP?
Answers
a) The mean income to 2 DP is £23714.28. b. If Deva's income is excluded, then the mean income will be £16,500.
What is addition?The addition is one of the mathematical operations. The addition of two numbers results in the total amount of the combined value.
a.
Andy = £9500
Bevan = £25000
Cheryl = £11250
Elliott = £12750
Frankie = £29500
Grace = £11000
Deva = £72000
Total Income = £166,000
To get the mean Income, we will divide the total income by 6 which is the number of people.
= £166,000/7
= £23714.28
b. If Deva's income is excluded, there'll be 6 people left.
Total income = £99000
Mean income = £99,000/6
= £16,500
a) The mean income to 2 DP is £23714.28. b. If Deva's income is excluded, then the mean income will be £16,500.
Learn more about addition here;
https://brainly.com/question/16972068
#SPJ1
A Rhombus has all its internal angles equal. If one of the diagonals is 15cm ,
find the length of the the other diagonal and the area of the Rhombus?
Answers
The area of the rhombus is approximately 112.5 square centimeters.
In a rhombus, all internal angles are equal, so we know that the opposite angles are congruent.
Additionally, the diagonals of a rhombus bisect each other at right angles, forming four congruent right triangles.
Let's denote the length of one diagonal as 15 cm, and the lengths of the sides of the rhombus as a.
Using the Pythagorean theorem, we can find the length of the other diagonal.
Let's label it as d.
In each right triangle, the hypotenuse is the length of a side, which is a, and one leg is half the length of the diagonal, which is 15/2 = 7.5 cm.
Applying the Pythagorean theorem, we have:
a² = (7.5)² + (7.5)²
a² = 56.25 + 56.25
a² = 112.5
a = √112.5
a ≈ 10.61 cm
Thus, the length of each side of the rhombus is approximately 10.61 cm.
Since the diagonals of a rhombus are perpendicular bisectors of each other, the other diagonal (d) is equal to the square root of the sum of the squares of the two sides.
Hence:
d² = a² + a²
d² = 2a²
d = √(2a²)
d = √(2 \(\times\) 10.61²)
d ≈ √(2 \(\times\) 112.5)
d ≈ √225
d ≈ 15 cm
So, the length of the other diagonal is approximately 15 cm.
To find the area of the rhombus, we can use the formula:
Area = (diagonal₁ \(\times\) diagonal₂) / 2
Substituting the values, we get:
Area = (15 \(\times\) 15) / 2
Area = 225 / 2
Area = 112.5 cm²
For similar question on rhombus.
https://brainly.com/question/20627264
#SPJ11
Find the slope of the line between the points (4, 10) and (-6, 10)
Answers
Determine the number of significant figures for the following: 0.098200 has significant figure(s). 1.68×10
4
has significant figures(s). 78,000,120 has significant figure(s). 1.008 has significant figure(s).
Answers
The number of significant figures for each given value is as follows: 0.098200 has 5 significant figures, 1.68×10^4 has 3 significant figures, 78,000,120 has 9 significant figures, and 1.008 has 4 significant figures.
Significant figures represent the precision and accuracy of a number. They include all the digits that carry meaning in a measurement or calculation. In the case of 0.098200, all the digits are non-zero and are considered significant. Therefore, it has 5 significant figures.
For 1.68×10^4, the number is written in scientific notation. The digits before the multiplication sign represent the significand, which in this case is 1.68. The exponent of 10 indicates the number of places the decimal point is moved to obtain the actual value. In this case, it is 4, which means the decimal point is moved four places to the right. The significand, 1.68, has three significant figures, and the exponent of 10 does not affect the significant figures. Therefore, the value has 3 significant figures.
In 78,000,120, the zeros are considered significant because they are between nonzero digits. Hence, all the digits contribute to the significant figures, resulting in 9 significant figures.
Lastly, for 1.008, the trailing zero after the decimal point is significant, as it indicates precision. Therefore, it has 4 significant figures.
In summary, the number of significant figures for each given value is 0.098200 with 5 significant figures, 1.68×10^4 with 3 significant figures, 78,000,120 with 9 significant figures, and 1.008 with 4 significant figures.
Learn more about Significant figures
brainly.com/question/29153641
#SPJ11
What number would correctly replace the G?

Answers
Answer:
40
Step-by-step explanation:
x is being multiplied by 8 to get y
so 5 x 8 = 40
Paula bought a ski jacket on sale for $8 less than half its original price. She paid $84 for the jacket. What was the original price?
Answers
The original price of the ski jacket is $184.
What is price?
The sum of money paid or the amount of compensation offered by one party to another in exchange for goods or services is known as a price. The cost of production can take on different names depending on the circumstance. If the item is a "good" in a commercial transaction, the cost of the item will probably be referred to as its "price".
Given:
Paula bought a ski jacket on sale for $8 less than half its original price.
She paid $84 for the jacket.
We have to find the original price of the ski jacket.
Let
The original price = x
The amount she bought it = x/2 - 8
She paid $84 for the jacket
Therefore,
84 = x/2 - 8
Add 8 on both sides,
84 + 8 = x/2 - 8 + 8
92 = x/2
x = 184
Hence, the original price of the ski jacket is $184.
To know more about price, click on the link
https://brainly.com/question/11938988
#SPJ1
#7 What is f(4) if f(1) = 3.2 and f(x + 1) = 2.5f(x)?
Answers
========================================================
Explanation:
We're given f(1) = 3.2 which says the first term of the sequence is 3.2
To find the second term, we use the other equation, which is the recursive equation. Plug in x = 1 to get...
f(x+1) = 2.5*f(x)
f(1+1) = 2.5*f(1)
f(2) = 2.5*f(1)
f(2) = 2.5*3.2
f(2) = 8
The second term is 8. We multiplied the previous term (3.2) by the factor 2.5 to get this second term.
The third term is handled pretty much in a similar fashion
third term = 2.5*(second term)
third term = 2.5*8
third term = 20
Lastly, the fourth term f(4) is...
f(x+1) = 2.5*f(x)
f(3+1) = 2.5*f(3)
f(4) = 2.5*f(3)
f(4) = 2.5*20
f(4) = 50
The fourth term is 50.
The first four terms are: 3.2, 8, 20, 50
problem solving an archeologist finds part of a circular plate. what was the diameter of the plate to the nearest tenth of an inch?a part of a circular plate is drawn. two chords of length 7 inches each are bisected perpendicularly by two segments passing through the center. the length of each segment is 6 inches.
Answers
The diameter of the circular plate is 16.3 inches (rounded to the nearest tenth of an inch).
The given figure can be visualized as a circle with two perpendicular chords of length 7 inches each.
The chords are bisected perpendicularly by two segments passing through the center, each of length 6 inches.
Now, we have to find the diameter of the circular plate.
To find the diameter, we have to draw a perpendicular line to the center from one of the endpoints of a chord.
This will give us a right triangle with one side as 3 inches (half of the length of the chord) and the hypotenuse as the radius of the circle.
Using Pythagoras theorem, we get:
r² = 3² + 6² = 45r = √45 = 3√5 inches
Since the radius is 3√5 inches, the diameter is 6√5 inches.
To get the value of the diameter to the nearest tenth of an inch, we substitute 3.16 for √5.
Therefore, the diameter of the circular plate is:
Diameter = 6(3.16) = 18.96 inches ≈ 16.3 inches (rounded to the nearest tenth of an inch).
Thus, the diameter of the circular plate is 16.3 inches (rounded to the nearest tenth of an inch).
for such more question on diameter
https://brainly.com/question/390660
#SPJ11
repost of this math question due in 5 minutes plzz helpp

Answers
it converges if the ratio is <1
so then we find the sum
we take the first term (200) and divide it by 1-0.8=0.2
200/0.2=1250 (B)
A market sells 6 cans of food for overy 7 boxes of food. The market sold a total of 26 cans and boxes today. How
many of each kind did the market soll?
A 6 cans and 20 boxes
B 12 cans and 14 boxes
C 14 cans and 12 boxes
D 20 cans and 6 boxes
Edge 2023
Answers
Answer:
B
Step-by-step explanation:
For every 7 boxes the market also sells 6 cans; therefore 13 cans and boxes are being sold.
If 26 cans and boxes were sold in total today, then 26/13 = 2
this means 2 of the 6 cans and 7 boxes;
2x6=12 cans
2x7=14 boxes
Therefore, the market sold 12 cans and 14 boxes today
Answer:
B. 12 cans and 14 boxes
Step-by-step explanation:
To calculate how many cans and boxes of food the market sold, set up and solve a system of equations.
Let "x" be the number of cans of food the market sold.
Let "y" be the number of boxes of food the market sold.
According to the given information, we know that the ratio of cans to boxes is 6 : 7. Therefore:
\(x :y=6:7\)
\(\dfrac{x}{y}=\dfrac{6}{7}\)
\(7x=6y\)
As the total number of cans and boxes sold is 26, this can be expressed as x + y = 26.
Therefore, the system of equations that models the given scenario is:
\(\begin{cases}7x=6y\\x + y = 26\end{cases}\)
To solve the system of equations, use the method of substitution.
Rearrange the second equation to isolate y:
\(y=26-x\)
Substitute this into the first equation to eliminate the term in y, and solve for x:
\(7x=6(26-x)\)
\(7x=156-6x\)
\(7x+6x=156-6x+6x\)
\(13x=156\)
\(13x \div 13=156 \div 13\)
\(x=12\)
Substitute the found value of x into the rearranged equation and solve for y:
\(y=26-12\)
\(y=14\)
Therefore, the market sold 12 cans and 14 boxes of food.
Learn more about systems of equations here:
https://brainly.com/question/28164947
find the exact value of the expression. cos π/16 cos 3π/16 - sin π/16 sin 3π/16
Answers
The exact value of the expression \(cos \pi /16\ cos 3\pi /16 - sin \pi /16\ sin 3\pi /16\ is\ (2 + \sqrt2)/4\).
How to simplify and evaluate expressions involving trigonometric functions?We can use the following trigonometric identity:
cos(a-b) = cos(a)cos(b) + sin(a)sin(b)
We have:
\(cos \pi /16\ cos 3\pi /16 - sin \pi /16\ sin 3\pi /16 \\= cos(3\pi /16 - \pi /16) \\= cos \pi /8\)
Now, using the half-angle identity \(cos(\theta/2) = ^+_-\sqrt{[(1 + cos \theta)/2]\), we can simplify cos π/8:
\(cos \pi /8 \\= cos(\pi /4 - \pi /8) \\= cos \pi /4\ cos \pi /8 + sin \pi /4\ sin \pi /8 \\= 1/\sqrt{2} \times \sqrt{[(1 + cos \pi /4)/2]} + 1/\sqrt{2} \times \sqrt{[(1 - cos \pi /4)/2]} \\= 1/\sqrt{2} \times \sqrt{[(1 + 1/\sqrt{2})/2]} + 1/\sqrt{2} \times \sqrt{[(1 - 1/\sqrt{2})/2] }\)
\(= 1/\sqrt{2} \times \sqrt{[(2 + \sqrt{2})/4] }+ 1/\sqrt{2} \times \sqrt{[(2 - \sqrt{2})/4]} \\= 1/2 \times \sqrt{(2 + \sqrt{2})} + 1/2 \times \sqrt{(2 - \sqrt{2})} \\= \sqrt{2}/2 + \sqrt{2}/2\sqrt{2} + \sqrt{2}/2 - \sqrt{2}/2\sqrt{2} \\= \sqrt{2}/2 + \sqrt{2}/4 \\= (2 + \sqrt{2})/4\)
Therefore, the exact value of the expression \(cos \pi /16\ cos 3\pi /16 - sin \pi /16\ sin 3\pi /16\ is\ (2 + \sqrt2)/4\).
Learn more about trigonometric identity
brainly.com/question/3785172
#SPJ11
Colin needs to make 18 dozen cookies for a bake sale. The recipe he plans to use makes 6 dozen cookies and requires cup of sugar. A 5-
pound bag of sugar holds 12 cups and costs $3.60. About how much will the sugar cost to make 18 dozen
Answers
Answer:
OK
Step-by-step explanation:
F=9/5C + 32 solve for C
Answers
To solve for C let us do these steps
1. Put the term of C on one side and the other terms on the other side
Subtract 32 from both sides to move the term 32 to the other side
\(\begin{gathered} F-32=\frac{9}{5}C+32-32 \\ F-32=\frac{9}{5}C \end{gathered}\)2. Make the coefficient of C = 1
Divide both sides by 9/5
\(\begin{gathered} \frac{F-32}{\frac{9}{5}}=\frac{\frac{9}{5}C}{\frac{9}{5}} \\ \frac{5}{9}(F-32)=C \\ C=\frac{5}{9}(F-32) \end{gathered}\)You can Multiply the bracket (F- 32) by 5/9
\(C=\frac{5}{9}F-\frac{160}{9}\)11. What is the center of the circle (x - 2)2 + (y + 6)2 = 25?
Answers
If you’re solving for y, it’s y= 17/2 - x
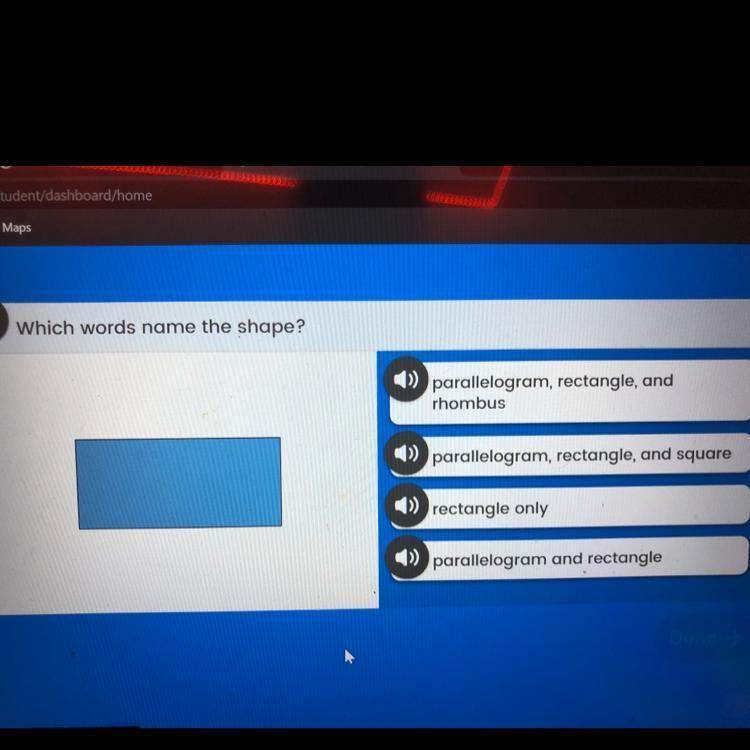
which words name the shape ?
Answers
Answer:
Parallelogram and rectangle
Step-by-step explanation:
Answer:
parallelogram and rectangle
Use the Distributive Property to find (5s+6)(s−2).
Answers
Answer:
5s^2 - 4s - 12
Step-by-step explanation:
Answer:
5s^2+4-12
Step-by-step explanation:
Find the Area of the figure below.

Answers
Answer:
Your answer is 9x^6*y^2π
Step-by-step explanation:
The formula for a circle is πr^2, with r as the radius.
Since 3x^3*y is the radius, you put that value in to get the equation:
(3x^3*y)^2*π
Once simplified, you get 9x^6*y^2π.
You can simplify further using the value of π, but it depends if the questions wants you to or not, mostly it doesn't.
I hope this was helpful.
There are 4 students at the Math Club picnic. If 2 students are drinking punch
and 2 are drinking lemonade, what fraction are drinking punch?
Simplify your answer as much as you can
Answers
Answer: 1/2
If 2 students are drinking punch
and 2 are drinking lemonade that would mean it would be 2/4
but if you were to simplify by dividing both by 2
it would be 1/2.
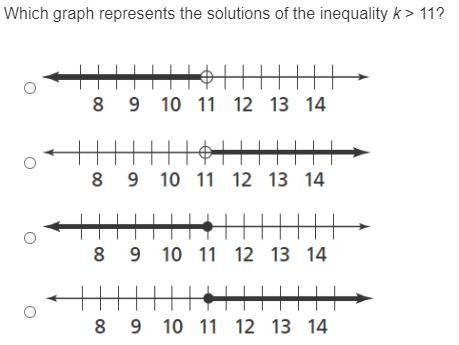
anyone can help me ?
Answers
Answer:
the 4th one
Step-by-step explanation:
it shows that k is greater than 11
I need a answer fast thanks!

Answers
Answer:
Chart:
x y
-6 11
3 5
15 -3
-12 15
Step-by-step explanation:
The only things you can plug in are the domain {-12, -6, 3, 15}
Plug in the domain into equation to find y.
-6 :
y = -2/3 (-6) +7
y = +47
y=11
(-6,11)
3:
y = -2/3 (3) +7
y = -2 +7
y = 5
(3, 5)
15:
y = -2/3 (15) +7
y = -10 +7
y = -3
(15 , -3)
-12:
y = -2/3 (-12) +7
y = 8 + 7
y= 15
(-12,15)
Answer:
1) 11
2) 3
3) -3
4) -12
Step-by-step explanation:
eq(1):
\(y = \frac{-2}{3} x + 7\\\\y - 7 = \frac{-2}{3} x\\\\x = (y - 7)\frac{-3}{2} \\\\x = (7-y)\frac{3}{2} ---eq(2)\)
1) x = -6
sub in eq(1)
\(y = \frac{-2}{3} (-6) + 7\\\\y = \frac{12}{3} + 7\\\\y = 4+7\\\\y = 11\)
2) y = 5
sub in eq(2)
\(x = (7-5)\frac{3}{2} \\\\x = 3\)
3) x = 15
sub in eq(1)
\(y = \frac{-2}{3} 15 + 7\\\\y = \frac{-30}{3} +7\\\\y = -10 + 7\\\\y = -3\)
4)
sub in eq(2)
\(x = (7-15)\frac{3}{2} \\\\x = -8\frac{3}{2}\\ \\x = -12\)