The heights of a certain population of corn plants follow a normal distribution with mean 145 cm and standard deviation 22 cm. Find the probability that none of the four plants will be more then 150cm tall.
Answers
The probability that none of the four plants will be more than 150 cm tall is approximately 0.4522.
What is the probability that all four plants are below 150 cm in height?To calculate the probability, we can use the concept of the standard normal distribution. By transforming the given data into a standard normal distribution, we can find the probability using a Z-table or a statistical calculator.
The first step is to standardize the value of 150 cm using the formula: Z = (X - μ) / σ, where X is the given value, μ is the mean, and σ is the standard deviation. Plugging in the values, we have Z = (150 - 145) / 22 = 0.2273.
Next, we find the cumulative probability corresponding to this Z-value. Looking up the Z-value in a standard normal distribution table or using a statistical calculator, we find that the cumulative probability is approximately 0.5903.
Since we want the probability that all four plants are below 150 cm, we multiply the individual probabilities together: 0.5903⁴ ≈ 0.09578.
However, we are interested in the probability that none of the four plants will be more than 150 cm tall. Therefore, we subtract the probability from 1: 1 - 0.09578 ≈ 0.9042.
So, the probability that none of the four plants will be more than 150 cm tall is approximately 0.9042, or 90.42%.
Learn more about probability
https://brainly.com/question/31828911
#SPJ11
Related Questions
If y=g(x), Find g(-3)= I've already tried 3, 4, 3.25, and 3

Answers
The function g(-3) has a value of 3.5
How to evaluate the function?From the question, we have the following parameters that can be used in our computation:
The graph of the function g(x)
Also, we have
y = g(x)
To calculate g(-3), we set x = -3
So, we have the following representation
y = g(-3)
Also from the graph
We have the following representation such that
When x = -3, the function is 3.5 (approximately)
So, we have the following representation
y = 3.5
Hence, the value of the function is 3.5
Read more about functions at
https://brainly.com/question/28532394
#SPJ1
What is the value of 24 + x ÷ 12 when x = −180?
Answers
Answer:
9
Step-by-step explanation:
1. Just input the x value with -180:
24 (+) -180 / 12 = answer
2. Follow PEMDAS to solve, which in this case division comes before addition:
24 + (-180 / 12)
24 + (-15)
3. Addition
24 + (-15) or 24 - 15
= 9
Therefore, 24 (+) -180 / 12 equals 9.
Molly placed $220. 00 in a savings account. This savings account earns 4. 2% interest per
year. She did not add or take out any money from this account. How much money did
she earn in interest at the end of six years?
Answers
Molly earned $282.37 - $220.00 = $62.37 in interest at the end of six years.
What is compound interest?
The interest on savings that is computed on both the initial principal and the interest accrued over time is known as compound interest. Compound interest is computed by multiplying the starting principal amount by one and the annual interest rate raised to the number of compound periods minus one. The final step is to deduct the initial loan principal from the calculated value.
To solve this problem, we can use the formula for compound interest:
\(A = P(1 + r/n)^(nt) \)
We are given that Molly placed $220.00 in a savings account with an annual interest rate of 4.2%. We are also told that she did not add or take out any money from the account, so the principal remains $220.00. Since we are not given how many times per year the interest is compounded, we will assume it is compounded annually (n = 1).
After 6 years, the formula becomes:
\(A = 220(1 + 0.042/1)^{(1*6)}A = 220(1.042)^6\)
A = 220(1.2835)
A = $282.37
Therefore, Molly earned $282.37 - $220.00 = $62.37 in interest at the end of six years.
Learn more about compound interest, by the following link
https://brainly.com/question/24924853
#SPJ4
what does the slope of a beer's law plot represent
Answers
The slope of a beer's law plot represents that one can quantitatively determine the molar absorptivity of a substance, which is essential for accurately determining concentrations of unknown samples using spectrophotometric methods.
In Beer's law, the relationship between the concentration of a substance and its absorbance is described by the equation A = εbc, where A is the absorbance, ε is the molar absorptivity (also known as the molar absorptivity coefficient), b is the path length of the sample, and c is the concentration of the substance.
When plotting a graph of absorbance versus concentration, the slope of the line represents the molar absorptivity (ε). The molar absorptivity is a constant that reflects the substance's ability to absorb light at a specific wavelength. A higher molar absorptivity indicates that the substance has a greater tendency to absorb light and is more sensitive to changes in concentration.
Conversely, a lower molar absorptivity indicates weaker absorption characteristics.
In summary, by measuring the slope of the Beer's law plot, one can quantitatively determine the molar absorptivity of a substance.
To know more about Beer's law, refer here:
https://brainly.com/question/30762062#
#SPJ11
Write the equation of the line through each point. Use slope-intercept form.
(-2,1) ; perpendicular to 3 x+y=1
Answers
The equation of the line in slope-intercept form passing through the point (-2 , 1) and perpendicular to 3x + y = 1 is y = (1/3)x + 5/3.
The equation of a line can be expressed in three different forms: standard form, slope-intercept form, and point-slope form.
The slope-intercept form of the equation of a line is given by the formula:
y = mx + b
where m is the slope of the line
b is the y- intercept
If the line is perpendicular to 3x + y = 1, then their slopes are negative reciprocal of one another. To get the slope, m, of the equation, express it in slope-intercept form.
3x + y = 1
y = -3x + 1
m = -3
m = 1/3
Substitute the values of the slope and the point to solve for the y-intercept, b.
y = mx + b
1 = 1/3(-2) + b
b = 5/3
Write the equation of the line by plugging in the value of the slope and y-intercept.
y = mx + b
y = (1/3)x + 5/3
To learn more about equation of the line in slope-intercept form: brainly.com/question/1884491
#SPJ4

14. Subtract: 5 - 3 1/3.
A. 313
B.223
C. 12/3
D.23
Answers
Answer:
The answer is 1 \(\frac{2}{3}\)
The work is shown on the picture.
Step-by-step explanation: Hope this helps and mark brainliest if ya want :)!

1. In a linear programming problem, the binding constraints for the optimal solution are5X + 3Y ≤ 302X + 5Y ≤ 20a. Fill in the blanks in the following sentence:As long as the slope of the objective function stays between _______ and _______, the currentoptimal solution point will remain optimal.b. Which of these objective functions will lead to the same optimal solution?explain1) 2X + 1Y 2) 7X + 8Y 3) 80X + 60Y 4) 25X + 35Y2.The binding constraints for this problem are the first and third.Min x1 + 2x2s.t . x1 + x2 ≥ 3002x1 + x2 ≥ 4002x1 + 5x2 ≤ 750x1 , x2 ≥ 0a. Keeping c2, fixed at 2, over what range can c1 vary before there is a change in the optimal solutionpoint?b. Keeping c1 fixed at 1, over what range can c2 vary before there is a change in the optimal solutionpoint?c. If the objective function becomes Min 1.5x1 + 2x2, what will be the optimal values of x1, x2, and theobjective function?3.
Answers
1. a. The slope of the objective function needs to be between -5/3 and -2/5 in order for the current optimal solution point to remain optimal.
b. All of these objective functions will lead to the same optimal solution because they have the same slope (-5/3).
2.a. The range for c1 can vary between -1/3 and 1/3 without a change in the optimal solution point.
b. The range for c2 can vary between 2/5 and infinity without a change in the optimal solution point.
c. The optimal values of x1 = 100 and x2 = 200, with an objective function value of 500.
a) The slope of the objective function is the ratio of the coefficient of x2 to the coefficient of x1, i.e., slope = c2/c1. The optimal solution point will remain optimal as long as the slope of the objective function stays between the slopes of the binding constraints.
For the given problem, the slopes of the binding constraints are:
5X + 3Y = 30 => slope = -5/3
2X + 5Y = 20 => slope = -2/5
Therefore, as long as the slope of the objective function stays between -5/3 and -2/5, the current optimal solution point will remain optimal.
b) To determine which objective functions will lead to the same optimal solution, we need to find the corner points of the feasible region and evaluate each objective function at those points. The optimal solution will be the corner point that minimizes (or maximizes) the objective function.
The corner points of the feasible region are:
(0, 400)
(150, 150)
(250, 0)
Evaluating the objective functions at these corner points, we get:
2X + 1Y => 0, 550, 500
7X + 8Y => 3200, 1550, 0
80X + 60Y => 48000, 36000, 25000
25X + 35Y => 10500, 8250, 7000
Therefore, objective functions 1 and 4 will lead to the same optimal solution, which is at the corner point (150, 150), where x1 = 150, x2 = 150, and the objective function value is 8250.
c) To solve the problem using the new objective function Min 1.5x1 + 2x2, we need to solve the system of inequalities:
x1 + x2 ≥ 300
2x1 + x2 ≥ 400
2x1 + 5x2 ≤ 750
x1, x2 ≥ 0
and minimize the objective function 1.5x1 + 2x2.
The corner points of the feasible region are:
(0, 400)
(200, 100)
(375, 0)
Evaluating the objective function at these corner points, we get:
(0, 400) => 800
(200, 100) => 500
(375, 0) => 562.5
Therefore, the optimal values are x1 = 200, x2 = 100, and the objective function value is 500.
Learn more about linear programming click here:
brainly.com/question/25828237
#SPJ11
how to write cube root on mobius
Answers
The radius sign () with a little three (3) above it, followed by the number, can be used to represent a number's cube root. For instance, 8's cube root is represented by the symbol 8.
The number that remains the same after being multiplied twice by itself is known as a number's cube root. It can be written as the radical sign () followed by the number and a little three (3) above it. For instance, 8's cube root is represented by the symbol 8. When 8 is multiplied by itself twice (8 x 8 x 8), the result is 8; this is known as "the cube root of 8." In a similar way, 27's cube root can be expressed as 27, which, when multiplied by itself twice, also equals 27. Exponential expressions can also be used to represent cube roots. Because 8's cube root is expressed as 23, the result of multiplying 8 by itself three times (2 x 2 x 2) is also 8. Similarly, 33 can be used to represent the cube root of 27.
Learn more about radius here
https://brainly.com/question/15047456
#SPJ4
since 15 percent of a university comprises asian-american students, a sample for a study was chosen in such way that it, too, consisted of 15 percent asian-americans. this kind of sample would be an example of a .
Answers
The kind of sample that consists of the same percentage of Asian-American students as the population it is taken from is called a representative sample.
A representative sample is a subset of a population that accurately reflects the characteristics and proportions of the entire population. In this case, the population consists of 15% Asian-American students. By selecting a sample that also consists of 15% Asian-American students, it can be considered a representative sample.
A representative sample is important in statistical research because it allows for generalizations and inferences to be made about the population based on the characteristics observed in the sample. Ensuring that the sample reflects the population proportions, it increases the likelihood of obtaining accurate and reliable results.
Choosing a representative sample is crucial to minimize bias and ensure the validity of the study's findings. It helps to avoid underrepresentation or overrepresentation of certain groups within the population, which can lead to misleading or inaccurate conclusions. Therefore, selecting a sample that consists of the same percentage of Asian-American students as the population is an example of a representative sample.
Learn more about representative sample here:- brainly.com/question/32150032
#SPJ11
find the remainder when f(x) = 2x3 − 12x2 11x 2 is divided by x − 5. (2 points) 7 −3 3 −7
Answers
The remainder when f(x) = 2x3 - 12x2 + 11x + 2 is divided by x - 5 is 7.
We can use the remainder theorem to find the remainder when a polynomial is divided by a linear factor.
The remainder theorem states that the remainder when a polynomial f(x) is divided by x - a is f(a). In this case, the polynomial is f(x) = 2x3 - 12x2 + 11x + 2 and the linear factor is x - 5. So, the remainder is f(5).
To find f(5), we can simply substitute x = 5 into the polynomial. This gives us f(5) = 2(5)3 - 12(5)2 + 11(5) + 2 = 7.
Therefore, the remainder when f(x) = 2x3 - 12x2 + 11x + 2 is divided by x - 5 is 7.
Learn more about remainder theorem here:
brainly.com/question/30242665
#SPJ11
Can anyone factor these questions?

Answers
10) The factor of the expression (x³ + 7x² + 6x) is,
⇒ x (x + 1) (x + 6)
11) The value of a in factor of (x² - 16x + 63) is, - 9
What is an expression?Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
We have to given that;
10) The expression is,
⇒ x³ + 7x² + 6x
11) The expression is,
⇒ x² - 16x + 63
Now, We can factor as;
10) The expression is,
⇒ x³ + 7x² + 6x
⇒ x (x² + 7x + 6)
⇒ x (x² + 6x + x + 6)
⇒ x (x (x + 6) + 1 (x + 6))
⇒ x (x + 1) (x + 6)
11) The expression is,
⇒ x² - 16x + 63
⇒ x² - 9x - 7x + 63
⇒ x (x - 9) - 7 (x - 9)
⇒ (x - 7) (x - 9)
Hence, By compare the factors (x - 7) (x + a), we get;
⇒ a = - 9
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ1
An ice cream stand sells three different flavors of ice cream: vanilla, chocolate, and strawberry. Each gallon of vanilla costs $6.00 to purchase, each gallon of chocolate costs $6.50 to purchase, and each gallon of strawberry costs $7.00 to purchase. On average, the stand has 8 gallons of vanilla, 6 gallons of chocolate, and 4 gallons of strawberry in inventory and 1.5 days-of-supply. Each gallon of ice cream serves 16 customers, on average. How many customers does the ice cream stand expect to serve each day?
Answers
The ice cream stand expects to serve 288 customers each day.
To calculate the expected number of customers the ice cream stand expects to serve each day, we need to multiply the gallons of each flavor by the number of customers served per gallon and then sum up the results.
Let's denote:
V = Gallons of vanilla = 8
C = Gallons of chocolate = 6
S = Gallons of strawberry = 4
D = Days-of-supply = 1.5
Serving per gallon = 16
The number of customers served each day can be calculated as follows:
Total customers = (V * Serving per gallon) + (C * Serving per gallon) + (S * Serving per gallon)
Total customers = (8 * 16) + (6 * 16) + (4 * 16)
Total customers = 128 + 96 + 64
Total customers = 288
To determine the number of customers served each day, we need to multiply the gallons of each flavor by the number of customers served per gallon and sum up the results. In this case, the stand has 8 gallons of vanilla, 6 gallons of chocolate, and 4 gallons of strawberry. Given that each gallon serves an average of 16 customers, we can calculate the number of customers served for each flavor by multiplying the gallons by the serving per gallon. Finally, by summing up the customers served for each flavor, we obtain the total number of customers served per day, which in this case is 288.
Learn more about customers here:-
https://brainly.com/question/29255658
#SPJ11
Find a ∩ b if a = {2, 5, 8, 11, 14} and b = {1, 3, 5, 7}. {1, 2, 3, 5, 7, 8, 11, 14} {5}
Answers
The intersection of given set a and b is a∩b = {5}.
According to the given question.
We have two sets a and b.
a = {2, 5, 8, 11, 14}
And, b = {1, 3, 5, 7}
As, we know that "the intersection of two sets A and B is the set of all those elements which are common to both A and B. Symbolically, we can represent the intersection of A and B as A ∩ B".
Since, only the element which is common to set a and set b is 5.
Thereofore, the intersection of given set a and b is given by
a∩b = {5}
Find out more information about intersection of sets here:
https://brainly.com/question/14679547
#SPJ4
a pilot flew 1308.3 miles this week The pilot flew the same number of miles each of 3 days this week. How many miles did the pilot fly each day?
Answers
Answer:
Step-by-step explanation:
The pilot flew 436.1 miles each day.
Stella is using her compass and straightedge to complete a construction of a polygon inscribed in a circle. which polygon is she in the process of constructing? a circle is drawn with five arc markings that lie on the circle, with an additional point also marked on the circle. a regular octagon a square a regular pentagon a regular hexagon
Answers
The polygon is a regular hexagon.
Stella is using a compass and a straight edge to construct a polygon inscribed in a circle.
Also the circle is drawn with five arc markings that lie on the circle. Also there is an additional point marked on the circle.
So there are in total 6 points on the circle. Also the lines joining these five points will be equal. So we will get a regular hexagon through this construction.
The following is the process of construction.
First she starts at a point on the circle placing the compass there. Then she will measure the radius of the circle on compass. Fixing this distance, she will draw an arc on the circle. The process is repeated by placing the compass on the new point obtained on the circle.
So in total she will get the 6 vertexes of the regular hexagon. Joining the adjacent points, a regular hexagon is inscribed inside the circle.
Learn more about constructions using compass and straight edge at https://brainly.com/question/8150473
#SPJ4
Answer: A regular hexagon
2
Which expression is equivalent to -6[
==(-3-2012
0 -4 -12%
0 - 4 + 2%
o 4-12%
o 4+ 12%
first answer gets best marks

Answers
Answer:
C
Step-by-step explanation:
-6(-2/3 + 2x)
= 12/3 = 4
4 is the answer to the first number times -6. This is because 2 negatives are equal to a positive.
-6 * 2x
= -12
So, it can be concluded that the answer is C
-8(6-r)=24 what is the solution for r
Answers
Answer:hi
Step-by-step explanation:Let me first warn you that I CANNOT get the denominators of this problem to go underneath the numerators. It looks good on my answer page but when I click "preview your answer" the denominators are ALL over the place. Grrrrr.
I think the weirdly placed denominators make this explanation hard to understand but you give this a go and see if you understand things. If it is too hard to see, maybe this website will let you instant message me or email me. If so, then I will send you the solution via email. I'm very sorry the denominators are SO scattered.
See what you think of the explanations below but it might help if you write down my answer on paper, so that you can move the number to rest more closely under their proper numerators. :-)
Ok then......
Let's start with your first problem. A quick way to do this work is to cross multiply. Here's what I mean:
__3___ = __6___
r - 1 r + 2
Ok, so you can cross multiply:
3(r + 2) = 6(r - 1) (cross multiply)
3r + 6 = 6r - 6 (use the distributive property)
Now you will have to put the "r" variables on the left side of the equal sign and numbers without variables on the right side of the equal sign. To get 6r from the right side to the left, you can subtract 6r from the right side. If you subtract it from the right, you must subtract it from the left.....
To get 6 from the left side to the right, you can subtract it from the left. If you subtract it from the left, you must subtract it on the right.....
So now you have:
3r - 6r = -6 - 6 This becomes.........
- 3r = -12
Now to solve for "r" you will have to divide by -3. Why? Well, -3r is really saying: -3 times r. The -3 and the r are actually being multiplied together so to isolate the "r" you have to sort of "undo" the multiplication. What is the opposite of multiplication? It's DIVISION. Soooo, you must divide by -3 on both sides. SO you have:
- 3r = -12
r = 4 (-12 divided by -3 is a positive 4)
Now you know "r" equals 4. If we "plug" 4 back into the original equation, we can see the answer is correct. Check this out:
__3___ = __6___ (original equation)
r - 1 r + 2
__3___ = __6___ (substitute "4" in for "r"
4 - 1 4 + 2
__3___ = __6___ (do the math in the denominator area)
3 6
1 = 1 (3/3 equals 1 and 6/6 also equals 1, so our
solution that r = 4 is correct!) :-)
Now to your 2nd problem..........
4/2x-5 = 24/2x
___4___ = __24___
2x � 5 2x
Let's cross multiply again:
4(2x) = 24(2x - 5)
8x = 48x - 120
8x - 48x = - 120
-40x = - 120
(divide both sides by -40)
x = 3
Now let's "plug" 3 in where we had the variable "x" in the original equation to see if we are correct.
___4___ = __24___ (original equation)
2x � 5 2x
___4___ = __24___ (substituted 3 for "x")
2(3) � 5 2(3)
___4___ = __24___
6 - 5 6
___4___ = __24___
1 6
4 = 4
SO once again we have found the correct answer. Yay for us! :-)
I hope this helps. :-)
Answer:
\(r=9\)
Step-by-step explanation:
So we have the equation:
\(-8(6-r)=24\)
Divide both sides by -8:
\(6-r=-3\)
Subtract 6 from both sides:
\(-r=-9\)
Divide both sides by -1:
\(r=9\)
And we're done!
a binary tree is a structure in which each node is capable of having successor nodes, called .
Answers
A binary tree is a structure in which each node is capable of having two successor nodes, called "left child" and "right child."
In a binary tree, each node can have at most two successor nodes, known as the left child and the right child. These successor nodes branch out from the parent node, forming two distinct paths or branches. The left child represents the left branch, and the right child represents the right branch. This hierarchical structure allows for efficient organization and traversal of data, as each node can connect to two other nodes, creating a branching pattern throughout the tree. The concept of left and right children enables various operations and algorithms to be performed on the binary tree, such as insertion, deletion, searching, and sorting.
To know more about binary tree,
https://brainly.com/question/33461694
#SPJ11
Please help!! 50 POINTS!! Explain how you got each answer:
1. What is the growth rate for a country that has a total population of 11,000,000 with 320,000 births and 650,000 deaths?
2. What is the growth rate for a country that has 60,000 births and 50,000 deaths per year along with 20,000 people who immigrate in and 10,000 people who emigrate out? The total population is 20,000,000.
3. Belgium has a growth rate of 0.1% In how many years will it double its population?
4. Libya is doubling its population every 19 years. What is the growth rate?
Answers
Answer:
To find the growth rate for a country with a population of 11,000,000, 320,000 births, and 650,000 deaths, you need to first calculate the natural increase in the population by subtracting the number of deaths from the number of births: 320,000 - 650,000 = -330,000. This means that there are 330,000 more deaths than births in this country.
To calculate the growth rate, you need to divide the natural increase by the total population and multiply by 100 to express the result as a percentage. In this case, the growth rate would be: (-330,000 / 11,000,000) * 100 = -3.0%. This means that the population is decreasing at a rate of 3.0% per year.
To find the growth rate for a country with 60,000 births, 50,000 deaths, 20,000 immigrants, and 10,000 emigrants, you need to first calculate the natural increase in the population by subtracting the number of deaths from the number of births: 60,000 - 50,000 = 10,000. Then, you need to add the number of immigrants to this number to get the total increase in the population: 10,000 + 20,000 = 30,000. Finally, you need to subtract the number of emigrants from this number to get the net increase in the population: 30,000 - 10,000 = 20,000.
To calculate the growth rate, you need to divide the net increase in the population by the total population and multiply by 100 to express the result as a percentage. In this case, the growth rate would be: (20,000 / 20,000,000) * 100 = 0.1%. This means that the population is increasing at a rate of 0.1% per year.
Belgium has a growth rate of 0.1%, which means that its population is increasing by 0.1% per year. To find out how many years it will take for the population to double, you need to divide the growth rate into the number 100. Since 100 / 0.1 = 1000, it will take 1000 years for Belgium's population to double if it continues to grow at a rate of 0.1% per year.
Libya is doubling its population every 19 years, which means that its population is increasing by 100% every 19 years. To find the growth rate, you need to divide the population increase (100%) by the number of years it takes for the population to double (19 years) and multiply by 100 to express the result as a percentage. In this case, the growth rate would be: (100 / 19) * 100 = 5.26%. This means that Libya's population is increasing at a rate of 5.26% per year.
Step-by-step explanation:
8 apples cost $1.44 how mucho is 1 cost
Answers
Answer:
$0.18
Step-by-step explanation:
apple(s) : price
8 : $1.44
4 : $0.72
2 : $0.36
1 : $0.18
PLLLLLEEEAAAAASSSSEEE ANSWER NEED HELP!!!!!!!!!!!!!!!!!!!!!! WILL MARK 5 STARS!!!!!!!!!!!!!!!!

Answers
Answer:
UT = 8
Step-by-step explanation:
From the picture, we can make the following equation...
5 + 2x - 6 = x + 6
By solving it we get
5 + 2x - 6 = x + 6
2x - 1 = x + 6
2x = x + 7
x = 7
Therefor if UT = 2x - 6, then UT is equal to...
2x - 6 = UT
2(7) - 6 = UT
14 - 6 = UT
8 = UT
Carlos is picking 6/384 apples. Mateo is picking oranges of 10. How much did Mateo pick?
Answers
Question might be incomplete or incorrect so we'd have to assume Mateo took apples
Answer:
5/189 apples
Step-by-step explanation:
If Carlos picks 6/384 apples then there must be 384 apples available to pick from. Amount of apples left after Carlos picks =384-6=378 apples
If Mateo picks 10 apples after Carlos then how much apples Mateo has taken would depend on the number of apples available, hence the fraction of apples Mateo has taken = 10/378
Reduce to lowest terms to get 5/189 apples
The weight, in pounds, of a certain type of adult squirrel is normally distributed with a mean of 4. 1 pounds and a standard deviation of 0. 5 pounds. What is the probability that a randomly selected squirrel has a weight less than 3 pounds? round your answer to four decimal places.
Answers
The percentage of squirrels that have a weight between 3 and 5 pounds is; 95.017%
What is percentage?In mathematics ,a percentage is a number that can be expressed as a fraction of 100. If you need to calculate the percentage of a number, divide the number by the whole number and multiply by 100. Percentages therefore mean 1 in 100. If you need to convert a decimal number like 0.57 to percent just multiply by 100 So 0.57 x 100 = 57. So as a percentage, 0.57 equals 57%. Percentage can be calculated by dividing the value by the total and multiplying the result by 100. The formula used to calculate the percentage is (value/total) x 100%.To learn more about percentage from the given link :
https://brainly.com/question/2155156
#SPJ4
help me with this please

Answers
The values of a, b, c are 152°, 28°, 152° respectively.
What are angle at a point?Angles around a point describes the sum of angles that can be arranged together so that they form a full turn.
The sum of angles at a point will give 360°.
This means that a + b + c + 28 = 360
c +28 = 180° ( angle on a straight line)
c = 180 -28
c = 152°
c = a( alternate angles are equal)
therefore the value of a = 152°
b = 28( alternate angles are equal)
therefore the value of b is 28
therefore the values of a, b, c are 152°, 28°, 152° respectively
learn more about angle at a point from
https://brainly.com/question/25716982
#SPJ1
Convert 2/5
into a percentage and choose the appropriate result.
A 20%
B) 40%
C 30%
D) 60%

Answers
Answer:
B.) 40%
Step-by-step explanation:
2/5 = 4/10 = 0.4
0.4 x 100% = 40%
Ion get this bro someone help I got school in a hour

Answers
Answer:
of Example 6
5 and 14
Step-by-step explanation:
IN EXAMPLE 6
Opposite angles are equal so you equate the first one like this
3x + 20 = 10x - 15
15 + 20 = 7x
35/7 = x
x = 5
In next question b
It is a straight line thus it's 180°
so 4n + 22 +8n -10 = 180
12n + 12 = 180
12n = 180 - 12
n =168÷ 12
n = 14
) The value of shares, t years after their floatation on the stock market, is modelled by V=10e 0.09t
Find the initial value of these shares and values after 5 years, 10 years and 12 years, respectively. Round your answer to two decimal places. [9 marks] During a recession, a firm's revenue declined continuously so that the total revenue (TR) in t years' time is modelled as TR=10e −0.19t
(in million dollars) Calculate the current revenue and revenue in 5 years' time. After how many years the revenue of this firm is going to drop to $1 million? Round your answer to two decimal places.
Answers
After approximately 12.13 years, the revenue of this firm is going to drop to $1 million.
The value of shares t years after their floatation on the stock market, is modelled by V = 10e0.09t
The initial value of shares = V when t = 0. So, putting t = 0 in V = 10e0.09t,
we get
V = 10e0.09 × 0= 10e0 = 10 × 1 = 10 million dollars.
The values after 5 years, 10 years and 12 years, respectively are:
For t = 5, V = 10e0.09 × 5 ≈ 19.65 million dollarsFor t = 10, V = 10e0.09 × 10 ≈ 38.43 million dollarsFor t = 12, V = 10e0.09 × 12 ≈ 47.43 million dollars
The total revenue (TR) in t years' time is modelled as TR = 10e−0.19t (in million dollars)
The current revenue is the total revenue when t = 0.
So, putting t = 0 in TR = 10e−0.19t, we get
TR = 10e−0.19 × 0= 10e0= 10 million dollars
Revenue in 5 years' time is TR when t = 5.
So, putting t = 5 in TR = 10e−0.19t, we get
TR = 10e−0.19 × 5≈ 4.35 million dollars
To find when the revenue of this firm is going to drop to $1 million, we need to solve the equation TR = 1.
Substituting TR = 1 in TR = 10e−0.19t, we get1 = 10e−0.19t⟹ e−0.19t= 0.1
Taking natural logarithm on both sides, we get−0.19t = ln 0.1 = −2.303
Therefore, t = 2.303 ÷ 0.19 ≈ 12.13 years.
So, after approximately 12.13 years, the revenue of this firm is going to drop to $1 million.
Know more about revenue:
https://brainly.com/question/27325673
#SPJ11
You go to the park on a windy day to fly a kite. You have released 40 feet of string. The string
makes an angle of 36° with the ground. How high is the kite in the air? Round your answer to the
nearest tenth
Answers
The height of the kite is approximately 27.3 feet.
In this problem, we are given the length of the released string and the angle it makes with the ground. We need to find the height of the kite above the ground. We can solve this problem by using the tangent function in trigonometry.The tangent of an angle in a right triangle is defined as the ratio of the opposite side to the adjacent side.
In this case, the height of the kite is opposite to the angle, and the released string is adjacent to the angle. Therefore, we can set up a proportion using the tangent function and solve for the height of the kite.
The formula for the tangent function is: tan(θ) = opposite / adjacentIn our problem, the angle θ between the kite's string and the ground is 36°.
The length of the released string is 40 feet. Therefore, we can write:tan(36°) = height / 40 feetWe need to solve for the height of the kite, which is the unknown variable.
Rearranging the formula gives us:height = 40 feet × tan(36°).Using a calculator, we can evaluate tan(36°) to be approximately 0.7265.
Plugging in the values to the formula gives us:height = 40 feet × 0.7265height ≈ 29.06 feetRounding this answer to the nearest tenth gives us:height ≈ 27.3 feet.
Therefore, the height of the kite is approximately 27.3 feet.
The height of the kite can be found using the tangent function in trigonometry. We set up a proportion between the height of the kite and the length of the released string, with the angle between the kite's string and the ground being the included angle. We solved for the height of the kite by rearranging the formula and plugging in the values. The height of the kite was found to be approximately 27.3 feet.
To know more about tangent function visit:
brainly.com/question/30162652
#SPJ11
Consider this expression. - 4 x 2 + 2 x − 5 ( 1 + x ) What expression is equivalent to the given expression? x 2 + x +
Answers
The expression equivalent to\(-4x^2 + 2x - 5(1 + x)\) is \(4x^2 + 8x + 5.\)
This expression matches the form \(x^2 + x + c,\) where c = 5.
To simplify the given expression \(-4x^2 + 2x - 5(1 + x)\) and make it equivalent to the expression \(x^2 + x + c,\) where c is a constant term, we need to perform some algebraic operations.
First, let's distribute the -5 to the terms inside the parentheses:
\(-4x^2 + 2x - 5 - 5x\)
Next, we can combine like terms:
\(-4x^2 + (2x - 5x) - 5 - 5x\)
Simplifying further:
\(-4x^2 - 3x - 5 - 5x\)
Now, let's rearrange the terms to match the form \(x^2 + x + c:\)
\(-4x^2 - 3x - 5x - 5\)
To make the leading coefficient positive, we can multiply the entire expression by -1:
\(4x^2 + 3x + 5x + 5\)
Now, we can combine the x-terms:
\(4x^2 + 8x + 5\)
So, the expression equivalent to \(-4x^2 + 2x - 5(1 + x)\) is \(4x^2 + 8x + 5.\)This expression matches the form \(x^2 + x + c,\) where c = 5.
It's important to note that the original expression and the equivalent expression have different coefficients and constants, but they represent the same mathematical relationship.
For similar question on expression.
https://brainly.com/question/723406
#SPJ8
What is an equivalent equation to 1/4n-16
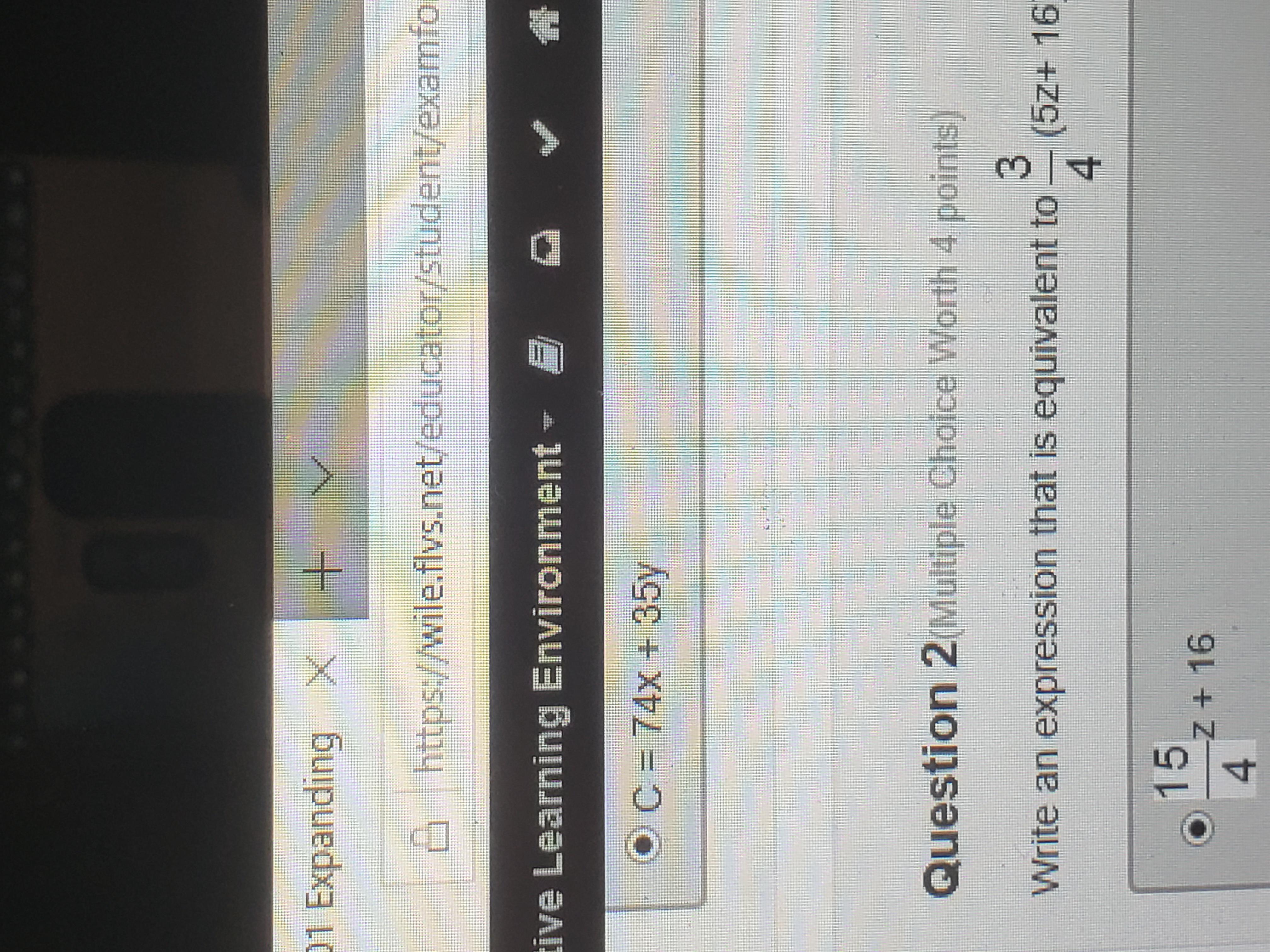
Answers
Answer:
15/4z+12
Step-by-step explanation: