The height of a cone is twice the radius of its base. a cone has a height of 2 x and a radius of x. what expression represents the volume of the cone, in cubic units? two-thirdsπx3 four-thirdsπx2 2πx3 4πx3
Answers
The expression that represents the volume of the cone, in cubic units, is (2/3) * π * x^3. Option a is correct choice.
The formula for the volume of a cone is,
V = (1/3) * π * r^2 * h
where V is the volume, r is the radius, h is the height, and π is a mathematical constant approximately equal to 3.14159.
In this case, the height of the cone is 2x and the radius is x, so we can substitute these values into the formula,
V = (1/3) * π * x^2 * (2x)
Simplifying this expression gives:
V = (2/3) * π * x^3
Option a is correct.
To know more about volume, here
https://brainly.com/question/13688836
#SPJ4
--The complete question is, The height of a cone is twice the radius of its base. a cone has a height of 2 x and a radius of x. what expression represents the volume of the cone, in cubic units?
a. (2/3) * π * x^3
b. (4/3) * π * x^3--
Related Questions
x2 + 5x - 36 which binomial is a factor of the polynomial?
Answers
Thus, the two binomials that are factor of the polynomial are $(x + 9)$ and $(x - 4)$.
3x-5=16
find x pls hurry
Answers
please answer this question

Answers
The value of m<2 = 107
Given:
m<SOX = 160
m<1 = x+14
m<2 = 3x - 10
x + 14 + 3x - 10 = 160
4x + 14 - 10 = 160
4x + 4 = 160
4x = 160 - 4
4x = 156
divide by 4 on both sides
4x/4 = 156/4
x = 39
m<2 = 3*39 - 10
= 117 - 10
= 107
Learn more about the value here:
https://brainly.com/question/14316282
#SPJ1
If f is any function, then the associated Green's Function G[f] is given by G[f](x) = integral ^x_0 f(s) sin(x - s)ds. Use variation of parameters to show that G[f] is a solution of y" + y = f(x).
Answers
We have: u''(x) = ƒ(x)cot(x) - 2u'(x)cot(x).Thus, we can find a particular solution of this differential equation by using variation of parameters.
Let G(x) = ƒ(s)sin(x - s) ds.
Then, by the product rule, we have: G' = ƒ(s)cos(x - s) ds - ƒ(s)sin(x - s) ds, and G'' = -ƒ(s)sin(x - s) ds - ƒ(s)cos(x - s) ds. Hence, we have:G'' + G = ƒ(s)sin(x - s) ds - ƒ(s)cos(x - s) ds + ƒ(s)sin(x - s) ds = ƒ(s)sin(x - s) ds = G.
So, G is indeed a solution of y'' + y = ƒ(x).Next, we will use variation of parameters to find a second solution of the same differential equation.
Let us suppose that we have another solution of the form y = u(x) sin(x).
Then, y' = u(x)cos(x) + u'(x)sin(x), and y'' = - u(x)sin(x) + 2u'(x)cos(x) + u''(x)sin(x).
Substituting these into the differential equation, we get:- u(x)sin(x) + 2u'(x)cos(x) + u''(x)sin(x) + u(x)sin(x) = ƒ(x)2u'(x)cos(x) + u''(x)sin(x) = ƒ(x)
Dividing by sin(x), we get:2u'(x)cot(x) + u''(x) = ƒ(x)cot(x).
Now, let us assume that the second solution is of the form y = u(x)sin(x), where u is a function to be determined.
Then, we have: y' = u(x)cos(x) + u'(x)sin(x) and y'' = - u(x)sin(x) + 2u'(x)cos(x) + u''(x)sin(x).
Substituting these into the differential equation, we get: - u(x)sin(x) + 2u'(x)cos(x) + u''(x)sin(x) + u(x)sin(x) = ƒ(x)2u'(x)cos(x) + u''(x)sin(x) = ƒ(x)
Dividing by sin(x), we get:2u'(x)cot(x) + u''(x) = ƒ(x)cot(x).
Hence, we have: u''(x) = ƒ(x)cot(x) - 2u'(x)cot(x).Thus, we can find a particular solution of this differential equation by using variation of parameters.
Know more about differential equation here,
https://brainly.com/question/32538700
#SPJ11
what is the correlation

Answers
Answer: moderate, C, B
Step-by-step explanation:
A) A shows a moderate negative correlation. It is moderate because the scattered points are sort of close to the line so it has moderate/medium correlation. It is also negative because it has a negative slope
B) C shows the strongest correlation because the points around the line are tight and close.
C) B should not have been drawn. The correlation is very weak. You do know where the line should be because the points are all over the place.
\(\sf x-12=14\)
Answers
X - 12 = 14
+12. +12
X = 26
F(D,C,B,A)=∑m(1,3,6,8,9,10,13,15
Answers
Given, F(D,C,B,A)=∑m(1,3,6,8,9,10,13,15)Here, F(D,C,B,A) is a boolean function and ∑m(1,3,6,8,9,10,13,15) represents the minterms of the function.A minterm is a product term containing all the variables of the function, with each variable either in direct or complemented form.
A minterm is denoted by mi, where i is the decimal equivalent of the binary number formed by the variables.A variable in the direct form is represented by the variable itself, whereas in the complemented form, it is represented by a bar over the variable.
The given minterms can be represented in terms of the variables D, C, B, and A as follows:m1: 0001 = A'BC'D'm3: 0011 = A'BC'Dm6: 0110 = A'BCD'm8: 1000 = AB'C'D'm9: 1001 = AB'C'Dm10: 1010 = AB'CD'm13: 1101 = ABC'Dm15: 1111 = ABCD'Hence, the Boolean function F(D,C,B,A) for the given minterms is:F(D,C,B,A) = A'BC'D' + A'BC'D + A'BCD' + AB'C'D' + AB'C'D + AB'CD' + ABC'D + ABCD.
Learn more about boolean function:
https://brainly.com/question/31540875
#SPJ11
In triangle DEF, CG = (x + 5) units and DG = (3x - 2) units.
Triangle D E F has centroid G. Lines are drawn from each point to the midpoint of the opposite side to form line segments D C, E B, F A.
[Figure may not be drawn to sacle]
What is DG?
12 units
17 units
34 units
51 units
Answers
Applying the centroid theorem, the length of DG in the triangle shown below is calculated as: DG = 34 units.
How to Apply the Centroid Theorem?Given the following information regarding the triangle shown in the image as follows:
G is the centroid of triangle DEF
CG = (x + 5) units
DG = (3x - 2) units.
Based on the centroid theorem, we have:
DG = 2/3(CD)
Plug in the values into the equation above:
3x - 2 = 2/3 * (x + 5 + 3x - 2)
Solve for x:
3(3x - 2) = 2 * (4x + 3)
9x - 6 = 8x + 6
9x - 8x = 6 + 6
x = 12
DG = 3x - 2 = 3(12) - 2
DG = 34 units.
Learn more about the centroid theorem on:
https://brainly.com/question/30301613
#SPJ1

which sequence of transformations could be used to move triangle RST so it completely covers triangle R”S”T?
Answers
Triangle RST is reflected across the x-axis and translated 5 units to the left to form triangle R"S"T"
What is transformation?Transformation is the movement of a point from its initial location to a new location. Types of transformation are reflection, translation, rotation and dilation.
Triangle RST is reflected across the x-axis and translated 5 units to the left to form triangle R"S"T"
Find out more on transformation at: https://brainly.com/question/4289712
#SPJ1

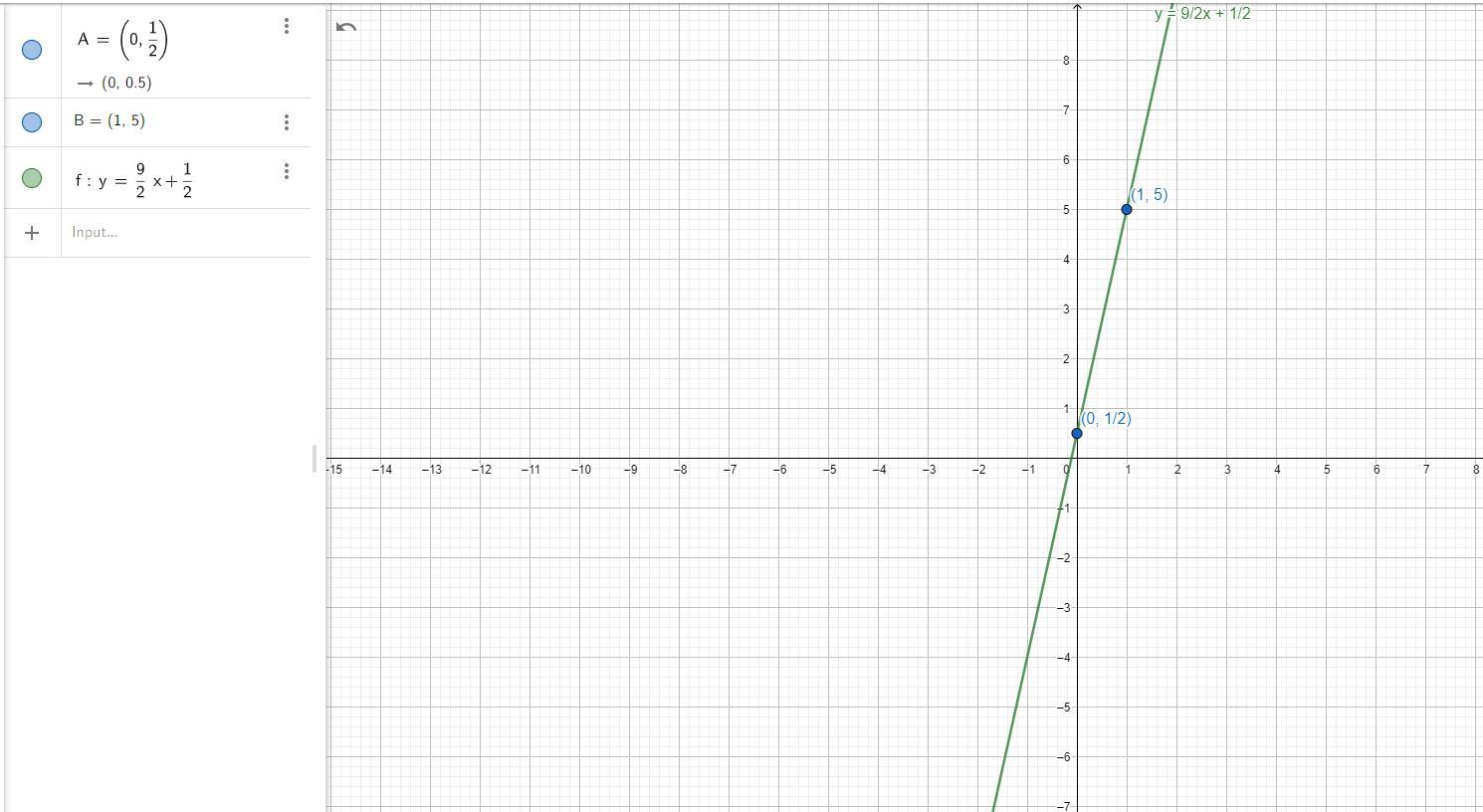
graph the linear equation using the slope intercept form . -11x+2y=1

Answers
We will have the following:
*First: We solve for y:
\(-9x+2y=1\Rightarrow2y=9x+1\)\(\Rightarrow y=\frac{9}{2}x+\frac{1}{2}\)*Second: We determine two sets of points that belong to the line. In our case we will solve for x = 0 & x = 2. So we would get:
*For x = 0:
\(y=\frac{9}{2}(0)+\frac{1}{2}\Rightarrow y=\frac{1}{2}\)So, we would have the point:
\((0,\frac{1}{2})\)*For x = 1:
\(y=\frac{9}{2}(1)+\frac{1}{2}\Rightarrow y=5\)So, we would have the point:
\((1,5)\)*Third: We graph:
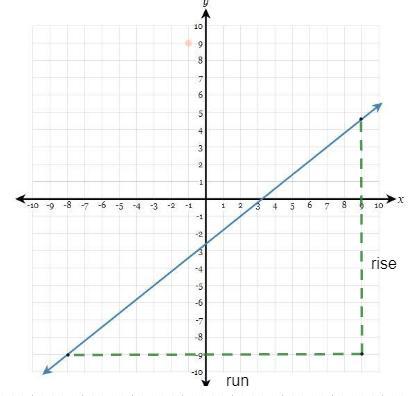
Draw a line representing the "rise" and a line representing the "run" of the line. State the slope of the line in simplest form.

Answers
The slope of the line is m = 14 / 17
The slope of a line is that the magnitude relation of quantity the quantity the number that y will increase as x will increase some amount. Slope tells you ways steep a line is, or what proportion y will increase as x will increase. The slope is constant (the same) anyplace on the road.Slope = rise/runIf y represents the vertical direction on a graph, and x represents the horizontal direction, then this formula becomes:Slope = (Change in y)/(Change in x)The line representing "rise" and " run" is given below
The vertical distance is said to be "rise" and from the graph it is equal to 14.
The horizontal distance is said to be "run" and from the graph it is equal to 17 .
According to the slope formula , we get
m = 14 / 17
Learn more about slope here :
https://brainly.com/question/13014960
#SPJ9
An automatic filling machine is used to fill 2-litre bottles of cola. The machine’s output is known to be approximately Normal with a mean of 2.0 litres and a standard deviation of 0.01 litres. Output is monitored using means of samples of 5 observations.
Determine the upper and lower control limits that will include roughly 95.5 percent of the sample means.
If the means for 6 samples are 2.005, 2.001, 1.998, 2.002, 1.995 and 1.999, is the process in control?
Answers
The upper control limit (UCL) is approximately 2.0018 litres, and the lower control limit (LCL) is approximately 1.9982 litres, which would include roughly 95.5 percent of the sample means.
Now let's check if the process is in control using the given sample means:
To determine the upper and lower control limits for the sample means, we can use the formula:
Upper Control Limit (UCL) = Mean + (Z * Standard Deviation / sqrt(n))
Lower Control Limit (LCL) = Mean - (Z * Standard Deviation / sqrt(n))
In this case, we want to include roughly 95.5 percent of the sample means, which corresponds to a two-sided confidence level of 0.955. To find the appropriate Z-value for this confidence level, we can refer to the standard normal distribution table or use a calculator.
For a two-sided confidence level of 0.955, the Z-value is approximately 1.96.
Given:
Mean = 2.0 litres
Standard Deviation = 0.01 litres
Sample size (n) = 5
Using the formula, we can calculate the upper and lower control limits:
UCL = 2.0 + (1.96 * 0.01 / sqrt(5))
LCL = 2.0 - (1.96 * 0.01 / sqrt(5))
Calculating the values:
UCL ≈ 2.0018 litres
LCL ≈ 1.9982 litres
Therefore, the upper control limit (UCL) is approximately 2.0018 litres, and the lower control limit (LCL) is approximately 1.9982 litres, which would include roughly 95.5 percent of the sample means.
Now let's check if the process is in control using the given sample means:
Mean of the sample means = (2.005 + 2.001 + 1.998 + 2.002 + 1.995 + 1.999) / 6 ≈ 1.9997
Since the mean of the sample means falls within the control limits (between UCL and LCL), we can conclude that the process is in control.
Learn more about means from
https://brainly.com/question/1136789
#SPJ11
A bottle holds
5
55 milliliters of perfume.
How many bottles can we fill with
2
22 milliliters of perfume?
Answers
Answer:
0.4 bottles can be filled
Step-by-step explanation:
divide the amount that is present by the max amount
the bottle can only hold 5.55 millimeters; therefore the max amount would be 5.55 millimeters.
the amount that is present is 2.22 millimeters.
\(\frac{222 millimeters}{555 millimeters} = 0.4\)
0.4 bottles
if the given values are 555 and 222 then the answer is still .4
Answer:
0.4 bottles can be filled
please help me with this :D

Answers
\( \color{plum}\bold{(C)} \) Diameter of circle P is the same length as the radius of circle Q.
○=> Steps to derive correct option :Given :
Diameter of circle P = 26 cm
Radius of circle P :
\( =\tt \frac{diameter}{2} \)
\( = \tt \frac{26}{2} \)
\(\color{plum} = \tt13 \: cm\)
Thus, radius of circle P = 13 cm
Diameter of circle Q = 52 cm
Radius of circle Q :
\( = \tt \frac{diameter}{2} \)
\( =\tt \frac{52}{2} \)
\( \color{plum}= \tt26 \: cm\)
Thus, radius of circle Q = 26 cm
Radius of circle R = 52 cm
Diameter of circle R :
\( =\tt radius \times 2\)
\( =\tt 52 \times 2\)
\(\color{plum} = \tt104 \: cm\)
Thus, the diameter of circle R = 104 cm
☆ Conclusion :
▪︎Diameter of circle P is the same length as the radius of circle Q.
Therefore, the correct option is (C) Diameter of circle P is the same length as the radius of circle Q.
3
Select the correct answer from each drop-down menu.
A cross section is the intersection of a __ and a __
Answers
Answer:
nolo se
Step-by-step explanation:
PLEASE I NEED THIS QUICK!!!!!
Susan wants to make pumpkin bread and zucchini bread for the school bake sale. She has 15 eggs and 16 cups of flour in her pantry. Her recipe for one loaf of pumpkin bread uses 2 eggs and 3 cups of flour. Her recipe for one loaf of zucchini bread uses 3 eggs and 4 cups of flour. She plans to sell pumpkin bread loaves for $5 each and zucchini bread loaves for $4 each. Susan wants to maximize the money raised at the bake sale. Let x represent the number of loaves of pumpkin bread and y represent the number of loaves of zucchini bread Susan bakes.
What is the objective function for the problem?
P = 15x + 16y
P = 5x + 7y
P = 5x + 4y
P = 4x + 5y
Answers
The amount of money raised can be calculated by multiplying the number of pumpkin bread loaves (x) by the selling price of each pumpkin bread loaf ($5), and adding it to the product of the number of zucchini bread loaves (y) and the selling price of each zucchini bread loaf ($4).
Therefore, the objective function for this problem is:
P = 5x + 4y
So, the correct option is:
P = 5x + 4y
If we are told ab=0, then what can we infer? by the zero product property we know = 0 = 0
Answers
If we are told that ab=0, then we can infer that either a or b (or both) must be equal to 0.
This is because when the product of two numbers is 0, at least one of the numbers must be 0 according to the zero product property.
One of the most crucial concepts for pupils to understand in maths and science is the zero product property.
The greatest educators, mathematicians, and recognized scientists in the fields of physics and chemistry have worked with Vedantu to provide their insights on the subject.
Their suggestions helped us develop materials for your understanding that would make it simple for you to put these ideas into practice.
Know more about zero product property here:
https://brainly.com/question/1626209
#SPJ11
How do you write coordinates in XY?
Answers
We use the format (x, y) to write the coordinates in format XY. Coordinates XY is a coordinate that use in Cartesian coordinate.
What is Cartesian coordinate?
Cartesian coordinate is system to draw a specific location of an unique point in the numerical condition that oriented in the two constant line where the vertical line called ordinate or Y and the horizontal line called abscess or X. The Cartesian coordinate commonly use in architecture or a design of a certain object that has a certain dilate with its original plan. This design later is use to control the construction process of the original object.
Learn more about Cartesian coordinate here
https://brainly.com/question/4726772
#SPJ4
what is the probability that it will take less than or equal to 4 throws to hit the target on both successful target hits? write out the theoretical form and use r to compute a numeric value.
Answers
The probability of hitting the target on both successful hits in 4 or fewer throws is 0.387.
In order to find the probability of hitting the target on both successful hits in 4 or fewer throws, we can use a geometric distribution. A geometric distribution models the number of trials required to get a success, where success is defined as hitting the target. Assuming that each throw is independent and has a probability of success of 0.5, the probability of getting a success on the first throw is 0.5. The probability of getting a success on the second throw is also 0.5.
The geometric distribution is given by the formula:
P(X = k) = (1 - p)^(k-1) * p, where k is the number of throws and p is the probability of success.
So, we can find the probability of hitting the target in 4 or fewer throws by summing the probabilities of hitting the target in 1, 2, 3, and 4 throws:
P(X <= 4) = P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)
= (1 - 0.5)^(1-1) * 0.5 + (1 - 0.5)^(2-1) * 0.5^2 + (1 - 0.5)^(3-1) * 0.5^3 + (1 - 0.5)^(4-1) * 0.5^4
= 0.5 + 0.25 + 0.125 + 0.0625
= 0.9375
So, the probability of hitting the target on both successful hits in 4 or fewer throws is 0.9375.
Using R, we can easily compute this numeric value:
p <- 0.5
k <- 4
sum((1 - p)^(0:(k-1)) * p)
Result:
0.3867187
To learn more about probability, visit:
https://brainly.com/question/29062095#
#SPJ11
Please Help! Ill give brainliest no fakes PLEASE!!

Answers
Answer:
4 and then 15
Step-by-step explanation:
second one: 6:4
last one: 15:10
help now please.I need to find k in simplest radical form

Answers
Answer:
2
Step-by-step explanation:
45°-45°-90° triangles are Special Right Triangles. There are some super helpful shortcuts you can learn for a 45°-45°-90° triangle.
The two legs of the triangle are always the same. The longest side, the hypotenuse, is:
hypot = leg•sqrt2
The leg in your problem is sqrt2.
You are asked to find the hypotenuse, k.
hypot = leg•sqrt2
k = leg•sqrt2
k = sqrt2•sqrt2
k = 2
k is 2. Don't be sidetracked by the direction that says "Write your answer in simplest radical form". If there was a radical in your answer, we would simplify it, but there isn't...it's just plain 2.
Avery bought 6.5 pounds of produce. If the produce was priced at $1.88 per pound, how much change did Avery receive if she paid for her purchase with a $20.00 bill?
Answers
Answer:
7.78
Step-by-step explanation:
6.5 x 1.88 = 12.22
20.00 - 12.22 = 7.78
y + 5 = –2 (x - 1) help me find the slope intercept
y - 2 = - 4 (x + 3)
Answers
Y - 2= -4(x+3) = slope intercept form is -4.000
Sabrina gets a car loan for $7,500 at 6% for 3 years. What is the principal? PLZ HELPPPP
Answers
Answer:
$41666.67
Step-by-step explanation:
Interest ×100/rate × time
7500 ×100/6×3
=$41666.67
Movie Bank is a store that rents DVDs to customers. The function m(x) = 9,000(0.62)x can be used to show the number of worldwide locations of Movie Bank x years since 2004. Which of the following statements correctly interprets the function?
Answers
The correct interpretation of the function is that it depicts the exponential rise of the number of Movie Bank worldwide locations x years since 2004, with a growth rate of 0.62.
What is the function?
A function is a rule that pairs up every element of one set, known as the domain, with a specific aspect of another set, known as the range or codomain. In other words, a function describes a relationship between two sets in which each input from the domain corresponds to exactly one output from the range.
To interpret the function correctly, we need to consider the values of x.
If x = 0, then the year 2004 is indicated because the function is expressed in terms of x years since 2004.
The base, 0.62, falls between 0 and 1, making the function an exponential growth function. In other words, the function will approach but never reach 0.
The function, for example, becomes m(1) = \(9,000(0.62)^{1}\) = 5,580 if x = 1. This indicates that around 5,580 Movie Bank locations exist in the world as of 2004, one year later.
The function will continue to increase if x is raised further but at a diminishing rate. The function, for instance, becomes m(5) = \(9,000(0.62)^{5}\) = 1,673 if x = 5. This indicates that roughly 1,673 Movie Bank locations are located throughout the world, which is significantly fewer than the previous figure, five years following the year 2004.
Therefore, the correct interpretation of the function is that it shows the exponential growth of the number of worldwide locations of Movie Bank x years since 2004, where the growth rate is 0.62.
Learn more about Functions from the given link.
https://brainly.com/question/11624077
#SPJ1
Answer:
Movie Bank locations have decreased at a rate of 38% each year since 2004.
Solve the following system of equations:
x - 2y = 14
x + 3y = 9
(12, 1)
(-1,-12)
(12,-1)
(1,12)
Answers
Work in pic:

list the next three terms in the following sequence:
1,1,2,3,5,8,.....
a.11,20,31
b.11,19,30
c.13,21,34
d.13,20,33
Answers
Answer:
the answer is c.
Step-by-step explanation:
Fibonacci sequence
When Mya looked out at the store's parking lot, she noticed that for every 4 cars, there were 6 trucks. If there's a total of 220 vehicles in the parking lot, how many of them are cars, and how many of them are trucks?
Answers
Answer:
88 cars132 trucksStep-by-step explanation:
This is a ratio problem, the ratio of cars to trucks
for every 4 cars, there are 6 trucks
represented as a ratio we have 4:6
1. how many of them are cars
applying the part to whole strategy we have
4+6 = 10
let cars be x
\(\frac{4}{10}= \frac{x}{220} \\\\x= \frac{220*4}{10} \\\\x= 880/10\\\\x= 88 cars\)
2. how many of them are trucks?
let trucks be y
\(\frac{6}{10}= \frac{y}{220} \\\\x= \frac{220*6}{10} \\\\y= 1320/10 \\\\y= 132 trucks\)
a packet of five cards consists of the ace of spades, the ace of hearts, the 2 of spades, the 3 of diamonds, and the 4 of clubs. if the packet is thoroughly shuffled, what is the probability that the two aces end up side by side? cs 2100
Answers
Answer:
there are 5
Step-by-step explanation:
dani rode her bike for 10 hours a day for 8 days . in this time she covered 576 miles. how many miles per day day did did dani average
Answers
Answer:
72 miles per day
Step-by-step explanation:
Step one data
we are told that Dani rode for 10 hours per day for 8 days
hence per day, the time taken is = 10 hours
Also,
Hence the average distance covered per day is
=total number of miles/total number of days
=576/8= 72 miles per day