The functions f(x) = x^2 – 1 and g(x) = –x^2 + 4 are shown on the graph.
Explain how to modify the graphs of f(x) and g(x) to graph the solution set to the following system of inequalities. How can the solution set be identified?
y > x^2 – 1
y ≤ –x^2 + 4

Answers
(a) Change the equation to inequality signs
(b) The solution to the system is the shaded region
How to modify the graphs of f(x) and g(x) for the solution setFrom the question, we have the following parameters that can be used in our computation:
f(x) = x² - 1
g(x) = -x² + 4
To modify the graph to determine the system of inequalities, we change the equation to inequality signs
So, we have
f(x) > x² - 1
g(x) ≤ -x² + 4
How can the solution set be identified?The solution set can be identified from the graph
From the graph, we have solution to the system to be the shaded region between the intersection of the lines
Read more about inequalities at
https://brainly.com/question/30390162
#SPJ1
Related Questions
What is an equation of the line that passes through the points (-6, -3) and
(-8,-4)
Answers
Answer:
Equation is Y=x/2
Step-by-step explanation:
Find the gradient of the line : graduent= -4-(-3)÷ -8-(-6) which = to 1\2Sustitutes any of the values of y and x coordinates and your gradient in order to find the value of c: Y =mx + c : (-4)=1/2(-8) + c then C =OY=x/2Solve the system using substitution (1 point)
x + y = 8
y = 3x
(A). (4, 12)
(B). (2, 6)
(C). (1/2, 3/2)
(D). (-4, -12)
Answers
The solution to the system is x = 2 and y = 6, represented as the ordered pair (2, 6). This corresponds to option (B) in the answer choices.
To solve the system using substitution, we'll substitute the value of one variable from one equation into the other equation and solve for the remaining variable.
Given the system:
x + y = 8
y = 3x
Substituting the value of y from the second equation into the first equation, we have:
x + (3x) = 8
4x = 8
x = 2
Now, substitute the value of x into the second equation to solve for y:
y = 3(2)
y = 6
Therefore, the solution to the system is (2, 6). Option (B) is the correct answer.
To know more about variable click here
brainly.com/question/2466865
#SPJ11
Find AC
A. 36
B. 60
C. 48
D. 12

Answers
Answer:
48
Step-by-step explanation:
AB+CB=AC which is 18+30 which is 48
Answer:
C. 48
Step-by-step explanation:
This distance of AC is the same as the distance between BC plus the distance between AB. In other words: AB + BC = AC
AB = 18
BC = 30
30 + 18 = AC
AC = 48
Tara wants to fix the location of a mountain by taking measurements from two positions 3 miles apart. From the first position, the angle between the mountain and the second position is 78o. From the second position, the angle between the mountain and the first position is 53o. Find the SHORTEST distance to the mountain. Round to the nearest hundredth of a mile (two decimal places).
Answers
Answer:
Shortest distance from the mountain is 3.17 miles.
Step-by-step explanation:
From the figure attached,
Let a mountain is located at point A.
Angle between the mountain and point B (∠B) = 53°
Angle between the mountain and point C (∠C) = 78°
Distance between these points = 3 miles
Since, m∠A + m∠B + m∠C = 180°
m∠A + 53° + 78° = 180°
m∠A = 180°- 131° = 49°
By applying sine rule in triangle ABC,
\(\frac{\text{sin}(49)}{BC}=\frac{\text{sin}(53)}{AC}= \frac{\text{sin}(78)}{AB}\)
\(\frac{\text{sin}(49)}{3}=\frac{\text{sin}(53)}{AC}= \frac{\text{sin}(78)}{AB}\)
\(\frac{\text{sin}(49)}{3}=\frac{\text{sin}(53)}{AC}\)
AC = \(\frac{3\text{sin}(53)}{\text{sin}(49)}\)
AC = 3.17 miles
\(\frac{\text{sin}(49)}{3}=\frac{\text{sin}(78)}{AB}\)
AB = \(\frac{3\text{sin}(78)}{\text{sin}(49)}\)
AB = 3.89 miles
Therefore, shortest distance from the mountain is 3.17 miles.

Answer the problem below

Answers
y = -5/4x + 5
19. When using the beta distribution, the denominator of the formula for standard deviation should be 2 sigma or twice \( 6=12 \) be just 36 be 4 sigma or four temes \( 6=24 \) be the square root of 3
Answers
The standard deviation of a beta distribution is calculated using the formula \(\(\sigma = \sqrt{\frac{\alpha \cdot \beta}{(\alpha + \beta)^2 \cdot (\alpha + \beta + 1)}}\),\) where \(\(\alpha\)\) and \(\(\beta\)\) are the parameters defining the shape of the distribution. It does not involve multiplying the sigma value by any fixed factor.
When calculating the standard deviation of a beta distribution, the denominator of the formula is not directly related to the sigma (standard deviation) parameter.
The standard deviation of a beta distribution depends on the alpha and beta parameters, which define the shape of the distribution.
The formula for the standard deviation of a beta distribution is:
\(\[ \sigma = \sqrt{\frac{\alpha \cdot \beta}{(\alpha + \beta)^2 \cdot (\alpha + \beta + 1)}} \]\)
Here, the standard deviation \((\(\sigma\))\) is calculated using the alpha and beta parameters of the beta distribution. It does not involve multiplying the sigma value by any particular factor or using a fixed denominator.
The denominator in the formula for the standard deviation of a beta distribution involves the alpha and beta parameters, which determine the shape and spread of the distribution.
It does not directly relate to the sigma value or involve multiplying sigma by a fixed factor.
To know more about beta distribution refer here:
https://brainly.com/question/29753583#
#SPJ11
Solve the following system equation graphically on the set of axes below y= x+4 and y= -3/2 - 1 PLEASE HELP MEEE
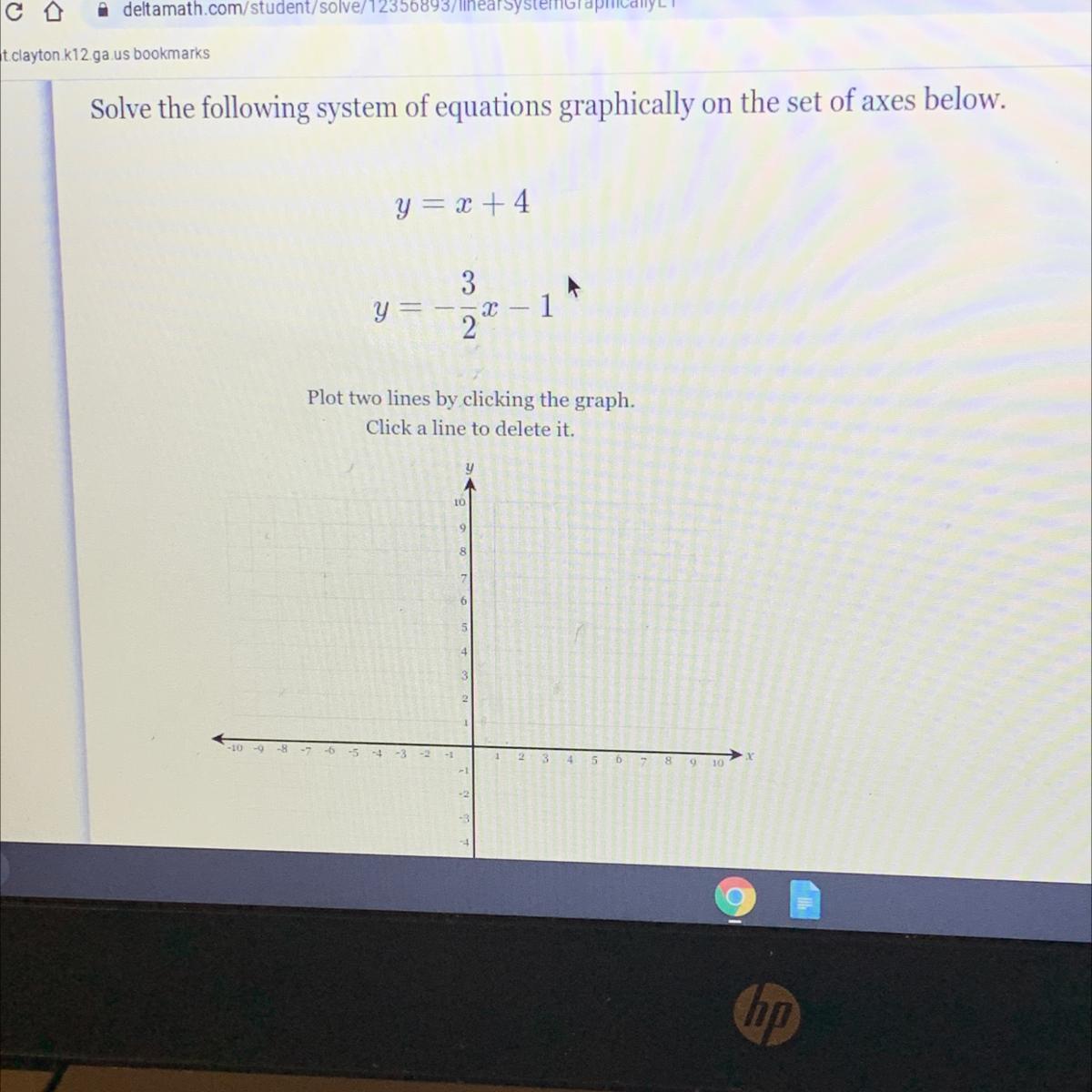
Answers
Answer:
y=4
y= -1
Step-by-step explanation:
Which triangle has an irrational number as one of its lengths

Answers
Answer:
The final/ last one's hypotenuse is the irrational one. The root there is NOT a perfect square.
Step-by-step explanation:
What is the sum of the geometric series
Answers
'' In math, a geometric series is a series with a constant ratio between successive terms.
Jason purchased a car for $22,995. According to his research, this make and model of car loses all of its marketable value after 9 years. If this car depreciates in a straight line form, what are the coordinates of the intercepts of the depreciation equation?
Answers
The car loses all of its marketable value after 9 years, the x-intercepts represent the points at which the car has lost all of its value, so they are (9, 0) and (0, 22995).
The depreciation equation for the car can be represented as y = mx + b, where y is the value of the car at time x, m is the slope of the line, and b is the y-intercept.
To find the slope, we can use the information that the car loses all of its marketable value after 9 years. The market value of the car will be 0 after 9 years, so we can set y = 0 when x = 9:
0 = m * 9 + b
To find the y-intercept, we can use the information that Jason purchased the car for $22,995. This means that the value of the car at time 0 was $22,995, so we can set y = 22,995 and x = 0:
22,995 = m * 0 + b
Combining these two equations, we can solve for m and b:
0 = m * 9 + b
22,995 = m * 0 + b
b = 22,995
Now that we have found the y-intercept, we can use it to find the x-intercepts by setting y = 0 and solving for x:
0 = m * x + 22,995
0 - 22,995 = m * x
-22,995 = m * x
x = -22,995 / m
Since we don't know the value of m, we can't find the x-intercepts directly. However, since the car loses all of its marketable value after 9 years, the x-intercepts represent the points at which the car has lost all of its value, so they are (9, 0) and (0, 22995).
To learn more about x-intercepts:
https://brainly.com/question/9110422
#SPJ4
Find the equivalent expression for (x+7)(x+1)
Answers
Answer:
x^2 + 8x + 7
Step-by-step explanation:
We can see this expression as two distributive property expressions:
(x+7)(x+1) = x(x+1) + 7(x+1)
We can then expand and combine like terms:
(x^2 + x) + (7x + 7) = x^2 + 8x + 7
We have our final answer. I hope this helps! :)
In oder for Sdumo to be able to make a decision of which offer to take,he uses a table to determine his possible income per month
Answers
a) Where the above condition exists, the dependent variable is the total income from Company A while the independent variable is the total sales.
b) The completion of Table 1 for Company A showing the total sales and total income per month is as follows:
TABLE 1: COMPANY A
Total Sales (R) Total Income(R)
$25,000 $4,000
$55,000 $8,800
$65,000 $10,400
$75,000 $12,000
$125,000 $20,000.
How do you define dependent and independent variables?
In mathematical modeling, the independent variable is the variable that is changed or controlled in order to observe its effect on the dependent variable, which is the variable being observed or measured.
TABLE 1: COMPANY A
Total Sales (R) Total Income(R)
$25,000 $4,000 ($25,000 x 16%)
$55,000 $8,800 ($55,000 x 16%)
$65,000 $10,400 ($65,000 x 16%)
$75,000 $12,000 ($75,000 x 16%)
$125,000 $20,000 ($125,000 x 16%)
TABLE 1: COMPANY B
Total Sales (R) Total Income(R)
$25,000 $8,500 ($6,000 + $25,000 x 10%)
$55,000 $11,500 ($6,000 + $55,000 x 10%)
$65,000 $12,500 ($6,000 + $65,000 x 10%)
$75,000 $13,500 ($6,000 + $75,000 x 10%)
$125,000 $18,500 ($6,000 + $125,000 x 10%)
Thus,
Company A: Commission on all sales = 16%
Company B: Basic salary = R6,000.00
Commission on all sales = 10%
Thus, if and when higher sales are recorded it pays better with Company A's offer than Company B's. But if Sdumo does not want to take risks, he might consider going for Company B's offer.
Learn more about Dependent Variables on:
https://brainly.com/question/1479694
#SPJ1
Full Question:
Although part of your question is missing, you might be referring to this full question:
Sdumo is considering two job offers, one from Company A that offers a 16% commission on all sales and another from Company B that pays a basic salary of R6,000 and an additional 10% commission on all sales. To decide which offer to take, Sdumo uses a table to determine his potential monthly income.
Dependent variable: Total Income (R)
Independent variable: Total Sales (R)
Formula for total income from Company A: Total Income = 0.16 * Total Sales
TABLE 1: COMPANY A [See attached]

Identify which of the following factoring pattern each of the following polynomials fit

Answers
EXPLANATION
Given the polynomials in the problem, we can assevere that:
Formula of Perfect Square Trinomial:
(a+b)^2 = a^2 + 2ab + b^2
Difference of Squares formula:
(a^2 - b^2)
Now, we need to find what formula match better.
y^2 + 12y - 36 -----> Neither
Bonus: double your money! One bank promises they can double your money if you invest
with them. If that were true, and you started with just 1 penny, how many doublings would you
need to reach your pennies to the moon?
Answers
Answer:
Y'all playing with me........right???
In a circle, an angle measuring 2.4 radians intercepts an arc of length 24.4. Find the radius of the circle to the nearest
Answers
The radius of the circle is approximately 10.17 units (rounded to two decimal places).
To find the radius of the circle, we need to use the formula that relates the central angle to the length of the arc and the radius of the circle. The formula is given as:
arc length = radius x central angle
In this case, the arc length is given as 24.4 and the central angle is given as 2.4 radians. Substituting these values in the formula, we get:
24.4 = r x 2.4
Solving for r, we get:
r = 24.4 / 2.4
r ≈ 10.17
To learn more about : radius
https://brainly.com/question/24375372
#SPJ11
suppose that g:a -> b and f:b -> c where a = b = c = {1, 2, 3, 4}, g ={(1, 4), (2, 1), (3, 1), (4, 2)}, and f = {(1, 3), (2, 2), (3, 4), (4, 2)}. find g o f.
Answers
The composition of functions g and f, denoted as \(\(g \circ f\)\)is a function that maps elements from the domain of f to the codomain of g. In this case, we have \(\(g: a \to b\)\) and \(\(f: b \to c\)\), where \(\(a = b = c = \{1, 2, 3, 4\}\)\).
The function g is given by \(\(\{(1, 4), (2, 1), (3, 1), (4, 2)\}\)\), and f is given by \(\(\{(1, 3), (2, 2), (3, 4), (4, 2)\}\)\). The composition \(\(g \circ f\)\) is a function that maps elements from the domain of f to the codomain of g. In other words, it combines the mappings of g and f in a way that the output of f becomes the input for g.
To compute \(\(g \circ f\)\), we start with the elements in the domain of f, which is \(\(b = \{1, 2, 3, 4\}\)\). For each element x in b, we apply f to get f(x), and then apply g to get g(f(x)).
The composition \(\(g \circ f\)\) is calculated as follows:
\(\[g \circ f = \{(1, g(f(1))), (2, g(f(2))), (3, g(f(3))), (4, g(f(4)))\}\]\)
Substituting the values from the given functions, we have:
\(\[g \circ f = \{(1, g(3)), (2, g(2)), (3, g(4)), (4, g(2))\}\]\)
Now, we substitute the values of g for the respective inputs:
\(\[g \circ f = \{(1, 2), (2, 4), (3, 2), (4, 1)\}\]\)
Therefore, the composition \(\(g \circ f\)\) is given by \(\(\{(1, 2), (2, 4), (3, 2), (4, 1)\}\)\).
To learn more about codomain refer:
https://brainly.com/question/31972943
#SPJ11
a ow network with supplies is a directed capacitated graph with potentially multiple sources and sinks, which may have incoming and outgoing edges respectively.
Answers
A flow network with supplies is a directed capacitated graph where each edge has a capacity indicating the maximum flow that can pass through it. The flow in the network represents the movement of a certain resource (e.g., water, electricity, goods) from sources to sinks.
In a flow network with supplies, there may be multiple sources, which are nodes that generate the resource and have outgoing edges, and multiple sinks, which are nodes that consume the resource and have incoming edges.
The sources and sinks can have different supply or demand values, indicating the amount of resource they generate or consume.
The edges in the flow network have capacities that restrict the maximum flow that can pass through them. The capacity represents the limit on the amount of resource that can traverse the edge. The flow through an edge cannot exceed its capacity.
The objective in a flow network is to determine the maximum flow that can be sent from sources to sinks while respecting the capacities of the edges. This is typically solved using algorithms such as the Ford-Fulkerson algorithm or the Edmonds-Karp algorithm.
The concept of a flow network with supplies is important in various applications, such as transportation networks, communication networks, and supply chain management, where resources need to be efficiently distributed from multiple sources to multiple sinks, taking into account the capacity constraints of the network.
To know more about flow network refer here:
https://brainly.com/question/29888739
#SPJ11
use this formula to find 7 (ln(x))3 dx. (use c for the constant of integration.)
Answers
The integral ∫(ln(x))^3 dx can be evaluated using integration techniques. To find the integral ∫(ln(x))^3 dx, we can use integration by substitution. Let u = ln(x), then du = (1/x) dx.
To find the integral ∫(ln(x))^3 dx, we can use integration by substitution. Let u = ln(x), then du = (1/x) dx. Rearranging, dx = x du. Substituting these values into the integral, we have:
∫(ln(x))^3 dx = ∫(u)^3 (x du) = ∫u^3 x du.
Now, we can treat x as a constant and integrate with respect to u:
= x ∫u^3 du.
Integrating u^3 with respect to u gives us:
= x * (u^4/4) + c,
where c is the constant of integration.
Substituting back u = ln(x), we have:
= x * (ln(x)^4/4) + c.
Thus, the result of the integral ∫(ln(x))^3 dx is x * (ln(x)^4/4) + c, where c is the constant of integration.
Learn more about integrate here:
https://brainly.com/question/30217024
#SPJ11
10÷2 1/4 = 10 +
= 10 x
=
Answers
Answer:
Step-by-step explanation:
56
Today, Andrew borrowed R200 000 from a bank. The bank charges interest at 5.25%p.a, a compounded quarterly. Andrew will make make payments of R6 000 at the end of 3 months. His first repayment will be made 3 months from now, how long in years will it take for Andrew to settle the loan
Answers
In order to calculate the time it will take for Andrew to settle the loan, we can use the formula for compound interest. So, it will take Andrew approximately 5.22 years to settle the loan.
The formula is given as A = P(1 + r/n)^(nt), Where: A = the final amount, P = the principal (initial amount borrowed), R = the annual interest rate, N = the number of times the interest is compounded in a year, T = the time in years.
We know that Andrew borrowed R200 000 from a bank at an annual interest rate of 5.25% compounded quarterly and that he will make repayments of R6 000 at the end of every 3 months.
Since the first repayment will be made 3 months from now, we can consider that the initial loan repayment is made at time t = 0. This means that we need to calculate the value of t when the total amount repaid is equal to the initial amount borrowed.
Using the formula for compound interest: A = P(1 + r/n)^(nt), We can calculate the quarterly interest rate:r = (5.25/100)/4 = 0.013125We also know that the quarterly repayment amount is R6 000, so the amount borrowed minus the first repayment is the present value of the loan: P = R200 000 - R6 000 = R194 000
We can now substitute these values into the formula and solve for t: R194 000(1 + 0.013125/4)^(4t) = R200 000(1 + 0.013125/4)^(4t-1) + R6 000(1 + 0.013125/4)^(4t-2) + R6 000(1 + 0.013125/4)^(4t-3) + R6 000(1 + 0.013125/4)^(4t)
Rearranging the terms gives us: R194 000(1 + 0.013125/4)^(4t) - R6 000(1 + 0.013125/4)^(4t-1) - R6 000(1 + 0.013125/4)^(4t-2) - R6 000(1 + 0.013125/4)^(4t-3) - R200 000(1 + 0.013125/4)^(4t) = 0
Using trial and error, we can solve this equation to find that t = 5.22 years (rounded to 2 decimal places). Therefore, it will take Andrew approximately 5.22 years to settle the loan.
For more questions on: compound interest
https://brainly.com/question/31474686
#SPJ8
State the equation of the graphed function.

Answers
The equation of the graphed function is given as follows:
f(x) = x³ + 2x² - 5x - 6.
How to obtain the equation of the function?
The equation of the function is obtained considering the Factor Theorem, as a product of the linear factors of the function.
From the graph, the zeros of the function are:
x = -3.x = -1.x = 2.Hence the function is:
f(x) = a(x + 3)(x + 1)(x - 2).
In which a is the leading coefficient.
Expanding the product, we have that:
f(x) = a(x² + 4x + 3)(x - 2)
f(x) = a(x³ + 2x² - 5x - 6).
When x = 0, y = -6, hence the leading coefficient a is obtained as follows:
-6a = -6
a = 1.
Hence the function is:
f(x) = x³ + 2x² - 5x - 6.
More can be learned about functions at https://brainly.com/question/24808124
#SPJ1
The perimeter of a college basketball court is 96 meters and the length is 14 meters more than the width. What are the dimensions
Answers
Answer:
length = 32m, width= 16m
Step-by-step explanation:
l=2w
2(2w+w)=96
2(3w)=96
6w=96,w= 96/6 = 16m
l=2w=2x16=32m
Answer:
Width is 17, and length is 31
Step-by-step explanation:
The perimeter is all the sides added up.
96 is our perimeter.
We can call the width x, so that the length would be x+14
We have two widths and two lengths, and we can make that into an equation.
2(x)+2(x+14)=96
4x+28=96
4x=68
x=17
So now, we know that the width is 17.
Add 14 to that, and you will get 32.
You can double check this.
17+17=34
31+31=62
34+62=96.
Hope it helped.
In a recent election, 63% of all registered voters participated in voting. In a survey of 275 retired voters, 162 participated in voting. Which is higher, the population proportion who participated or the sample proportion from this survey?
Answers
The population proportion who participated in voting (63%) is higher than the sample proportion from this survey (58.91%).
To determine whether the population proportion who participated in voting or the sample proportion from the survey is higher, we need to compare the percentages.
The population proportion who participated in voting is given as 63% of all registered voters.
This means that out of every 100 registered voters, 63 participated in voting.
In the survey of retired voters, 162 out of 275 participants voted. To calculate the sample proportion, we divide the number of retired voters who participated (162) by the total number of retired voters in the sample (275) and multiply by 100 to get a percentage.
Sample proportion = (162 / 275) \(\times\) 100 ≈ 58.91%, .
Comparing the population proportion (63%) with the sample proportion (58.91%), we can see that the population proportion who participated in voting (63%) is higher than the sample proportion from this survey (58.91%).
Therefore, based on the given data, the population proportion who participated in voting is higher than the sample proportion from this survey.
It's important to note that the sample proportion is an estimate based on the surveyed retired voters and may not perfectly represent the entire population of registered voters.
For similar question on population proportion.
https://brainly.com/question/29516589
#SPJ8
Find the mode of the data. 8,4,5,3,4,5,3,7,6
Answers
Answer:
3,4,5
Step-by-step explanation:
appear mutiple times
Mode= 4, 5, 3
this is mode for the data because To find the mode, or modal value,it is best to put the numbers in order. Then count how many of each number. A number that appears most often is the mode...hope this helps
Uranus has three moons less than Saturn. Together they have 33 moons. How many moons does Saturn have? write an algebra equation to solve the problem
Answers
Answer:
Saturn has 18 moons.
Step-by-step explanation:
Let s = the number of moons of Saturn.
Then s - 3 is the number of moons of Jupiter.
s + s - 3 = 33
2s - 3 = 33
2s = 36
s = 18
Saturn has 18 moons.
what is the equation of y=x^3 with the given transformations
Answers
Each transformation affects the shape and position of the graph. It is important to carefully consider the order of the transformations and their impact on the equation.
1. Horizontal Shift (c):
If there is a horizontal shift, the equation becomes y = (x - c)^3.
For example, if there is a shift of 2 units to the right, the equation would be y = (x - 2)^3.
2. Vertical Shift (d):
If there is a vertical shift, the equation becomes y = x^3 + d.
For example, if there is a shift of 3 units upwards, the equation would be y = x^3 + 3.
3. Vertical Stretch (a):
If there is a vertical stretch or compression, the equation becomes y = a * x^3.
For example, if there is a vertical stretch by a factor of 2, the equation would be y = 2 * x^3.
4. Reflection (along the x-axis):
If there is a reflection along the x-axis, the equation becomes y = -x^3.
This flips the graph of the original function upside down.
5. Reflection (along the y-axis):
If there is a reflection along the y-axis, the equation becomes y = (-x)^3.
This mirrors the graph of the original function.
6. Combined Transformations:
If there are multiple transformations, we can apply them in the order they are given. For example, if there is a vertical stretch by a factor of 2 and a horizontal shift of 3 units to the right, the equation would be y = 2 * (x - 3)^3.
Remember, each transformation affects the shape and position of the graph. It is important to carefully consider the order of the transformations and their impact on the equation.
To know more about equation here:
brainly.com/question/29292690
#SPJ11
calculating the one-sample z-test serves to give you
Answers
Calculating the one-sample z-test gives you a z-score, which is a standardized measure of how far the sample mean is from the population mean.
How to explain the informationThe z-score can be used to determine whether the sample mean is significantly different from the population mean. A z-score of 1.96 or greater is considered to be statistically significant at the .05 level, and a z-score of 2.58 or greater is considered to be statistically significant at the .01 level.
The one-sample z-test is a statistical test used to determine if a sample mean significantly differs from a known population mean when the population standard deviation is known. The test provides a z-score, which can be used to calculate the probability (p-value) associated with the observed sample mean.
Learn more about sample on
https://brainly.com/question/24466382
#SPJ1
Calculating the one-sample z-test gives you a ......
What is the slope of the line that passes through the points (2, -3) and (1, -2)? Write your answer in simplest form.
Answers
Given:-
\( \textsf{( 2 , -3 ) -- point [ i ]}\)\( \: \)
\( \textsf{( 1 , -2 ) -- point [ ii ]}\)\( \: \)
To find:-
\( \textsf{slop of the line = ?}\)\( \: \)
By using formula:-
\( {\color{hotpink}\bigstar} {\boxed{\sf {\green{ slope : m = \: \frac{y_2 - y_1}{x_2 - x_1} }}}}\)
Solution:-
\( \sf \: m = \frac{y_2 - y_1}{x_2 - x_1} \)
\( \: \)
where ,
\( \green \star \underline{ \sf \: 2 = x_1 , -3 = y_1\: }\)\( \: \)
\( \green \star{ \underline{ \sf{ \:1 = x_2 , -2 = y_2 \: }}}\)\( \: \)
\( \sf \: m = \frac{( -2 ) - ( -3 ) }{1 - 2} \)
\( \: \)
\( \sf \: m = \frac{ - 2 + 3}{ \: 1 - 2} \)
\( \: \)
\( \sf \: m = \cancel \frac{1}{ - 1} \)
\( \: \)
\( \underline{\boxed{ \sf{ \blue{ \: m = -1 \: }}}}\)
\( \: \)
━━━━━━━━━━━━━━━━━━━━━━━
hope it helps:)
8(10-k)-2k=0 just need help solving
Answers
Answer:
k=8
Step-by-step explanation:
8(10-k)-2k=0
80-8k-2k=0
80-10k=0
-10k=-80
-80/-10
k=8
Answer:
The answer to this problem is k=8
Urgent! Find the length of the tangent segment AC given circle B below
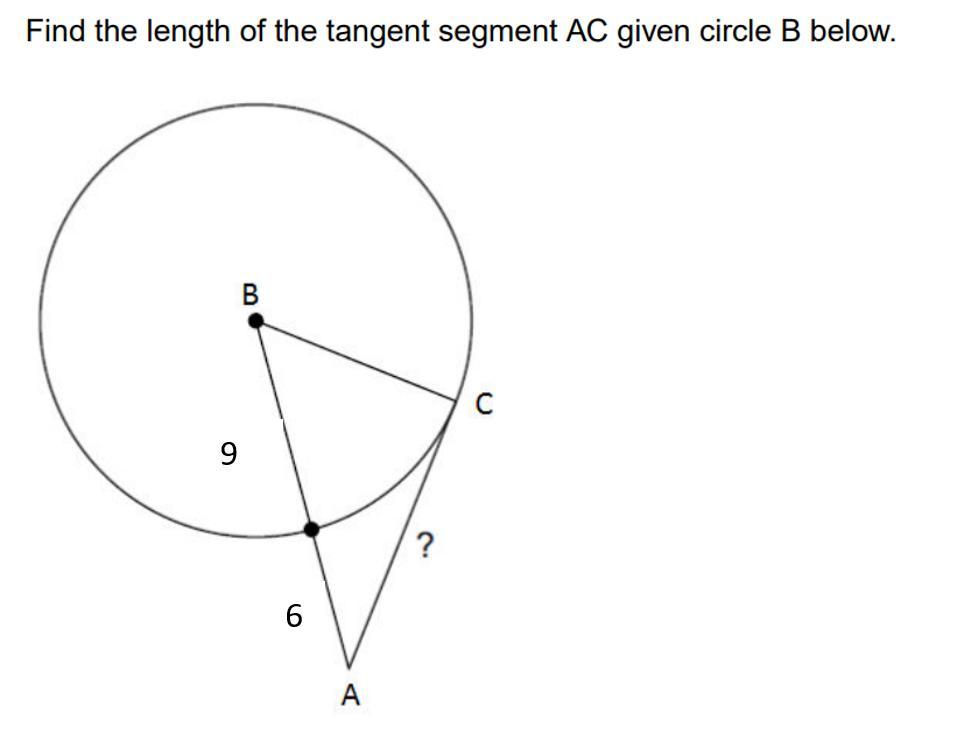
Answers
Answer:
AC ≈ 12
Step-by-step explanation:
the angle between the tangent AC and the radius BC is 90°
then Δ ABC is right
note that BC = 9 ( radius of circle )
using Pythagoras' identity in the right triangle
AC² + BC² = AB²
AC² + 9² = (9 + 6)² = 15²
AC² + 81 = 225 ( subtract 81 from both sides )
AC² = 144 ( take square root of both sides )
AC = \(\sqrt{144}\) = 12