The form of malnutrition in which children appear to be of normal weight but are shorter than they should be for their age is termed
Answers
Stunting is the term used to describe a form of malnutrition in which children have a low height-for-age ratio. It is characterized by children appearing to have normal weight but being shorter than they should be for their age.
Stunting is a result of chronic malnutrition, typically experienced during the first 1,000 days of a child's life, from conception to the age of two.
Stunting is a prevalent issue in many developing countries, where access to nutritious food, clean water, and proper healthcare may be limited. It is primarily caused by a lack of adequate nutrition, particularly a deficiency in essential nutrients such as protein, vitamins, and minerals. Additionally, factors like poor sanitation, recurrent infections, and inadequate maternal and child care contribute to stunting.
The consequences of stunting are significant and long-lasting. It affects not only physical growth but also cognitive development, immune function, and overall well-being. Stunted children are at a higher risk of developmental delays, reduced learning capacity, and increased susceptibility to diseases. The impact of stunting can extend into adulthood, leading to reduced productivity and economic potential.
Addressing stunting requires comprehensive interventions that focus on improving maternal and child nutrition, access to clean water and sanitation, and healthcare services. Promoting exclusive breastfeeding, providing nutrient-rich foods, and implementing public health programs are essential in combating stunting and ensuring optimal growth and development for children.
To learn more about ratio, click here: brainly.com/question/24643676
#SPJ11
Related Questions
Assuming that 100 shares were bought in each company, which pair would give you the
greatest return on an investment made in year 1 and cashed in year 5?
Answers
In year one and five, we see that Peer Com and CDX Groul produced the greatest return on investment.
How to interpret Graphs?From the graph attached, we see that it represents the year in which the greatest return on investment was made on the x-axis while the y-axis shows the value of 100 shares in dollars.
Now, in year 1, the pair that would give the greatest return on investment are; Peer Com and CDX Groul
Similarly, in year five we see that Peer Com and CDX Groul produce the greatest return on investment.
Read more about Graphs at; https://brainly.com/question/4025726
#SPJ1

a homeowner has budgeted $10,000 for some home remodeling. a contractor has told him the labor and the cost of materials will be about the same amount. the homeowner wants to have about $3,000 left over for furnishings. how much will the homeowner be able to spend on labor and on materials?
Answers
Answer:
$3,500 labor and $3,500 materials
Step-by-step explanation:
furnishings + labor + materials = 10,000
furnishings = 3000
3000 + labor + materials = 10,000
labor = materials
3000 + labor + labor = 10,000
2(labor) = 7,000
labor = 7,000/2
labor = 3,500
labor = materials = 3,500
What is the parent function for y = |x - 41+7?
Answers
Explanation :
0=x-34
-x= -34
Answer = x=34
Y=x-41+7
Y=x-48
X=48
hi la amigos y amigas what is 26 divded by 2 plus 5?
Answers

Find m so that the equation msin²x+cos²x=m-1 has a solution on the interval (0;π/4)
Answers
msin²x+cos²x=m-1
since the interval are 0 and π/4
Therefore
msin²(0)+cos²(0)=m-1
m(0)+1=m-1
1=m-1
m=2
use π/4 now
msin²(π/4)+cos²(π/4)=m-1
m(1/2)+(1/2)=m-1
m+1=2(m-1)
m+1=2m-2
-m=-3
m=3
Therefore
m=2 or 3
Your friend is celebrating her 25 th birthday today and wants to start saving for her anticipated retirement at age 65 . She wants to be able to withdraw $250,000 from her saving account on each birthday for 20 years following her retirement; the first withdrawal will be on her 66th birthday. Your friend intends to invest her money in a retirement account, which earns 8 percent return per year. She wants to make an equal annual deposit on each birthday into the account for her retirement fund. Assume that the annual return on the retirement account is 8 percent before retirement and 5 percent after retirement. If she starts making these deposits on her 26 th birthday and continue to make deposits until she is 65 (the last deposit will be on her 65 th birthday and the total number of annual deposits is 40), what amount must she deposit annually to be able to make the desired withdrawals at retirement? (Hint: One way to solve for this problem is to first find the value on your friend's 65 th birthday of the $250,000 withdrawal per year for 20 years after her retirement using the annual return after retirement and then find the equal annual deposit that she needs to make from her 26th birthday to 65 th birthday using the annual return before retirement.) Ignore taxes and transaction costs for the problem.
Answers
The correct answer is your friend needs to deposit approximately $13,334.45 annually from her 26th birthday to her 65th birthday to be able to make the desired withdrawals at retirement.
To determine the annual deposit your friend needs to make for her retirement fund, we'll calculate the present value of the desired withdrawals during retirement and then solve for the equal annual deposit.
Step 1: Calculate the present value of the withdrawals during retirement
Using the formula for the present value of an annuity, we'll calculate the present value of the $250,000 withdrawals per year for 20 years after retirement.
\(PV = CF * [1 - (1 + r)^(-n)] / r\)
Where:
PV = Present value
CF = Cash flow per period ($250,000)
r = Rate of return after retirement (5%)
n = Number of periods (20)
Plugging in the values, we get:
PV = $250,000 * \([1 - (1 + 0.05)^(-20)] / 0.05\)
PV ≈ $2,791,209.96
Step 2: Calculate the equal annual deposit before retirement
Using the formula for the future value of an ordinary annuity, we'll calculate the equal annual deposit your friend needs to make from her 26th birthday to her 65th birthday.
\(FV = P * [(1 + r)^n - 1] / r\)
Where:
FV = Future value (PV calculated in Step 1)
P = Payment (annual deposit)
r = Rate of return before retirement (8%)
n = Number of periods (40)
Plugging in the values, we get:
$2,791,209.96 = \(P * [(1 + 0.08)^40 - 1] / 0.08\)
Now, we solve for P:P ≈ $13,334.45
Therefore, your friend needs to deposit approximately $13,334.45 annually from her 26th birthday to her 65th birthday to be able to make the desired withdrawals at retirement.
Learn more about compound interest here:
https://brainly.com/question/24274034
#SPJ11
estimate the x-coordinates at which the relative maxima and minima occur for the function f(x)=4x3+11x2-5
Answers
The x coordinate of the relative minima and maxima of the function
f(x) = 4x^3 + 11x^2 - 5 is
at x = 0 minimaat x = -11/6 maximaWhat is relative maxima and relative minima?The relative minima and relative maxima are point on a graph of curves that gives the minimum and maximum points.
How to calculate the relative minima and maxima
Data gotten from the equation include:
f(x) = 4x^3 + 11x^2 - 5
To get the relative minima and the relative maxima we differentiate two times and watch the sign
f(x) = 4x^3 + 11x^2 - 5 x =
f'(x) = 12x^2 + 22x
equate the derivative to zero and solve for x
0 = 12x^2 + 22x
0 = 2x(6x + 11 )
x = 0 OR x = -11/6
f''(x) = 24x + 22
at x = 0
f''(x) = 22 (minimum)
at x = -11/6
f''(x) = -22 (maximum)
Learn more on relative minima and maxima: https://brainly.com/question/9839310
#SPJ1
The correlation in error terms that arises when the error terms at successive points in time are related is termed _____. a. autocorrelation b. leverage c. multicorrelation d. parallel correlation
Answers
The correlation in error terms that arises when the error terms at successive points in time are related is termed autocorrelation
The correct answer is an option (a).
Correlation is the mutual connection between two or more variables. These variables can be dependent or independent but there should be random variables.
Autocorrelation is the degree of correlation between the values of the same variables across different data.
Instead of correlation between two different variables, the correlation is between two values of the same variable at times i and i + k.
It is used for the following two purposes:
- To detect non-randomness in data.
- To identify an appropriate time series model if the data are not random.
Therefore, The correlation in error terms that arises when the error terms at successive points in time are related is termed autocorrelation
The correct answer is an option (a).
Learn more about autocorrelation here:
https://brainly.com/question/14134127
#SPJ4
ty
What is the equation of the line that is parallel to the
given line and passes through the point (-2, 2)?
5
4
2
1
O y = -x+4
O y=-x+ 13
O y = -5x + 4
O y = -5x + 12
-2
5
(0, -3)
(-5, 4)
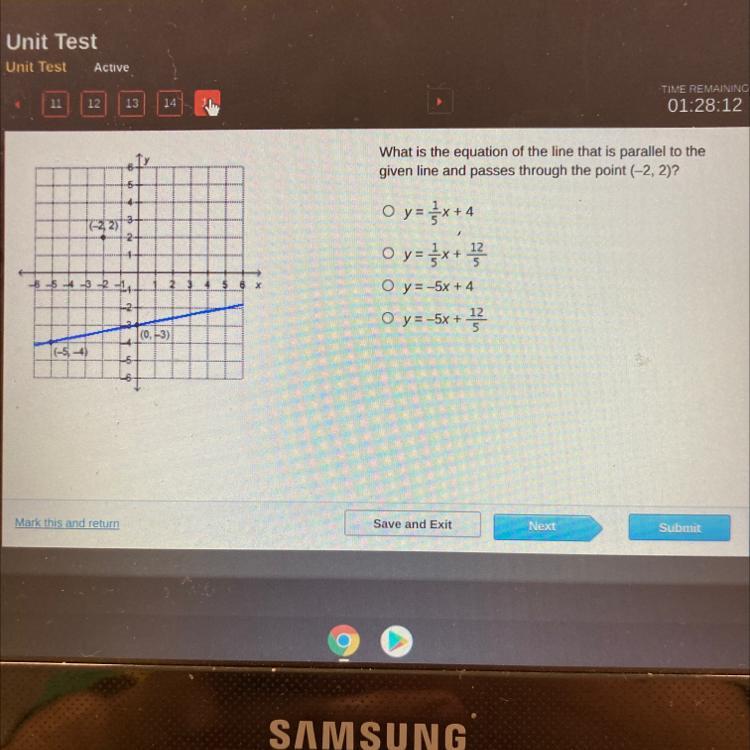
Answers
Answer:
O y=_5x+4 it is equation the line that is parallel
The equation of line passes through the point (-2, 2) will be;
⇒ y = 1/5x - 12/5
What is Equation of line?The equation of line in point-slope form passing through the points
(x₁ , y₁) and (x₂, y₂) with slope m is defined as;
⇒ y - y₁ = m (x - x₁)
Where, m = (y₂ - y₁) / (x₂ - x₁)
Given that;
Two points on the line are (- 5, -4) and (0, -3).
Now,
Since, The equation of line passes through the points (- 5, -4) and (0, -3).
So, We need to find the slope of the line.
Hence, Slope of the line is,
m = (y₂ - y₁) / (x₂ - x₁)
m = (- 3 - (-4)) / (0 - (-5))
m = 1 / 5
Hence, The slope of parallel line = 1/5
Thus, The equation of line with slope 1/5 and passes through the point (-2, 2) is,
⇒ y - (-2) = 1/5 (x - 2)
⇒ y + 2 = 1/5x - 2/5
⇒ y = 1/5x - 2/5 - 2
⇒ y = 1/5x - 12/5
Therefore, The equation of line passes through the point (-2, 2) will be;
⇒ y = 1/5x - 12/5
Learn more about the equation of line visit:
https://brainly.com/question/18831322
#SPJ7
Griffin ordered a pair of sneakers online. He had a $19 credit that he applied toward the purchase, and
then he used a credit card to pay for the rest of the cost. If the shoes cost $78, how much did Griffin
charge to his credit card when he bought the sneakers?
A. $40
B. $116
C. $97
D. $59
Answers
Answer:
59
Step-by-step explanation:
78-19=59
Answer: D, 59
Step-by-step explanation:
So we know that the total cost is 78 dollars. If we take 78 and minus 19, it leaves us with 59. Pls brainliest
A store manager kept track of the number of newspapers sold each week over a seven-week period. The results are shown below. \( 87,87,215,154,288,235,231 \) Find the median number of newspapers sold.
Answers
The median number of newspapers sold over seven weeks is 223.
The median is the middle score for a data set arranged in order of magnitude. The median is less affected by outliers and skewed data.
The formula for the median is as follows:
Find the median number of newspapers sold. (87, 87, 215, 154, 288, 235, 231)
We'll first arrange the data in ascending order.87, 87, 154, 215, 231, 235, 288
The median is the middle term or the average of the middle two terms. The middle two terms are 215 and 231.
Median = (215 + 231)/2
= 446/2
= 223
In statistics, the median measures the central tendency of a set of data. The median of a set of data is the middle score of that set. The value separates the upper 50% from the lower 50%.
Hence, the median number of newspapers sold over seven weeks is 223.
To know more about the median, visit:
brainly.com/question/300591
#SPJ11
identify the least integer such that () is () for each of these functions. a) ()=35 2 2 4
Answers
To find the least integer for which the given function satisfies the condition, we need to identify the value of the variable that makes the function equal to 35.
The function provided is ()=35 2 2 4. Unfortunately, the expression seems to be incomplete or missing some information. To accurately determine the least integer, we would need additional details about the function, such as the variable involved and its equation or formula.
Without a clear understanding of the function's structure and missing information, it is not possible to generate a specific answer. Please provide the complete equation or formula for the function, including the variable and any additional parameters or constraints, so that I can assist you further in finding the least integer that satisfies the condition.
To learn more about function click here, brainly.com/question/31062578
#SPJ11
If f(x) = 5x + 40, what is f(x) when x = -5? og O 8 O 7 O 15
Answers
Answer:
15.
Step-by-step explanation:
5 * - 5 + 40 = 15
Answer:
15
Step-by-step explanation:
f(x) = 5x + 40
Let x = -5
f(-5) = 5(-5) + 40
Multiply
= -25+40
Add
= 15
TRUE/FALSE. if new data will be collected (i.e., primary data collection), the researcher can easily recruit an adequate number of participants.
Answers
If new data will be collected (i.e., primary data collection), the researcher can easily recruit an adequate number of participants is false.
What is statistics?Statistics is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data.
Given,
We need to check whether if new data will be collected (i.e., primary data collection), the researcher can easily recruit an adequate number of participants is true or false.
The given statement is false because Primary data collection is a process of collecting original data, directly from the source.
Hence, if new data will be collected (i.e., primary data collection), the researcher can easily recruit an adequate number of participants is false.
To learn more on Statistics click:
https://brainly.com/question/29342780
#SPJ1
Which of the following could not be the graph of a function of X?

Answers
Answer:
D
Step-by-step explanation:
A function cannot have to values of y for a same x, and he only which have it is the graph D
a random experiment was conducted to see if a newly formulated drug produced a different effect on the mean time to recovery than that achieved using the standard drug. it is known that the mean time to recovery for the standard drug is 26 days. following an extensive random experiment involving 65 patients, the data gathered were used to construct a 95% confidence interval estimate for the mean recovery time (in days) for patients on the new drug. the 95% confidence interval was found to be (24.6, 27.8). what conclusion can be reached in this case concerning the new drug relative to the standard drug
Answers
Based on the given information, we conducted a random experiment to compare the mean time to recovery between a newly formulated drug and the standard drug. The mean time to recovery for the standard drug is known to be 26 days.
After an extensive random experiment involving 65 patients, we constructed a 95% confidence interval estimate for the mean recovery time for patients on the new drug, which was found to be (24.6, 27.8) days.
Based on this information, we can conclude that the mean recovery time for patients on the new drug is significantly different from the mean recovery time for patients on the standard drug. Since the confidence interval for the new drug does not include the mean recovery time of the standard drug (26 days), it suggests that the new drug produces a different effect on the mean time to recovery compared to the standard drug.
Let's learn more about interval:
https://brainly.com/question/17097944
#SPJ11
The position of a particle as it moves horizontally is described by the given equations. If s is the displacement in metres and t is the time in seconds find the absolute maximum and absolute minimum displacements. (a) s = 2 sin t + sin 2t, -π ≤ t ≤ π (b) f(t) = sin^2 t - 2 cos^2 t, -π ≤ t ≤ π
Answers
The absolute maximum displacement is 2, and the absolute minimum displacement is -2.
What is absolute maximum displacement?
The absolute maximum displacement refers to the maximum value attained by the displacement function over a given interval. the absolute maximum displacement represents the highest value of the displacement function s(t) or f(t) over the specified interval. It indicates the farthest distance the particle reaches from its initial position during the given time period.
What is absolute minimum displacement?
The absolute minimum displacement refers to the minimum value attained by the displacement function over a given interval. the absolute minimum displacement represents the lowest value of the displacement function s(t) or f(t) over the specified interval. It indicates the closest distance the particle reaches to its initial position during the given time period.
To find the absolute maximum and minimum displacements, we need to find the critical points of the given equations and evaluate the function at those points. Let's solve each part separately:
(a) s = 2 sin t + sin 2t, -π ≤ t ≤ π
To find the critical points, we need to find where the derivative of s with respect to t equals zero. Let's differentiate s with respect to t:
ds/dt = 2 cos t + 2 cos 2t
Setting ds/dt equal to zero:
2 cos t + 2 cos 2t = 0
Divide both sides by 2:
cos t + cos 2t = 0
Using the trigonometric identity cos 2t = 2 cos^2 t - 1, we can rewrite the equation:
cos t + 2 cos² t - 1 = 0
Rearranging the terms:
2 cos² t + cos t - 1 = 0
Now, let's solve this quadratic equation. We can factor it:
(2 cos t - 1)(cos t + 1) = 0
Setting each factor equal to zero:
2 cos t - 1 = 0 or cos t + 1 = 0
Solving for cos t in the first equation:
2 cos t = 1
cos t = 1/2
t = π/3, 5π/3
Solving for cos t in the second equation:
cos t = -1
t = π
Now we have the critical points t = π/3, π, and 5π/3. We also need to evaluate the function at the endpoints of the given interval, t = -π and t = π.
Let's calculate the values of s at each of these points:
s(-π) = 2 sin(-π) + sin(2(-π)) = 0
s(π/3) = 2 sin(π/3) + sin(2(π/3)) = 3√3/2
s(π) = 2 sin(π) + sin(2π) = 0
s(5π/3) = 2 sin(5π/3) + sin(2(5π/3)) = -3√3/2
s(π) = 2 sin(π) + sin(2π) = 0
So, we have the following values for s:
s(-π) = 0
s(π/3) = 3√3/2
s(π) = 0
s(5π/3) = -3√3/2
s(π) = 0
The absolute maximum displacement is 3√3/2, and the absolute minimum displacement is -3√3/2.
(b) f(t) = sin² t - 2 cos² t, -π ≤ t ≤ π
Let's find the critical points of f(t) by finding where the derivative of f with respect to t equals zero. We'll differentiate f(t) with respect to t:
df/dt = 2 sin t cos t + 4 cos t sin t
Setting df/dt equal to zero:
2 sin t cos t + 4 cos t sin t = 0
Simplifying:
6 sin t cos t = 0
sin t cos t = 0
This equation is satisfied when sin t = 0 or cos t = 0.
When sin t = 0, we have t = 0, π,
To find the absolute maximum and minimum displacements, we need to evaluate the function at critical points and endpoints. Let's proceed with the calculations:
(a) s = 2 sin t + sin 2t, -π ≤ t ≤ π
We found the critical points earlier: t = π/3, π, and 5π/3. We also need to evaluate the function at the endpoints of the given interval, t = -π and t = π.
Let's calculate the values of s at each of these points:
s(-π) = 2 sin(-π) + sin(2(-π)) = 0
s(π/3) = 2 sin(π/3) + sin(2(π/3)) = 3√3/2
s(π) = 2 sin(π) + sin(2π) = 0
s(5π/3) = 2 sin(5π/3) + sin(2(5π/3)) = -3√3/2
s(π) = 2 sin(π) + sin(2π) = 0
So, we have the following values for s:
s(-π) = 0
s(π/3) = 3√3/2
s(π) = 0
s(5π/3) = -3√3/2
s(π) = 0
The absolute maximum displacement is 3√3/2, and the absolute minimum displacement is -3√3/2.
(b) f(t) = sin² t - 2 cos² t, -π ≤ t ≤ π
To find the absolute maximum and minimum, we need to evaluate the function at the critical points and endpoints.
Critical points: sin t = 0 or cos t = 0
When sin t = 0, we have t = 0, π, and -π.
Let's calculate the values of f at each of these points:
f(0) = sin²(0) - 2 cos²(0) = 0 - 2(1) = -2
f(π) = sin²(π) - 2 cos²(π) = 0 - 2(-1) = 2
f(-π) = sin²(-π) - 2 cos²(-π) = 0 - 2(-1) = 2
Now let's evaluate the function at the endpoints:
f(-π) = sin²(-π) - 2 cos²(-π) = 0 - 2(1) = -2
f(π) = sin²(π) - 2 cos² mnbdmbr(π) = 0 - 2(-1) = 2
So, we have the following values for f:
f(-π) = -2
f(0) = -2
f(π) = 2
Therefore, absolute maximum displacement is 2, and the absolute minimum displacement is -2.
To learn more about Motion in one dimension follow the given link:
https://brainly.com/question/1772276
#SPJ4
negative sixteen plus the quotient of a number and -4 is -3
Answers
Answer:
The number is 76
Step-by-step explanation:
2х + 3x +3+ 4х2 +10 +x
HELPP ASAP NEED ANSWER AND SHOW WORKK

Answers
Answer:
4x² + 6x + 13
Step-by-step explanation:
Add like terms:
2x + 3x + x + 4x²+3
6x + 4x² + 3
Rearrange to put x² at the front:
4x² + 6x + 13
If this isn't the answer you were looking for, let me know.
Hope this helps!
Someone pls help me!!! Will give brainliest! A survey of 1000 students found that 41% of the surveyed students were freshmen, 31% were juniors, and 67% lived on the college campus. (A) If 260 of the surveyed students were freshmen living on the college cam- pus, then how many surveyed students were either freshmen or living on campus? (B) Suppose from a previous survey you know that of interviewed juniors, only 23% live on campus. What is the probability a surveyed student is a junior or someone that lives on campus?
Answers
Answer:
(A) 560 students
(B) P = 0.41
Step-by-step explanation:
(Please check the attached picture for more details)
As given, a survey of 1000 students found that:
41% of the surveyed students were freshmen
=> 1000 x 41/100 = 410 surveyed students were freshmen
31% were juniors
=> 1000 x 31/100 = 310 surveyed students were junior
67% of surveyed students lived on the college campus
=> 1000 x 67/100 = 670 surveyed students lived on the campus
(A) 260 of the surveyed students were freshmen living on the campus
=> A = 410 - 260 = 150 surveyed students were freshmen NOT living on the campus
=> B = 670 - 260 = 410 surveyed students were not freshmen living on the campus
=> The number of surveyed students who were either freshmen or living on the campus:
N = A + B = 150 + 410 = 560
(B) From a previous survey you know that of interviewed juniors, only 23% live on campus (we don't really need this)
=>The probability a surveyed student is a junior or someone that lives on campus: P = (670 - 260)/1000 = 0.41
I hope this helps!

3. Find the area of the trapezoid.
(1 point)
14.5 cm
1
8 cm
19.5 cm
68 cm
O 136 cm
214 cm
268 cm
4. The radius of
Answers
ANSWER ASAP!! DUE SOON! ONLY ANSWER IF YOU ARE CORRECT, I CANNOT GET THIS WRONG!!!

Answers
Answer:63 degrees
Step-by-step explanation:
90-27=63
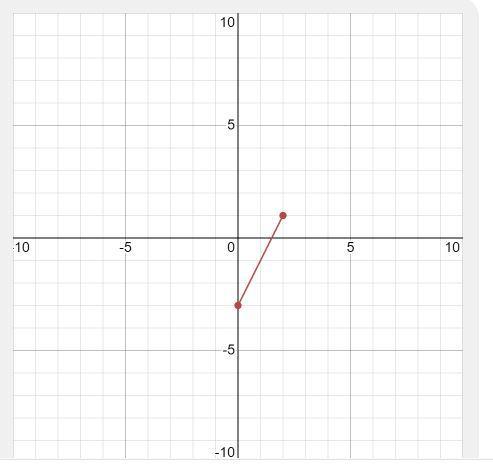
Plot the points (0,-3) and (2, 1) and find slope
.
Answers
Answer:
The slope is M= 2
Step-by-step explanation:
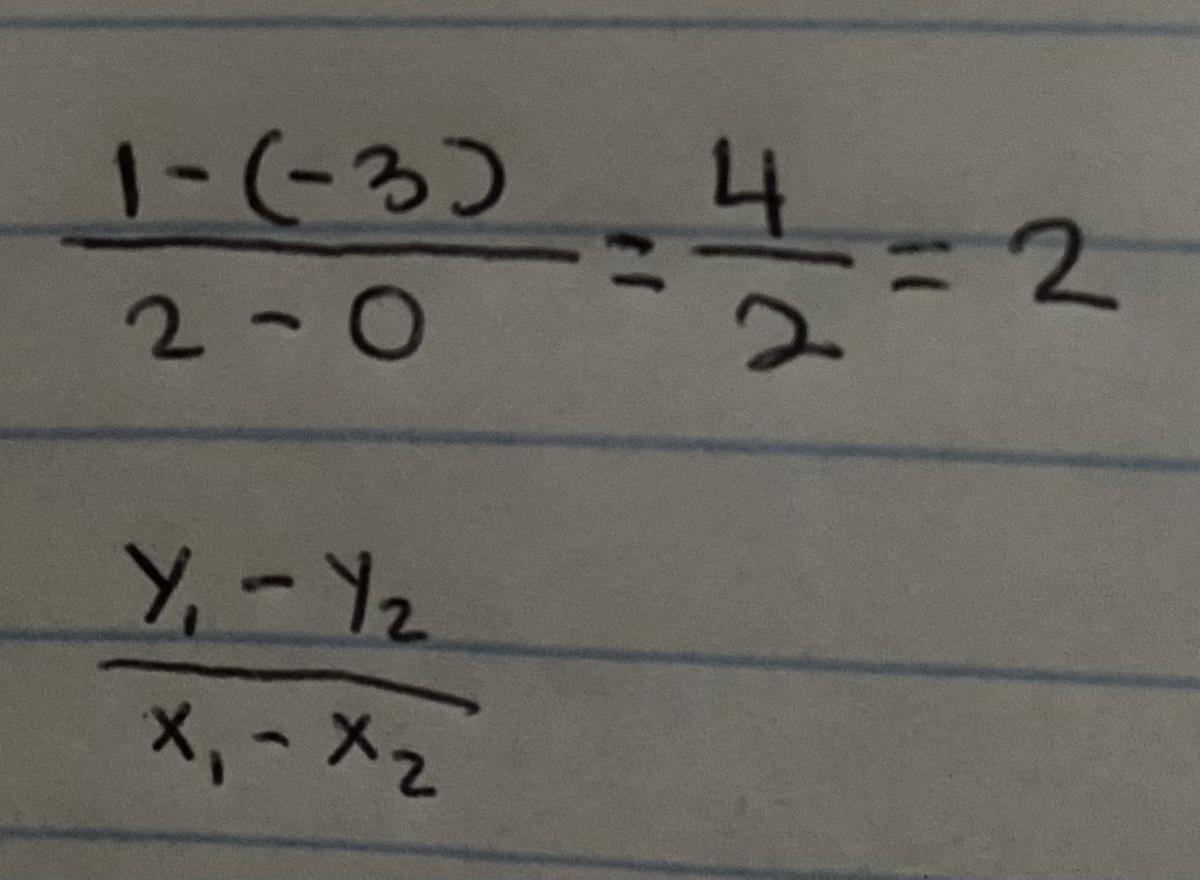
at what point do the curves r1(t) = t, 4 − t, 63 t2 and r2(s) = 9 − s, s − 5, s2 intersect? (x, y, z) =
Answers
The curves r1(t) = (t, 4 - t, 63t^2) and r2(s) = (9 - s, s - 5, s^2) intersect at the point (x, y, z), which can be determined by solving the system of equations derived from the coordinates of the curves.
To find the intersection point of the curves r1(t) and r2(s), we need to solve the system of equations formed by equating the corresponding components of the two curves. Let's equate the x-components, y-components, and z-components separately.
From r1(t), we have x = t, y = 4 - t, and z = 63t^2.
From r2(s), we have x = 9 - s, y = s - 5, and z = s^2.
Equating the x-components: t = 9 - s
Equating the y-components: 4 - t = s - 5
Equating the z-components: 63t^2 = s^2
We can solve this system of equations to find the values of t and s that satisfy all three equations. Once we have t and s, we can substitute these values back into the expressions for x, y, and z to obtain the coordinates of the intersection point (x, y, z).
Solving the first equation, we get t = 9 - s. Substituting this into the second equation, we have 4 - (9 - s) = s - 5, which simplifies to -5s = -16. Solving for s, we find s = 16/5. Substituting this value back into t = 9 - s, we get t = 9 - (16/5) = 19/5.
Now, substituting t = 19/5 and s = 16/5 into the expressions for x, y, and z, we find:
x = 19/5, y = -1/5, z = (63(19/5)^2).
Therefore, the curves r1(t) and r2(s) intersect at the point (19/5, -1/5, 7257/25) or approximately (3.8, -0.2, 290.28).
to learn more about system of equations, click: brainly.com/question/2237397
#SPJ11
What is 180 divided by 2
Answers
Answer:
90
Step-by-step explanation:
Do it on the calculator 180÷2
Someone please help me for a brainliest.

Answers
Answer:
a) 15 minutes
b) Input is temp, output is time.
Step-by-step explanation:
3a) After how many minutes is the temperature 35.
Find 35 on the second row, and see that it takes 15 minutes.
3b) For the inverse function, the input is the temperature, and the output the number of minutes.
Solve the differential equations 2xy(dy/dx)=1 y^2. y(2)=3
Answers
The solution to the given differential equation 2xy(dy/dx) = y², with the initial condition y(2) = 3, is y = (27 * e⁽ˣ⁻²⁾\()^{1/4}\).
To solve the given differential equation
2xy(dy/dx) = y²
We will use separation of variables and integrate to find the solution.
Start with the given equation
2xy(dy/dx) = y²
Divide both sides by y²:
(2x/y) dy = dx
Integrate both sides:
∫(2x/y) dy = ∫dx
Integrating the left side requires a substitution. Let u = y², then du = 2y dy:
∫(2x/u) du = ∫dx
2∫(x/u) du = ∫dx
2 ln|u| = x + C
Replacing u with y²:
2 ln|y²| = x + C
Using the properties of logarithms:
ln|y⁴| = x + C
Exponentiating both sides:
|y⁴| = \(e^{x + C}\)
Since the absolute value is taken, we can remove it and incorporate the constant of integration
y⁴ = \(e^{x + C}\)
Simplifying, let A = \(e^C:\)
y^4 = A * eˣ
Taking the fourth root of both sides:
y = (A * eˣ\()^{1/4}\)
Now we can incorporate the initial condition y(2) = 3
3 = (A * e²\()^{1/4}\)
Cubing both sides:
27 = A * e²
Solving for A:
A = 27 / e²
Finally, substituting A back into the solution
y = ((27 / e²) * eˣ\()^{1/4}\)
Simplifying further
y = (27 * e⁽ˣ⁻²⁾\()^{1/4}\)
Therefore, the solution to the given differential equation with the initial condition y(2) = 3 is
y = (27 * e⁽ˣ⁻²⁾\()^{1/4}\)
To know more about differential equation:
https://brainly.com/question/2273154
#SPJ4
the amplitude of a sector of πcm² of area and 1.5 cm of radius
Answers
The area of the sector is A = π cm² and amplitude is a = 0.75 cm
Given data ,
The area of a sector is given by the formula:
A = (1/2) x r² x θ
where r is the radius of the sector and θ is the central angle in radians.
On simplifying , we get
A = π cm²
r = 1.5 cm
Substituting these values into the formula, we get:
π = (1/2) x (1.5)² x θ
π = (3/4) x θ
Solving for θ, we get:
θ = (4/3) x π
The amplitude of the sector is half of the radius, so:
amplitude = (1/2) x 1.5 cm = 0.75 cm
Hence , the amplitude of the sector is 0.75 cm
To learn more about area of sector click :
https://brainly.com/question/28180776
#SPJ1
Relative to the sinusoidal axes (dotted lines) what is the equation of this sinusoid?

Answers
Step-by-step explanation:
We know that the function period is 3 so the b value is
\( \frac{2\pi}{b} = 3\)
\(b = \frac{2\pi}{3} \)
So our b is 2 pi/3.
The midline is -3 and the amplitude is 2.Since this function isn't symmetric about y axis, and looks symmetric about orgin, we trig function will be Sine so we have
\(2 \sin ( \frac{2\pi}{3}x ) - 3\)
The function passes through 0,-3 and our function on the graph passes through 1,-3 so we shift one unit to left.
\(2 \sin(\frac{2\pi}{3}(x + 1) ) - 3\)
a bag of chocolates is labeled to contain 0.384 pounds of chocolate. the actual weight of the chocolates is 0.3798 pounds. how much lighter is the actual weight?
Answers
The actual weight is 0.0042 pounds lighter than the labeled weight.
The actual weight of the chocolates is 0.3798 pounds, while the label on the bag states it should weigh 0.384 pounds. To determine how much lighter the actual weight is, we can calculate the difference between the two weights.
Subtracting the actual weight from the labeled weight, we get:
0.384 pounds - 0.3798 pounds = 0.0042 pounds.
Therefore, the actual weight is 0.0042 pounds lighter than the labeled weight.
It's important to note that this difference may seem small, but it can be significant depending on the context. Accuracy in labeling is crucial for various reasons, such as complying with regulations, providing precise information to consumers, and ensuring fair trade practices. Even minor discrepancies can impact trust and customer satisfaction.
For more information on actual weight visit: brainly.com/question/31170036
#SPJ11