The figure above shows the U.S. demand and supply curves for cherries. Suppose the world price of cherries is $2 per pound. How many pounds of cherries would be exported to the rest of the world?
Answers
If the world price of cherries is $2 per pound and assuming that the US is a price taker (i.e., it cannot affect the world price), then the US quantity demanded of cherries at that price point is represented by the US demand curve at the price of $2 per pound.
To determine the quantity of cherries that would be exported to the rest of the world, we need to find the difference between the quantity supplied in the US and the quantity demanded in the US at the given price of $2 per pound. This difference represents the amount of cherries that the US would be willing and able to sell to the rest of the world.
So, the quantity of cherries that would be exported to the rest of the world is equal to the difference between the quantity supplied and the quantity demanded in the US at the price of $2 per pound. If the quantity supplied at that price point is greater than the quantity demanded, then the US would export the excess to the rest of the world. If the quantity demanded is greater than the quantity supplied, then the US would import cherries from the rest of the world.
Without the actual values of the demand and supply curves and equilibrium quantity, it's not possible to provide an exact answer.
Related Questions
A right rectangular prism has the dimensions 4 by 6 by 3 feet. Enter the volume, in cubic feet, of the rectangular prism.
Answers
Explanation: volume= length x width x height
Therefore 4x6x3=72 cubic feet
We are given a jar full of thousands of red and blue marbles. We want to estimate the unknown proportion pof red marbles in the jar. To do this, we randomly draw 100 marbles and count reds: it so happens we drew 45 reds. Enter values in decimal form, rounded to four decimal places (or more).
We estimate the proportion of reds in the jar to be
Attach a give-or-take value to this estimate. (That is, estimate the standard error.)
For a 96% confidence interval, about how many standard errors should be added to and subtracted from the estimate?
Set up an approximate 96% confidence interval for the unknown proportion of reds in the jar.
Answers
Answer:
(0.3478, 0.5522)
Step-by-step explanation:
Given:
Total number of red marbles, x = 45
Total number of marbles, n = 100
Phat = x / n = 45 / 100 = 0.45
The confidence interval, C.I is given by :
Phat ± Zcritical * standard error
Phat ± Zcritical * √Phat(1 - Phat) / n
Zcritical at 96% = 2.0537
The standard error = √Phat(1 - Phat) / n
S.E = √(0.45 * 0.55) / 100 = 0.0497493
C.I = 0.45 ± (2.0537 * 0.0497493)
C.I = 0.45 ± 0.10217013741
C. I = (0.3478, 0.5522)
radius = 6.3mm.we are learning something about area of circle.
Answers
We have that the area of the circle with a radius of 6.3mm is the following:
\(A=\pi(6.3)^2\Rightarrow A=\pi(\frac{32969}{100})\Rightarrow A=39.69\pi\)The area is a
Find the measure of the arc or angle indicated.

Answers
The measure of the arc or angle is:
m∠NLM = 60 deg
How to find the measure of the arc or angle indicated?From the given figure, line LN is the diameter. Thus, the measure of arc LN is 180° (semicircle).
Thus, we can say:
arc NM + arc ML = 180°
(3x + 21) + (8x + 16) = 180°
11x + 37 = 180
11x = 180 - 37
11x = 143
x = 143/11
x = 13
arc NM = 8x + 16
put x = 13:
arc NM = 8(13) + 16 = 120°
Recall that:
The measure of inscribed angle is half the measure of its intercepted arc. That is:
m∠NLM = 1/2 * 120°
m∠NLM = 60°
Learn more about inscribed angles on:
brainly.com/question/30289513
#SPJ1
5c + d = c+ 4d find the ratio c:d
Answers
Answer:3c + 18d brainless pls
Step-by-step explanation:First, eliminate the parenthesis by multiplying each term within the parenthesis by the term outside the parenthesis:
3
(
5
c
+
4
d
)
+
6
(
d
−
2
c
)
⇒
(
3
⋅
5
c
)
+
(
3
⋅
4
d
)
+
(
6
⋅
d
)
−
(
6
⋅
2
c
)
⇒
15
c
+
12
d
+
6
d
−
12
c
Next, group like terms:
15
c
−
12
c
+
12
d
+
6
d
Now, combine like terms:
(
15
−
12
)
c
+
(
12
+
6
)
d
3
c
+
18
d,
Given:
\(\to 5c + d = c+ 4d\)
To find:
c:d=?
Solution:
\to 5c + d = c+ 4d
simulating the identical terms:
\(\to 5c -c = 4d-d\\\\\to 4c = 3d\\\\\to \frac{c}{d} = \frac{3}{4}\\\\\therefore\\\to c:d= 3:4\)
so, the ratio is 3:4
Learn more about the ratio:
brainly.com/question/4534527
What translation would map C onto A?
A. (x – 7, y + 3)
B. (x + 3, y – 7)
C. (x – 3, y + 7)
D. (x + 7, y – 3)

Answers
Answer:
A
Step-by-step explanation:
consider the coordinates of points C and A
C (4, - 1 ) and A (- 3, 2 )
4 → - 3 in the x- direction is - 7
- 1 → 2 in the y- direction is + 3
then the translation rule is
(x, y ) → (x - 7, y + 3 )
Need help I think it’s Ethan

Answers
Answer:
Ethan is the correct answer
What the meaning of statement this?

Answers
The statement Y = {u: (z X)uez) = U{z: zEX}=UX, means that the set Y is the union of all the sets z that are elements of X. In other words, Y is the set of all elements that are in at least one of the sets in X.
How to explain the statementThe statement can be broken down into two parts:
The first part, Y = {u: (z X)uez), says that Y is the set of all elements u such that u is an element of at least one set z that is an element of X.
The second part, U{z: zEX}=UX, says that the union of all the sets z that are elements of X is equal to the set UX.
The two parts of the statement can be combined to say that Y is the union of all the sets z that are elements of X.
Learn more about set on
https://brainly.com/question/2166579
#SPJ1
find the value of x. SIMPLEST RADICAL FORM

Answers
For given triangle, x is 4√5 using Pythagorean theorem.
What is Pythagorean Theorem?
Pythagoras Theorem (also known as Pythagorean Theorem) is a mathematical concept that explains the relationship between the sides of a right-angled triangle. The sides of a right triangle are also referred to as Pythagorean triples. This theorem's formula and proof are discussed with examples here.
The Pythagorean theorem is used to calculate the length of an unknown side and the angle of a triangle. We can deduce the base, perpendicular, and hypotenuse formulae from this theorem.
The Pythagoras Theorem formula is presented in the definition as:
Perpendicular² + Base² = Hypotenuse²
c² = a² + b²
Now,
Given that perpendicular =19
Hypotenuse=21
then Base²=21²-19² using Pythagoras theorem
Base=√441-361
=√80
=4√5
Hence,
x is 4√5
To know more about Pythagorean theorem visit the link
https://brainly.com/question/343682?referrer=searchResults
#SPJ1
Which of the following phrases in bold is an example of informal English?
After basketball practice Julie hit the books.
I really don't want to do my homework today.
Both Kelli and Rosa were late to the party.
Will ran down the street to catch the bus.
PLEASE HELP ME!!!!!!
Answers
Will ran down the street to catch the bus.
Hope this helps, thanks,
CoDBiarex
Answer:
After basketball practice Julie hit the books.
Step-by-step explanation:
Informal English often uses slang words that not everyone understands.
3 problems for 1 final answer. fairly easy 8th grade math.

Answers
When we evaluate the given expression, A/5 + √(B - C), the result obtained is 9 (option B)
How do i determine the value of A/5 + √(B - C)?
First, we shall determine the value of A. Details below:
A = Product of roots in x² - 11x + 30Value of A =?Quadratic equation is expressed as:
x² - (sum of root)x + product of root
Comparing the above with x² - 11x + 30, we have
x² - 11x + 30 = x² - (sumof root)x + product of root
Product of roots = 30
Thus,
A = 30
Next, we shall determine the value of B. details below:
f(x) = x² + 5Value of B = f(2) =?f(x) = x² + 5
f(2) = 2² + 5
f(2) = 9
Thus,
B = 9
Next, we shall determine the value of C. Details below:
(x² - 2x - 24) / (x + 4)Value of C = Remainder =?Let
x + 4 = 0
Thus,
x = -4
Substitute the value of x into x² - 2x - 24 to obtain the remainder as shown below:
Remainder = x² - 2x - 24
Remainder = (-4)² - 2(-4) - 24
Remainder = 0
Thus,
C = 0
Finally, we shall determine value of A/5 + √(B - C). Details below:
A = 30B = 9C = 0Value of A/5 + √(B - C) =?A/5 + √(B - C) = 30/5 + √(9 - 0)
A/5 + √(B - C) = 6 + √(9
A/5 + √(B - C) = 6 + 3
A/5 + √(B - C) = 9
Thus, the value of A/5 + √(B - C) is 9 (option B)
Learn more about algebraic expression:
https://brainly.com/question/12518138
#SPJ1
Six students write an exam. The average score obtained on the exam by the group of students is 71%. If the first two students each obtained a mark of 73%, while the next three students each obtained a mark of 68%, what was the mark obtained by the sixth student?
Answers
The first two students obtained a mark of 73%, which gives us a total of 73 + 73 = 146 marks.
The next three students obtained a mark of 68% each, which gives us a total of 68 + 68 + 68 = 204 marks.
The average score obtained by the group is 71%. Since there are six students, the total marks obtained by all six students would be 6 * 71 = 426 marks.
To find the mark obtained by the sixth student, we can subtract the total marks obtained by the first five students from the total marks obtained by all six students: 426 - (146 + 204) = 76 marks.
Therefore, the mark obtained by the sixth student is 76%.
Lexie, a bowler, claims that her bowling score is more than 140 points, on average. Several of her teammates do not believe her, so she decides to do a hypothesis test, at a 5% significance level, to persuade them. She bowls 18 games. The mean score of the sample games is 155 points. Lexie knows from experience that the standard deviation for her bowling score is 17 points. H0: μ=140; Ha: μ>140 α=0.05 (significance level) What is the test statistic (z-score) of this one-mean hypothesis test, rounded to two decimal places?
Answers
Answer:
The test statistic is \(t = 3.744\)
Step-by-step explanation:
From the question we are told that
The population mean is \(\mu = 140\)
The The level of significance is \(\alpha = 0.05\)
The sample size is n = 18
The null hypothesis is \(H_o : \mu = 140\)
The alternative hypothesis is \(H_a : \mu > 140\)
The sample mean is \(\= x = 155\)
The standard deviation is \(\sigma = 17\)
Generally the test statistics is mathematically represented as
\(t = \frac{\= x - \mu }{ \frac{ \sigma}{ \sqrt{n} } }\)
substituting values
\(t = \frac{ 155 - 140 }{ \frac{ 17 }{ \sqrt{18} } }\)
\(t = 3.744\)
This graph shows how fast a commuter train travels on its route in an urban area. What is the meaning of the point with an x-coordinate of 4
Answers
The meaning of the point with an x-coordinate of 2 is in 2 seconds, the commuter travels 120 feet.
What is an equation?An equation is an expression that shows the relationship between two or more numbers and variables.
Independent variables represent function inputs that do not depend on other values, while dependent variables represent function outputs that depends on other values.
From the graph, the x coordinate 2, have a y coordinate of 120. Hence:
The meaning of the point with an x-coordinate of 2 is in 2 seconds, the commuter travels 120 feet.
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1

Polygon Cand polygon D are similar. The perimeter of polygon C is 48 inches,
and the perimeter of polygon D is 12 inches. If one side of polygon C is 8
inches, what is the length of the corresponding side in polygon D?
OA. 32 in
OB. 8 in
C. 64 in
OD. 2 in
SUBMIT
Answers
option D is the correct answer. The length of the corresponding side in polygon D is 2 inches.
As it is given that the polygon is similar
That means that the ratio of the perimeter of the polygon will be equal to the ratio of the corresponding sides.
perimeter of polygon C/Perimeter of polygon D = side of C/side of D
⇒ 192/48=8/length of the corresponding side(let us consider x)
⇒ 192/48=8/x ⇒ x = 8*48/192 = 2 inches.
Hence, the length of the corresponding side in Polygon D is 2 inches.
Therefore, option D is the correct answer.
learn more about polygon here:
https://brainly.com/question/10441863
#SPJ9
Four less than the product of a number (x)
and 5 is equal to 8 more than 2 added to
3 times the number. Which of these equa-
tions could be used to find the value of x?
Answers
Answer: The equation used to find the value of x is 5x - 4 = 3x + 10. The value of x is determined to be 7.
Step-by-step explanation:
Four less than the product of a number (x) and 5 = 5x - 4
8 more than 2 added to 3 times the number = 3x + 2 + 8 = 3x + 10
Four less than the product of a number (x) and 5 is equal to 8 more than 2 added to 3 times the number => 5x - 4 = 3x + 10
5x - 3x = 10 + 4
2x = 14
x = 14/2
therefore, x = 7
To know more about Algebra,
https://brainly.com/question/28871326
AX'Y'Z' is a dilation of AXYZ Identify the type of dilation and find the scale factor. AY 7 6 5 N IY 4 2 Z' 1 X' 1 2 3 4 5 6 7 8 enlargement O reduction The scale factor is PREV 3 4 5 6 7 SUBMIT O 9

Answers
Dilation with center at origin is given by the formula
\(\begin{gathered} D_{O,k}(x,y)=(kx,ky) \\ \text{Where O is the center of dilation at (0,0) and k is the scale factor} \end{gathered}\)So, in this case, you have
\(\begin{gathered} X^{\prime}(0,0)\rightarrow X(0,0) \\ Y^{\prime}(0,4)\rightarrow Y(0,8) \\ Z^{\prime}(2,3)\rightarrow Z(4,6) \end{gathered}\)You can see that the value of k is 2 because
\(\begin{gathered} X^{\prime}(0,0)\rightarrow X(2\cdot0,2\cdot0)=X(0,0) \\ Y^{\prime}(0,4)\rightarrow Y(2\cdot0,2\cdot4)=Y(0,8) \\ Z^{\prime}(2,3)\rightarrow Z(2\cdot2,2\cdot3)=Z(4,6) \end{gathered}\)Finally, since k > 1 then the dilation is an enlargement.
Which expression is equivalent to 3(x-6)+5(x-4)
Answers
Answer:
\(8x-38\)
Step-by-step explanation:
\(3(x-6)+5(x-4)\\3x-18+5x-20\\3x+5x-18-20\\8x-38\)
Let Q be an orthogonal matrix with an eigenvalue λ1=1. Let x be an eighenvector beloinging to λ1. Show that x is also an eigenvector of QT
Answers
If Q is an orthogonal matrix with an eigenvalue λ1 = 1, then x, the eigenvector corresponding to λ1, is also an eigenvector of QT with an eigenvalue λ2 = λ1 * (QT * x).
To show that x is also an eigenvector of QT, we need to demonstrate that QT * x is a scalar multiple of x.
Given that Q is an orthogonal matrix, we know that QT * Q = I, where I is the identity matrix. This implies that Q * QT = I as well.
Let's denote x as the eigenvector corresponding to the eigenvalue λ1 This means that Q * x = λ1 * x.
Now, let's consider QT * x. We can multiply both sides of the equation Q * x = λ1 * x by QT:
QT * (Q * x) = QT * (λ1 * x)
Applying the associative property of matrix multiplication, we have:
(QT * Q) * x = λ1 * (QT * x)
Using the fact that Q * QT = I, we can simplify further:
I * x = λ1 * (QT * x)
Since I * x equals x, we have:
x = λ1 * (QT * x)
Now, notice that λ1 * (QT * x) is a scalar multiple of x, where the scalar is λ1. Therefore, we can rewrite the equation as:
x = λ2 * x
where λ2 = λ1 * (QT * x).
This shows that x is indeed an eigenvector of QT, with the eigenvalue λ2 = λ1 * (QT * x).
In conclusion, if Q is an orthogonal matrix with an eigenvalue λ1 = 1, then x, the eigenvector corresponding to λ1, is also an eigenvector of QT with an eigenvalue λ2 = λ1 * (QT * x).
for more such question on matrix visit
https://brainly.com/question/2456804
#SPJ8
If $84 interest was earned on $600 principal at a
7% interest rate, how long was the money in the account?
Answers
Answer:
The time is 2 years
Step-by-step explanation:
we know that
The simple interest formula is equal to
A=P(1+rt)
where
A is the Final Investment Value
P is the Principal amount of money to be invested
r is the rate of interest
t is Number of Time Periods
in this problem we have
t= ? years
P= $600
A= $600 + $84 = $684
r = 0.07
substitute in the formula above
$684 = $600(1+(0.07)t)
solve for t
t = [(684/600) - 1]/0.07 = 2 years
Find the area of the region bounded by
• y = √x,
• y = 2-x², and
y = -√2x.
Answers
The area of the Region bounded by y = √x, y = 2-x², and y = -√2x is $\frac{32}{15}$.
To find the area of the region bounded by y = √x, y = 2-x², and y = -√2x, we need to graph the equations and determine the points of intersection. Then we can integrate to find the area.
Firstly, we'll graph the equations and find the points of intersection:
y = √xy = 2-x²y = -√2xGraph of y = √x, y = 2-x², and y = -√2xWe need to solve for the points of intersection, so we'll set the equations equal to each other and solve for x:√x = 2-x²√x + x² - 2 = 0Let's substitute u = x² + 1:√x + u - 3 = 0√x = 3 - u
(Note: Since we squared both sides, we have to check if the solution is valid.)u = -2x²u + x² + 1 = 0 (substituting back in for u
)Factoring gives us:u = (1, -2)We can then solve for x and y:x = ±1, y = 1y = 2 - 1 = 1, x = 0y = -√2x = -√2, x = 2y = 0, x = 0Graph of y = √x, y = 2-x², and y = -√2x with points of intersection to find the area, we need to integrate.
The area is bounded by the x-values -1 to 2, so we'll integrate with respect to x:$$\int_{-1}^0 (2 - x^2) - \sqrt{x} \ dx + \int_0^1 \sqrt{x} - \sqrt{2x} \ dx$$
We can then simplify and integrate:$$\left[\frac{2x^3}{3} - \frac{2x^{5/2}}{5/2} + \frac{4}{3}x^{3/2}\right]_{-1}^0 + \left[\frac{2x^{3/2}}{3} - \frac{4x^{3/2}}{3}\right]_0^1$$$$= \frac{4}{3} + \frac{4}{3} - \frac{4}{15} + \frac{4}{3} - \frac{4}{3}$$$$= \frac{32}{15}$$
Therefore, the area of the region bounded by y = √x, y = 2-x², and y = -√2x is $\frac{32}{15}$.
For more questions on Region .
https://brainly.com/question/31408275
#SPJ8
PLEASE HELP!! What is the surface area of the cone?
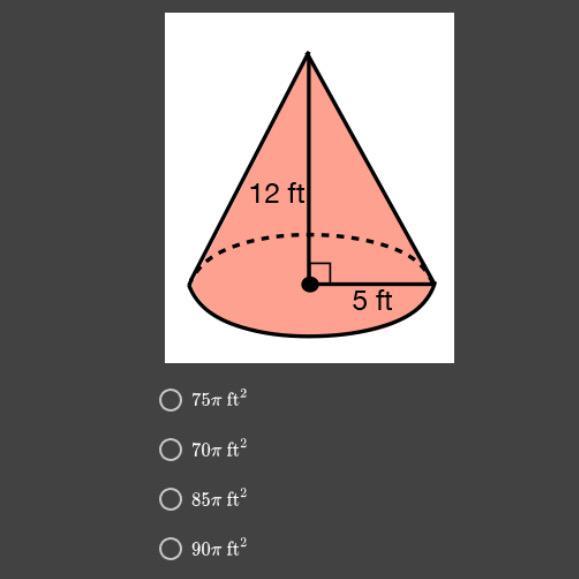
Answers
Hope this helped
The outside temperature was 2 degrees C. The temperature decressed by 4 degrees C. That was the resulting temperature?
Answers
Answer:
-2
Step-by-step explanation:
2-4=-2
True or False
An art historian researches the background information on an artist and his/her works.
Answers
Answer:
true
Step-by-step explanation:
Answer:
true
Step-by-step explanation:
In a right-angled triangle the ratio of the two smaller angles is 3:2. Find the sizes of each of the angles.
Answers
Answer:
36° , 54° , 90°
Step-by-step explanation:
since the triangle is right then one angle is 90°
the ratio of the smaller angles = 3 : 2 = 3x : 2x ( x is a multiplier )
the sum of the 3 angles in the triangle is 180° , that is
3x + 2x + 90 = 180
5x + 90 = 180 ( subtract 90 from both sides )
5x = 90 ( divide both sides by 5 )
x = 18
Then
3x = 3 × 18 = 54°
2x = 2 × 18 = 36°
the 3 angles measure 36° , 54° , 90°
Seth is using the figure shown below to prove Pythagorean Theorem using triangle similarity:
In the given triangle ABC, angle A is 90° and segment AD is perpendicular to segment BC.
The figure shows triangle ABC with right angle at A and segment AD. Point D is on side BC.
Which of these could be a step to prove that BC2 = AB2 + AC2?
possible answers -
By the cross product property, AB2 = BC multiplied by BD.
By the cross product property, AC2 = BC multiplied by BD.
By the cross product property, AC2 = BC multiplied by AD.
By the cross product property, AB2 = BC multiplied by AD.

Answers
The correct step to prove that \(BC^2 = AB^2 + AC^2\) is:
By the cross product property, \(AC^2 = BC \cdot AD\).
To prove that \(BC^2 = AB^2 + AC^2\), we can use the triangle similarity and the Pythagorean theorem. Here's a step-by-step explanation:
Given triangle ABC with right angle at A and segment AD perpendicular to segment BC.
By triangle similarity, triangle ABD is similar to triangle ABC. This is because angle A is common, and angle BDA is a right angle (as AD is perpendicular to BC).
Using the proportionality of similar triangles, we can write the following ratio:
\($\frac{AB}{BC} = \frac{AD}{AB}$\)
Cross-multiplying, we get:
\($AB^2 = BC \cdot AD$\)
Similarly, using triangle similarity, triangle ACD is also similar to triangle ABC. This gives us:
\($\frac{AC}{BC} = \frac{AD}{AC}$\)
Cross-multiplying, we have:
\($AC^2 = BC \cdot AD$\)
Now, we can substitute the derived expressions into the original equation:
\($BC^2 = AB^2 + AC^2$\\$BC^2 = (BC \cdot AD) + (BC \cdot AD)$\\$BC^2 = 2 \cdot BC \cdot AD$\)
It was made possible by cross-product property.
Therefore, the correct step to prove that \(BC^2 = AB^2 + AC^2\) is:
By the cross product property, \(AC^2 = BC \cdot AD\).
For more questions on cross-product property:
https://brainly.com/question/14542172
#SPJ8
Determine the mean, median, mode and midrange for the following data:
13 15 18 18 21
Your answers should be exact numerical values.
The mean of the data is
The median of the data is
The mode of the data is
The midrange of the data is
Answers
The Mean is 17, Median is 18, Mode is 18 and, Midrange is 17.
The Mean is defined as the ratio of sum of numbers present in the data to the total numbers present in the data. Median is defined as the ratio of sum of middle numbers present in the data. Mode is defined as the most recurring number present in the data. Midrange is the ratio of the largest and smallest number in the data to 2.
Let's see how to calculate Mean, Median, Mode and Midrange.
Mean = 13 + 15 + 18 + 18 + 21 / 5
Mean = 85 / 5
Mean = 17
Median = 18 (as it is the middle term of the data)
Mode = 18 (as it is most recurring number)
Midrange = 21 + 13 / 2
Midrange = 34 / 2
Midrange = 17
Therefore, The Mean is 17, Median is 18, Mode is 18 and, Midrange is 17.
To study more about Mean, Median Mode:
https://brainly.com/question/14532771
https://brainly.com/question/542771
Multiply (4.12 × 10−9)(8.3 × 1015). Write the final answer in scientific notation.
34.196 × 10−134
3.4196 × 107
3.4196 × 10−135
34.196 × 106
Omg, I'm just stuck on this question, please help loves
Answers
Answer:
\(3.4196 \times 10^{7}\)
Step-by-step explanation:
Given expression:
\((4.12 \times 10^{-9})(8.3 \times 10^{15})\)
Remove the parentheses:
\(\implies 4.12\times 10^{-9} \times 8.3 \times 10^{15}\)
Collect like terms:
\(\implies 4.12 \times 8.3 \times 10^{-9} \times 10^{15}\)
Multiply the numbers 4.12 and 8.3:
\(\implies 34.196 \times 10^{-9} \times 10^{15}\)
\(\textsf{Apply exponent rule} \quad a^b \cdot a^c=a^{b+c}:\)
\(\implies 34.196 \times 10^{(-9+15)}\)
\(\implies 34.196 \times 10^{6}\)
Scientific notation is written in the form \(\boxed{a \times 10^n}\)
where \(1\leq a < 10\) and \(n\) is any positive or negative whole number.
To convert 34.196 × 10⁶ into scientific notation, move the decimal point to the left by one place and increase the power of 10 by 1:
\(\implies 34.196 \times 10^{6}=3.4196 \times 10^{7}\)
I'm trying to figure out the solve this quadratic function and I had a tutor helping me but my phone lost connection and I only made it halfway through this is the problem I will take a picture

Answers
Given a function as shown below:
\(P(x)=550x-1240-2x^2\)\(\begin{gathered} for\text{ profit maximization } \\ P(x)=550x-1240-2x^2 \\ \frac{dp(x)}{dx}=550-4x \\ 0\text{ = 550 -4x} \\ 4x\text{ = 550} \\ x=\text{ }\frac{550}{4} \\ x=137.5 \\ x=\text{ 138 (nearest whole number)} \end{gathered}\)Hence to maximize the profit at least 138 items must be sold
And the maximum profit that can be earned is derived by substituting 138 it to p(x)
\(\begin{gathered} P(x)=550x-1240-2x^2 \\ P(x)=550(138)-1240-2(138)^2 \\ P(x)=\text{ 36572}.00 \end{gathered}\)Hence the maximum profit is $36572.00
The minimum item that must be sold to make a profit can be found by solving the following quadratic inequality:
\(P(x)=550x-1240-2x^2\ge0\)And the solution is given as
\(\begin{gathered} \frac{-\sqrt{73145}+275}{2}\le\: x\le\frac{\sqrt{73145}+275}{2} \\ 2.27333\le\: x\le\: 272.72666 \end{gathered}\)Hence, the company must sell a minimum of 3 items to make a profit
WILL GIVE BRAINLEST 658 minus what equals 98?
Answers
Answer:
-560 is the answer
Step-by-step explanation:
658 - (-560 )= 98
Answer:
Hello!!! erz here ^^
Step-by-step explanation:
658 - 560 = 98
Hope this helps!! :D