The Fibonacci sequence is 0, 1, 1, 2, 3, 5, 8, 13, . . . (where F0 0).
(a) Give the recursive definition for the sequence.
(b) Write out the first few terms of the sequence of partial sums: 0, 0 + 1, 0 + 1 + 1,. . .
(c) Give a closed formula for the sequence of partial sums in terms of Fn (for example, you might say F0 + F1 + · · · + Fn 3F 2 n−1 + n, although that is definitely not correct).
(Discrete Mathematics)
Answers
The Fibonacci sequence is the sequence in which the numbers are written such that each succeeding number is sum of two preceding numbers.
The Fibonacci sequence is defined recursively as follows:
F0 = 0
F1 = 1
For n > 1, Fn = Fn-1 + Fn-2
(b) The sequence of partial sums is:
S0 = 0
S1 = 0 + 1 = 1
S2 = 0 + 1 + 1 = 2
S3 = 0 + 1 + 1 + 2 = 4
S4 = 0 + 1 + 1 + 2 + 3 = 7
S5 = 0 + 1 + 1 + 2 + 3 + 5 = 12
(c) A closed formula for the sequence of partial sums in terms of Fn is not possible, since the sequence of partial sums depends on the values of all previous terms in the Fibonacci sequence. However, it is possible to express the nth term of the sequence of partial sums, Sn, in terms of the nth term of the Fibonacci sequence, Fn, using the following formula:
Sn = F0 + F1 + ... + Fn = (F0 + F1) + (F1 + F2) + ... + (Fn-1 + Fn) = F1 + F2 + ... + Fn + F0 + F1 + ... + Fn-1 = 2Sn-1 - Fn + F0
This formula can be derived by considering the previous term in the sequence of partial sums and adding the current term of the Fibonacci sequence to it.
Learn more about Fibonacci sequence at:
brainly.com/question/1296660
#SPJ4
Related Questions
A programmer plans to develop a new software system. In planning for the operating system that he will use, he needs to estimate the percentage of computers that use a new operating system. How many computers must be surveyed in order to be 95% confident that his estimate is in error by no more than 4 percentage points? Complete parts (a) through (c) below.
A. Assume that nothing is known about the percentage of computers with new operating systems. (round up to the nearest integer)
n = ?
Answers
To be 95% confident that the estimate of the Percentage of computers with a new operating system is in error by no more than 4 percentage points, the programmer needs to survey at least 601 computers.
The sample size (n) needed to estimate the percentage of computers using a new operating system with a 95% confidence level and an error margin of no more than 4 percentage points, we need to use the formula for sample size estimation for proportions.
The formula is:
n = (Z^2 * p * (1-p)) / E^2
Where:
- n is the sample size
- Z is the z-score corresponding to the desired confidence level (for 95% confidence level, the z-score is approximately 1.96)
- p is the estimated proportion (since nothing is known about the percentage of computers with the new operating system, we assume p = 0.5 for maximum variability)
- E is the desired margin of error (in this case, 4 percentage points, which is 0.04 in decimal form)
Now, let's substitute the values into the formula and calculate the sample size (n)
n = (1.96^2 * 0.5 * (1-0.5)) / 0.04^2
n = (3.8416 * 0.25) / 0.0016
n = 0.9604 / 0.0016
n ≈ 600.25
Since the sample size must be a whole number, we round up to the nearest integer.
n = 601
Therefore, to be 95% confident that the estimate of the percentage of computers with a new operating system is in error by no more than 4 percentage points, the programmer needs to survey at least 601 computers.
For more questions on Percentage .
https://brainly.com/question/30637655
#SPJ8
if y is directly porportional to x^2 and the difference in the values of y when x=1 and x=3 is 32, find the value of y when x=-2
Answers
Answer:
Step-by-step explanation:
y=kx²
y₁=k(1)²=k
y₃=k(3)²=9k
y₁-y₃=k-9k=32
-8k=32
k=-4
y=-4x²
y₋₂=-4(-2)²=-16
Help on this algebra 2 question!!!!!!

Answers
Answer:
C.
Ax + 1 = x A + 1
Bx + 2 = x B + 2
Cx + 3 = x C + 3
A = x C + 3
B = x C + 3
C = x C + 3
I'm not really sure about the answer but i hope it helps
Solve for m.m- 15 = 20
Answers
Answer:
m=35
Explanation:
Given the equation:
\(m-15=20\)We solve for the value of m by adding 15 to both sides.
\(\begin{gathered} m-15+15=20+15 \\ m+0=35 \\ m=35 \end{gathered}\)The value of m is 35.
The result will be m=35
Please help me with this.

Answers
Here are the correct matches to the expressions to their solutions.
The GCF of 28 and 60 is 4.
(-3/8)+(-5/8) = -4/4 = -1.
-1/6 DIVIDED BY 1/2 = -1/6 X 2 = -1/3.
The solution of 0.5 x = -1 is x = -2.
The solution of 1/2 m = 0 is m = 0.
-4 + 5/3 = -11/3.
-2 1/3 - 4 2/3 = -10/3.
4 is not a solution of -4 < x.
1. The GCF of 28 and 60 is 4.
The greatest common factor (GCF) of two numbers is the largest number that is a factor of both numbers. To find the GCF of 28 and 60, we can factor each number completely:
28 = 2 x 2 x 7
60 = 2 x 2 x 3 x 5
The factors that are common to both numbers are 2 and 2. The GCF of 28 and 60 is 2 x 2 = 4.
2. (-3/8)+(-5/8) = -1.
To add two fractions, we need to have a common denominator. The common denominator of 8/8 and 5/8 is 8. So, (-3/8)+(-5/8) = (-3 + (-5))/8 = -8/8 = -1.
3. -1/6 DIVIDED BY 1/2 = -1/3.
To divide by a fraction, we can multiply by the reciprocal of the fraction. The reciprocal of 1/2 is 2/1. So, -1/6 DIVIDED BY 1/2 = -1/6 x 2/1 = -2/6 = -1/3.
4. The solution of 0.5 x = -1 is x = -2.
To solve an equation, we can isolate the variable on one side of the equation and then solve for the variable. In this case, we can isolate x by dividing both sides of the equation by 0.5. This gives us x = -1 / 0.5 = -2.
5. The solution of 1 m = 0 is m = 0.
To solve an equation, we can isolate the variable on one side of the equation and then solve for the variable. In this case, we can isolate m by dividing both sides of the equation by 1. This gives us m = 0 / 1 = 0.
6. -4 + 5/3 = -11/3.
To add a fraction and a whole number, we can convert the whole number to a fraction with the same denominator as the fraction. In this case, we can convert -4 to -4/3. So, -4 + 5/3 = -4/3 + 5/3 = -11/3.
7. -2 1/3 - 4 2/3 = -10/3.
To subtract two fractions, we need to have a common denominator. The common denominator of 1/3 and 2/3 is 3. So, -2 1/3 - 4 2/3 = (-2 + (-4))/3 = -6/3 = -10/3.
8. 4 is not a solution of -4 < x.
The inequality -4 < x means that x must be greater than -4. The number 4 is not greater than -4, so it is not a solution of the inequality.
For more such questions on GCF
https://brainly.com/question/902408
#SPJ8
1. Write down the four inequality symbols and give an example to show what each one means.
Answers
The four inequality symbols are,
\(<,>,\leq,and\ge\)The example for each one of inequality symbol are,
\(x<4\)In this inequality, possible values of x are less than 4 (not including 4). x can takes all the values that are less than 4.
Second inequality,
\(x>4\)In this inequality x takes all the value that are greater than 4 (not including 4). x takes all the values more than 4.
Third inequality,
\(x\leq4\)In this inequality x takes all possible values of x less than 4 but also include 4. x can takes all the value less than or equal to 4. In this x can also be equal to 4.
Fourth inequality,
\(x\ge4\)In this inequality x takes all possible value that are more than 4 and equal to 4 (It include 4 also). x can takes all values more than or equal to 4. In this inequality x can also be equal to 4.
The points (a,b) and (c,d) form a segment, and the points (d,e) and (d,f) form a segment. Create an equation assuming the segments are congruent
Answers
If the segments are congurent they are of equal length.
So constructing an equation will not be hard.
Take for example \(y=x\) and limit x to be between and including 0 and 1 for the first segment. In this case our segment is \((a,b)\to(c,d)=(0,0)\to(1,1)\).
Now, d has been fixated to the value of 1 and we need to construct a segment from \((1,e)\to(1,f)\).
Since both x coordinates of the endpoints of the segment are fixed to be 1, we cannot run anymore, that is, we fixated our run. But on the rise (y-axis direction) we can still move one unit up.
Let e be 1 and f be 2. The distance between \((1,1)\) and \((1,2)\) is 1 which is also the distance between \((0,0)\) and \((1,1)\).
Now we are asked to find the equation of both segments.
First segment is described by \(y=x\) with limited domain of \(0\leq x\leq1\).
Second segment is described by \(x=2\) with again limited domain of \(1\leq y\leq2\).
Hope this helps :)
The length, l of a segment with points (x₁, y₁), and (x₂, y₂) is presented as follows; \(l = \sqrt{\left (y_{2}-y_{1} \right )^{2}+\left (x_{2}-x_{1} \right )^{2}}\)
An equation that can be created given that the segment with points (a, b) and (c, d), and the segment with points (d, e), and (d, f) are congruent is presented as follows;
√((d - b)² + (c - a)²) = f - e
The reason the above equation is correct is presented as follows;
Given that the segments are congruent, therefore;
Length of (a, b) and (c, d) = Length of (d, e) and (d, f)
Length of (a, b) and (c, d) = √((d - b)² + (c - a)²)
Length of (d, e) and (d, f) = √((f - e)² + (d - d)²) = f - e
Which gives the equation;
√((d - b)² + (c - a)²) = f - e
Learn more about segments in the coordinate plane here:
https://brainly.com/question/14817604
need this asap! questions in the ss


Answers
Answer/Step-by-step explanation:
Part A:
Evidence 1: the line passes through the point of origin, (0, 0)
Evidence 2: it has a unit rate or constant of proportionality, k = y/x = 5/3
Part B:
When extended, if the ray passes through the point, (18, 30), then y/x of this point, should give us the same unit rate (k) of 5/3 of the graph.
Thus:
y/x = 30/18
Simplify
= 5/3
Thus, it has the same unit rate of the graph, therefore, the ray passes through the point (18, 30).
Maya is riding on a bike course that is 35 miles long. So far, she has ridden 14 miles of the course. What percentage of the course has Maya ridden so far
Answers
Answer:
40%
Step-by-step explanation:
Find the percentage she has ridden so far by dividing 14 by 35:
14/35
= 0.4
So, Maya has ridden 40% of the course
Answer: 40%
Step-by-step explanation: i went to a percentage calculator and found out what it was
2//2/2/3/2/2//3/3/3//3/3/4/5/5
Answers
Answer:
can u be more specific so i can properly help u
Explanation:
pls explain and i will edit my answer
Can somebody please help with this? I've been stuck on it for a while

Answers
Answer:
b
Step-by-step explanation:
positive linear means more of this = more of the other.
and that's what it looks like it's doing. bigger screen = more hours
What is the volume, in cubic in, of a rectangular prism with a height of 11in, a width
of 15in, and a length of 2in?
Answers
\(330in^{3}\)
I'm pretty sure that's the answer
Pls help me I am stuck tysm

Answers
a) The initial deposit in the account is given as follows: 1,287.39 euros.
b) The interest rate of the account is given as follows: 3%.
How to obtain the balance using simple interest?The equation that gives the balance of an account after t years, considering simple interest, is modeled as follows:
A(t) = P(1 + rt).
In which the parameters of the equation are listed and explained as follows:
A(t) is the final balance.P is the value of the initial deposit.r is the interest rate, as a decimal.t is the time in years.Considering the balances after 5 and 6 years, the interest rate is obtained as follows:
r = 1524.60/1480.50 - 1
r = 0.03.
Considering the balance after 5 years, the initial deposit is obtained as follows:
P(1 + 0.03 x 5) = 1480.5
P = 1480.5/1.15
P = 1,287.39 euros.
More can be learned about simple interest at https://brainly.com/question/20690803
#SPJ1
Whoever knows the answer tell me please thank you :)

Answers
Answer:
Ans its 50
Let me know if its incorrect:-)
Answer is:
s = 50
Here's how to solve:
In this inequality, our first step is to find the least common denominator (that applies to both fractions, of course), or LCD. For the LCD, the we must find a number that is a multiple of both 21 and 30, and then multiply both sides of the inequality by said value. The reason we multiply on both sides of the inequality is because of the Line of Equality, which is a ruling that states that what you do on one side of an inequality, you also must do on the other.
In this case, our LCD is 210. After multiplying both sides, we are left with 350 = 7s.
Our next step is to isolate the variable 7s to make it singular. 1s, or s, is what we are trying to change the variable to, since that is what the isolated variable will look like. By dividing 7s by 7, we can successfully isolate the variable to 1s/s. Due to the Line of Equality rule, we should do this to both sides. After dividing each side by 7, we are left with s = 50.
Therefore, the value of s is 50, making the answer s = 50.
Bonus: Showing Work
Finding the LCD;
LCD for 21:
( 21 * 1 , 21 * 2 , 21 * 3 , 21 * 4 , etc... )
Multiples of 21: 21, 42, 63, 84, 105, 126, 147, 168, 189, 210, 231, 252, 273
LCD for 30:
( 30 * 1 , 30 * 2 , 30 * 3 , 30 * 4 , etc... )
Multiples of 30: 30, 60, 90, 120, 150, 180, 210, 240, 270, 300
LCD Found; 210
Multiplying by LCD;
( 35 / 21 * 210 or 35 ÷ 21 * 210 )
Left Side Steps:
Simplify- 35 / 21 --> 35 ÷ 7 / 21 ÷ 7 --> 35 ÷ 7 = 5 & 21 ÷ 7 = 3 --> 5 / 3 ( * 210 )
Single Fraction Format/Format Change- 5 / 3 * 210 --> 5 * 210 / 3
Multiply Numerator(s)/Top- 5 * 210 / 3 --> 5 * 210 = 1050 --> 1050 / 3
Divide Numerator & Denominator- 1050 / 3 or 1050 ÷ 3 --> 350
Right Side Steps:
( s / 30 * 210 or s ÷ 30 * 210 )
Single Fraction Format/Format Change- s / 30 * 210 --> s * 210 / 30
Multiply Numerator(s)/Top- s * 210 / 30 --> 210s / 30
Divide Numerator & Denominator- 210s / 30 or 210s ÷ 30 --> 7s
New Inequality/Equation Found: 350 = 7s
Dividing by 7;
Left Side: 350 ÷ 7 = 50
Right Side: 7s ÷ 7 = s
New Inequality Found; 50 = s, or s = 50 (the sign does not flip because the equivalent sign is the same both ways - and the opposite would be the same as the current value)
Hope this helps! :]
The length of a rectangle is twice its width.
If the perimeter of the rectangle is 42 m, find its length and width.
Answers
Answer:
l = 14 w = 7
Step-by-step explanation:
14 x 2 = 28
7 x 2 - 14
28 + 14 = 42
Two polygonal regions are similar with scale factor 7. The area of the smaller region is 490 cm2. What is the area of the larger region? Explain your reasoning.
Answers
Two polygonal regions are similar with scale factor 7, if the area of the smaller region is 490 cm² then the area of the larger region would be 3430 cm²
What is an equation?An equation is an expression that shows the relationship between two or more numbers and variables.
Dilation is the increase or decrease in the size of a figure by a scale factor.
Two polygonal regions are similar with scale factor 7. The area of the smaller region is 490 cm², hence:
Area of larger region = 7 * 490 cm² = 3430 cm²
Two polygonal regions are similar with scale factor 7, if the area of the smaller region is 490 cm² then the area of the larger region would be 3430 cm²
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
58 students on a bus how many students were fit on a six buses
Answers
Answer:
348
Step-by-step explanation:
James wants to have earned $6,180 amount of interest in 28 years. Currently he finds
that his annual interest rate is 6.12%. Calculate how much money James needs to invest
as his principal in order to achieve this goal.
Answers
Answer:
$3606.44
Step-by-step explanation:
The question asks us to calculate the principal amount that needs to be invested in order to earn an interest of $6180 in 28 years at an annual interest rate of 6.12%.
To do this, we need to use the formula for simple interest:
\(\boxed{I = \frac{P \times R \times T}{100}}\),
where:
I = interest earned
P = principal invested
R = annual interest rate
T = time
By substituting the known values into the formula above and then solving for P, we can calculate the amount that James needs to invest:
\(6180 = \frac{P \times 6.12 \times 28}{100}\)
⇒ \(6180 \times 100 = P \times 171.36\) [Multiplying both sides by 100]
⇒ \(P = \frac{6180 \times 100}{171.36}\) [Dividing both sides of the equation by 171.36]
⇒ \(P = \bf 3606.44\)
Therefore, James needs to invest $3606.44.
Ryan buys lunch for $16.83. If sales tax is 8.4%, How much money does Ryan need total for lunch
Answers
\(\begin{array}{|c|ll} \cline{1-1} \textit{\textit{\LARGE a}\% of \textit{\LARGE b}}\\ \cline{1-1} \\ \left( \cfrac{\textit{\LARGE a}}{100} \right)\cdot \textit{\LARGE b} \\\\ \cline{1-1} \end{array}~\hspace{5em}\stackrel{\textit{8.4\% of 16.83}}{\left( \cfrac{8.4}{100} \right)16.83} ~~ \approx ~~ 1.41~\hfill \underset{ Total~for~lunch }{\stackrel{ 16.83~~ + ~~1.41 }{\approx\text{\LARGE 18.24}}}\)
An unknown polynomial is added to the expression -3x^3+2x-5 and the resulting sum is 4x^3+7x^2-3. what is the unknown polynomial?
Answers
Answer:
7x³ + 7x² + 2x - 8
Step-by-step explanation:
Let the unknown polynomial be a
a + -3x³ + 2x - 5 = 4x³ + 7x² - 3
a = 4x³ + 7x² - 3 - (-3x³ + 2x - 5)
a = 4x³ + 7x² - 3 + 3x³ + 2x - 5
a = 7x³ + 7x² + 2x - 8
f(x) = x + 2
g(x) = 3x² - 5
Find (f.g)(x).
OA. (f g)(x) = 3x³ - 10
OB. (f g)(x) = 3x³ + 6x² - 5x - 10
OC. (f. g)(x) = 3x³ + 10
OD. (f g)(x) = 3x³ + 6x² + 5x + 10
SUBMIT

Answers
Answer:
It's option B, (f • g)(x) = 3x^3 + 6x^2 - 5x - 10
Step-by-step explanation:
In this problem, we are dealing with a branch of functions called composite functions. What the difference is between normal and composite functions is that we instead of defining a value for f(x), take two functions, f(x) and g(x), in the form of f and g. For instance, h(x) = g.
• Take the products of both functions.
f(x)g(x) = 3x²+5 • x-2
• Next, expand the functions. We expand by combining like terms.
= 3x^3 - 6x^2 + 5x - 10
Since the function cannot be simplified further, this leads to option B being our answer.
Hope this helps!
A tank is full of water. Find the work (in ft-lb) required to pump the water out of the spout. Use the fact that water weighs 62.5 lb/ft3. (Round your answer to the nearest whole number.) 3 ft6 ft12 ft A frustum of a cone with a spout is given. The smaller radius is 3 ft, the larger radius is 6 ft, and the height is 12 ft.
Answers
The work required to pump the water out of the spout is approximately 64,307,077 ft-lb
To find the work required to pump the water out of the spout, we need to calculate the weight of the water in the tank and then convert it to work using the formula: work = force × distance.
First, let's calculate the volume of water in the tank. The frustum of a cone can be represented by the formula: V = (1/3)πh(r1² + r2² + r1r2), where r1 and r2 are the radii of the two bases and h is the height.
Given r1 = 3 ft, r2 = 6 ft, and h = 12 ft, we can calculate the volume:
V = (1/3)π(12)(9 + 36 + 18) = 270π ft³
Now, we can calculate the weight of the water using the density of water:
Weight = density × volume = 62.5 lb/ft³ × 270π ft³ ≈ 53125π lb
Next, we convert the weight to force by multiplying it by the acceleration due to gravity (32.2 ft/s²):
Force = Weight × acceleration due to gravity = 53125π lb × 32.2 ft/s² ≈ 1709125π lb·ft/s²
Finally, we can calculate the work by multiplying the force by the distance. Since the water is being pumped out of the spout, the distance is equal to the height of the frustum, which is 12 ft:
Work = Force × distance = 1709125π lb·ft/s² × 12 ft ≈ 20509500π lb·ft ≈ 64307077 lb·ft
for more search question water
https://brainly.com/question/17120212
#SPJ8
A square pyramid has a base edge of 1 meter. The height of each triangular face is 1 meter. What is the pyramid's surface area?
Answers
Answer:
A square pyramid has 5 faces: 1 square base and 4 triangular faces.
The area of the base is:
A = s^2
where s is the length of the base edge.
In this case, s = 1 m, so:
A = 1^2 = 1 m^2
The area of each triangular face is:
A = 1/2 * b * h
where b is the base of the triangle (which is equal to the length of one side of the square base) and h is the height of the triangle (which is given as 1 m).
In this case, b = 1 m and h = 1 m, so:
A = 1/2 * 1 * 1 = 0.5 m^2
The total surface area of the pyramid is the sum of the area of the base and the area of the four triangular faces:
SA = A_base + 4 * A_triangles
SA = 1 + 4(0.5)
SA = 1 + 2
SA = 3 m^2
Therefore, the surface area of the pyramid is 3 square meters.
What is the percentage of the patient |epor
Answers
Answer:
Average annual age-adjusted mortality rate was 0.43 deaths/100 000 inhabitants (95% CI 0.40-0.46). The burden of leprosy deaths was higher among males, elderly, black race/colour and in leprosy-endemic regions. Lepromatous leprosy was the most common clinical form mentioned.
Step-by-step explanation:
Today, about 208,000 people worldwide are infected with leprosy, according to the World Health Organization, most of them in Africa and Asia. About 100 people are diagnosed with leprosy in the U.S. every year, mostly in the South, California, Hawaii, and some U.S. territories.
Regs.
Spinner A and Spinner B below are each to be spun once.
0 18
O 12
6
Spinner A
5
2
4
00
D
3
20 of 21
If the pointer cannot land on a line, how many different outcomes of a number and a color are possible?
v
Spinner B
Yellow
Brown
12 13
Red
Answers
Answer:
Step-by-step explanation:
Regs.
Spinner A and Spinner B below are each to be spun once.
0 18
O 12
6
Spinner A
5
2
4
00
y = 2x² + x - 10 .(factor and zero prod)
Answers
Answer: (x-2)(2x+5)
For a polynomial of the form a x 2 + b x + c
rewrite the middle term as a sum of two terms whose product is a x (times) c = 2 − 10 = − 20 and whose sum is b = 1
2 x 2 − 4 x + 5 x − 10 = 0
2 x ( x − 2 ) + 5 ( x − 2 ) = 0
( x − 2 ) ( 2 x + 5 ) = 0
x − 2 = 0
2 x + 5 = 0
Set the first factor equal to 0
x − 2 = 0
Add 2 to both sides of the equation.
x = 2
Set the next factor equal to 0
2 x + 5 = 0
Subtract 5 from both sides of the equation.
2 x = − 5
Divide each term by 2 and simplify.
x = − 5 /2
The final solution is all the values that make = ( x − 2 ) ( 2 x + 5 ) = 0 = true.
x = 2 , − 5 / 2
dhdhahhdhf
Please help
Which of these triangles is NOT possible?
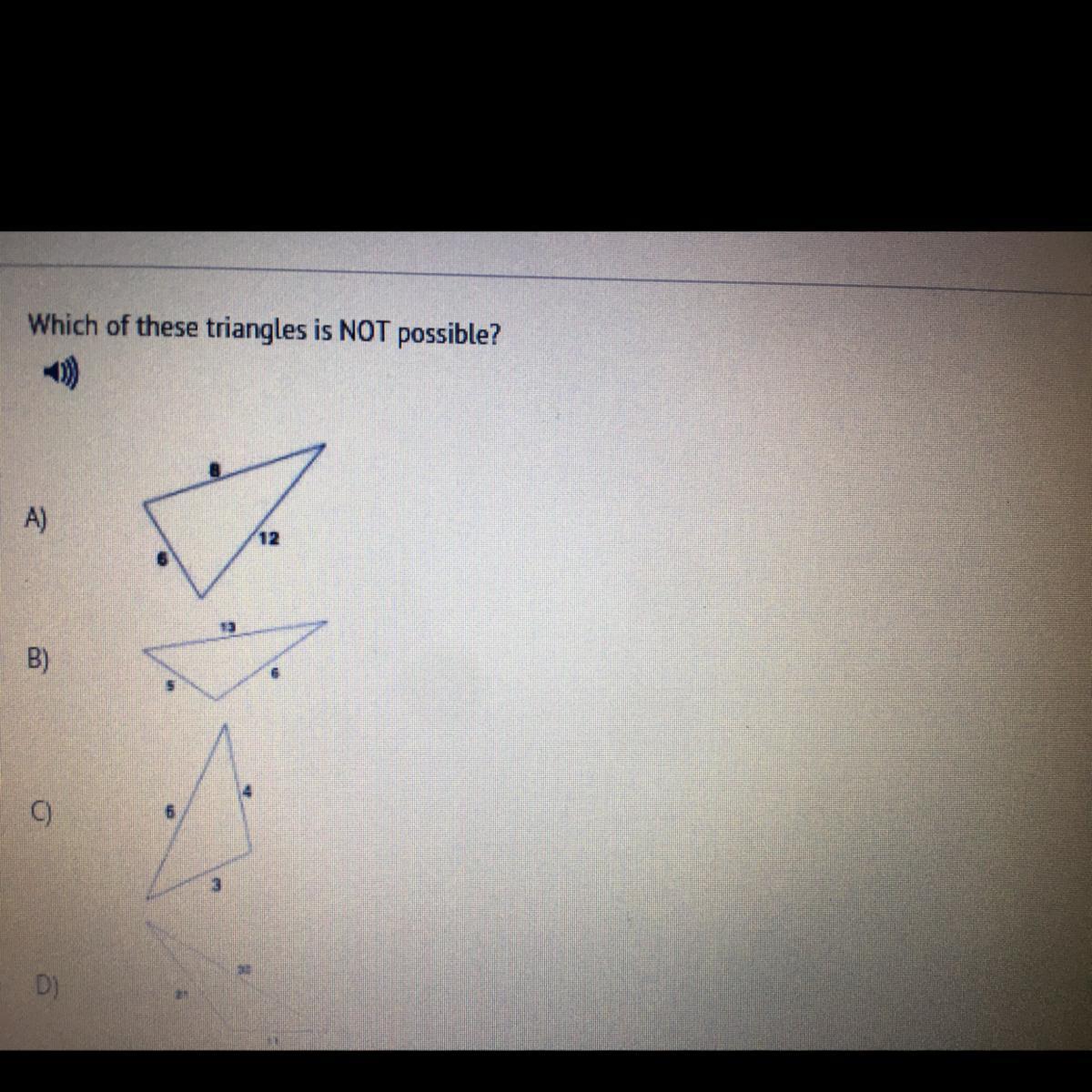
Answers
Answer:
B
Step-by-step explanation:
The sides must be greater than 13 for a triangle to even exist
Answer:
B
Step-by-step explanation:
I Just took the test
Please Help Marked for all my points and will Brainliest
Different sizes of ribbon need to be cut to go around various shapes. All of the following sizes are in inches.
π,√6,2√6,√7
(a) Without using your calculator, approximate the decimal equivalent of each number to the nearest tenth.
(B) Order the ribbon sizes from least to greatest.
Answers
The requreid,
(a) Approximate values of the given numbers are π ≈ 3.1, √6 ≈ 2.4, 2√6 ≈ 4.8, and √7 ≈ 2.6.
(b) √6 < √7 < π < 2√6
(a)
π ≈ 3.1 (since π is between 3 and 4, and is closer to 3.1 than to 3.2)
√6 ≈ 2.4 (since 6 is between 4 and 9, and the square root of 6 is closer to 2.4 than to 2.5)
2√6 ≈ 4.8 (since 2√6 is approximately twice the value of √6, which is 2.4)
√7 ≈ 2.6 (since 7 is between 4 and 9, and the square root of 7 is closer to 2.6 than to 2.7)
(b)
Order from least to greatest:
√6 < √7 < π < 2√6
Learn more about simplification here:
https://brainly.com/question/9912600
#SPJ1
I will vote Brainliest to whoever gets it right.
(It's not 2)
4 = a - 6
Answers
Answer:
its 10
Step-by-step explanation:
add the numbers, 4 and 6 where you'll get 10
Imagine that two researchers, Bill and Ted, independently carry out clinical trials to test the same null hypothesis: H0: COX-2 selective inhibitors (used to treat arthritis) have no effect on the risk of cardiac arrest. They use the same population for their study, but Bill uses a sample size of 60 randomly selected subjects and Ted uses a sample size of 100 randomly selected subjects. Assuming all other aspects of their studies are the same, answer the following:
Required:
a. Whose study has the higher probability of a Type-II error?
b. Whose study has higher power?
c. Whose study has the higher probability of a Type-I error?
d. Should their alternative hypotheses be one-sided or two-sided? Explain
e. Suppose Bill’s analysis results in p-value = 0.03. What should be his conclusion?
Answers
Answer:
A) The 60-subject study will have the higher probability of a Type-II error.
B) 100-subject study will have higher power.
C) they will have the same probability of a Type-I error
D) Two tailed because either of the two results would be of interest
E) If p-value = 0.03, he should reject the null hypothesis if this p-value is less than the significance level. But if it's more than the significance level, he will fail to reject the null hypothesis.
Step-by-step explanation:
A) A type II error is an error that occurs when we accept the null hypothesis even though it is actually false.
Now, Smaller sample sizes usually would have a lesser chance of rejecting the null hypothesis even though it's false. Thus, the 60-subject study will have the higher probability of a Type-II error.
B) power = 1 - Pr(Type II error)
Since the 60-subject study has a higher probability of type II error it means it will have lesser power. Thus, 100-subject study will have higher power.
C) Type I error is when we incorrectly reject a true null hypothesis.
Pr(Type I error) = significance level
Now, since we are told that other aspects of their study are the same it means their significance levels are the same, it means they will have the same probability of a Type-I error
D) It should be two tailed because either of the two results would be of interest. It's either the drug was associated with more cardiac arrests or less potential treatment option.
E) If p-value = 0.03, he should reject the null hypothesis if this p-value is less than the significance level. But if it's more than the significance level, he will fail to reject the null hypothesis.