The farm's owner wants to increase the income from the sale of strawberries to at least $70,000 per year. What change would you suggest that would allow the farm's owner to meet this goal?
Answers
Answer:
Possible changes —
(i) Increase farmland
(ii) Sow healthy strawberry seeds
(iii) Choose a nutrient-rich, suitable plot of land
Related Questions
Given the drawing as shown below and that pllq. Which of the following cannot be supported by the evidence shown? Worth 10 points

Answers
The relation that can not be supported by the evidence in the image is option B
What happens when a transversal cuts a parallel line?
Corresponding angles are those that are located on the same side of the transversal and in identical relative positions to the parallel lines. Angles that correspond to one another have the same measure.
Alternate interior angles are those that are located on the transverse and within the area between the parallel lines, respectively. Congruent alternate interior angles exist.
Alternate external angles are those that are outside of the space between the parallel lines and on the opposing sides of the transversal. Congruent external angles exist between the two.
Learn more about transversal:https://brainly.com/question/17987539
#SPJ1
GIVING OUT BRAINLIST QUICK! I CAN ONLY GIVE BRAINLIST IF 2 PEOPLE ANSWER!

Answers
Answer: 7 i think
Step-by-step explanation:
Answer: Octagon & 6.2
Step-by-step explanation:
octagons have 8 sides and 3.1 x 4 = 12.4 divided by 2 = 6.2
Imagine math Item 994395
Start with the equation 0.2=0 to explain why -4-2 must equal -8.
Drag descriptions and equations to the table to complete the explanation.
Answers
In order to explain why -4 - 2 equals -8, let's start with the equation 0.2 = 0. By analyzing this equation, we can uncover the reason behind this seemingly counterintuitive result.
1. Begin with the equation 0.2 = 0.
2. Subtract 0.2 from both sides of the equation to isolate the variable: 0.2 - 0.2 = 0 - 0.2.
This simplifies to 0 = -0.2.
3. Observe that the right side of the equation, -0.2, is a negative number.
4. Recall that subtracting a negative number is equivalent to adding its positive counterpart. Therefore, -0.2 is the same as +0.2.
5. Rewrite the equation as 0 = +0.2.
6. Notice that 0 on the left side of the equation is equal to 0 + 0, since any number added to zero remains unchanged.
7. Substitute 0 + 0 for 0 in the equation: 0 + 0 = +0.2.
8. Simplify the equation to 0 = +0.2.
9. Finally, recognize that a positive number cannot equal zero. Hence, the equation 0 = +0.2 is false.
10. As a result, the original equation 0.2 = 0 is invalid.
11. Therefore, the logical consequence is that any subsequent deductions based on this invalid equation would also be incorrect.
12. Consequently, -4 - 2 does not equal -8, as per the explanation derived from the flawed equation.
To summarize, by analyzing the equation 0.2 = 0, we can determine that subsequent deductions based on this equation are incorrect. Hence, -4 - 2 does not equal -8.
For more such questions on counterintuitive, click on:
https://brainly.com/question/17004386
#SPJ8
Given the polynomial 9x2y6 − 25x4y8, rewrite as a product of polynomials.
(9xy3 − 25x2y4)(xy3 + x2y4)
(9xy3 − 25x2y4)(xy3 − x2y4)
(3xy3 − 5x2y4)(3xy3 + 5x2y4)
(3xy3 − 5x2y4)(3xy3 − 5x2y4)
Answers
Answer:
Option 3
(3xy³ + 5x²y⁴) (3xy³ - 5x²y⁴)
Step-by-step explanation:
Factorize polynomials:
Use exponent law:
\(\boxed{\bf a^{m*n}=(a^m)^n} \ & \\\\\boxed{\bf a^m * b^m = (a*b)^m}\)
9x²y⁶ = 3²* x² * y³*² = 3² * x² * (y³)² = (3xy³)²
25x⁴y⁸ = 5² * x²*² * y⁴*² = 5² * (x²)² * (y⁴)² = (5x²y⁴)²
Now use the identity: a² - b² = (a +b) (a -b)
Here, a = 3xy³ & b = 5x²y⁴
9x²y⁶ - 25x⁴y⁸ = 3²x²(y³)² - 5²(x²)² (y⁴)²
= (3xy³)² - (5x²y⁴)²
= (3xy³ + 5x²y⁴) (3xy³ - 5x²y⁴)
A travel agent calculates the cost of a trip to Paris using this formula C = p(t + 30)
C is the total cost in pounds
p is the number of people
t is the cost of the trip per person
Use this formula to calculate the total cost if p = 2 and t = 245.
Answers
Answer:
C = £515
Step-by-step explanation:
c= p(t+30)
C= 2(245 + 30)
C=2(275)
C=515
Malcolm has $50 gift card to a local car wash and order is the ultimate car wash each visit is $8.95
Answers
The amount cheaper is the car washes Malcolm orders than the car washes Martha's order is $13.
The correct answer choice is option B.
How much cheaper is the car washes Malcolm orders than the car washes Martha's order?Malcolm's gift card = $50.
Cost Malcolm's car wash per visit = $7
Martha's gift card = $180
Cost Martha's car wash per visit = Difference between gift card balance of first and second visit
= $180 - $160
= $20
How cheap is the car washes Malcolm orders than the car washes Martha's order = $20 - $7
= $13
Therefore, Malcolm's car wash is cheaper than Martha's car wash by $13
The complete question is attached in the diagram.
Read more on graphs:
https://brainly.com/question/19040584
#SPJ1

My teacher said this is all due TODAY I need help ASAP please
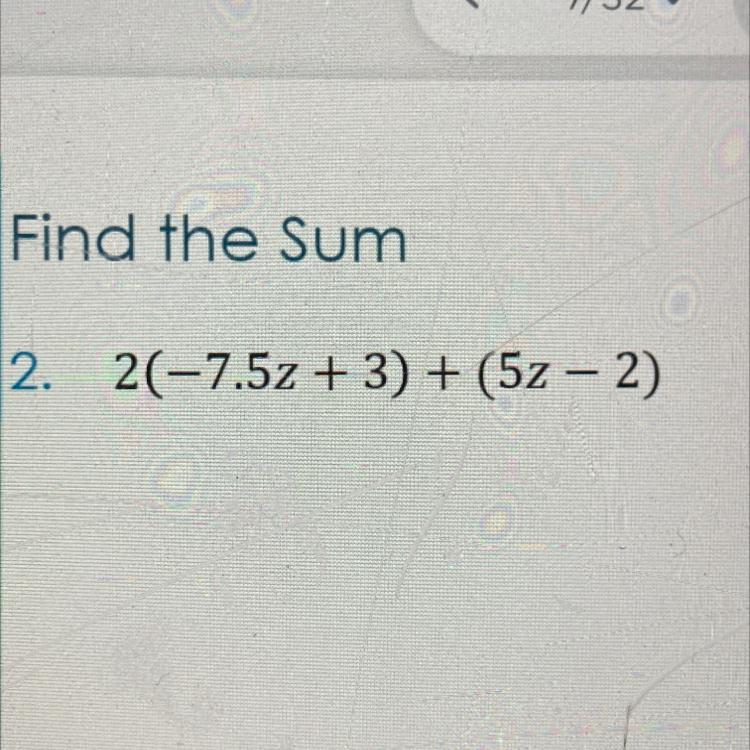
Answers
Answer:
i love you :)
Step-by-step explanation:
you just have to mutliply the first one and sum both of them
(-15z + 6) + (5z - 2)
-15z + 6 + 5z -2
= -10z + 4
Triangle XYZ is shown on the coordinate plane.
A triangle on the coordinate plane with vertices X at 0 comma 5, Y at 10 comma 3, and Z at 4 comma negative 1.
If triangle XYZ is translated using the rule (x, y) → (x + 2, y + 3) and then reflected across the x-axis to create triangle X″Y″Z″, what is the location of Z″?
(2, −8)
(6, −2)
(8, −2)
(12, −6)
Answers
The transformation of triangle XYZ vertices at X(0, 5), Y(10, 3), and Z(4, -1), indicates that the coordinate of the point Z'' following a composite transformation of a translation of (x, y) → (x + 2, y + 3), and a reflection across the x-axis, is located at the point (6, -2). The correct option is therefore;
(6, -2)What is a reflection transformation?A reflection transformation is a transformation that produces a mirror image of a geometric figure across a line of reflection.
The coordinates of the vertices of the triangle are;
X(0, 5), Y(10, 3), Z(4, -1)
The transformation rule that is used to translate the triangle ΔXYZ (to get ΔX'Y'Z'), can be presented as follows;
(x, y) → (x + 2, y + 3)The reflection of the translated figure of the triangle (ΔX'Y'Z'), to get ΔX''Y''Z'', is a reflection across the x-axis, therefore, we get;
The coordinates of the point (x, y) following a reflection across the x-axis is the point (x, -y)Therefore, we get the coordinate of the point (x, y) following the composite transformation is the point (x + 2, -(y + 3))
(x, -y) → (x + 2, -(y + 3))The coordinates of the point Y(4, -1) following the composite transformation is therefore;
Y(4, -1) → (4 + 2, -(-1 + 3)) = (6, -2)
The correct option is therefore; (6, -2)Learn more on composite transformations here: https://brainly.com/question/18406100
#SPJ1
Share GH$25,000.00 between Amina and Mina in the ratio of 2.3
Answers
Answer:
2x + 3x = $25,000
5x = $25,000
x = $5,000
Amina will receive $10,000, and Mina will receive $15,000.
2:3
First, add 2 and 3 =5
The total money is 5
Then for Amina whose share is 2;
2/5 × 25,000 = GH$10,000.00
For Mina whose share is 3;
3/5 ×25,000 = GH$15,000.00
Therefore
Amina = GH$10,000.00
Mina=GH$15,000.00
Andrea placed $1700 in a savings account compounded monthly at 2.5%. What is the value of her account after 8 years?
Answers
Answer:
Step-by-step explanation:
To calculate the value of Andrea's savings account after 8 years, we need to find the balance after compounding the interest for 96 months (8 years x 12 months per year). We can use the formula for compound interest:
A = P * (1 + r/n)^(nt)
where:
A is the balance after t years,
P is the initial balance ($1700),
r is the annual interest rate (2.5%),
n is the number of times interest is compounded in a year (12),
t is the number of years (8).
Converting the interest rate to a decimal and dividing by the number of times compounded per year:
r/n = 2.5% / 12 = 0.021
Plugging in the values into the formula:
A = 1700 * (1 + 0.021)^(12 * 8) = 1700 * (1.021)^96
Calculating the value:
A = 1700 * 2.8412 = 4860.80
So, the value of Andrea's account after 8 years would be $4860.80.
Please help and explain how you got the answer

Answers
Answer: 30°
Step-by-step explanation:
we have to find the angle adjacent with the right angle. For this we use the (-).
At this point, I am guessing you know how to use SOH-CAH-TOA, for this one we use SOH so sin. If you have a calculator set it on degree mode, then plug it in as sin⁻₁(), we put it like that because the missing angle has the given number opposite and the hypotenuse. It solves it and now we get 30 for the answer. I dont know if that made sense, tell me if it didnt so I can explain it better.
Find the equation of the parabola, the equation of the directrix and the equation of the axis of symmetry

Answers
We know that the focus is at the point F(-5,2); we also know that the directrix of the parabola is eight units to the right of the focus, which means that it passes through the point (3,2) and since it is a vertical line the equation of the directix is:
\(x=3\)The equation of the axis of symmetry in this case must be horizontal and it is given as:
\(y=2\)To find p we first need to find the distance between the two points we discussed earlier, then we will divide by two since the distance between the directix and the focus is twice the value of p. The distance between two poitns is given by:
\(d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)Plugging the values of the points we have:
\(\begin{gathered} d=\sqrt{\left(-5-3\right)^2+\left(2-2\right)^2} \\ d=\sqrt{\left(-8\right)^2+\left(0\right)^2} \\ d=\sqrt{64+0} \\ d=\sqrt{64} \\ d=8 \end{gathered}\)Hence the absolute value of p is:
\(\lvert p\rvert=\frac{8}{2}=4\)Now, since the directix is to the right of the focus this means that the parabola has to open to the left which implies that p has to be negative. Hence:
\(p=-4\)Once we know p we can find the vertex of the parabola. Since the parabola is horizontal and we know it opens to the right we just need to add the absolute value of p to the x-coordinate of the focus, hence we have:
\(V\left(-1,2\right)\)Finally we can find the equation of the parabola:
\(\begin{gathered} x=\frac{1}{4\left(-4\right)}\left(y-2\right)^2+\left(-1\right) \\ x=-\frac{1}{16}\left(y-2\right)^2-1 \end{gathered}\)Therefore, the equation of the parabola is:
\(x=-\frac{1}{16}(y-2)^{2}-1\)The graph of the parabola, axis of symmetry and directrix are shown below:

Please help I am so lost thank you so much

Answers
The speed of the plane is equal to 120 mph.
What is speed?In Mathematics and Geometry, speed is the distance covered by a physical object per unit of time. This ultimately implies that, speed can be measured by using miles per hour (mph).
Mathematically, the speed of any a physical object can be calculated by using this formula;
Speed = distance/time
Time = distance/speed
Let the variable s represent the speed of the plane in miles per hour. Therefore, an equation that models the situation can be written as follows;
240/s = 80/s - 80
80s = 240s - 19200
19200 = 160s
s = 19200/160
s = 120 mph.
Read more on speed here: https://brainly.com/question/29445231
#SPJ1
18x + 3°
( 10x - 27)
Find the measure of each indicated angle
Answers
Answer:
48x-81
Step-by-step explanation:
18x+3(10x-27)
Then distribute
18x+30x-81
Combine like terms
Final Answer: 48x-81
find the greatest possible length which can be used to measure exactly the lengths 4m 95cm; 9m and 16m 65cm?
Answers
Answer: H.C.F. = 32 x 5 = 45. Hence, required length = 45 cm
Step-by-step explanation:
Please help
find All disuntiniteas
Log x + 4x³
——————
X
Answers
I believe the expression you provided is:
(log(x) + 4x^3) / x
To find the discontinuities of this expression, we need to identify any values of x that would cause the expression to be undefined. These values are called the discontinuities.
There are two types of discontinuities to look for:
Removable discontinuities: These occur when a function is undefined at a certain point but can be made continuous by redefining the function at that point.
Non-removable discontinuities: These occur when a function is undefined at a certain point and cannot be made continuous by redefining the function at that point.
To find the discontinuities of the given expression, we need to look for values of x that would make the denominator equal to zero, as this would result in a non-removable discontinuity.
So we solve the equation:
x = 0
This means that x cannot be equal to zero, as it would make the denominator zero and the expression undefined.
Therefore, the only discontinuity of the expression is at x = 0.
Note that there are no removable discontinuities in this expression, as the expression is continuous everywhere except at x = 0.
Please answer this correctly

Answers
Answer: 879.20 km²
Step-by-step explanation:
The diameter of the big circle is 2(10) + 18 = 38
divide the diameter by 2 to get the radius (r) = 19
Area (A) = π·r²
= π(19)²
= 361π
The diameter of the small circle is 18
divide the diameter by 2 to get the radius (r) = 9
Area (A) = π·r²
= π(9)²
= 81π
The area of the shaded region is the difference between the big circle and the small circle.
\(Area_{shaded}=A_{big}-A_{small}\)
= 361π - 81π
= 280π
= 280(3.14)
= 879.20
Answer:
879.20 km²
Step-by-step explanation:
Shaded area= Area of whole circle- area of white circle
Area of circle= πr²
Radius of whole circle= 10+18/2= 19 km
Area of whole circle= 3.14*(19 km)²= 1133.54 km²
Are of white circle= 3.14*(9 km)²= 254.34 km²
Shaded area= 1133.54 km²- 254.34 km²= 879.20 km²
Answer is 879.20 km²
what is the answer to 7=100z
Answers
7/100=100z/100
Simplify
Cancel the terms that are in both The numerator and the denominator
Move the variable to the left
Z=7/100
Answer:
7=100z
We move all terms to the left:
7-(100z)=0
We move all terms containing z to the left, all other terms to the right
-100z=-7
z=-7/-100
z=7/100
Step-by-step explanation:
Fill in the blanks for the explicit formula.
-8, 22, 52, 82, ...
Answers
Answer:
it is 30
Step-by-step explanation:
i took the test so please mark me the brainlest
P(AB)
=
P(A n B)
P(B)
Freshmen
Sophomores
Juniors
Seniors
Boys
3
1
4
2
Girls
7
9
6
5
P(Girl|Senior) =

Answers
P (Girl|Senior) = P(Girl n Senior) / P(Senior)
P(girl n senior) = 5 / 37
P(senior) = 7/37
P(girl | senior) = 5/7
To prepare for his mountain biking trip, Rhyan bought four tire patches. Rhyan paid using a gift card that had $22.20 on it. After the sale, Rhyan’s gift card had $1.90 remaining.
Which equations could you use to find the price of one tire patch? Select all that apply.
4x – 1.9 = 22.2
4x – 22.2 = 1.9
4x + 1.9 = 22.2
4x + 22.2 = –1.9
22.2 – 4x = 1.9
Answers
Answer:
4x + 1.9 = 22.2
22.2 - 4x = 1.9
Step-by-step explanation:
Define the variable:
Let x be the cost of one tire patch (in dollars).Given information:
Number of tire patches purchased = 4Total amount available to spend = $22.20Amount remaining after sale = $1.90First equation
The cost of 4 tire patches and the amount remaining on the gift card equals the total amount on the gift card:
⇒ 4x + $1.90 = $22.20
⇒ 4x + 1.9 = 22.2
Second equation
The total amount on the gift card less the cost of 4 tire patches equals the amount remaining:
⇒ $22.20 - 4x = $1.90
⇒ 22.2 - 4x = 1.9
Answer:
4x + 1.9 = 22.2
22.2 - 4x = 1.9
Step-by-step explanation:
A sequence is defined by f(0) = -20, f(n) = f(n-1) - 5 forn > 1.
1. Explain why f(1) = -20 – 5.
2. Explain why f(3) = -20 – 5 – 5 – 5.
3. Complete the expression: f(10) = -20 –
. Explain your reasoning.
Answers
Answer:
1. Proved down
2. proved down
3. f(10) = -20 - 5 - 5 - 5 - 5 - 5 - 5 - 5 - 5 - 5 - 5
Step-by-step explanation:
Let us explain how to solve the question
∵ f(0) = -20, f(n) = f(n - 1) - 5 for n > 1
→ That means we have an arithmetic sequence with constant
difference -5 and first term -20
1. → f(1) means we need to find the second term, which equal the
term - 5
∵ f(1) means n = 1
∴ f(1) = f(1 - 1) - 5
∴ f(1) = f(0) - 5
∵ f(0) = -20
∴ f(1) = -20 - 5 → Proved
2. → f(3) means we need to find the third term, which equal the
second term - 5
∵ f(3) means n = 3
∴ f(3) = f(3 - 1) - 5
∴ f(3) = f(2) - 5
→ f(2) = f(1) - 5
∵ f(1) = -20 - 5
∴ f(2) = [-20 - 5] - 5 = -20 - 5 - 5
∴ f(3) = [-20 - 5 - 5] - 5
∴ f(3) = -20 - 5 - 5 - 5 → Proved
3. → From 1 and 2 we notice that the number of -5 is equal to n,
at n = 1 there is one (-5), when n= 3 there are three (-5)
∵ n = 10
∴ There are ten (-5)
∴ f(10) = -20 - 5(10)
∴ f(10) = -20 - 5 - 5 - 5 - 5 - 5 - 5 - 5 - 5 - 5 - 5 → Proved
(x-1)(x-3)(x+5)(x+7)=297
Answers
First simplify the expression into polynomial form,
\((x-1)(x-3)(x+5)(x+7)=297\)
\(x^4+8x^3-10x^2-104x+105=297\)
\(x^4+8x^3-10x^2-104x-192=0\)
Now factor into,
\((x-4)(x+8)(x^2+4x+6)=0\)
Which means the solutions are,
\(x-4=0\implies\boxed{x_1=4}\)
\(x+8=0\implies\boxed{x_2=-8}\)
and then two complex solutions because determinant of the third factor \(D\lt0\),
\(x^2+4x+6=0\)
\(x^2+4x+4=-2\)
\((x+2)^2=-2\implies\boxed{x_3=i\sqrt{2}-2},\boxed{x_4=-i\sqrt{2}-2}\)
Hope this helps :)
Answer:
x=4
Step-by-step explanation:
(4-1)(4-3)(4+5)(4+7)=297
Is this answer Correct and if not which one is with a simple Explanation? :)

Answers
SOLUTION:
Outliers are defined as about 1.5 times the interquartile range above the upper quarttile and below the lower quartile (Q1 - 1.5 IQR or Q3 + 1.5 IQR).
\(\begin{gathered} \text{IQR = Q3 - Q1 = 65 - 50 = 15} \\ outlier=Q3+1.5(15) \\ =65+22.5=87.5 \end{gathered}\)Since John's score is 81 which is below 87.5, so John is not an outlier.
If your base pay is 10000 your commission rate is 40% you sell 15 cars and you earn 40000 how much does each car cost
Answers
Answer: $4,000
Step-by-step explanation:
If the total earnings were $40,000 and the base pay was $10,000, then the commission earned would be $40,000 - $10,000 = $30,000.
Since the commission rate is 40%, we can set up the equation:
40% x Total Sales = Commission Earned
We know that the commission earned is $30,000, and we also know that 15 cars were sold. Therefore, we can solve for the average price of each car:
40% x Total Sales = Commission Earned
40% x (15 x Price per Car) = $30,000
6 x Price per Car = $30,000
Price per Car = $5,000
However, this is just the average price per car. Since the commission is based on the total sales, we need to calculate the actual commission earned on each car:
Commission per Car = 40% x Price per Car
Commission per Car = 40% x $5,000
Commission per Car = $2,000
Therefore, the total earnings of $40,000 divided by the number of cars sold (15) gives the amount earned per car:
Amount earned per Car = Total Earnings / Number of Cars Sold
Amount earned per Car = $40,000 / 15
Amount earned per Car = $4,000
Please answer this It would mean alot to me.

Answers
The expression 8x + 4y is not equivalent to 4(2x + 1). Therefore, 8x + 4y = 4(2x + y)
How to find equivalent expression?Two expressions are said to be equivalent if they have the same value irrespective of the value of the variable(s) in them.
Equivalent expressions are expressions that have similar value or worth but do not look the same.
Let's determine whether the expression 8x + 4y is equivalent to 4(2x + 1).
Let's factorise to know whether the expressions are equivalent.
Therefore, using the common factors,
8x + 4y = 4(2x + y)
Hence, the expression are not equivalent .
learn more on equivalent expression here: https://brainly.com/question/28170201
#SPJ1
hello i need help with questions 5 please thank you.

Answers
5a) The total cost of buying the car, priced at $32,000 with the harmonized sales tax (HST) of 13%, is $36,160.
5b) Through the lease, the customer saves $14,760.
5c) The lease options for the lessee after returning the car include:
Lease buyoutLease extensionNew lease contractBuying out the vehicle and then reselling it.6a) The after-tax cost of the Honda Civic is $32,199.35.
6b) The value of the vehicle that needs to be financed is $26,199.35.
6c) The monthly payment will be $567.26 for 4 years.
6d) After four years, the total amount paid for the vehicle is $33,228.48.
Financing Options:A lease is a financing option for the use of capital assets by which the lessee utilizes an asset for a stated period while making periodic payments to the lessor.
A car purchase can also be financed through loans, like home mortgages.
Value of the car = $32,000
Harmonized Sales Tax (HST) = 13%
Cost of the car with HST = $36,160 ($32,000 x 1.13)
Lease Arrangement:Down payment = $1,000
Financing part = $35,160 ($36,160 - $1,000)
Installment payments = 48
Periodic payments = $425
Total lease cost = $21,400 ($1,000 + 48 x $425)
Savings (advantages) from leasing = $14,760 ($36,160 - $21,400)
Jordan's Car:The value of the Honda Civic = $28,495
Harmonized Sales Tax (HST) = 13%
After-tax cost = $32,199.35 ($28,495 x 1.13)
Annual interest rate = 1.9% compounded monthly
Down payment = $6,000
Financing part = $26,199.35 ($32,199.35 -$6,000)
Financing period = 4 years
N (# of periods) = 48 months (4 years x 12)
I/Y (Interest per year) = 1.9%
PV (Present Value) = $26,199.35
FV (Future Value) = $0
P/Y (# of periods per year) = 12
C/Y (# of times interest compound per year) = 12
Results:
Monthly Payments (PMT) = $567.26
Sum of all periodic payments = $27,228.48
Total Interest $1,029.13
Total amount paid over 4 years = $33,228.48 ($27,228.48 + $6,000)
Learn more about Car Financing at https://brainly.com/question/28803707
#SPJ1
Tom earns $12.50 per hour at the Yankee Bowling Alley. He regularly works 40 hours per week. He is paid time and a half for each hour of overtime work. Last week he worked 42 hours. What is his pay for the week?
Answers
Answer:
Tom's pay for the week should be over 500 dollars. Sorry if this isn't very helpful. :(
Step-by-step explanation:
I don’t understand stand this question someone please help me with work shown

Answers
Answer:
8.9 miles
Step-by-step explanation:
well, you got 2 points with their coordinates on the grid if the city. to make it easy, the origin = point (0,0) is also the center of the city.
the school is 4 miles east = 4 units plus to the right in positive x direction.
and 2 miles south = 2 units down in negative y direction.
so, the point school is (4, -2).
the pool is 8 miles east = 8 units plus to the right in positive x direction.
and it is 6 miles north = 6 units up in positive y direction.
so, the point pool is (8, 6).
now we need to find the distance between both points to see how far they need to travel.
just one remark : this is flawed, as we can usually not make a beeline in a city from one place to another. we have to go along streets. but let's ignore that and just find the air distance.
now, to find the direct distance between 2 points, we need Pythagoras for right-angled triangles
c² = a² + b²
c = the Hypotenuse, the baseline opposite of the 90 degree angle. = the direct distance between the 2 points.
a and b are the sides of a right-angled triangle, which are nothing else than the differences of the x and y coordinates of the 2 points.
the x difference between school and pool is 8-4 = 4.
the y difference between school and pool is 6 - -2 = 6 + 2 = 8.
don't worry, if you did it the other way around and got negative numbers. remember that in the Pythagoras formula everything has to be squared first (and that turns also negative numbers into positive ones).
so, we get
c² = 4² + 8² = 16 + 64 = 80
c (the distance) = sqrt(80)
"sqrt" is the usual abbreviation of "square root".
sqrt(80) ≈ 8.9 miles
Don Swifter earns $9.75 per hour as a clerk. He starts work Monday through Friday morning at 8:00 AM. He takes a one-half hour lunch break every day. If he finishes work at 3:30 PM Monday through Thursday, how late must he work on Friday to have total pay of $360.75 for the week?
Answers
Answer:
He works until 5:30.
Step-by-step explanation:
ok so first, every day don would take a total of 7 hours and 30 minutes on mon-Thurs. If we subtract his lunch from that total it would be 7 hours so next we do 7 hours times 9.75 which is 68.25$. Now that we know how much he makes per day, we times that by 4 since mon-thurs is 4 days. This would be 273$. Now we need to get to 360.75 so we subtract that. This would be 87.75$. Now if a normal day is 68.25$ and friday is 87.75, we find the diffrence which is 19.50. which is also 9.75(an hour) x 2 resulting in 2 hours extra. Therefore, he works 9 hours and 30 minutes on fridays (until 5:30). Thanks for putting in the work to understand and have a nice day!
Don must work approximately 9 additional hours on Friday to have a total pay of $360.75 for the week.
How to determine how late he must workDon works from 8:00 AM to 3:30 PM Monday through Thursday. Let's calculate his total work hours for these four days:
Total work hours from Monday to Thursday:
(3:30 PM - 8:00 AM) - 0.5 hours (lunch break)
= 7.5 hours - 0.5 hours
= 7 hours (per day)
Total work hours for the week (Monday to Thursday):
4 days x 7 hours/day = 28 hours
Total pay for the week = Hourly rate x Total work hours + Additional hours on Friday
$360.75 = $9.75 x 28 hours + Additional hours on Friday
Additional hours on Friday = ($360.75 - $9.75 x 28) / $9.75
Additional hours on Friday = ($360.75 - $273) / $9.75
Additional hours on Friday = $87.75 / $9.75
Additional hours on Friday ≈ 9 hours (rounded to the nearest hour)
Learn more about work hours
https://brainly.com/question/3164396
#SPJ3