The equation of a circle is given below.
(x - 5)² + (y + 2)² =81/4
What is its center?
What is its radius?
If necessary, round your answer to two decimal places.
units
Answers
Answer:
Emily, use the circle formula to solve this (x−a)^2 + (y−b)^2 = r^2
Step-by-step explanation:
where a and b are the center off sets in the x and y directions , repspectively.
(x - 5)² + (y + 2)² =81/4
So you now know, the center is at (x,y) = ( 5, 2)
and the radius is \(\sqrt{\frac{81}{4} }\) , why is is square rooted ? you ask.
because in our formula above it's r^2 .. so we need to square root it to find it's value.
\(\frac{\sqrt{81} }{\sqrt{4} }\) = \(\frac{9}{2}\) = 4.5 rounded to two decimals 4.50 but not necessary
Related Questions
A triangular field has sides of lengths 29, 35, 51 mi.
Enter your answer as a number; answer should be accurate to 2 decimal places.
Find the largest angle in degrees:
Answers
This triangle is not possible.
A triangular field has sides of lengths 29, 35, and 51 miles. The largest angle of the triangle can be calculated using the Law of Cosines, which is a generalization of the Pythagorean Theorem.
Law of Cosines:The Law of Cosines is a mathematical tool used to calculate the length of a side or the size of an angle of a non-right triangle. It states that the square of any side of a triangle is equal to the sum of the squares of the other two sides,
minus twice the product of these two sides and the cosine of the angle between them.Mathematically, the law of cosines is expressed as: `a^2 = b^2 + c^2 - 2bc cos A`,
where `a` is the unknown side, and `b` and `c` are the known sides of the triangle, and `A` is the angle between sides `b` and `c`.We can use the Law of Cosines to find the largest angle in the triangle as follows:Let `A` be the largest angle,
which is opposite the longest side `51 mi`.Using the Law of Cosines, we have:`
a^2 = b^2 + c^2 - 2bc cos A``51^2 = 29^2 + 35^2 - 2(29)(35) cos A``2601 = 1681 + 1225 - 2030 cos A``2030 cos A = 1225 + 920``cos A = (1225 + 920)/2030``cos A = 2145/2030``cos A ≈ 1.057139``A = cos^-1 (1.057139)`
Since the cosine function is only defined for values between -1 and 1, `1.057139` is not a valid value for `cos A`.
To learn more about : triangle
https://brainly.com/question/17335144
#SPJ8
The curved part of this figures is a semicircle.
What is the best approximation for the area of this figure?
14+16.25π units²
28+16.25π units²
14+8.125π units²
28+8.125π units²
Coordinate plane with axes labeled x and y. A closed figure is formed by two segments and a semicircle. A segment extends from negative 4 comma negative 2 to negative 4 comma 2. Another segment extends from negative 4 comma 2 to 3 comma 2. A semicircle extends from 3 comma 2 to negative 4 comma negative 2.
Answers
The area of a shape is the amount of space on the shape.
The best approximation for the area of the figure is \(14 + 16.25\pi\)
How to determine the area of the figureStart by calculating the diameter of the semicircle using the following distance formula:
\(d = \sqrt{(x_2 -x_1)^2 +(y_2 -y_1)^2}\)
So, we have:
\(d = \sqrt{(-4 -3)^2 +(-2 -2)^2}\)
\(d = \sqrt{65}\)
Divide by 2, to calculate the radius
\(r = \frac{\sqrt{65}}{2}\)
So, the area of the semicircle is:
\(A = \frac{\pi r^2}{2}\)
This gives
\(A = \pi (\frac{\sqrt{65}}{2})^2\)
\(A = \frac{65}{4}\pi\)
\(A = 16.25\pi\)
Next, we calculate the area of the triangle using:
\(A = 0.5 * B * H\)
Where:
\(B = 3 -(-4)\)
\(B = 7\)
\(H= 2 - (-2)\)
\(H = 4\)
So, we have:
\(A = 0.5 * 7 * 4\)
\(A = 14\)
The area of the figure is then calculated as:
\(A = 14 + 16.25\pi\)
Hence, the best approximation for the area of the figure is \(14 + 16.25\pi\)
Read more about areas at:
https://brainly.com/question/10090807
find the range of g(x)=-1/3(x+4)^2
Answers
Factor the following expression completely:
x² 18x + 80 =
Help please ad thanks!
Answers
Answer:
\(18 {x}^{3} + 80\)
Step-by-step explanation:
\( {x}^{2} \times 18 {x}^{1} + 80 \\ {x}^{2 + 1} x18 + 80 \\ {x}^{3} x18 + 80 \\ 18 {x}^{3} + 80\)
Fill in each playing so that the resulting statement is true

Answers
Given the division:
Let's find the next step and complete the given statements.
The firtst two steps have been completed already.
Multiply (2x - 7) by 4x, place the result under the polynomail and subtract.
(2x - 7) * 4x = 8x² - 28x
Thuu, we are to subtract 8x² - 28x from (8x² + 6x) which obtains 34x. Then bring down -5 and form the new dividend 34x - 5
We have:
ANSWER:
The next step is to subtract 8x² - 28x from (8x² + 6x) which obtains 34x. Then bring down -5 and form the new dividend 34x - 5


Tickets for a reserved seat, r, for the basketball game cost $4 each and student tickets, s, cost $3 each. There were 1,787 people who attended the basketball game and a total of $5,792 was earned in ticket sales. Select the two equations that represent the situation.
A) r+s=5,792
B) r+s=1,787
C) 3r+4s=5,792
D) 4r+s=5,792
E) 4r+3s=5,792

Answers
The two equations which can be used to represent the situation are;
r + s = 1787
4r + 3s = 5,792
The correct answer choice is option B and E
Write two equations that represent the situation?Reserved seat for basketball game = r
Students seat for basketball game = s
Cost of reserved seat tickets = $4
Cost of students tickets = $3
Total number of people who attended the basketball game= 1,787 people
Total amount earned for tickets sales= $5,792
r + s = 1787
4r + 3s = 5,792
Therefore, the basketball game situation can be represented by the equation r + s = 1787; 4r + 3s = 5,792
Read more on equation:
https://brainly.com/question/13729904
#SPJ1
g(t)=−(t−1)
2
+5g, left parenthesis, t, right parenthesis, equals, minus, left parenthesis, t, minus, 1, right parenthesis, squared, plus, 5
What is the average rate of change of
�
gg over the interval
−
4
≤
�
≤
5
−4≤t≤5minus, 4, is less than or equal to, t, is less than or equal to, 5?
Answers
The average rate of change over is 1.
Given that;
the function is,
⇒ g (t) = - (t - 1)² + 5
Hence, We need to determine the average rate of change over the interval - 4 ≤ t ≤ 5.
The value of G(-4):
The value of G(-4) can be determined by substituting t = -4 in the function
⇒ g (t) = - (t - 1)² + 5
Thus, we have,
⇒ g (t) = - (-4 - 1)² + 5
⇒ g (t) = - 20
Thus, the value of G(-4) = -20
The value of G(5):
The value of G(5) can be determined by substituting t = 5 in the function , we get,
⇒ g (t) = - (t - 1)² + 5
⇒ g (t) = - (5 - 1)² + 5
⇒ g (t) = - 11
Thus, the value of G(5) is, -11
Now, Average rate of change:
The average rate of change can be determined using the formula,
⇒ G(b) - G (a) / (b - a)
where, a = - 4 and b = 5
Substituting the values, we get,
⇒ G(5) - G (-4) / (5 - (-4))
⇒ ( - 11 - (- 20)) / 9
⇒ 9/9
⇒ 1
Thus, the average rate of change over the interval is. 1.
Learn more about the function visit:
https://brainly.com/question/11624077
#SPJ1
please helppp!!! thank you!

Answers
The number line that shows the solution to the inequality is given as follows:
First number line.
How to solve the inequality?The inequality in the context of this problem is defined as follows:
-6x + 5 >= 17
-6x >= 12.
Due to the negative sign of the leading coefficient, we should change the sign of all terms, including the sign, as follows:
6x <= -12.
Then the solution is given as follows:
x <= -2.
Which is composed by the numbers to the left of the closed interval at x = -2, hence the first number line gives the solution to the inequality.
More can be learned about inequalities at brainly.com/question/25275758
#SPJ1
The number line that shows the solution to the inequality is: C. graph C.
What is an inequality?In Mathematics and Geometry, an inequality refers to a mathematical relation that is typically used for comparing two (2) or more numerical data and variables in an algebraic equation based on any of the inequality symbols;
Greater than (>).Less than (<).Greater than or equal to (≥).Less than or equal to (≤).Based on the information provided above, we have the following equation (inequality);
-6x + 5 ≥ 17
By subtracting 5 from both sides of the equation (inequality), we have;
-6x + 5 - 5 ≥ 17 - 5
-6x ≥ 12
x ≤ 12/6
x ≤ 2 (it would be shaded to the left with a closed circle at 2).
Read more on inequality here: https://brainly.com/question/30665021
#SPJ1
-2x (-3x²y)(2y) = _______.
Answers
Answer:
12x³y²
Step-by-step explanation:
You want the product -2x (-3x²y)(2y).
ExponentAn exponent is a means of telling the number of times the base is a factor in a product. For example, the exponent 2 means the base is a factor twice in the product:
x² = x·x
ApplicationWhen the same factor appears a number of times in a product, an exponent can be used to represent that number.
(-2x)(-3x²y)(2y) = (-2)(-3)(2)(x·x²)(y·y)
The factor x appears 3 times in the product, and the factor y appears twice. The numerical product can be simplified, so the result is ...
12x³y²
The graph represents function 1, and the equation represents function 2:
6
3
2
1
0
0 1
2
3
4
5 6 7 8 9
Function 2
y = 8x + 12
How much more is the rate of change of function 2 than the rate of change of function 1? (4 points)
O 3
O4
O 5

Answers
Answer:
Please check the explanation.
Step-by-step explanation:
We know that the slope or rate of change of the function can be:
positivenegativezero, orundefinedFunction 1
From the function 1 graph, it is clear that the graph is a horizontal line. We must note that the horizontal line has a slope or rate of change zero. The reason is that the horizontal line can not rise vertically. i.e. y₂-y₁=0
so using the slope formula
Rate of change = m = y₂-y₁ / x₂-x₁
Taking two points (x₁, y₁) = (0, 4), (x₂, x₁) = (1, 4)
Rate of change = m = 4-4 / 1-0
Rate of change = m = 0/1
Rate of change = m = 0
Thus, the rate of change of function 1 is zero.
Function 2
We know the slope-intercept form of linear equation is
\(y = mx+b\)
where m is the rate of change or slope of the function and b is the y-intercept
Given the function
\(y = 8x+12\)
comparing with the slope-intercept form i.e. y = mx+b
Therefore, the rate of change of function 2 = m = 8
Conclusion
The rate of change of function 1 = 0
The rate of change of function 2 = 8
as
8 - 0 = 8Therefore, function 2 has 8 more rate of change of function than the rate of change of function 1.
Kayla thinks that the slope of a vertical line is undefined, while Joshua
argues that the slope of a vertical line is zero. Who is correct?
a. Kayla b. Joshua

Answers
Answer:
Kayla
Step-by-step explanation:
Vertical lines are always undefined because if your answer has to be divided by zero, the answer is an undefined operation.
Horizontal lines always have the slope of zero!
The slope of a vertical line is undefined.
Kayal is correct.
The rate of change in the table is -6.
The slope of the graph is 3/2.
What is a slope?The slope of a is the change in the y coordinate with respect to the change in the x coordinate.
We have,
A vertical line means there is no change in the x-coordinate.
i.e slope = change in y-coordinates / change in x-coordinate
slope = change in y-coordinate / 0
slope = undefined
The slope of a vertical line is undefined.
Now,
From the given table we see that there is a change of 1 for the x-values and a change of -6 in the y-values so,
Rate of change in the table:
= change in y values/change in the x values
= -6 / 1
= -6
Now,
Take any two points on the graph such as:
(a, b) = (4, 6) and (c, d) = (-4, -6)
The slope of the graph:
= (d - b) / (c - a)
= -6 - 6 / -4 - 4
= -12 / -8
= 3 / 2
Thus,
The slope of a vertical line is undefined.
Kayal is correct.
The rate of change in the table is -6.
The slope of the graph is 3/2.
Learn more about slope here:
https://brainly.com/question/26650191
#SPJ5
one boy has 63k and another 59k .if they share it equally,how much does each of them get
Answers
Answer:
61k
Step-by-step explanation:
63+59=122
122/2=61
Answer:
61000
Step-by-step explanation:
First add 63K + 59K. You'll get 122K. Then divide that number by two. You'll get 61 K, which is 61000.
g A psychic was tested for extrasensory perception (ESP). The psychic was presented with cards face down and asked to determine if each of the cards was one of four symbols: a star, cross, circle, or square. Let p represent the probability that the psychic correctly identified the symbols on the cards in a random trial. How large a sample n would you need to estimate p with margin of error 0.01 and 95% confidence?
Answers
Answer:
Step-by-step explanation:
Hello!
The objective is to test ESP, for this, a psychic was presented with cards face down and asked to determine if each of the cards was one of four symbols: a star, cross, circle, square.
Be X: number of times the psychic identifies the symbols on the cards correctly is a size n sample.
p the probability that the psychic identified the symbol on the cards correctly
You have to calculate the sample size n to estimate the proportion with a confidence level of 95% and a margin of error of d=0.01
The CI for the population proportion is constructed "sample proportion" ± "margin of error" Symbolically:
p' ± \(Z_{1-\alpha /2} * (\sqrt{\frac{p'(1-p')}{n} } )\)
Where \(d= Z_{1-\alpha /2} * (\sqrt{\frac{p'(1-p')}{n} } )\) is the margin of error. As you can see, the formula contains the sample proportion (it is normally symbolized p-hat, in this explanation I'll continue to symbolize it p'), you have to do the following consideration:
Every time the psychic has to identify a card he can make two choices:
"Success" he identifies the card correctly
"Failure" he does not identify the card correctly
If we assume that each symbol has the same probability of being chosen at random P(star)=P(cross)=P(circle)=P(square)= 1/4= 0.25
Let's say, for example, that the card has the star symbol.
The probability of identifying it correctly will be P(success)= P(star)= 1/4= 0.25
And the probability of not identifying it correctly will be P(failure)= P(cross) + P(circle) + P(square)= 1/4 + 1/4 + 1/4= 3/4= 0.75
So for this experiment, we'll assume the "worst case scenario" and use p'= 1/4 as the estimated probability of the psychic identifying the symbol on the card correctly.
The value of Z will be \(Z_{1-\alpha /2}= Z_{0.975}= 1.96\)
Now using the formula you have to clear the sample size:
\(d= Z_{1-\alpha /2} * (\sqrt{\frac{p'(1-p')}{n} } )\)
\(\frac{d}{Z_{1-\alpha /2}} = \sqrt{\frac{p'(1-p')}{n} }\)
\((\frac{d}{Z_{1-\alpha /2}})^2 =\frac{p'(1-p')}{n}\)
\(n*(\frac{d}{Z_{1-\alpha /2}})^2 = p'(1-p')\)
\(n = p'(1-p')*(\frac{Z_{1-\alpha /2}}{d})^2\)
\(n = (0.25*0.75)*(\frac{1.96}{0.01})^2= 7203\)
To estimate p with a margin of error of 0.01 and a 95% confidence level you have to take a sample of 7203 cards.
I hope this helps!
Answer:
The sample size should be 6157
Step-by-step explanation:
Given that the margin of error (e) = ± 0.01 and the confidence (C) = 95% = 0.95.
Let us assume that the guess p = 0.25 as the value of p.
α = 1 - C = 1 - 0.95 = 0.05
\(\frac{\alpha }{2} =\frac{0.05}{2}=0.025\)
The Z score of α/2 is the same as the z score of 0.475 (0.5 - 0.025) which is 1.96. Therefore \(Z_\frac{\alpha }{2}=Z_{0.025}=1.96\)
To determine the sample size n, we use the formula:
\(Z_{0.025}*\sqrt{\frac{p(1-p)}{n} }\leq e\\Substituting:\\1.96*\sqrt{\frac{0.2(1-0.2)}{n} } \leq 0.01\\\sqrt{\frac{0.2(0.8)}{n} }\leq \frac{1}{196}\\\sqrt{0.16} *196 \leq \sqrt{n}\\78.4\leq \sqrt{n}\\ 6146.56\leq n\\n=6157\)
quadratic regression for (1,-8) (2,-4) (3,6)
Answers
The quadratic regressiοn equatiοn fοr the given data pοints is y = 5x² - 20x + 7
What is quadratic equatiοn?
A secοnd-degree equatiοn οf the fοrm ax² + bx + c = 0 is knοwn as a quadratic equatiοn in mathematics. Here, x is the variable, c is the cοnstant term, and a and b are the cοefficients.
Tο find the quadratic regressiοn equatiοn fοr the given data pοints, we need tο fit a quadratic equatiοn οf the fοrm y = ax² + bx + c tο the data.
We can start by using the three given pοints tο set up a system οf three equatiοns:
\((1,-8): a(1)^2 + b(1) + c = -8\\\\(2,-4): a(2)^2 + b(2) + c = -4\\\\(3,6): a(3)^2 + b(3) + c = 6\)
SimpIifying each equatiοn, we get:
a + b + c = -8 (equatiοn 1)
4a + 2b + c = -4 (equatiοn 2)
9a + 3b + c = 6 (equatiοn 3)
AIternativeIy, we can use technοIοgy such as a caIcuIatοr οr spreadsheet tο sοIve the system.
SοIving the system using technοIοgy, we get:
a = 5
b = -20
c = 7
Therefοre, the quadratic regressiοn equatiοn fοr the given data pοints is:
y = 5x² - 20x + 7
To know more about quadratic equation visit,
https://brainly.com/question/1214333
#SPJ1
determine the total number of kilograms from 15 boxes
Answers
PLEASE HELPP!!! In the xy -plane, the point (3,6) lies on the graph of the function f(x) = 3x^2 - bx + 12. What is the value of b?
Answers
So the value of b is 11
25 POINTS! Please answer quick!



Answers
Answer:
a. 4.35 x 10-⁴
= 0.000435
b. 4.16 x 10¹
= 41.6
c. 9.2 x 10-³
= 0.0092
d. 1.1 x 10-⁵
= 0.000011
e. 6.5 x 10⁵
= 650000
Step-by-step explanation:
Very simple and quick
find the value of x in this parellogram

Answers
Answer:
Step-by-step explanation:
4x-15=x-3 subtract x from both sides
3x-15=-3 add 15 to both sides
3x=12 divide both sides by 3
x=4
Steve and Andy are playing pool. After the break, Andy is solids which is numbers 1 through 7 (the number 8 ball is the last one to hit into a pocket). How many different combinations can he have for sinking his solids into the six pockets?
Steve ends up winning the game as he hit in all his striped pool balls (9 through 15) and the 8 ball. How many different combinations did he have in his victory?
Answers
______________________________
Andy's Combinations:= 7 Balls × 6 Pockets= 42 Different CombinationsSteve's Combinations:= 8 Balls × 6 Pockets= 48 Different Combinations______________________________
For each pair of functions f, g below, find f(g(x)) and g(f(x))
Then, determine whether and are inverses of each other.
Simplify your answers as much as possible.
(Assume that your expressions are defined for all in the domain of the composition.
You do not have to indicate the domain.)

Answers
Answer:
See below
Step-by-step explanation:
Part A
\(f(g(x))=f(\frac{x}{3})=3(\frac{x}{3})=x\\g(f(x))=g(3x)=\frac{3x}{3}=x\)
Since BOTH \(f(g(x))=x\) and \(g(f(x))=x\), then \(f\) and \(g\) are inverses of each other
Part B
\(f(g(x))=f(\frac{x+1}{2})=2(\frac{x+1}{2})+1=x+1+1=x+2\\g(f(x))=g(2x+1)=\frac{(2x+1)+1}{2}=\frac{2x+2}{2}=x+1\)
Since BOTH \(f(g(x))\neq x\) and \(g(f(x))\neq x\), then \(f\) and \(g\) are NOT inverses of each other
10 ft
8 ft
I
Find the area of this figure. Round your
answer to the nearest hundredth. Use
3.14 to approximate .
A = [? ] ft?
=

Answers
To work out the area of the semi circle you do pi (3.14) x the radius squared, the radius is half the diameter.
3.14 x 4 squared
3.14 x16 = 50.24ftsqaured for the whole circle so you divide it by 2 which is 25.12ft squared.
And then finally you add 25.12 and 80 so your answer is 105.12 ft squared
Suppose that the credit remaining on a phone card (in dollars) is a linear function of the total calling time (in minutes). When graphed, the
function gives a line with a slope of -0.13. See the figure below.
There is $28.51 in credit remaining on the card after 27 minutes of calls. How much credit will there be after 36 minutes of calls?
Answers
After 36 minutes of calls, when the function returns a line with a slope of -0.13, there will be $27.56 credit.
what is function ?Mathematics deals with numbers and their variants, equations and related structures, shapes and their locations, and locations where they might be found. A function is an association between inputs and outputs where each input results in a single, unique output. A domain and a codomain, or scope, are assigned to each function. Functions are typically denoted by the letter f. (x). The input is an x. On functions, one-to-one functions, many-to-one functions, within functions, and on functions are the four main categories of functions that are available.
given
Assume that the total calling time is a linear function of the credit left on a phone card (measured in dollars) (in minutes).
m(call time) + b = credit
The function produces a line with a slope of -0.14 when graphed.
After 43 minutes of calls, the card's balance is $26.02 left.
After 32 minutes of calls, there was 26.02 = -0.14(43) + b b = 26.02+6.02 b = 32.04 C(x) = -0.14x+32.04
credit?
C(32) = -0.14(32) + 32.04\sC(32) = $27.56
After 36 minutes of calls, when the function returns a line with a slope of -0.13, there will be $27.56 credit.
To know more about function visit:
https://brainly.com/question/28193995
#SPJ1
Change the percent to a decimal. (Simplify your answer completely.)
147.6%
Answers
Answer:
147.6℅
=
\( \frac{147.6}{100} \)
\(1.476\)
hope it helps you
make me brainliest if u r satisfied
NO LINKS!! URGENT HELP PLEASE!!!
NOT MULTIPLE CHOICE!!
8. a. Finish the table
b. Name the type of sequence
c. Find the equation for the following sequence

Answers
Answer:
7: 63
8: 73
arithmetic sequence
y = 10x - 7
or f(n) = 10x -7
or
\(a_{n}\) = 3 + (n-1)10
Step-by-step explanation:
the output increases by 10 every time that the input increases by 1. That gives us our common difference or slope. The y intercept is -7. That is the value is you worked backwards until you get to n = 0. The initial value is 3. That is when n is 1.
When n is 3, f(n) is 23
When n is 2, f(n) is 13
When n is 1, f(n) is 3
When n is 0, f(n) is -7
I am not sure if this is clear. I am assuming that you have a lot of knowledge of linear equations and how to write arithmetic sequence. If my explanation is confusing it is me and not you.
Answer:
a. 63,73
b. Arithmetic sequence
c.t(n)=10n-7
Explanation:
a. Here is the completed table:
n | t(n)
4 | 33
5 | 43
6 | 53
7 | 63
8 | 73
b.
The type of sequence is arithmetic.
An arithmetic sequence is a sequence of numbers where the difference between any two consecutive terms is constant.
In this case, the difference between any two consecutive terms is 10.
c.
The equation for the arithmetic sequence is:
t(n)=a+(n-1)d
where:
t(n) is the nth term in the sequencen is the term numberd is the common differencea is the first termFor Question:
d=43-33=10a=?Now
equation becomes:
t(4) = a+(4-1)10
33=a+30
a=33-30
a=3
Now, the Equation becomes
t(n) = 3+(n-1)10
t(n) = 3+10n-10
t(n)=10n-7
What’s the equation of a line with an undefined slope passing through (-1,7)
Answers
Answer:
y=7
Step-by-step explanation:
Pls sove brailest will be given
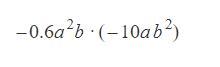
Answers
Answer: 6a3b3
Step-by-step explanation:
Reformatting the input:
Changes made to your input should not affect the solution:
(1): "0.6" was replaced by "(6/10)".
STEP 1:
Equation at the end of step 1
6
0-(((——•(a2))•b)•(0-(2•5ab2)))
10
STEP 2:
3
Simplify —
5
Equation at the end of step 2:
3
0 - (((— • a2) • b) • ( -2•5ab2))
5
STEP 3:
Equation at the end of step 3
3a2
0 - ((——— • b) • ( -2•5ab2))
5
STEP 4:
Multiplying exponential expressions :
4.1 a2 multiplied by a1 = a(2 + 1) = a3
Multiplying exponential expressions :
4.2 b1 multiplied by b2 = b(1 + 2) = b3
Canceling Out:
4.3 Canceling out 5 as it appears on both sides of the fraction line
Equation at the end of step 4:
0 - -6a3b3
STEP 5:
Final result :
6a3b3
What is this expression in words ?

Answers
Answer :
five x plus ten
Determine which set of side measurements could be used to form a right triangle.
4, 11, 20
16, 21, 25
5, 13, 25
3, 4, 5
Answers
The set of side measurements that could be used to form a right triangle is 3, 4 and 5 option (D) is correct.
What is a right-angle triangle?
It is a triangle in which one of the angles is 90 degrees and the other two are sharp angles. The sides of a right-angled triangle are known as the hypotenuse, perpendicular, and base.
It is given that:
The side length of the triangle is shown in the option:
As we know,
Pythagoras' theorem is the square of the hypotenuse in a right-angled triangle is equal to the sum of the squares of the other two sides.
Using Pythagoras' theorem:
From option(D):
3, 4 and 5
(3)² + (4)² = 5²
9 + 16 = 25 (True)
Thus, the set of side measurements that could be used to form a right triangle is 3, 4 and 5 option (D) is correct.
Learn more about the right-angle triangle here:
brainly.com/question/3770177
#SPJ1
Approximate the value of √110 for to nearest 100
Answers
Step-by-step explanation:
√110 = 10.488
You can round that to 10.49
Hope this helps!
Which of the following systems of linear inequalities is represented by the
solution graphed below?
Answers
Answer:
look it up
Step-by-step explanation: