The coordinates given here are three more attractions and their locations
• Aquarium: (-4,1)
Music Hall of Fame: (2,3)
• Lighthouse (-4,-6)
Wesley will bike on the streets. Select all of the route plans that would require Wesley to bike at least 9 miles
Ferris Wheel to Lighthouse to Bridge
O Music Hall of Fame to Art Museum to Ferris Wheel
Aquarium to Bridge to Lighthouse
Aquarium to Art Museum to Music Hall of Fame
O Bridge to Aquarium to Art Museum
Answers
The route plans that would require Wesley to bike at least 9 miles
Ferris Wheel to Lighthouse to BridgeAquarium to Bridge to LighthouseBridge to Aquarium to Art MuseumHow to explain the routeFerris Wheel to Lighthouse to Bridge:
The distance from the Ferris Wheel to the Lighthouse is calculated as sqrt((-4-2)^2 + (1-3)^2) = sqrt(36 + 4) = sqrt(40), which equates to approximately 6.32 miles. Likewise, the distance between the Lighthouse and Bridge are estimated as sqrt((-4-0)^2 + (-6-0)^2) = sqrt(16 + 36) = sqrt(52) or roughly 7.21 miles. Thus, the total calculated mileage is 6.32 + 7.21 and amounts to a total of 13.53 miles.
Music Hall of Fame to Art Museum to Ferris Wheel:
The computation for the span between the Music Hall of Fame and Art Museum is computed by sqrt((2-0)² + (3-6)²) = sqrt(4 + 9) = sqrt(13) or around 3.61 miles. Moreover, the space from the Art Museum to Ferris Wheel determines equal to sqrt((0-(-4))^2 + (6-1)^2) = sqrt(16 + 25) = sqrt(41) amounting to about 6.40 miles. Therefore, summing up the calculflation, we receive a comparable 10.01 miles.
Learn more about coordinate on
https://brainly.com/question/17206319
#SPJ1
Related Questions
Suppose that ƒ is a function given as f(x) = 4x² + 5x + 3.
Simplify the expression f(x + h).
f(x + h)
Simplify the difference quotient,
ƒ(x + h) − ƒ(x)
h
=
Submit Question
The derivative of the function at x is the limit of the difference quotient as h approaches zero.
f(x+h)-f(x)
f'(x) =lim
h→0
h
ƒ(x + h) − f(x)
h
=

Answers
Answer:
f(x +h) = 4x² +4h² +8xh +5x +5h +3
(f(x+h) -f(x))/h = 4h +8x +5
f'(x) = 8x +5
Step-by-step explanation:
For f(x) = 4x² +5x +3, you want the simplified expression f(x+h), the difference quotient (f(x+h) -f(x))/h, and the value of that at h=0.
F(x+h)Put (x+h) where h is in the function, and simplify:
f(x+h) = 4(x+h)² +5(x+h) +3
= 4(x² +2xh +h²) +5x +5h +3
f(x +h) = 4x² +4h² +8xh +5x +5h +3
Difference quotientThe difference quotient is ...
(f(x+h) -f(x))/h = ((4x² +4h² +8xh +5x +5h +3) - (4x² +5x +3))/h
= (4h² +8xh +5h)/h
(f(x+h) -f(x))/h = 4h +8x +5
LimitWhen h=0, the value of this is ...
f'(x) = 4·0 +8x +5
f'(x) = 8x +5
__
Additional comment
Technically, the difference quotient is undefined at h=0, because h is in the denominator, and we cannot divide by 0. The limit as h→0 will be the value of the simplified rational expression that has h canceled from every term of the difference. This will always be the case for difference quotients for polynomial functions.
<95141404393>

TRUE/FALSE. When selecting an alpha level to conduct a hypothesis test, the researcher is determining the probability of making a Type I error.
Answers
If the null hypothesis is correct, the probability that the test will result in a type 1 mistake is what is known as the alpha level for a hypothesis test. In other words, even in the absence of a treatment effect, the alpha level impacts the likelihood of collecting sample data in the critical zone.
The alpha level establishes the boundaries for identifying the key area that results in "extremely unlikely" or significant results that deviate from the null hypothesis. The likelihood of making a Type I error is one in twenty, according to researchers who use an alpha value or level of significance of.05.
The chance of rejecting the null hypothesis when it is true is known as the significance level, which is alternatively written as alpha or. For instance, a significance level of 0.05 represents a 5% probability of assuming the existence of a difference when none actually exists.
Hence we get the required answer.
Learn more about Hypothesis here:
brainly.com/question/15980493
#SPJ4
What is the domain of f(x) = 2|x - 3| + 1 ?
Answers
Domain: all reals, (-∝, ∝)
All inputs for x result in a solution.
S vi) The temperature in Gulmerg in Kashmir was-10°C in January and it rose by 44°c to reach the maximum temperature during summer. The maximum temperature during summer in that year was
Answers
The maximum temperature during summer in that year was 34°C.
It's not possible for the maximum temperature in Gulmarg, Kashmir to rise by 44°C during the summer.
A temperature rise of that magnitude would be extremely unusual and potentially dangerous.
However, assuming that the question meant to ask about the difference between the minimum temperature in January and the maximum temperature in summer, we can proceed with the calculation.
The minimum temperature in January was -10°C, and if we add 44°C to it, we get:
-10°C + 44°C = 34°C
Therefore, the maximum temperature during summer in that year was 34°C.
for such more question on temperature
https://brainly.com/question/14820864
#SPJ11
check whether the given value of x in the solution to the equation.

Answers
Answer: Yes
Step-by-step explanation: Here, we want to decide
if 2 is a solution for the equation 4n - 3 = -2n + 9.
We can do this by simply plugging in 2 for n.
If the statement holds true, then 2 is a solution.
Plugging in 2 for n, we have 4(2) - 3 = -2(2) + 9.
Remember that a negative times a positive is a negative.
So we have 8 - 3 = -4 + 9.
Simplifying further, we have 5 = 5.
Notice that 5 = 5 is a true statement.
So yes, 2 is a solution for the equation 4n - 3 = -2n + 9.
The pair of points (5, 6) and (10, y) lie on a line with a slope of 4/5. Set up and solve for the missing y-value using the slope formula. Show all work.
Answers
Answer:
y = 10
Step-by-step explanation:
calculate the slope m of the 2 points using the slope formula and equate to the given slope.
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (5, 6 ) and (x₂, y₂ ) = (10, y )
m = \(\frac{y-6}{10-5}\) = \(\frac{y-6}{5}\)
equate this expression for m to the given m of \(\frac{4}{5}\)
\(\frac{y-6}{5}\) = \(\frac{4}{5}\) ( cross- multiply )
5(y - 6) = 20 ( divide both sides by 5 )
y - 6 = 4 ( add 6 to both sides )
y = 10
The graph of Fx), shown below, has the same shape as the graph ofG(x) = x?, but it is shifted down 3 units. What is its equation?F(x) =O A. F(X) = (x+3)B. F(x) = x3-3O.C. F(x) = (x-3)D. Fx) = x3 + 3
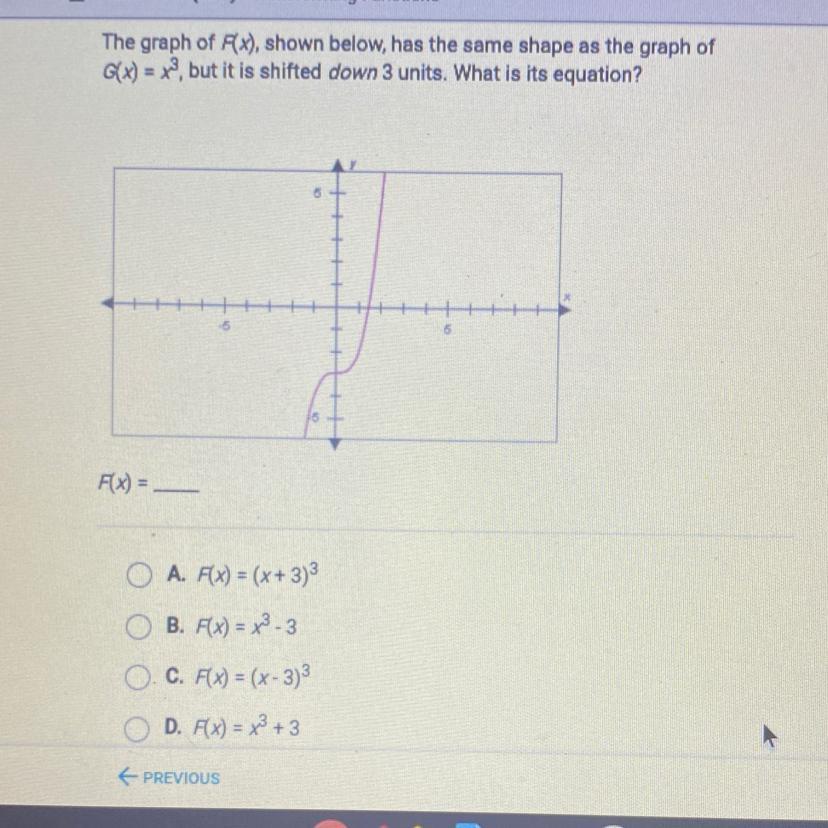
Answers
The correct answer is option B
That is
\(f(x)=x^3-3\)how do i do linear functions?
Answers
Answer:
1. Substitute the value of f(x) into the problem. 8=3x-1.
2. Isolate the variable. Add 1 to both sides to isolate the variable term by using the opposite operation to move the constant term across the equal sign. ...
3. Continue to isolate the variable. ...
4. Simplify.
Step-by-step explanation:
can someone help with my question ill give you brainist or whatever lol

Answers
Answer: 95
Step-by-step explanation:
The easiest way to solve this problem is to solve for each of the triangles:
(formula: B*H/2) 10*3/2 + 10*16/2
15+80
95
---------{NOTICE}----------
If you have any additional questions the best way to reach me is via discord
user: michaelsaltandpepper#9640
What is Seventeen and four hundred six ten thousandths as a decimal
Answers
Answer:17.416
Step-by-step explanation:
I think you misspelled teen as ten so if so, this is the answer.
The fracture strength of tempered glass averages 14 (measured in thousands of pounds per square inch) and has standard deviation 2. (a) What is the probability that the average fracture strength of 100 randomly selected pieces of this glass exceeds 14.2
Answers
Answer:
0.1587 = 15.87% probability that the average fracture strength of 100 randomly selected pieces of this glass exceeds 14.2.
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
The fracture strength of tempered glass averages 14 (measured in thousands of pounds per square inch) and has standard deviation 2.
This means that \(\mu = 14, \sigma = 2\)
Sample of 100:
This means that \(n = 100, s = \frac{2}{\sqrt{100}} = 0.2\)
What is the probability that the average fracture strength of 100 randomly selected pieces of this glass exceeds 14.2?
This is 1 subtracted by the p-value of Z when X = 14.2. So
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{14.2 - 14}{0.2}\)
\(Z = 1\)
\(Z = 1\) has a p-value of 0.8413.
1 - 0.8413 = 0.1587
0.1587 = 15.87% probability that the average fracture strength of 100 randomly selected pieces of this glass exceeds 14.2.
can you show how to find the solution of number 11 on a unit circle

Answers
Solution
Explanation:
Apply the reference angle by finding the angle with equivalent trig values in the first quadrant. Make the expression negative because cosine is negative in the second quadrant.
\(cos\frac{-3\pi}{4}\)Use the following property
\(cos(-x)=-cosx\)\(\begin{gathered} cos(-\frac{3\pi}{4})=-cos\frac{3\pi}{4} \\ =-\frac{\sqrt{2}}{2} \end{gathered}\)Therefore the value of cosine in the second quadrant is negative
Then, cos (-3π/4) =
\(-\frac{\sqrt{2}}{2}\)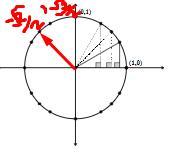
A survey team is trying to estimate the height of a mountain above a level plain. From one point on the plain, they observe that the angle of elevation to the top of the mountain is 32 ∘ . From a point 2000 feet closer to the mountain along the plain, they find that the angle of elevation is 34 ∘ . How high (in feet) is the mountain?
Answers
Answer: 3528.25
Step-by-step explanation:Make a sideview sketch
you should have 2 triangles, one right-angled containing the height and a scalene triangle with angles 24° , 153° (the supplement of 27°) and 3°
the side opposite the 3° angle is 1000
by let the side opposite the 24° be x, (also the hypotenuse of the right-angled triangle)
x/sin24 = 1000/sin3
x = 1000sin24/sin3
let the height of the mountain be h
sin 27 = h/x
h = x sin27 = (1000sin24/sin3)(sin27)
= 3528.25
Joe is asked to prove that the sum of the interior angles (, , and ) of the triangle he has drawn equals 180°. His triangle is represented in the diagram above, and his work is shown below.
Answers
The angles <1, <2, and <3 will not add up to 180 degrees. The angles <1 and <2 are alternate interior angles, and the angles <2 and <3 are also alternate interior angles, AB is parallel to CD.
What is angle sum property of triangle?The angle sum property of a triangle states that the sum of the interior angles of a triangle is always equal to 180 degrees. This means that if you measure the angles inside any triangle and add them up, the result will always be 180 degrees. This property holds true for all types of triangles, whether they are equilateral, isosceles, or scalene.
To understand this property, consider a triangle ABC with interior angles angle A, angle B, and angle C. If we draw a line segment from vertex A to a point D on side BC such that it is parallel to the side AB, then we can see that angle A and angle C are alternate interior angles of the parallel lines AB and CD. Similarly, angle B and angle C are alternate interior angles of the parallel lines BC and AD.
To know more about isosceles, visit:
https://brainly.com/question/9872652
#SPJ1

Probability Math Question
Help would be appreciated:))

Answers
Answer:
Hi, your answer here would be based on reading this graph. For question a, there are a total of 12 people who like vanilla with sprinkles, which means that it is 12 out of 24 or 1/2 or 0.5 or 50 percent.
For b) there is a total of 9 for chocolate, so the probability is 9 out of 24 or 37.5 percent or 3/8 or 0.375
For c) there are a total of 6 with no sprinkles out of 24 so it is 1/4 or 0.25 or 25 percent.
Step-by-step explanation:
Please mark me as brainliest :)
A square-shaped warehouse has a floor area of 12,769 square feet. The length of one of the walls is ___ feet.
Select one:
a. 100
b. 23.37
c. 127.69
d. 113
e. none of these
Answers
Answer:
113 (d)
Step-by-step explanation:
Since the room is square-shaped, you square root the area (12,769) to find the length of each wall. You will get the answer 113. To check this answer multiply 113 by 113 and make sure you get the correct area; it works, so you know the answer is D.
Item 3 Find the distance from the point (-2,6) to the line y=x-8 . Round your answer to the nearest tenth
Answers
Answer:
16 units
Step-by-step explanation:
The distance of the point P ( -2 , 6 ) to the line y = x - 8 is given by the equation D = 8√2 units = 11.3 units
What is the distance from the point to a line?The shortest distance between any two points on an infinite straight line is called the distance from a point to a line. The length of the line segment connecting the point to the closest point on the line is the perpendicular distance between the point and the line.
Let the equation of line be = Ax + By + C = 0
Let the point be P ( x₀ , y₀ )
Distance of a point to line D = | Ax₀ + By₀ + C | / √ ( A² + B² )
Given data ,
Let the distance be represented as D
Now , let the point be P = P ( -2 , 6 )
Let the equation of line be A
The value of A is
y = x - 8
Subtracting y on both sides of the equation , we get
x - y - 8 = 0 be equation (1)
Now , Distance from a point to line D = | Ax₀ + By₀ + C | / √ ( A² + B² )
Substituting the values in the equation , we get
Distance from a point to line D = | 1 ( -2 ) + ( -1 ) ( 6 ) - 8 | / √ ( 1² + 1² )
On simplifying the equation , we get
Distance from a point to line D = | -2 - 6 - 8 | / √2
Distance from a point to line D = | -16 | / √2
Distance from a point to line D = 16/√2
Multiply the numerator and denominator of the fraction by √2 , we get
Distance from a point to line D = 16√2 / 2
Distance from a point to line D = 8√2 units
Hence , the distance is 8√2 units = 11.3 units
To learn more about distance from a point to line click :
https://brainly.com/question/21096072
#SPJ2
Please help on this math question!!!

Answers
The height, above the ground, of a block on a vertical spring is a sinusoidal (trigonometric) function of time. In the interval from time 2.1 seconds to time 2.7 seconds, the block's height decreases from its maximum of 48 inches to its minimum of 30 inches. Which function h(t) could model the block's height in inches above the ground at time t seconds?
Answers
The cosine function that could model the block's height in inches above the ground at time t seconds is:
h(t) = 9cos(1.67π(x - 2.1)) + 39.
What is the cosine function?The cosine function is defined as follows:
g(x) = acos(bx+c)+d.
The coefficients have these following roles:
a: amplitude.b: The period is of 2pi/B.c: phase shift.d: vertical shift.In this problem, we have that the maximum value is of 48 and the minimum value is of 30(difference of 18), hence the amplitude is given as follows:
2a = 18
a = 9.
A standard cosine function with amplitude 9 would vary the between -9 and 9, while this one varies between 30 and 48, hence the vertical shift is of d = 39.
The minimum and maximum values form half the period, hence:
π/B = 2.7 - 2.1
B = π/0.6
B = 1.67π.
The maximum value in the standard function is at x = 0, while at this function is at x = 2.1, hence the phase shift is of 2.1 units to the right, that is, c = -2.1.
Hence the cosine function is:
h(t) = 9cos(1.67π(x - 2.1)) + 39.
This function is graphed at the end of the answer, showing that the minimum and the maximum values are as desired.
More can be learned about cosine functions at brainly.com/question/21558626
#SPJ1

The volume of a chocolate box is given by the formula
V=1 xw x h. Find the width of the chocolate box if
V = 100, 1 = 5, and h = 2.5.
W =?
Answers
Answer:
8 unitsStep-by-step explanation:
Given Formula:
V = L x W x HSolution:
100 = 5 x W x 2.5=> 100 = 12.5 x W=> 2 x 100 = 12.5W x 2=> 200 = 25W=> W = 200/25=> W = 8Hence, the width of the chocolate box is 8 units.
Answer:
W = 8
Step-by-step explanation:
Volume = length * width * height
100 = 5 * W * 2.5
W = 100/ ( 5 * 2.5)
W = 8
Ethan is 1.85 meters tall. At 10 a.m., he measures the length of a tree's shadow to be 28.45 meters. He stands 24.3 meters away from the tree, so that the tip of his shadow meets the tip of the tree's shadow. Find the height of the tree to the nearest hundredth of a meter.

Answers
Answer:
12.68 mStep-by-step explanation:
Use the similarity of two triangles.
The ratio of corresponding sides is equal.
Let the height of the tree is x, then we have:
x / 1.85 = 28.45 / (28.45 - 24.3)x / 1.85 = 28.45 / 4.15x = 1.85*28.45 / 4.15x = 12.68 m (rounded)Answer:
12.68 m (nearest hundredth)
Step-by-step explanation:
Similar Triangle Theorem
If two triangles are similar, the ratio of their corresponding sides is equal.
Smaller triangle
height = Ethan's height = 1.85 mbase = 28.45 m - 24.3 m = 4.15 mLarger triangle
height = height of tree = h mbase = 28.45 mRatio of height to base:
\(\implies \sf height_{small}:base_{small}=height_{large}:base_{large}\)
\(\implies \sf 1.85:4.15=h:28.45\)
\(\implies \sf \dfrac{1.85}{4.15}=\dfrac{h}{28.45}\)
\(\implies \sf h= \dfrac{1.85}{4.15} \cdot 28.45\)
\(\implies \sf h=12.68\:m \:\:(nearest\:hundredth)\)
Therefore, the height of the tree to the nearest hundredth of a meter is 12.68 m.
Over an 80-day period, the number of leatherback sea turtle eggs on the two beaches can be modeled by A(x)=-0.25x^2+20x and B(x)=-0.19x^2+15.2x where x is the number of days.
Find (A+B)(x) and (A-B)(x)
Evaluate each expression when x=5
What is the meaning of (A-B)(x)?
Find the vertices and the intercepts of both.
Find where both are increasing and decreasing.
Answers
The sum (A+B)(x) and difference (A-B)(x) of two quadratic functions A(x) and B(x) were found, along with their values for x=5, vertices, intercepts, and where they are increasing/decreasing.
To find (A+B)(x), we simply add the two functions:
(A+B)(x) = A(x) + B(x) = (\(-0.25x^2+20x\)) + (\(-0.19x^2+15.2x\)) = \(-0.44x^2\) + 35.2x
To find (A-B)(x), we simply subtract B(x) from A(x):
(A-B)(x) = A(x) - B(x) = (\(-0.25x^2+20x\)) - (\(-0.19x^2+15.2x\)) = \(-0.06x^2\) + 4.8x
When x=5, we can evaluate each expression:
(A+B)(5) = \(-0.44(5)^2\) + 35.2(5) = 60
(A-B)(5) = \(-0.06(5)^2\) + 4.8(5) = 12
To find the vertices and intercepts of the functions A(x) and B(x), we can use the vertex and intercept formulas for quadratic functions:
For A(x):
Vertex = (-b/2a, f(-b/2a)) = (-20/-0.5, A(20/-0.5)) = (40, 400)
x-intercepts: 0 = \(-0.25x^2\) + 20x, so x = 0 or x = 80
y-intercept: A(0) = 0
For B(x):
Vertex = (-b/2a, f(-b/2a)) = (-15.2/-0.38, B(15.2/-0.38)) = (40, 304)
x-intercepts: 0 = \(-0.19x^2\) + 15.2x, so x = 0 or x = 80
y-intercept: B(0) = 0
Both functions are decreasing for x < 40, and increasing for x > 40. The vertex (40, 400) is the maximum point for A(x), and the vertex (40, 304) is the maximum point for B(x).
To learn more about quadratic functions please click on below link
https://brainly.com/question/29775037
#SPJ1
graph the parabola x=1/2(y-2)^2-4. find and graph the vertex, focus, directrix, and focal chord endpoints.
Answers
1. Find the graph of the parabola attached below
2. Vertex (-4, 2) Focus (-7/2, 2) Directrix (x = -9/2) Endpoints (-7/2, 1) (-7/2, 3)
How do we find the vertex, focus, directrix, and focal chord endpoints or the parabola?For the parabola, x = 1/2(y-2)² - 4 we will use the equation x = 4p(y-k)² + h,
Vertex → (h, k)
In our given equation, (y - 2) → (y - k), so k = 2. The term on the rightmost side of our equation (-4) → h in the form, so we know h = -4. ∴ vertex (-4, 2).
focus → (h, k) = (-4, 2); P = 1/2
Parabola is symmetric around the x axis and so the focus lies a distance P, from the center, along the x axis.
∴ Focus is (-4 + p, 2)
(-4 + 1/2, 2) ⇒ (-7/2, 2)
directrix → x = d
Parabola is symmetric around the x axis and therefore the directrix is a line paralled to the y axis a distance away from the ceter (-4, 2) x coordinate.
∴ x = -4 - p ⇒ x = -4 - 1/2
x = 9/2
focal chord endpoints →
The focus of the parabola is (-7/2, 2).
The y-coordinate of the focus is 2, so the y-coordinates of the endpoints of the focal chord are 2 + 1 and 2 - 1, → 3 and 1.
Therefore, the endpoints of the focal chord are:
(-7/2, 3) and (-7/2, 1).
Find more exercises on parabola;
https://brainly.com/question/11911877
#SPJ1

How many times does 41 go into 2583
Answers
Answer:
2583 i think
Step-by-step explanation:
what is 8x+6 simplified?
Answers
Answer:
4x+3
Step-by-step explanation:
8 and 6 are multiple of 2 so divide 8 /2 = 4 and divide 6/2=3
In the similar triangles below , what is the measure of D

Answers
In the given similar triangles below, we have to find the measure of Dwrite. Triangle 1, ABC, is similar to Triangle 2, DEF. The two triangles are similar because their corresponding angles are congruent and their sides are proportional.
In order to find the measure of Dwrite, we can use the concept of proportionality. The sides of similar triangles are proportional to each other.
This means that if we know the ratio of the sides of one triangle, we can use that ratio to find the corresponding sides of the other triangle. We can use this property to find the value of Dwrite.
To start, let's write down the ratio of the sides of Triangle 1 and Triangle 2. We can choose any two corresponding sides to do this, but we'll choose AB and DE because they are easiest to measure: AB/DE = 6/8.5We know that the measure of AB is 6, so we can solve for the measure of DE: DE = AB x (DE/AB)DE = 6 x (8.5/6)DE = 8.5Now we know that the measure of DE is 8.5.
We can use this to find the measure of Dwrite. We know that DE and Dwrite are corresponding sides of Triangle 2 and Triangle 1, respectively.
So we can write a proportion using the ratio of DE to Dwrite: DE/Dwrite = 8.5/xWe know that DE is 8.5, so we can substitute that in:8.5/Dwrite = 8.5/Now we can solve for x by cross-multiplying:8.5x = 8.5Dwrite = 1Therefore, the measure of Dwrite is 1.
For more such questions on triangles below
https://brainly.com/question/30146408
#SPJ8
At the school talent show, 1/3 of the people were boys, 3/6 were girls, and the rest were adults. If there were 50 more girls than adults, how many people were there in total? *
Answers
Answer:
150 people
Step-by-step explanation:
Lets call the total amount of people at the talent show x. Since 3/6=1/2, we know that half the people are girls, 1/3 are boys. If we added 1/2 and 1/3 we get 5/6, 1-5/6=1/6, so now we know that 1/6 of the people are adults. Because it says "If there were 50 more girls than adults" so from that we can see that 1/2x =1/6x+50. If we were to simplify the equation, we 1/3x=50, so x=150
Find g in the right triangle.

Answers
Answer:
34 degrees
Step-by-step explanation:
Before solving for g, we must remember that the inside of a triangle will always equal 180 degrees. Also, keep in mind that the little square at the top left corner of the triangle represents 90 degrees, so we can add both the existing degrees we know of:
90 + 56 = 146
And to find g, we simply subtract 180 by 146:
180 - 146 = 34
So, g is 34 degrees
Hope this helps :)
A six-sided die with sides labeled 1 through 6 will be rolled once. Each number is equally likely to be rolled. What is the probability of rolling a number greater than 2
Answers
Answer:
4/6 or 2/3. Depends if your teacher wants it reduced.
Step-by-step explanation:
Each number has a 1 out of 6 chance to be rolled. so it's 1/6 for rolling a 3, 1/6 for rolling a 4, 1/6 for rolling a 5, and 1/6 for rolling a 6. 4 x 1/6 = 4/6
Making the slope safer for skiers
Answers
Answer:
can u please put the whole question here.
Step-by-step explanation: