The co-interior angle of 105 degree is
Answers
Answer:
\(75 \: \: degrees\)
Step-by-step explanation:
\(180 - 105 =7 5\)
The sum of the co interior angles is 180 degrees
Related Questions
I deathly need help!

Answers
Answer:
So we rearrange the equation to R=I/PT
Then we substitute: R= 90/300(2)
Calculating the answer should be about 0.15
or I =15%
Step-by-step explanation:
To find the interest rate the formula give is
I = P x R x T.
Now substitute the variables.
90 = 300 x R x 2
90 = 600 x R
To find R we divide.
90/600 = .15
Now we substitute,
300 x .15 x 2 = 90
R = .15 or 15%
Hope this helps!
A square garden has an area of 400 square feet. Each side of the garden is (x-10) feet in length.
Write an equation that represents the AREA of the garden
Find the value of x using the square root method
What is the length of the side of the garden?

Answers
Answer:
400 = (x - 10)²
x² -20x -300 = 0
x = 30 and x = -10
Length side of the garden = 20 feet
Step-by-step explanation:
Given:
Area of square garden = 400 square feet
Length side of the garden = (x - 10) feet
Find:
Length side of the garden
Computation:
Area of square = side²
Area of square garden = Length side of the garden²
400 = (x - 10)²
400 = x² -20x + 100
x² -20x -300 = 0
x² -30x + 10x -300 = 0
x(x - 30) + 10(x - 30) = 0
(x - 30)(x + 10) = 0
So,
x = 30 and x = -10
Use x = 30 positive number
Length side of the garden = (x - 10) feet
Length side of the garden = (30 - 10) feet
Length side of the garden = 20 feet
A train is late arriving into a station.
It should arrive at 5 pm
It arrives at 5.15 pm.

Answers
Step-by-step explanation:
...
...
...............
.......
.
.
....
.
.

hi, can you please help me?
solve for EF
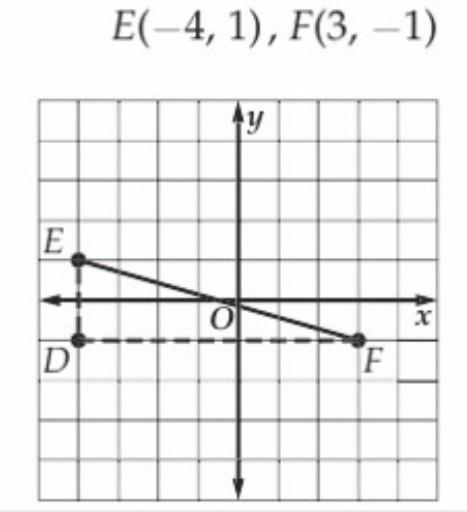
Answers
Answer:
I wish you and your family a very happy makar Sankranti ! May you are filled with extreme joy and happiness start a new year with great enthusiasm and positivity. ♥️
Answer:
see below
Step-by-step explanation:
ED = 2 units
DF = 7 units
EF^2 = 2^2 + 7^2
EF^2 = 4 + 49
EF^2 = 53
EF = 7.28
What are the respective names of the points of concurrency?.
Answers
The respective names of the point of concurrency is:
1. Circumcenter
2. Incenter.
3. Centroid
4. Orthocenter
Point of concurrency:
The point of concurrency is a point where three or more lines or rays intersect with each other.
Circumcenter:
The circumcenter is the point of concurrency of the perpendicular bisectors of all the sides of a triangle.
Incenter:
The incenter is the point of concurrency of the angle bisectors of all the interior angles of the triangle.
Centroid:
The point where three medians of the triangle meet is known as the centroid.
Orthocenter:
The point where three altitudes of the triangle meet is known as the orthocenter.
Learn more about the point of concurrency here:
https://brainly.com/question/7165324
#SPJ4

a bus arrives at 2:30 p.m. in Sydney if it left port if it left port Macquarie at 6.15 a.m the trip took
Answers
Answer:
Step-by-step explanation
Left at 6:15 am
How many hours until 2:15pm? 8 hours
How many minutes from 2:15 until 2:30? 15
So it took 8 hours and 15 minutes
Please answer the question on the attachment <3

Answers
Answer:
x = 5.8 ( rounded to nearest tenth)

Answer:
5.8 foot
Step-by-step explanation:
With reference angle 71
perpendicular (p)= x
base(b) = 2
Now
tan 71 = p/b
2.9 = x / 2
x = 5.8 foot
identify an intercept

Answers
Answer:
Step-by-step explanation:
An x- intercept would be -6 and a y-intercept would be -6 also.
Using the chart in your text, calculate how many hours per week you should ideally spend studying if you have one three-credit class that is less demanding, two three-credit classes that are typically demanding, and one four- credit class that is very challenging.
Answers
Using the same guideline, for a four-credit class, you would ideally spend:
4 credits * 2-3 hours/credit = 8-12 hours per week.
it is suggested that students allocate around 2-3 hours of study time per credit hour per week for a college-level course. However, the actual study time required may vary based on individual learning styles, prior knowledge, and the specific requirements set by professors or institutions.
Let's apply this general guideline to your scenario:
One three-credit class that is less demanding:
Assuming 2-3 hours of study per credit hour, for a three-credit class, you would ideally spend:
3 credits * 2-3 hours/credit = 6-9 hours per week.
Two three-credit classes that are typically demanding:
Similarly, for each of the two three-credit classes, you would spend:
3 credits * 2-3 hours/credit = 6-9 hours per week.
Since you have two such classes, the total time would be:
2 * (6-9) hours = 12-18 hours per week.
One four-credit class that is very challenging:
Using the same guideline, for a four-credit class, you would ideally spend:
4 credits * 2-3 hours/credit = 8-12 hours per week.
Learn more about credit from
https://brainly.com/question/30682995
#SPJ11
Question 5
Given the sequence, 35, 32, 29, 26, 23, ...
Find the following:
a1 =
Answers
Answer:
a1 = 2
Step-by-step explanation:
what does a1 mean?
35, 32 29, 26, 23, 20 , 17, 14, 11, 8, 5, (2)
A pebble falls off of a cliff at a height of
784 ft. If the equation for height as a
function of time is
h(t) = -16t2 + initial height where t is time
in seconds and h(t) is height in feet, how
many seconds will it take for the pebble
to hit the ground?
Answers
Answer:
7 seconds
Step-by-step explanation:
You would get 49 from doing -784 divided by -16 then you do the square root of 49 which is 7
ANSWER= 7 seconds
The time taken by the pebble to hit the ground will be = 7 seconds
What is an Algebraic Equation?Expression we get when operations such as addition , subtraction , multiplication , division , are operated upon on variable and constants.
Equation of height as a function of time = h(t) = - 16 (t^2)
cliff is at a height of = 784 feet
comparing both the above equation , we get
-16 (t^2) = 784
t^2 = 49
t = 7 seconds
The time taken by the pebble to hit the ground will be = 7 seconds
Learn more about Algebraic Equation:
https://brainly.com/question/953809?referrer=searchResults
#SPJ2
A bus arrives every 10 minutes at a bus stop. It is assumed that the waiting time for a particular individual is a random variable with a continuous uniform distribution.
a) What is the probability that the individual waits more than 7 minutes?
b) What is the probability that the individual waits between 2 and 7 minutes?A continuous random variable X distributed uniformly over the interval (a,b) has the following probability density function (PDF):fX(x)=1/0.The cumulative distribution function (CDF) of X is given by:FX(x)=P(X≤x)=00.
Answers
In the following question, among the various parts to solve- a) the probability that the individual waits more than 7 minutes is 0.3. b)the probability that the individual waits between 2 and 7 minutes is 0.5.
a) The probability that an individual will wait more than 7 minutes can be found as follows:
Given that the waiting time of an individual is a continuous uniform distribution and that a bus arrives at the bus stop every 10 minutes.Since the waiting time is a continuous uniform distribution, the probability density function (PDF) can be given as:fX(x) = 1/(b-a)where a = 0 and b = 10.
Hence the PDF of the waiting time can be given as:fX(x) = 1/10The probability that an individual waits more than 7 minutes can be obtained using the complementary probability. This is given by:P(X > 7) = 1 - P(X ≤ 7)The probability that X ≤ 7 can be obtained using the cumulative distribution function (CDF), which is given as:FX(x) = P(X ≤ x) = ∫fX(t) dtwhere x ∈ [a,b].In this case, the CDF of the waiting time is given as:FX(x) = ∫0x fX(t) dt= ∫07 1/10 dt + ∫710 1/10 dt= [t/10]7 + [t/10]10= 7/10Using this, the probability that an individual waits more than 7 minutes is:P(X > 7) = 1 - P(X ≤ 7)= 1 - 7/10= 3/10= 0.3So, the probability that the individual waits more than 7 minutes is 0.3.
b) The probability that the individual waits between 2 and 7 minutes can be calculated as follows:P(2 < X < 7) = P(X < 7) - P(X < 2)Since the waiting time is a continuous uniform distribution, the PDF can be given as:fX(x) = 1/10Using the CDF of X, we can obtain:P(X < 7) = FX(7) = (7 - 0)/10 = 0.7P(X < 2) = FX(2) = (2 - 0)/10 = 0.2Therefore, P(2 < X < 7) = 0.7 - 0.2 = 0.5So, the probability that the individual waits between 2 and 7 minutes is 0.5.
For more such questions on probability
https://brainly.com/question/24756209
#SPJ11
use induction to prove that pn i=1(2i − 1)3 = n 2 (2n 2 − 1) whenever n is a positive integer.
Answers
The statement is proven true by induction: for any positive integer n, the sum of (2i - 1)³ from i = 1 to n is equal to n²(2n² - 1).
To prove the statement using mathematical induction, we need to establish two conditions: the base case and the inductive step.
Base Case:
Let's start with the base case, where n = 1.
When n = 1, we have p₁ ∑ (2i - 1)³ = 1³ = 1.
On the right-hand side, we have 1 * (2 * 1² - 1) = 1.
Since the statement holds true for n = 1, the base case is satisfied.
Inductive Step:
Next, we assume that the statement holds true for some positive integer k, i.e., pₖ ∑ (2i - 1)³ = k²(2k² - 1).
Now, we need to prove that the statement also holds for n = k + 1, i.e., pₖ₊₁ ∑ (2i - 1)³ = (k + 1)²(2(k + 1)² - 1).
Starting with the left-hand side:
pₖ₊₁ ∑ (2i - 1)³ = (pₖ ∑ (2i - 1)³) + (2(k + 1) - 1)³
= k²(2k² - 1) + (2k + 1)³ (using the inductive hypothesis)
= 2k⁴ - k² + 8k³ + 12k² + 6k + 1
Simplifying the right-hand side:
(k + 1)²(2(k + 1)² - 1) = (k² + 2k + 1)(2k² + 4k + 2 - 1)
= 2k⁴ + 4k³ + 2k² + 4k³ + 8k² + 4k + 2k² + 4k + 2 - k² - 2k - 1
= 2k⁴ + 8k³ + 12k² + 6k + 1
Comparing the left-hand side and right-hand side, we can see that they are equal.
Therefore, by the principle of mathematical induction, the statement is proven true for all positive integers n.
To know more about mathematical induction refer here:
https://brainly.com/question/1333684#
#SPJ11
hello please help i’ll give brainliest

Answers
Answer:
Step-by-step explanation:
The answer I believe is $5.44
if ribbon candy costs 2.50 per foot. How many feet can you buy if u have 11.25
Answers
Assume that you are aboard a research submarine doing submerged training exercises in the Pacific Ocean. At time t = 0, you start porpoising (going alternately deeper and shallower). At time t = 4 min you are at your deepest, y = -1000 m. At time t = 9 min you next reach your shallowest, y = -200 m. Assume that y varies sinusoidally with time.
Write an equation expressing y as a function of t.
Answers
The equation expressing y as a function of t is y(t) = A * sin(B(t - C)) + D, where A is the amplitude, B is the frequency, C is the phase shift, and D is the vertical shift.
To express y as a function of t, we can use a sinusoidal function due to the given information that y varies sinusoidally with time. The general form of a sinusoidal function is y(t) = A * sin(B(t - C)) + D, where A represents the amplitude, B represents the frequency, C represents the phase shift, and D represents the vertical shift.
In this scenario, we are provided with the deepest point at t = 4 min, where y = -1000 m, and the shallowest point at t = 9 min, where y = -200 m. These points allow us to determine the amplitude and vertical shift of the sinusoidal function. The amplitude is the absolute value of half the difference between the deepest and shallowest points, which in this case is |(-1000 - (-200))/2| = 400 m. The vertical shift is the average of the deepest and shallowest points, which is (-1000 + (-200))/2 = -600 m.
The frequency and phase shift are not explicitly given in the problem statement. Without this information, it is not possible to determine the specific values of B and C. Therefore, the equation expressing y as a function of t becomes y(t) = A * sin(B(t - C)) + D, where A = 400 and D = -600. The variables B and C would depend on the specific characteristics of the porpoising motion, which are not provided in the problem.
Learn more about Frequency : brainly.com/question/27884844
#SPJ11
Solve the system of equations by substitution:3y - 6x = 248 + 2x = yA.infinite solutionsB.(2,12)C.no solutionD.(0,8)
Answers
Given the equations:
3y - 6x = 24..............................1
8 + 2x = y..................................2
Substitute (8 + 2x) for y in equation 1.
3(8 + 2x) - 6x = 24
24 + 6x - 6x = 24
24 = 24
Since, we have 24 = 24, we can say the system of equations have infinite solutions.
ANSWER:
A. infinite solutions
A three sided regular polygon is called _______.
an acute triangle
a right triangle
an isosceles triangle
an equilateral triangle
Answers
Answer:
Equilateral triangle
Step-by-step explanation:
Mike knows that (3,6.5) and (4,17.55) are points on the graph of an exponential function, g(x), and
he wants to find another point on the graph of this function.
First, he subtracts 6.5 from 17.55 to get 11.05.
Next, he adds 11.05 and 17.55 to get 28.6.
He states that (5,28.6) is a point on g(x).
Is he correct? Explain your reasoning.
Answers
Mike's claim that (5,28.6) is a point on the exponential function g(x) is incorrect
How to determine if he is correct?The points are given as:
(3,6.5) and (4,17.55)
Calculate the rate of change using:
r = y4/y3
This means that:
r = 17.55/6.5
r = 2.7
So, the next point on the graph is:
Next point = 2.7 * y4
Substitute 17.55 for y4
Next point = 2.7 * 17.55
Evaluate
Next point = 47.39
This means that the next point on the graph is (5,47.99)
Hence, Mike's claim that (5,28.6) is a point on the exponential function g(x) is incorrect
Read more about exponential graphs at:
https://brainly.com/question/27859284
#SPJ1
Issac surveyed the employees at the law firm each employee was asked to record their highest level of education completed. Two hundred sixty six woolens completed the survey . How many of those people completed graduate school?
Answers
Complete Question :
Isaac surveyed the employees at a law firm. Each employee was asked to record their highest level of education completed. The
results are shown in the table below.
Highest Level of Education Completed
Education Level
Percentage
High School
5%
Community College
10%
Four-Year College
60%
Graduate School
25%
Two-hundred sixty people completed the survey. How many of those people completed graduate school?
Answer:
65 people
Step-by-step explanation:
Given the following :
Number of survey participants = 260
Percentage that completed graduate school = 25%
Number of participants who completed graduate school ;
Total Number of participants × percentage that completed graduate school
260 participants × 25%
260 × 0.25
= 65
Answer:
65 people
Step-by-step explanation:
I took the test and that was the correct answer
Help me solve this problem

Answers
Answer:
Step-by-step explanation:
3x - 7x -21 < -13
-4x < -13 + 21
-4x < 8
x > -2
\(3x - 7(x + 3) < -13 \\3x - 7x - 21 < -13 \\3x - 7x < -13 + 21 \\-4x < 8 \\x > -2\)
Find an equivalent system of equations for the following system: (1 point) 2x + 4y = 4 −5x + 5y = 5
Answers
Answer: To find an equivalent system of equations, we can use algebraic operations to manipulate the original equations while preserving the solutions.
One way to eliminate one of the variables is to multiply one of the equations by a constant that will make the coefficients of one of the variables in the two equations opposite in sign. Here, we can multiply the first equation by -5 and the second equation by 2 to eliminate the x variable:
-10x - 20y = -20
10x - 10y = 10
Adding these two equations, we get:
-30y = -10
Dividing both sides by -30, we get:
y = 1/3
Substituting this value of y into one of the original equations, we can solve for x:
2x + 4(1/3) = 4
2x + 4/3 = 4
2x = 8/3
x = 4/3
Therefore, an equivalent system of equations is:
x = 4/3
y = 1/3
These two equations have the same solution as the original system.
Step-by-step explanation:
will give brainliest and 50 points if u get this right

Answers
The slope of this line is m = 1.
An equation of this line is y = x.
How to calculate the slope of a line?In Mathematics, the slope of any straight line can be determined by using this mathematical equation;
Slope (m) = (y₂ - y₁)/(x₂ - x₁)
Based on the information provided, we can logically deduce the following data points on the line:
Points on x-axis = (0, 1).Points on y-axis = (0, 1).Substituting the given data points into the slope formula, we have the following;
Slope (m) = (y₂ - y₁)/(x₂ - x₁)
Slope (m) = (1 - 0)/(1 - 0)
Slope (m) = 1/1
Slope (m) = 1
At data point (1, 1), an equation of this line can be calculated by using the point-slope form as follows:
y - y₁ = m(x - x₁)
Where:
m represents the slope.x and y represents the data points.y - 1 = 1(x - 1)
y = x - 1 + 1
y = x
Read more on slope here: brainly.com/question/3493733
#SPJ1

5. When the probability of event B is affected by he occurrence of event A, the events are not independent. Let P(B | A) denote the probability of B given the condition that A has occurred. This is called a conditional probability.
Type I by holding down shift and type \
For independent events A and B, P(B | A) = P(b), and P(A | B)= P(A)
For dependent events A and B
P(B | A) not equal P(B). The occurrence of A has changed the probability of B.
P(A | B) not equal P(A). The occurrence of B has changed the probability of A.
For dependent events, P(A and B) = P(A) x P(B | A) = P(B) x P(A | B). This is the General Multiplication Rule.
Assume the following joint and marginal probabilities:
In favor Democrat Republican row total
Yes 0.15 0.20 0.35
No 0.25 0.40 0.65
Column
When we know the condition that some event has occurred, the table reduces to a row or column matching the condition. For example, when we know that the party is democrat, the table reduces to the democrat column:
In Favor Democrat
Yes 0.15
No 0.25
Column total 0.40
P(Yes | Democrat) is the probability of event Yes given the condition that the event Democrat has occurred. In condition Democrat, yes occurs at a rate of 0.15 and 0.40. So P(Yes | Democrat) = 0.15/0.40 = 0.375.
P(male | republican) is a ___________ probability
Marginal
Conditional
joint
Answers
P(male | republican) is a conditional probability.
A conditional probability is a type of probability that measures the likelihood of an event occurring given that another event has already occurred.
The given information is :
Gender Republican Total
Male 0.35 0.70
Female 0.25 0.50
Total 0.60 1.20
To calculate P(male | republican), we can use the formula for conditional probability:
P(male | republican) = P(male and republican) / P(republican)
we have P(republican) = 0.60 (the proportion of people who are Republican) and
P(male and republican) = 0.35 (the proportion of people who are both male and Republican).
Plugging these values into the formula, we get:
P(male | republican) = 0.35 / 0.60
= 0.5833
Hence, P(male | republican) is a conditional probability.
To learn more on probability click:
https://brainly.com/question/11234923
#SPJ12
Write down the inequality described by "half of x is no more than six", and solve it
Answers
(the > has a line under it but idk how to type that lol)
X and rounds it down to the nearest integer. Find INT (x) for x=-4.6, 2.3, and 2 then find the domain and range
Answers
The range of rounds down nearest integer function is {-2,1,5} while domain is {-2.3,√2,4.6}.
What is the range and domain of a function?A function's range is the set of all values that the function accepts, and its domain is the set of all values for which the function is defined.
Given the rounds down nearest integer function INT(x)
x = -2.3,√2,4.6
Since the domain is the set of all x's values thus {-2.3,√2,4.6} will be the domain.
For x = -2.3 ⇒ INT(-2.3) = -2
For x = √2 = 1.414 ⇒ INT(√2) = 1
For x = 4.6 ⇒ INT(4.6) = 5
So range {-2,1,5}
Hence "The range of rounds down nearest integer function is {-2,1,5} while domain is {-2.3,√2,4.6}".
For more details about the range and domain of the function,
brainly.com/question/28135761
#SPJ1
What is the equation of the line that passes through the point (−6,4) and has a slope of negative 5 over 6
Answers
Answer:
y = -5/6x -1
Step-by-step explanation:
The three components needed to create the equation of a line are: the x and y coordinates, the slope, and the y intercept.
Both the x and y coordinates and the slope is given. To find the y intercept, we will create an equation following the template of point-slope form.
y = slope * x + y int.
4 = -5/6 * -6/ + y int.
4 = 5 + y int.
y int. = -1
We will reinstate this into our equation, and this will be our answer!
y = -5/6x -1
This is the equation!
What is the constant of proportionality, \dfrac{y}{x}xystart fraction, y, divided by, x, end fraction ?
Answers
The constant of proportionality in the expression \(\frac{y}{x}xy\) is \(xy\).
The given expression \(\frac{y}{x}xy\) can be simplified as \(\frac{y}{x} \cdot xy\).
To find the constant of proportionality, we look at the coefficient that multiplies both \(x\) and \(y\), which in this case is \(xy\). This means that for every \(x\) unit increase, there will be a \(y\) unit increase, and the ratio between \(y\) and \(x\) is constant and equal to \(xy\).
Therefore, the constant of proportionality in the expression \(\frac{y}{x}xy\) is \(xy\), which represents the relationship between \(y\) and \(x\) in the given expression.
To learn more about constant of proportionality; -brainly.com/question/17793140
#SPJ11
A car travels at 1/2t^2+55 mph for 0≤x≤5 hours. Approximately how far does it travel?
Answers
PLEASE HELPPPPPPPPPPP MEEEEEEE

Answers
The following are the measures of angles and sides using the sine and cosine rules:
1). QR = 15, m∠P = 52°, m∠Q = 43°
2). BC = 21, DC = 10.4, m∠C = 22°
3). VX = 10.7, WX = 10.2, m∠V = 39°
4). HF = 18.4, m∠H = 28.7, m∠F = 15.3
What is the sine and cosine rulesThe sine rule is a relationship between the size of an angle in a triangle and the opposing side. While the cosine rule relates the lengths of the sides of a triangle to the cosine of one of its angles.
1). Using the sine rule:
19/sin85 = 13/sunQ
Q = sin⁻¹[(13 × sin85)/19] {cross multiplication}
Q = 43
m∠P = 180° - (85 + 43) = 52°
QR = sin⁻¹[(19 × sin52)/sin85]
QR = 15.
2). m∠C = 180 + (19 + 139) = 22°
Using the sine rule:
BC = (12 × sin139)/sin22
BC = 21.
DC = (12 × sin19)/sin22
DC = 10.4
3). m∠V = 180 - (41 + 100) = 39°
Using the sine rule:
VX = (16 × sin41)/sin100
VX = 10.7
WX = (16 × sin39)/sin100
WX = 10.2
4). Using the cosine rule:
HF² = 7² + 13² - 2(7)(13)cos136°
HF = √338.8491
HF = 18.4
applying sine rule;
F = sin⁻¹[(7 × sin136)/18.4]
F = 15.3
m∠H = 180 - (15.3 + 136) = 28.7
Therefore, the measures of angles and sides using the sine and cosine rules are:
1). QR = 15, m∠P = 52°, m∠Q = 43°
2). BC = 21, DC = 10.4, m∠C = 22°
3). VX = 10.7, WX = 10.2, m∠V = 39°
4). HF = 18.4, m∠H = 28.7, m∠F = 15.3
Read more about sine cosine rule here:https://brainly.com/question/4372174
#SPJ1