the capacity of a cylinder varies jointly with its height and the square of its radius. if a cylinder with a radius of 3 3 centimeters and a height of 6 6 centimeters has a capacity of 169.56 169.56 cubic centimeters, what will the capacity be of a cylinder with radius 2 2 centimeters and height 7 7 centimeters?
Answers
The capacity of the cylinder with a radius of 2 cm and height of 7 cm is approximately 26.208 cubic centimeters.
The formula for the capacity of a cylinder is:
C = πr^2h
where C is the capacity, r is the radius, and h is the height.
We are told that the capacity varies jointly with the height and the square of the radius, which means that we can write:
C = k r^2 h
where k is the constant of proportionality.
To find k, we can use the given information about the cylinder with a radius of 3.3 cm and height of 6.6 cm:
\(169.56 = k (3.3)^2 (6.6)\)
Simplifying, we get:
k ≈ 0.936
Now we can use this value of k to find the capacity of the cylinder with a radius of 2 cm and height of 7 cm:
\(C = k (2)^2 (7)\)
C ≈ 26.208 cubic centimeters
Therefore, the capacity of the cylinder with a radius of 2 cm and height of 7 cm is approximately 26.208 cubic centimeters.
Learn more about the capacity of the cylinder at
brainly.com/question/28810247
#SPJ4
Related Questions
Please help it about calculus

Answers
The total distance travelled by the particle is 24 units.
What is displacement?
Displacement is defined as a change in an object's position. An object's displacement is defined as how far it has moved from its starting point. The dependent variable in the displacement time graph is displacement, which is represented on the y-axis, and the independent variable is time, which is represented on the x-axis. Position-time graphs are another name for displacement time graphs.
The displacement curve is given for 0 ≤ t ≤ 18.
We need to find the total distance of the curve, it will be the positive sum of all displacements.
So, total distance = (7-0) + (3-0) + (2+3) + (2+4) + (7-4)
= 7 + 3 + 5 + 6 + 3
= 24
Hence, the total distance is 24 units.
To learn more about displacement
https://brainly.com/question/12329052
#SPJ1
I’m not sure this is right can someone please revise me

Answers
In the past, the output of a process had a mean of 2.050 and a standard deviation of 0.020 liters. order")?
Answers
First, let's calculate the z-score for the value 2.025 liters using the formula:
z = (x - μ) / σ
Where:
x = the value we want to calculate the probability for (2.025 liters)
μ = the mean of the process (2.050 liters)
σ = the standard deviation of the process (0.020 liters)
Plugging in the values:
z = (2.025 - 2.050) / 0.020
Simplifying:
z= -0.025 / 0.020
z = -1.25
Now, we can look up the probability corresponding to a z-score of -1.25 in the standard normal distribution table or use a calculator.
Using a standard normal distribution table, the probability is approximately 0.1056. This means that the probability of randomly selecting an output from the process that is less than 2.025 liters is approximately 0.1056 or 10.56%.
Alternatively, you can use a calculator or statistical software to find the probability directly by looking up the cumulative distribution function (CDF) of the standard normal distribution at -1.25. The result will also be approximately 0.1056 or 10.56%.
Learn more about Cumulative Distribution Function here:
https://brainly.com/question/30402457
#SPJ11
indentify the range, y=2x + 6
Answers
x
can take any value, the Domain of this equation is the set of all Real Numbers:
{
R
}
Because this is a simple linear transformation, the Range of this equation is also the set of all Real Numbers:
{
R
}
27. Table 2 show rates of tax on salary per month for certain country. Table 2. Salary per month Tax rate First K9000.00 % (tax free) Next K10000.00 15% Next K12000.00 25% Next K15000.00 35% If a worker earns K30000.00 per month, calculate the worker's monthly tax. 25%
Answers
The amount of the worker monthly tax will equals to K4,850.
What are worker income tax?An income tax refers to the tax imposed on individuals or entities in respect of the income earned by them. It is computed as the product of a tax rate times the taxable income. They may vary by type or characteristics of the taxpayer and the type of income
To calculate the worker's monthly tax, we need to determine the amount of salary that falls into each tax bracket and then calculate the tax owed for each bracket:
For a monthly salary of K30,000, the first K9,000 is tax-free, leaving K21,000 to be taxed. Of this K21,000, the first K10,000 is taxed at 15%, which gives a tax of K1,500. The next K12,000 is taxed at 25%, which gives a tax of K3,000.Finally, the remaining K-1,000 is taxed at 35%, which gives a tax of K350.The worker's monthly tax is then computed as:
= K1,500 + K3,000 + K350
= K4,850.
Read more about monthly tax
brainly.com/question/30689717
#SPJ1
f the following, which is the smallest sample size that will result in a margin of error of no more than 5 percentage points? responses 73 73 97 97 271 271 385 385 1,537 1,537 skip to navigation
Answers
The smallest sample size that will result in a margin of error of no more than 5% for a 95% confidence interval is given as follows:
385.
What is a confidence interval of proportions?A confidence interval of proportions has the bounds given by the rule presented as follows:
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which the variables used to calculated these bounds are listed as follows:
\(\pi\) is the sample proportion, which is also the estimate of the parameter.z is the critical value.n is the sample size.The margin of error is modeled as follows:
\(M = z\sqrt{\frac{\pi(1-\pi)}{n}}\)
The confidence level is of 95%, hence the critical value z is the value of Z that has a p-value of \(\frac{1+0.95}{2} = 0.975\), so the critical value is z = 1.96.
We have no estimate, hence we consider that:
\(\pi = 0.5\)
The minimum sample size is obtained as n when M = 0.05, hence:
\(M = z\sqrt{\frac{\pi(1-\pi)}{n}}\)
\(0.05 = 1.96\sqrt{\frac{0.5(0.5)}{n}}\)
\(0.05\sqrt{n} = 1.96 \times 0.5\)
\(\sqrt{n} = 1.96 \times 10\) (0.5/0.05 = 10).
\((\sqrt{n})^2 = (1.96 \times 10)^2\)
n = 384.16
Hence rounded to 385, as a sample size of 384 would have a margin of error slightly above 0.05.
More can be learned about the z-distribution at https://brainly.com/question/25890103
#SPJ1
One number is 876.2 more than twice the other. If the sum of the two numbers is 2005.46, find the larger of the two numbers?
Answers
Answer:
these .56 because they are bigger
Step-by-step explanation:
hope this helps
is there a difference in salary for different racial groups? a study compares the average salary for blacks, whites and hispanics, based on random samples of 10 people in each racial group. the standard deviations of the groups were quite different.
Answers
There is a difference in the average salary among the three racial groups being studied.
A study was conducted comparing the average salary for Blacks, Whites, and Hispanics, using random samples of 10 people in each racial group. The standard deviations of the groups were quite different.
To determine if there is a significant difference in salaries among these racial groups, the following steps can be taken:
1. Calculate the mean salary for each racial group (Blacks, Whites, and Hispanics) using the data from the random samples.
2. Calculate the variance and standard deviation for each group's salary to understand the spread of data within each group.
3. Perform an analysis of variance (ANOVA) test, which helps in comparing the means of multiple groups (in this case, the three racial groups). This test will indicate whether there is a significant difference in the mean salaries of the groups.
If the results of the ANOVA test show a significant difference, it means there is a difference in the average salary among the three racial groups being studied.
Learn more about average here,
https://brainly.com/question/29509552
#SPJ11
Prove the following:
1 + cos^2 A = 2 ( cos^4A + sin^4A)
Answers
The 2 sides of the equation are not equal; hence, I cannot prove them to be true.
2.6 A printer can print 12 color pages in 3 minutes. How many color pages can the printer print in 9 minutes?
Answers
Answer:
36
Step-by-step explanation:
12 times 3 = 36
Can someone explain or help me with this?

Answers
Answer:
Step-by-step explanation:
6085 rounded to the nearest hundred is 6100
51,672 rounded to the nearest ten thousand is 50,000
What is the mean of the data set? 1, 1, 2, 1, 3, 2, 2, and 3
Answers
Answer:
the mean is 1.875
Step-by-step explanation:
1+1+1+2+2+2+3+3=15
15/8 = 1.875
mean Is sum of all numbers divided by total amount of numbers
Write down the inequality described by "negative three groups of x is less than two", and solve for x
Answers
Answer:
- 3x < 2
x < - 1
Explanation and Check part below
Explanation and Check part belowHope this helps :)
Step-by-step explanation:
1. To solve, first isolate the variable by doing the inverse operation which is in this case dividing by - 3 on both sides of the equation.
- 3x < 2
- 3 -3
x < - 1
2. Graph it if needed with an open dot because - 1 is not part of the set of solutions.
<--------○
<----l----l-----l----->
-2 -1 0
Check:
1. Substitute x with any number less than - 1 and solve.
- 3 (- 2) < 2
-6 < 2
True statement.
John is planning to drive to a city that is 450 miles away. If he drives at a rate of 50 miles per hour during the trip, how long will it take him to drive there?
Answer, ___ Hours. For 100 points
Answers
Answer: 9 hours
Step-by-step explanation: divide 450 total miles by how many miles you drive per hour (50).
I will brainliest if correct! The graph of an exponential model in the form y=aXb^x passes through the points (3,5) and (4,10). Which point is also on the graph?(Multiple choice)

Answers
Answer:
The fourth choice.
Step-by-step explanation:
An exponential function passes through (3, 5) and (4, 10).
And we want to determine which other point is also on the graph.
First, we can find the exponential function. A standard exponential function is in the form:
\(y=a(b)^x\)
The point (3, 5) tells us that y = 5 when x = 3. Thus:
\(5=a(b)^3\)
The point (4, 10) tells us that y = 10 when x = 4. Thus:
\(10=a(b)^4\)
In the first equation, we can divide both sides by a:
\(\displaystyle \frac{5}{a}=b^3\)
And we can rewrite the second equation:
\(\displaystyle 2(5)=a(b^4)\Rightarrow 2\Big(\frac{5}{a}\Big)=b^4\)
Substitute:
\(2b^3=b^4\)
Divide:
\(b=2\)
Using the first equation again, substitute:
\(5=a(2)^3\)
Simplify and solve:
\(5=a(8)\Rightarrow \displaystyle a=\frac{5}{8}\)
So, our exponential function is:
\(\displaystyle y=\frac{5}{8}(2)^x\)
Next, we can simply try each point and see which point is correct.
Testing the first point (remember that (2,0) means that y = 0 when x = 2):
\(\displaystyle 0\stackrel{?}{=}\frac{5}{8}(2)^0=\frac{5}{8}(1)=\frac{5}{8}\neq 0\)
Testing the second point:
\(\displaystyle 1\stackrel{?}{=}\frac{5}{8}(2)^2=\frac{5}{8}(4)=\frac{5}{2}\neq 1\)
The third point:
\(\displaystyle 15\stackrel{?}{=}\frac{5}{8}(2)^5=\frac{5}{8}(32)=5(4)=20\neq 15\)
And the fourth point:
\(\displaystyle 20\stackrel{?}{=}\frac{5}{8}(2)^5=\frac{5}{8}(32)=5(4)=20\stackrel{\checkmark}{=}20\)
Therefore, D is the correct choice.
Answer:
(2,0)
Step-by-step explanation:
The answer is (2,0) because the number line passes through that point

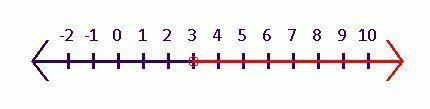
Graph the solution to this inequality on the number line.
0.3(x − 4) > -0.3
Answers
Answer:
Please refer to the attached image in the answer area.
Step-by-step explanation:
The given inequality is:
\(0.3(x -4) > -0.3\)
To find:
The graph of inequality on the number line.
Solution:
First of all, let us simplify the inequality.
\(0.3(x -4) > -0.3\)
Dividing it with 0.3 on the both sides:
\(x -4 > -1\\\text{Adding 4 on both sides}\\\Rightarrow x > 3\)
i.e. all the values x > 3 will be our solution. There is no equal sign in the inequality so 3 will not be included in the solution.
Please refer to the attached image for the solution graph of the given inequality.
3 has an empty circle drawn over it which signifies that 3 is not included in the solution set.
Red line shows that all the values greater than 3 are included in the solution.
You are ordering a hamburger and can get up to 6 toppings, but each topping can only be used once. You tell the cashier to surprise you with the toppings you get.What is the probability that you get 3 toppings? Express your answer as a fraction or a decimal number rounded to four decimal places.
Answers
Answer:
1/120
Explanation:
The number of possible toppings = 6
Each topping can only be used once.
We want to find the probability that you get 3 toppings.
\(\begin{gathered} \text{P\lparen1st topping\rparen}=\frac{1}{6} \\ \text{P\lparen2nd topping\rparen}=\frac{1}{5} \\ \text{ P\lparen3rd topping\rparen}=\frac{1}{4} \end{gathered}\)Therefore, the probability that you get 3 toppings is:
\(\begin{gathered} \text{ P\lparen3 toppings\rparen}=\frac{1}{6}\times\frac{1}{5}\times\frac{1}{4} \\ =\frac{1}{120} \end{gathered}\)The probability that you get 3 toppings is 1/120.
How do you evaluate the definite integral ∫2^x dx from [−1,1]?
Answers
The solution for definite integral ∫2^x dx from [−1,1] is
3/ 2 ln2
Definite Integral:
A definite integral is defined as the exact limit and summation examined in the previous section to find the net area between the function and the x axis. Also note that the definite integral notation is very similar to the indefinite integral notation. The reason for this will become clear in due course.
There are a few terms that should be left out along the way. The number "a" below the integral sign is called the lower integral limit, and the number "b" above the integral sign is called the upper integral limit. Even if the intervals a and b are specified, the lower bound is not necessarily less than the upper bound. Collectively, a and b are often referred to as the interval of integration.
Given a function :
f(x) that is continuous function on the interval [a , b]
we divide the interval into n subintervals of equal breadth, Δx, and from each interval choose a point, x i. Then the definite integral of f(x) from a to b is
\(\int\limits^b_a f(x) \, dx = \lim_{n \to \infty} f(xi)\) Δx.
According to the question:
let's start by differentiating 2ˣ.
y = 2ˣ
⇒ ln y = x ln 2
⇒ 1/y dy/dx = ln2
⇒ d /dx = y ln 2 = 2ˣ ln2
So remembering integration is the reverse of differentiating.
y = 2ˣ
⇒ dy/dx = 2ˣ ln 2
⇒ ∫2ˣ dx = 2ˣ / ln 2 + C
2ˣ > 0, ∀ x ∈ R, there is no negative area so we can
Insert the limits and evaluate immediately.
= 1/ ln2 [2x]\(\left \{ {{y= -1} \atop {x=1}} \right.\)
= 1/ln 2 (2¹ - 2⁻¹)
= 3/ 2ln 2
Learn more about Definite Integral:
https://brainly.com/question/29685762
#SPJ4
-12+(-5)
please show work
Answers
Answer:
-17
Step-by-step explanation:
-12 + (-5) is basically subtracting 5 from -12.
Or you can think of it as adding 5 to 12. Then make the answer negative.
Hope I helped :)
Please consider Brainliest :)
Answer all questions and show all of your work. 1. Consider Verizon data speeds (Mbps): 20, 50, 22, 14, 23, 10. Find the following values for these data. (a) Mean (b) Median (e) Sample Variance s² (d
Answers
The mean, median, and sample variance of the given dataset are:Mean = 23.17Median = 21Sample variance = 173.5592
(a) Mean The mean (or average) of a dataset is calculated by summing up all the values and dividing by the total number of values.
The formula for calculating the mean is: `mean = (sum of values) / (total number of values)`For the given dataset, we have:20, 50, 22, 14, 23, 10
Sum of values = 20 + 50 + 22 + 14 + 23 + 10 = 139
Total number of values = 6Therefore, the mean is given by: `mean = 139 / 6 = 23.17`Answer: 23.17 (rounded to two decimal places)
(b) Median To find the median, we need to arrange the dataset in increasing order:10, 14, 20, 22, 23, 50The median is the middle value of the dataset. If there are an odd number of values, the median is the middle value. If there are an even number of values, the median is the average of the two middle values. Here, we have 6 values, so the median is the average of the two middle values: `median = (20 + 22) / 2 = 21` Answer: 21(e)
Sample variance s²The sample variance is calculated by finding the mean of the squared differences between each value and the mean of the dataset.
The formula for calculating the sample variance is: `s² = ∑(x - mean)² / (n - 1)`where `∑` means "sum of", `x` is each individual value in the dataset, `mean` is the mean of the dataset, and `n` is the total number of values.For the given dataset, we have already calculated the mean to be 23.17.
Now, we need to calculate the squared differences between each value and the mean:
20 - 23.17 = -3.1722 - 23.17
= -1.170 - 23.17
= -13 - 23.17
= -9.1723 - 23.17
= -0.1710 - 23.17
= -13.17
The sum of the squared differences is given by:
∑(x - mean)² = (-3.17)² + (-1.17)² + (-13.17)² + (-9.17)² + (-0.17)² + (-13.17)²
= 867.7959
Therefore, the sample variance is given by: `s² = 867.7959 / (6 - 1) = 173.5592`Answer: 173.5592 (rounded to four decimal places)
The mean, median, and sample variance of the given dataset are:Mean = 23.17Median = 21Sample variance = 173.5592
To know more about sample variance visit:
brainly.com/question/30112124
#SPJ11
Can you help me solve this!

Answers
Hello!
surface area
= 2(6*2) + 2(4*2) + 4*6
= 2*12 + 2*8 + 24
= 24 + 16 + 24
= 64 square inches
PLEASE HELP ME ASAP RIGHT ANSWERS ONLY!
What is the slope of the line?

Answers
hi
Slope is 2 .
here is how you do the trick : by reading on the graph
if you go forward of 1 on the X axis , how much did the line goes up or down ?
Here at 0 on X- axis, we are at 0 on the Y- axis.
If you go forward of 1 on X axis, you are at 2 on Y axis.
So the slope is + 2
Other technique by calculus between two points.
Take two diffents point on the X axis. Call them A and B
Slope is : ( f(A) -f(B) ) / A-B
exemple here : we have two easy points . Take 0 as A and 1 as B
We read on the graph :
A = 0 and B = 1
f(A)= 0 and f(B) = 2
Now we apply formula :
( f(A) -f(B) ) / (A-B )
(0 -2 ) / (0-1) = -2/-1 = 2
Slope is 2
Easy, dont you think ?
I need help with this . short and easy response please

Answers
Which conversions go from a smaller unit to a larger unit? Select all that apply.
centimeters to millimeters
decimeters to meters
hectograms to kilograms
liters to centiliters
Answers
Answer:
decimeters to meters
Step-by-step explanation:
There are 10 decimeters in a meter.
Answer:
decimeters to meters
hectograms to kilograms
Step-by-step explanation:
A chess player ran a simulation twice to estimate the proportion of wins to expect using a new game strategy. Each time, the simulation ran a trial of 1,000 games. The first simulation returned 212 wins, and the second simulation returned 235 wins. Construct and interpret 95% confidence intervals for the outcomes of each simulation.
A. The confidence interval from the first simulation is (0.187, 0.237), and the confidence interval from the second simulation is (0.209, 0.261). For the first trial, we are 95% confident the true proportion of wins with the new game strategy is between 0.187 and 0.237. For the second trial, we are 95% confident the true proportion of wins with the new game strategy is between 0.209 and 0.261.
B. The confidence interval from the first simulation is (0.187, 0.237), and the confidence interval from the second simulation is (0.209, 0.261). For the first trial, we are 90% confident the true proportion of wins with the new game strategy is between 0.187 and 0.237. For the second trial, we are 90% confident the true proportion of wins with the new game strategy is between 0.209 and 0.261.
C. The confidence interval from the first simulation is (0.191, 0.233), and the confidence interval from the second simulation is (0.213, 0.257). For the first trial, we are 95% confident the true proportion of wins with the new game strategy is between 0.191 and 0.233. For the second trial, we are 95% confident the true proportion of wins with the new game strategy is between 0.213 and 0.257.
D. The confidence interval from the first simulation is (0.191, 0.233), and the confidence interval from the second simulation is (0.213, 0.257). For the first trial, we are 90% confident the true proportion of wins with the new game strategy is between 0.191 and 0.233. For the second trial, we are 90% confident the true proportion of wins with the new game strategy is between 0.213 and 0.257.
Answers
The correct option regarding the 95% confidence interval for this problem is given as follows:
A. The confidence interval from the first simulation is (0.187, 0.237), and the confidence interval from the second simulation is (0.209, 0.261). For the first trial, we are 95% confident the true proportion of wins with the new game strategy is between 0.187 and 0.237. For the second trial, we are 95% confident the true proportion of wins with the new game strategy is between 0.209 and 0.261.
What is a confidence interval of proportions?A confidence interval of proportions has the bounds given by the rule presented as follows:
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which the variables used to calculated these bounds are listed as follows:
\(\pi\) is the sample proportion, which is also the estimate of the parameter.z is the critical value.n is the sample size.The confidence level is of 95%, hence the critical value z is the value of Z that has a p-value of \(\frac{1+0.95}{2} = 0.975\), so the critical value is z = 1.96.
The parameters for the first simulation are given as follows:
\(n = 1000, \pi = \frac{212}{1000} = 0.212\)
Hence the lower bound of the interval is of:
\(0.212 - 1.96\sqrt{\frac{0.212(0.788)}{1000}} = 0.187\)
The upper bound is of:
\(0.212 + 1.96\sqrt{\frac{0.212(0.788)}{1000}} = 0.237\)
For the second simulation, the parameters are given as follows:
\(n = 1000, \pi = \frac{235}{1000} = 0.235\)
Hence the lower bound of the interval is of:
\(0.235 - 1.96\sqrt{\frac{0.235(0.765)}{1000}} = 0.209\)
The upper bound is of:
\(0.235 + 1.96\sqrt{\frac{0.235(0.765)}{1000}} = 0.261\)
This means that option A is the correct option.
More can be learned about the z-distribution at https://brainly.com/question/25890103
#SPJ1
PLS HELP THIS IS MY FINAL

Answers
Answer: C. 25.6
Step-by-step explanation:
can you help me with this please

Answers
Answer:
a) y = 2 x - 1
b) y = - x + 7
c) y = 7 x + 2
Step-by-step explanation:
Use a pair of (x1, y1) and (x2, y2) points to find the equation of the line for each tables:
a) (5, 9) and (10, 19)
slope: (y2 - y1) / (x2 - x1) = (19 - 9) / (10 - 5) = 10 / 5 = 2
Then y = 2 x + b
solve for b in: 9 = 2 (5) + b
b = 9 - 10 = -1
Then y = 2 x - 1
b) (2, 5) and (5, 2)
slope: (y2 - y1) / (x2 - x1) = (2 - 5) / (5 - 2) = -3 / 3 = -1
Then y = - x + b
solve for b in: 5 = - (2) + b
b = 5 + 2 = 7
Then y = - x + 7
c) (3, 23) and (6, 44)
slope: (y2 - y1) / (x2 - x1) = (44 - 23) / (6 - 3) = 21 / 3 = 7
Then y = 7 x + b
solve for b in: 23 = 7 (3) + b
b = 23 - 21 = 2
Then y = 7 x + 2
Help me PLEASEEE I need help
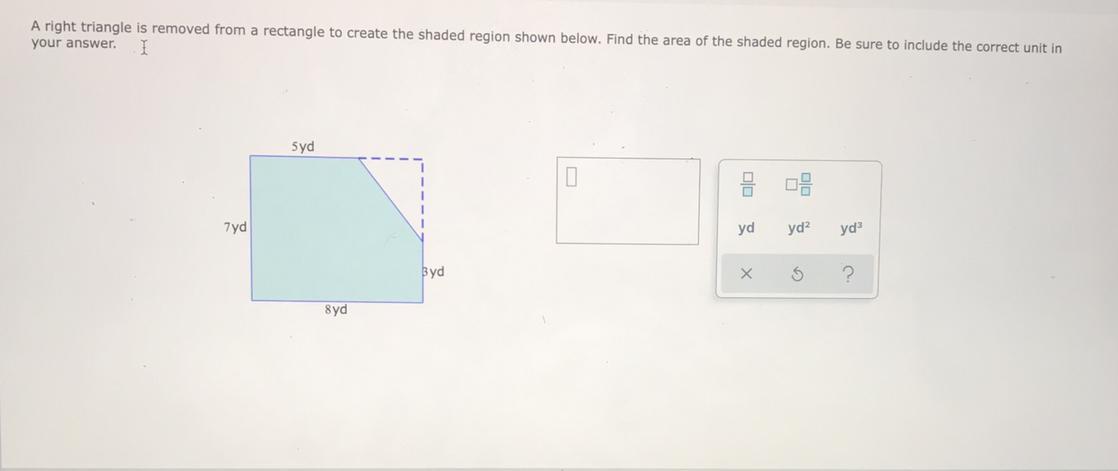
Answers
Answer:
area of shaded portion=56 - 1/2 ×3×4=56-6= 50 yd^2
adam is standing next tot he palmetto building in columbia, south carolina. he is 6 feet tall and the length of his shadow is 9 feet. if the length of the shadow of the building is 322.5 feet, how tallis the building?
Answers
He stands 6 feet tall, and his shadow extends 9 feet. if the building's shadow extends for 322.5 feet.
Now 6/9 = X/322.5
9X = 1935
X = 215ft
The Height of the building = 215ft
Consider an object AB of height h such that its shadow of length s is formed and angle of elevation is θ.
The object AB depicts a right triangle in which ∠ABO = 90o.
Now we know that in trigonometry, the tangent ratio for an angle is equal to the opposite side to that angle divided by its adjacent side.
So, for the angle of elevation θ, we have
=> tan θ = AB/OB
Putting AB = h and OB = s, we get
=> tan θ = h/s
=> s/h = 1/tan θ
=> s = h/tan θ
Learn more about Shadow here:
https://brainly.com/question/15021258
#SPJ4
is 50.11111111... a rational number answer fast ill give brainliest
Answers
Answer:
the answer is irrational