The base of a triangle with the height of 7 units is represented by the formula b=2/7a. the base of the triangle is less than 10. write and solve an inequality that represents the possible area a if the triangle.
Answers
The inequality that represents the possible area of the triangle is 2/7a < 10
The solution to the inequality is a < 35
Solving linear inequalitiesFrom the question, we are to write and solve an inequality that represents the possible area, a, of the triangle
From the given information,
The base of the triangle is given by
b = 2/7a
Also, from the given information,
The base of the triangle is less than 10
That is,
b < 10
Then,
we can write that
2/7a < 10
This is the inequality that represents the possible area of the triangle
Now, solve the inequality
2/7a < 10
Multiply both sides of the equation by 7/2
7/2× 2/7a < 7/2× 10
a < 7 × 5
a < 35
Hence, the inequality that represents the possible area of the triangle is 2/7a < 10
The solution to the inequality is a < 35
Learn more on Solving linear inequalities here: https://brainly.com/question/25275758
#SPJ1
Related Questions
1. Write an equation for the nth term of the Arithmetic sequence. Use the
Formula: an = a + (n - 1)d
2. Identify if the given sequence is Arithmetic, Geometric, or neither.
20, 15, 10, 5
Answers
Answer:
Step-by-step explanation:
Remark: This is an arithmetic sequence. Rather than going up, it is going down. Still it is an arithmetic sequence.
Givens
a1 = 20
d = -5
Formula
tn = a1 + (n-1)*-5 Remove the brackets
tn = 20 - 5n + 5
tn = 25 - 5n
So just to confirm it works, let n = 4 (which makes t4 = 5 as is given).
t4 = 25 - 5*4
t4 = 25 - 20
t4 = 5 which is exactly what t4 is
The population of Australia was 14.692 million in 1980 and 17.065 million in 1990. Estimate the population of Australia in 2000.
A. 10.89 million
B. 17.32 million
C. 19.82 million
D. 23.02 million
Answers
Answer:
C
Step-by-step explanation:
make y the subject of formula 2y=3x-2
Answers
Answer:
\(2y = 3x - 2 \\ y = \frac{3x - 2}{2} \\ y = \frac{3}{2} x - 1 \\ thank \: you\)
Answer:
y=3x-2÷2
Step-by-step explanation:
2y=3x-2
solution
cross multiple 2y=3x-2 and make y the subject of the formula,so y now is equal to 3x minus 2 divided by 2.Consider the following function f(x)=x4+3, x>=0.Find an explicit formula for f^-1
Answers
The explicit formula for f^-1 is (x-3)^(1/4) and this is obtained by switching the roles of x and y and solving for y in terms of x.
To find the inverse function of f(x)=x^4+3, we need to switch the roles of x and y, and solve for y.
Let y = x^4+3
Subtract 3 from both sides to get:
y - 3 = x^4
Take the fourth root of both sides to isolate x:
(x^4)^(1/4) = (y-3)^(1/4)
Simplify:
x = (y-3)^(1/4)
So the inverse function of f(x) is:
f^-1 (x) = (x-3)^(1/4)
This is the explicit formula for the inverse function of f(x).
To know more about explicit formula visit:
https://brainly.com/question/18069156
#SPJ11
Subtract. Write your answer as a mixed number in simplest form. 5 1/2 - 2 1/6
Answers
10/2+1/2 - 12/6+1/6. -> change the 5 and 6 to fractions
= 11/2 - 13/6. -> add up
= 33/6 -13/6. -> multiply the first fraction by 3 so.
that you have the same denominators
= 20/6. -> subtract
= 10/3
= 9/3 +1/3
= 3 1/3
Que expresan las desigualdades
Answers
espero que esto ayude ❤️
Express square root of 8 as a power of 2

Answers
Answer:
\(2^{\frac{3}{2} }\)
Step-by-step explanation:
note that 8 = 2³
and using the rule of exponents/ radicals
\(a^{\frac{m}{n} }\) = \(\sqrt[n]{a^{m} }\)
Thus
\(\sqrt{8}\) = \(\sqrt{2^{3} }\) = \(2^{\frac{3}{2} }\)
Expressing the square root of 8 as a power of 2, we would have to follow two steps.
Step 1: We find the square root of 8√8 = 2.8284271247
Step 2: We express the square root of 8 as a power of 2. We do this using the assumption method.Assumption 1
\(2^{1}\) = 2
Asumption 2
\(2^{1.2}\) = 2.29739671
Assumption 3
\(2^{1.5}\) = 2.8284271247
Therefore, the square of 8 as a power of 2 is \(2^{1.5}\)
To learn more, visit the link below:
https://brainly.com/question/2142771
Sergio has two similar cylindrical pots, Pot A and Pot B. The radius of Pot A is 15 inches, and the radius of Pot B is 3 inches. What is the ratio of the volume of Pot A to the volume of Pot B
Answers
The ratio of the volume of pot A to that of pot B = 25:1.
What is the volume of a cylinder?The volume of a cylinder having radius 'r' and height 'h', is equal to \(\pi r^{2} h\).
Given:
Height of pot A = Height of pot B = h (let)Radius of pot A = 15 inchesRadius of pot B = 3 inchesVolume of pot A = \(\pi (15)^{2}h=225\pi h\) = V1 (let)
Volume of pot B = \(\pi (3)^{2} h=9\pi h\) = V2 (let)
Then \(\frac{V1}{V2} = \frac{225\pi h}{9\pi h}=\frac{225}{9}=25\)
Hence, the ratio of volume of pot A to that of pot B is 25:1.
To learn more about the volume of a cylinder, refer to the link: https://brainly.com/question/23935577
#SPJ4
Find the distance between the two points. Write your answer as a
decimal rounded to the hundredths place if needed.
(3, -12) and (-7, -11)
Answers
The question is in the picture plz help

Answers
Answer:
B
Step-by-step explanation:
Answer: The Answer is A
Step-by-step explanation:
Match each fraction to a reasonable estimate
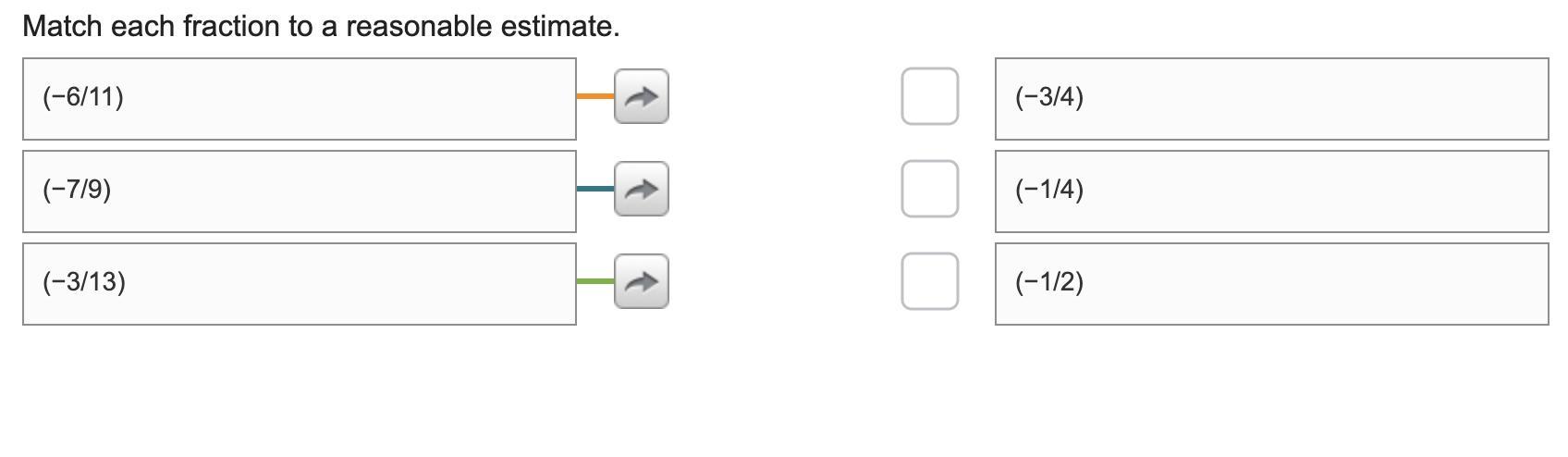
Answers
7/9 is about 3/4
3/13 is about 1/4
4x – 5 + 2(x – 3) = 12x + 7
X=
Answers
Answer:
-3
Step-by-step explanation:
4x - 5 + 2(x - 3) = 12x + 7
4x - 5 + 2x - 6 = 12x + 7
4x + 2x - 5 - 6 = 12x + 7
6x - 11 = 12x + 7
collect like terms
6x - 12x = 7 + 11
-6x = 18
-x = 3
x = -3
name the angle using three points

Answers
MÎA or AÎM
the point where the angle is has to be in the middle, but for the other two letters, you can choose which one goes where
How many ways are there to pick an (unordered) subset of 6 cards from a standard 52-card deck so that the subset contains at least one Ace, at least one King, at least Queen, and at least one Jack
Answers
In a standard 52-card deck, there are 20,358 ways to pick an (unordered) subset of 6 cards that contains at least one Ace, at least one King, at least one Queen, and at least one Jack.
Can you determine the number of ways to select a subset of 6 cards from a standard 52-card deck, ensuring that at least one Ace, King, Queen, and Jack are included?When selecting a subset of 6 cards from a standard 52-card deck, the main objective is to ensure that the subset contains at least one Ace, one King, one Queen, and one Jack. To calculate the number of ways this can be achieved, we can break it down into steps.
Step 1: Select one Ace, King, Queen, and Jack
There are 4 ways to choose one Ace, 4 ways to choose one King, 4 ways to choose one Queen, and 4 ways to choose one Jack.
Step 2: Select two additional cards from the remaining 48 cards
After selecting one Ace, one King, one Queen, and one Jack, we are left with 48 cards. To complete the subset of 6 cards, we need to choose two more cards from this remaining set. The number of ways to select two cards from 48 is calculated using combinations, denoted as "48 choose 2," which is equal to 1,128.
Step 3: Multiply the results
To determine the total number of ways, we multiply the results of each step. Therefore, the total number of ways to pick an (unordered) subset of 6 cards that contains at least one Ace, one King, one Queen, and one Jack is 4 * 4 * 4 * 4 * 1,128 = 20,358.
Learn more about combinations
brainly.com/question/30271591
#SPJ111
Find f: f"(x) = 8x³ + 5, f(1) = 0, f'(1) = 8
Answers
The value of f(x) is \(f(x) =\frac{2}{5}x^5+\frac{5}{2}x^{2} +x-\frac{39}{10}\)
Differential Equation:The equation in which the derivative of the given function is included is known as the differential equation. We have to find out a particular solution to the given ODE. We will use the power rule of integration to solve this question.
We have the function :
f"(x) = \(8x^3+5\)
Integrate on both sides with respect to x.
\(f'(x) = 8\int\limits x^3dx + \int\limits 5dx\\\\f'(x) = 2x^4+5x+C_1\)
Integrate on both sides with respect to x.
\(f(x) = 2\int\limitsx^4dx+5\int\limits xdx+\int\limits C_1dx\\\\f(x) = \frac{2}{5}x^5+\frac{5}{2}x^2+C_1x+C_2\\ \\\)
f'(1) = 8
8 = 2 + 5 + \(C_1\)
\(C_1=0\)
f(1) =0
\(0 = \frac{2}{5} +\frac{5}{2}+1+C_2\\ \\C_2=-\frac{39}{10\\}\\\)
\(f(x) =\frac{2}{5}x^5+\frac{5}{2}x^{2} +x-\frac{39}{10}\)
Learn more about Differential equation at:
https://brainly.com/question/31583235
#SPJ4
(Can someone please help me with this math test will give you brainlist and all my points please and thank you!)The common ratio of a geometric sequence is 3/2 the first term of the sequence is -2. What is the second term of the sequence

Answers
Answer:
Step-by-step explanation:
first term = a=-2
second term= ar=-2*(3/2)=-3
hope this helps
hope im not so late
Suppose you borrowed $45,000 at a rate of 8.5% and must repay it in 5 equal installments at the end of each of the next 5 years. By how much would you reduce the amount you owe in the first year? Select the correct answer. a. $7,594.46 b. $7,600.46 c. $7,618.46 d. $7,612.46 e. $7,606.46
Answers
The correct answer is option a. $7,594.46.
To calculate the amount you would reduce the amount you owe in the first year, we can use the formula for the equal installment of a loan. The formula is:
Installment = Principal / Number of Installments + (Principal - Total Repaid) * Interest Rate
In this case, the principal is $45,000, the number of installments is 5, and the interest rate is 8.5%.
Let's calculate the amount you would reduce the amount you owe in the first year:
Installment = $45,000 / 5 + ($45,000 - $0) * 0.085Installment = $9,000 + $3,825
Installment = $12,825
Therefore, you would reduce the amount you owe by $12,825 in the first year.The correct answer is option a. $7,594.46.
Learn more about compound angle here:
https://brainly.com/question/33061695
#SPJ8
or Precalculus
Unit: Get ready for trigonometry
x
Unit test
f is a trigonometric function of the form f(x) = a cos(bx + c) + d.
Below is the graph of f(x). The function has a maximum point at (pi, 9) and a minimum point at
(3pi/4, 1)
Find a formula for f(x). Give an exact expression.
Answers
Answer:
4cos(4x-4pi)+5
Step-by-step explanation:
It was from khan
Somebody help plz!!!

Answers
Answer:
42°
Step-by-step explanation:
angle b is complementary to 48° so their sum is 90°.
Answer:
42
Step-by-step explanation:
48 + b = 90
90 - 48 = 42
b = 42
3u+3-2(-3u-1)=5(u-1)
Answers
Answer:
u = -1/5
Step-by-step explanation:
name me brainliest please.
a) Find the 50 th derivative of y=cos2x
Answers
To find the 50th derivative of y = cos(2x), we can use the power rule and trigonometric identities. The pattern of derivatives of cosine function allows us to determine the general form of the 50th derivative. The 50th derivative of y = cos(2x) is given by (-2)^25 * cos(2x), where (-2)^25 represents the alternating sign pattern for even derivatives.
The derivative of y = cos(2x) can be found by applying the chain rule. The derivative of cos(u) with respect to u is -sin(u), and the derivative of u = 2x with respect to x is 2. Thus, the derivative of y = cos(2x) is:
dy/dx = -sin(2x) * 2 = -2sin(2x)
The second derivative can be found by differentiating the first derivative:
d²y/dx² = d/dx (-2sin(2x)) = -4cos(2x)
Similarly, we can continue differentiating to find the third, fourth, and subsequent derivatives. By observing the pattern, we can notice that even derivatives of cosine functions have a pattern of alternating signs, while the odd derivatives have a pattern of alternating signs with a negative sign.
For the 50th derivative, we have an even derivative. The pattern of alternating signs for even derivatives implies that the 50th derivative will have a positive sign. Additionally, since the derivative of cos(2x) is -2sin(2x), the 50th derivative will have (-2)^25 * cos(2x), where (-2)^25 represents the alternating sign pattern for even derivatives.
Therefore, the 50th derivative of y = cos(2x) is (-2)^25 * cos(2x), indicating that the 50th derivative has a positive sign.
Learn more about derivatives here:
brainly.com/question/25324584
#SPJ11
a continuous random variable x has a normal distribution with a mean of 12.25. the probability that x takes a value less than 13 is 0.82. Use this information and the symmetry of the density function to find the probability that X
takes a value greater than 11.50
Sketch the density curve with relevant regions shaded to illustrate the computation.
Answers
Given that a continuous random variable x has a normal distribution with a mean of 12.25 and the probability that x is less than 13 is 0.82, we can use the symmetry of the density function to find the probability that x is greater than 11.50.
Since the normal distribution is symmetric, the probability of x being less than 13 is equivalent to the probability of x being greater than the mean minus 13. Therefore, P(x < 13) = P(x > 12.25 - 13).
To find the probability that x is greater than 11.50, we can use the same reasoning. We know that the probability of x being less than 11.50 is equivalent to the probability of x being greater than the mean minus 11.50. Therefore, P(x < 11.50) = P(x > 12.25 - 11.50).
To illustrate the computation, we can sketch the density curve of the normal distribution with the relevant regions shaded. The mean, 12.25, is the center of the distribution. We shade the region to the left of 13, representing P(x < 13), and shade the region to the right of 11.50, representing P(x > 11.50). By using the symmetry of the density function, we can see that the shaded region to the right of 11.50 is equal to the shaded region to the left of 13.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
I need help on in the answer to this question

Answers
Notice that angle z and the angle with measure 70⁰ is a linear pair. Hence, it follows that they are supplementary (they'll sum up to 180⁰):
\(z+70^{\circ}=180^{\circ}\)Solve for z in the equation:
\(\begin{gathered} z=180^{\circ}-70^{\circ} \\ \Rightarrow z=110^{\circ} \end{gathered}\)Using the Angles formed by two intersecting chords theorem: If two chords intersect inside a circle, then the measure of the angle formed is one-half the sum of the measure of the arcs intercepted by the angle and its vertical angle , it follows that:
\(z=\frac{1}{2}(w+79^{\circ})\)Substitute z=110⁰ into the equation and solve for w:
\(\begin{gathered} 110^{\circ}=\frac{1}{2}(w+79^{\circ}) \\ \text{Cross multiply:} \\ \Rightarrow2\times110^{\circ}=w+79^{\circ} \\ \Rightarrow220^{\circ}=w+79^{\circ} \\ \Rightarrow w=220^{\circ}-79^{\circ} \\ \Rightarrow w=141^{\circ} \end{gathered}\)The value of w is 141.
Jennifer opened a savings account with $750. She earned $75 in interest after 2 years. What is the interest rate?
Answers
Answer:
5%
Step-by-step explanation:
Solving our equation
r = 75 / ( 750 × 2 ) = 0.05
r = 0.05
converting r decimal to a percentage
R = 0.05 * 100 = 5%/year
The interest rate required to
accumulate simple interest of $ 75.00
from a principal of $ 750.00
over 2 years is 5% per year.
Parker is planning to build a playhouse for his sister.The scale model below gives the reduced measures for width and height. The width of the playhouse is 22 centimeters and the height is 10 centimeters. Not drawn to scale The yard space is large enough to have a playhouse that has a width of 3.5 meters. If Parker wants to keep the playhouse in proportion to the model, what cross multiplication of the proportion should he use to find the height
Answers
Answer:
\(10 \times 3.5 = 22x\)
Step-by-step explanation:
It is given that:
Parker wishes to construct a \(\text{playhouse}\) for his sister. The width and the height of the house is not scaled to the yard space.
So the width of the play house = 22 centimeters
The height of the play house = 10 centimeters
Bu the space in the \(\text{yard is large}\) enough that a play house can be constructed so that it have a width of \(3.5\) meters.
So the cross multiplication of the proportion that parker uses to find the height of the playhouse is given by : \(10 \times 3.5 = 22x\)
Answer:
The answer is C, (10) (3.5) = 22 x
Hope this helped!
P. S. : Can I get brainliest please?
1-x/11 \(1-x/11 =6\\\)=6
Answers
Given:
Consider the equation is:
\(\dfrac{1-x}{11}=6\)
To find:
The value of x.
Solution:
We have,
\(\dfrac{1-x}{11}=6\)
After multiplying both sides by 11, we get
\(1-x=66\)
\(-x=66-1\)
\(-x=65\)
Multiply both sides by -1.
\(x=-65\)
Therefore, the value of x is -65.
QUANTO É 38-39???
E POR QUE???
Answers
Answer:
-1
Step-by-step explanation:
negative 1
HELPPPPPPPP PLEASEEEEEEE!!!!!!!

Answers
Answer:
false
Step-by-step explanation:
it's false negative
Which expression can be used to find the zeros of the function f(x) = 4x2 + 2x - 12?
Answers
Answer:
x=-2 and x=-12
(-12,-2)
A beverage company wants to manufacture a new juice with a mixed flavor, using only orange and pineapple flavors. Orange flavor contains 5% of vitamin A and 2% of vitamir C. Pineapple flavor contains 8% of vitamin C. The company's quality policies indicate that at least 20 L of orange flavor should be added to the new juice and vitamin C content should not be greater than 5%. The cost per liter of orange flavor is $1000 and pineapple flavor is $400. Determine the optimal amount of each flavor that should be used to satisfy a minimum demand of 100 L of juice. A) A linear programming model is needed for the company to solve this problem (Minimize production cost of the new juice) B) Use a graphic solution for this problem C) What would happen if the company decides that the juice should have a vitamin C content of not greater than 7% ?
Answers
A beverage company has decided to manufacture a new juice with mixed flavors, which is prepared from orange and pineapple. The vitamin contents are 5% of vitamin A and 2% of vitamin C in the orange flavor, while pineapple flavor contains 8% of vitamin C.
The company's policies are to add at least 20 L of orange flavor to the new juice and limit the vitamin C content to no more than 5%. The cost of orange flavor is $1000 per liter, while the cost of pineapple flavor is $400 per liter.To satisfy a minimum demand of 100 L of juice, we must determine the optimal amount of each flavor to use.A) A linear programming model is needed for the company to solve this problem (Minimize production cost of the new juice)B) Use a graphic solution for this problem.The objective function of the optimization problem can be given as:min C = 1000x + 400yThe constraints that the company has are,20x + 0y ≥ 100x + y ≤ 5x ≥ 0 and y ≥ 0The feasible region can be identified by graphing the inequality constraints on a graph paper. Using a graphical method, we can find the feasible region, and by finding the intersection points, we can determine the optimal solution.The graph is shown below; The optimal solution is achieved by 20L of orange flavor and 80L of pineapple flavor, as indicated by the intersection point of the lines. The optimal cost of producing 100 L of juice would be; C = 1000(20) + 400(80) = $36,000.C) If the company decides that the juice should have a vitamin C content of no more than 7%, it would alter the problem's constraints. The new constraint would be:x + y ≤ 7Dividing the equation by 100, we obtain;x/100 + y/100 ≤ 0.07The objective function and the additional constraint are combined to create a new linear programming model, which is solved graphically as follows: The feasible region changes as a result of the addition of the new constraint, and the optimal solution is now achieved by 20L of orange flavor and 60L of pineapple flavor. The optimal cost of producing 100 L of juice is $28,000.
In conclusion, the optimal amount of each flavor that should be used to satisfy a minimum demand of 100 L of juice is 20L of orange flavor and 80L of pineapple flavor with a cost of $36,000. If the company decides that the juice should have a vitamin C content of no more than 7%, the optimal amount of each flavor is 20L of orange flavor and 60L of pineapple flavor, with a cost of $28,000.
To learn more about optimal cost visit:
brainly.com/question/32634756
#SPJ11