Answers
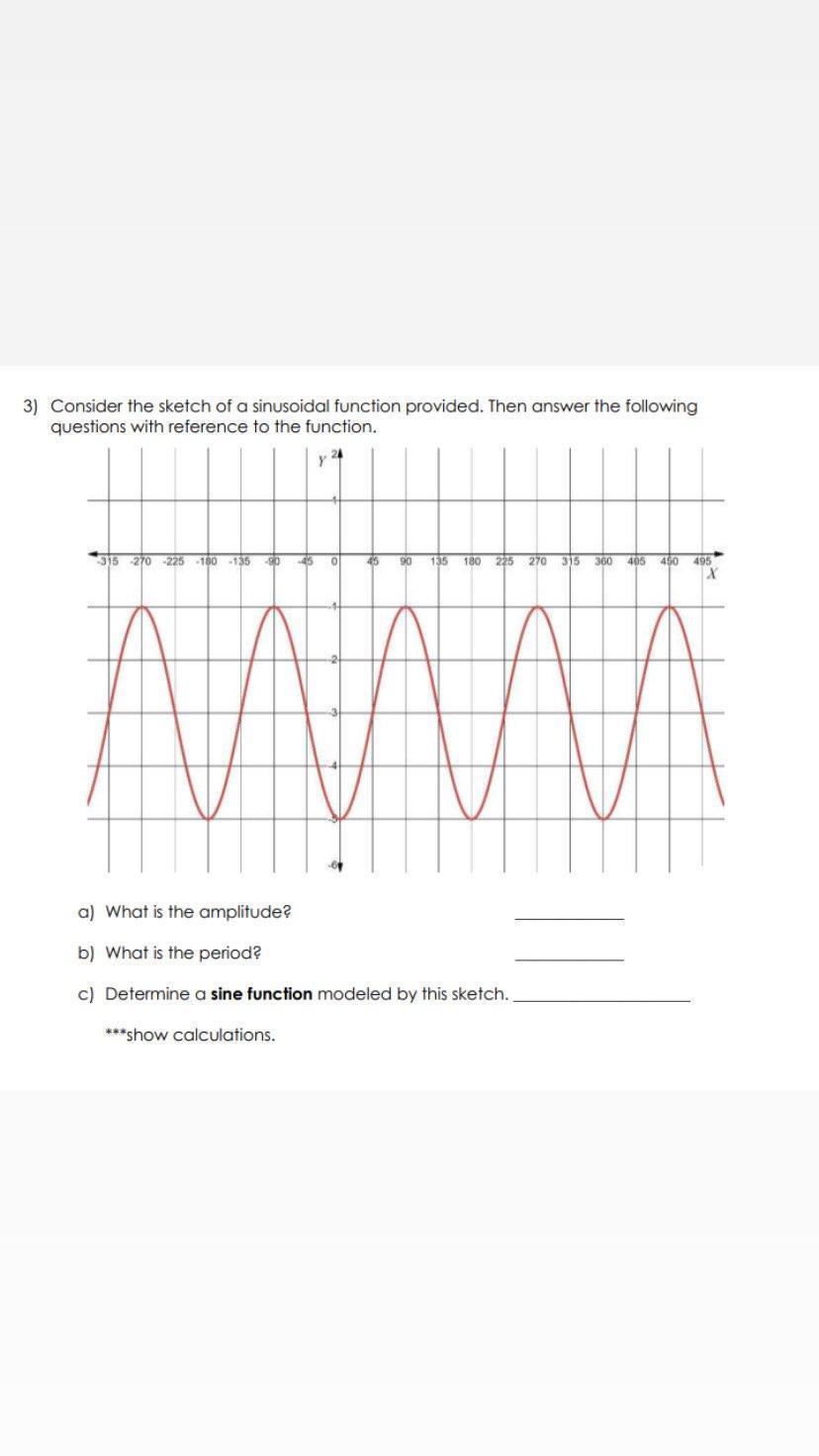
Given: The sine graph shown in the image
To Determine: The amplitude, the period and the sine function
Solution
The general sine function is as shown below
From the given graph,
The amplitude is
\(\begin{gathered} A=2 \\ Period=270^0-90^0=180^0 \\ Period=\frac{2\pi}{B} \\ \pi=180^0 \\ 180^0=\frac{2\times180^0}{B} \\ B\times180^0=360^0 \\ B=\frac{360^0}{180^0} \\ B=2 \end{gathered}\)\(\begin{gathered} C=phase(shift)=-45^0 \\ D=-3 \end{gathered}\)So, the function of the graph would be
\(\begin{gathered} y=Asin(B(x+C))+D \\ A=2 \\ B=2 \\ C=-45^0 \\ D=-3 \end{gathered}\)\(\begin{gathered} f(x)=2sin(2(x-45^0)-3 \\ f(x)=2sin(2x-90^0)-3 \end{gathered}\)\(\begin{gathered} OR \\ f(x)=2sin(2x-\frac{\pi}{2})-3 \end{gathered}\)Hence, the sine function of the given graph is
y = 2sin(2x - 90⁰) - 3
OR
y = 2sin(2x - π/2) - 3


Related Questions
a certain number is written on the blackboard. One student increased that number by 23, and the other decreased it by 1. It turned out that the result of the first one is 7 times greater than the result of the second one. What number was written on the blackboard?
Answers
The number written on the board will be negative 27. This can be solved by using the concept of algebra.
What is Algebra?Algebra is the study of mathematical symbols, while logic is the manipulation of those symbols.
Let x be the number.
There is a number written on the board. One student increased the number by 23. Then the first number will be
⇒ x + 23
But another student decreased the same number by 1. Then the second number will be
⇒ x - 1
The first student's result was 7 times greater than the result of the second student.
7 first number = second number
or, 7(x + 23) = x - 1
or, 7x + 161 = x - 1
or, 6x = - 162
or, x = - 27
The number written on the board will be negative 27.
To learn more about the Algebra refer to:
brainly.com/question/953809
#SPJ1
Help pleaseeeeeeeeeeeeww

Answers
Answer:
1: Shifted 5 units right
2: Shifted 1.8 units left
Step-by-step explanation:
XPO Corporation has a minimum tax credit of $51,000 from 2017. XPO’s 2018 tax liability before any MTC carryover is $30,500. What is XPO’s minimum tax credit carryover to 2019, if any?
Answers
XPO's minimum tax credit carryover to 2019 is $20,500.
What is Algebraic expression ?
Algebraic expression can be defined as combination of variables and constants. An algebraic expression is a mathematical phrase that can contain numbers, variables, and mathematical operations such as addition, subtraction, multiplication, and division.
XPO's minimum tax credit from 2017 is $51,000. This means that they are allowed to reduce their 2018 tax liability by up to $51,000 using this credit.
Since their 2018 tax liability before any MTC carryover is $30,500, they have not used the entire minimum tax credit for 2017. Therefore, they can carry over the remaining credit to 2019.
To calculate the minimum tax credit carryover to 2019, we need to subtract the amount of the minimum tax credit that XPO used in 2018 from the total minimum tax credit of $51,000:
Minimum tax credit carryover = $51,000 - $30,500 = $20,500
Therefore, XPO's minimum tax credit carryover to 2019 is $20,500.
To learn more about Algebraic expression from given link.
brainly.com/question/28884894
#SPJ1
A certain type of kickboard scooter comes in silver, red, 2
or purple with wheel sizes of 125 millimeters or 180
millimeters. Determine the total number of color-wheel size combinations.
(This is probability and I’m having such a hell of a time figuring it out pls help)
Answers
There are a total of 8 color-wheel size combinations for the kickboard scooter. This means that customers have 8 different options to choose from when selecting the color and wheel size for their scooter.
To determine the total number of color-wheel size combinations for the kickboard scooter, we need to multiply the number of color options by the number of wheel size options.
Given that there are 4 color options (silver, red, blue, and purple) and 2 wheel size options (125mm and 180mm), we can use the multiplication principle to find the total number of combinations:
Total combinations = Number of color options × Number of wheel size options
Total combinations = 4 colors × 2 wheel sizes
Total combinations = 8
There are a total of 8 color-wheel size combinations for the kickboard scooter. This means that customers have 8 different options to choose from when selecting the color and wheel size for their scooter.
For more such questions on combinations
https://brainly.com/question/28065038
#SPJ8
If you divided a rectangle into ten smaller rectangles and then each of THOSE into ten, each of the smallest rectangles is:
Answers
Find x when () = 2. Please explain step by step

Answers
Answer: Ans is 990. First such a number is 5×0 +2=2, then 5×1 +2=7, like that in all 20 numbers are there from 2 to 97 in A.P.with common difference of 5.
Step-by-step explanation:
Question 7, pre calc, include the answer in bold please. I have bad WiFi so please finish question if I get disconnected so I can see it, thanks
Answers
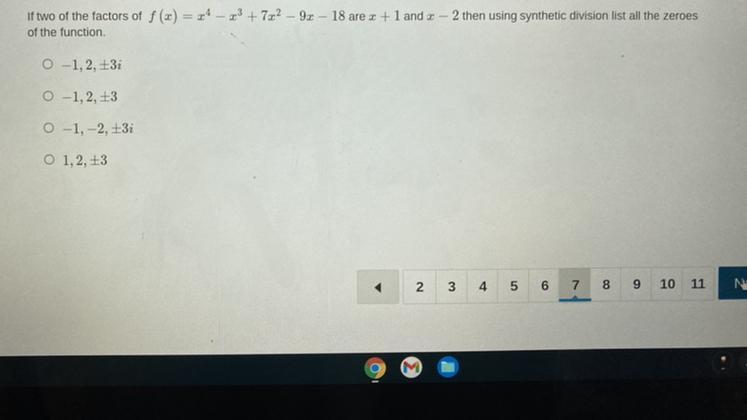
Given the following function
\(f(x)=x^4-x^3+7x^2-9x-18\)We want to find its roots. Since we already know that (x + 1) and (x - 2) are factors of this polynomial, we can divide our polynomial by those factors and factorize the result to get the other roots.
Let's start by dividing by the first factor
\(\frac{x^4-x^3+7x^2-9x-18}{x+1}\)To divide a polynomial by other, we start by dividing the leading term of the dividend by the leading term of the divisor(this will be the first term of our result)
\(\frac{x^4}{x}=x^3\)Then, we ultiply it by the divisor
\(x^3(x+1)=x^4+x^3\)Subtracting this result from the dividend, we have
\((x^4-x^3+7x^2-9x-18)-(x^4+x^3)=-2x^3+7x^2-9x-18\)This means that our division is
\(\frac{x^4-x^3+7x^2-9x-18}{x+1}=x^3+\frac{-2x^3+7x^2-9x-18}{x+1}\)Repeating the whole process of division with the second term, we have
\(\begin{gathered} x^3+\frac{-2x^3+7x^2-9x-18}{x+1}=x^3-2x^2+\frac{9x^2-9x-18}{x+1} \\ \Rightarrow\frac{x^4-x^3+7x^2-9x-18}{x+1}=x^3-2x^2+9x-18 \end{gathered}\)From this result, we can rewrite our function as
\(x^4-x^3+7x^2-9x-18=(x+1)(x^3-2x^2+9x-18)\)Repeating this same process with the other know factor, the other division we have to solve is
\(\frac{(x^3-2x^2+9x-18)}{x-2}=x^2+9\)Then, our function is
\(f(x)=(x^4-x^3+7x^2-9x-18)=(x+1)(x-2)(x^2+9)\)Then, to find the roots we need to solve the following equation
\((x+1)(x-2)(x^2+9)=0\)Since we have a product of 3 terms, the result will be zero if and only if one of the terms is zero. This means that the roots can be found by assuming each one is zero. The solutions for this equation are the same solutions for the following system
\(\begin{cases}x+1=0 \\ x-2=0 \\ x^2+9=0\end{cases}\Rightarrow\begin{cases}x=-1 \\ x=2 \\ x=\pm\sqrt[]{-9}=\pm3i\end{cases}\)And those are the roots for our function. x = -1, 2, +-3i.
What’s an equivalent expression to 3/5 - 13/5
Answers
Answer:
-2
Step-by-step explanation:
I am struggling to find domain and range please help thank you

Answers
Answer:
Domain: 0, 1, 2, 3, 4,
Range: 1, 2, 3, 4, 5,
Step-by-step explanation:
Based on the graph the domain of the function is 0, 1, 2, 3, 4, and the range is 1, 2, 3, 4, 5, therefore, the answer is:
Solve the following logarithmic equation.

Answers
I suppose this is the correct answer.
What’s a good estimate for 2,745 x 6.9? Show how you got you estimate.
Answers
Answer:
21000
Step-by-step explanation:
2745 -> 3000
6.9 -> 7
3000 x 7 =
21000
What is the area of this rectangle? Rectangle with width 5.1 cm and height 11.2 cm. Responses 16.3 cm2 16.3 cm, 2 32.6 cm2 32.6 cm, 2 57.12 cm2 57.12 cm, 2 571.2 cm2

Answers
The area of a rectangle with a width of 5.1 cm and a height of 11.2 cm is 57.12 cm².
To find the area of a rectangle, we multiply its length by its width. In this case, the width is given as 5.1 cm and the height (or length) is given as 11.2 cm.
Area = length × width
Area = 11.2 cm × 5.1 cm
Calculating the product, we get:
Area = 57.12 cm²
Therefore, the area of the rectangle is 57.12 cm².
The correct answer is: 57.12 cm².
It is important to note that when calculating the area of a rectangle, we should always include the appropriate unit of measurement (in this case, cm²) to indicate that we are dealing with a two-dimensional measurement. The area represents the amount of space covered by the rectangle's surface.
So, the area of a rectangle with a width of 5.1 cm and a height of 11.2 cm is 57.12 cm².
for more such question on rectangle visit
https://brainly.com/question/2607596
#SPJ8
Jamaica Cane Products has a fixed cost of $10,000 this period. Its direct labor is $1.50 per unit, and material is $0.75 per unit. The selling price is $4.00 per unit. Calculate the break-even point in dollars and the amount of units needed to break-even.
Answers
The break-even point in dollars is $22,857.14
The break-even point in units is 5,714
What is break-even point in dollars?
Break-even point in dollars is the amount of sales required for the firm to achieve a zero profit, I mean such that total revenue is the same as the total costs.
The break-even point in dollars can be determined as the fixed costs divided by the contribution margin ratio
In the case, the fixed costs is $10,000 whereas the contribution margin ratio is the contribution as a percentage of the sales price
contribution=sales price-variable costs
sales price=$4.00
variable costs=material cost+ labor cost
variable costs=$1.50+$0.75
variable costs=$2.25
contribution=$4.00-$2.25
contribution=$1.75
contribution margin ratio=contribution/sales price
contribution margin ratio=$1.75/$4.00
contribution margin ratio=43.75%
Break-even point in dollars=fixed costs/contribution margin ratio
Break-even point in dollars=$10,000/43.75%
Break-even point in dollars=$22,857.14
Break-even point in units=Break-even point in dollars/sales price
Break-even point in units=$22,857.14/$4.00
Break-even point in units=5,714 units
Find out more about break-even point on:https://brainly.com/question/9212451
#SPJ1
What is the circumference of this circle?

Answers
Answer:
18.16 km
Step-by-step explanation:
r = 2km so i took each circle there is 4 circle's and i multiplied each circle by 2 that's how i got the answer -.-
Answer:
12.56 km
Step-by-step explanation:
It's 12.56 km because the radius is 2 km, so...
2 * 2=4
(because that is just half)
4 * pi = 12.56
this graph shows data related to a company's stock price and time. which type of function best models data? A. a linear function with a positive slope
B. a square root function
C. a quadratic function with a negative value of a
D. a quadratic function with a positive value of a
Answers
Answer:
C. a quadratic function with a negative value of a
Step-by-step explanation:
It is likely that a quadratic function with a negative value of a would be the best model for this data, as it would represent a parabolic shape that can accommodate a downward trend, followed by an upward trend, in the stock price. The value of "a" determines the direction of the parabola, with a negative value resulting in a downward-facing parabola, which is appropriate for a stock price that starts low and increases over time. This type of function would provide a good fit for the data, especially if there are fluctuations or ups and downs in the stock price over time.
560/17 participate in a football tournament if each team plays against every other team ones, how many matches will be played tota
Answers
According to the information, it can be inferred that the total matches that would be played in total are 160,461.
What is a mathematical combination?A combination is a term to refer to an arrangement of elements in no particular order. For example:
When we put together a sandwich with salami, ham and turkey. The order in which the deli meats are placed does not matter as long as they are in a sandwich. There is only one way to stack the meat on the sandwich when the order doesn't matter.
How to calculate how many matches will be played in total?To calculate how many matches will be played in total we have to perform the following procedure:
\(= ^{567} C_{2} \\= \frac{(567)!}{2!565!} \\= \frac{567 * 566 * (565)!}{2 * (565)!} \\= 567 * 283\\= 160,461\\\\\)
As we can see after the combination, the number of games that would be played in this tournament would be 160,461.
Learn more about combination in: https://brainly.com/question/20211959
#SPJ1
what is the Y-intercept of the graph below.

Answers
Answer:
2
Step-by-step explanation:
the line meets the y axis at (0,2)
Answer:
you need this ?
the y is
y=-x+2
How can you fit data into a pictogram?
Answers
Answer:
Step-by-step explanation:
In a pictogram, data can be arranged as follows:
The organization is given in a Cartesian plane, with a vertical and a horizontal axis, images can be introduced. An independent variable is placed on the horizontal axis, usually small numbers. The dependent variable can be placed on the vertical axis, they are usually larger numbers.
NO LINKS!!
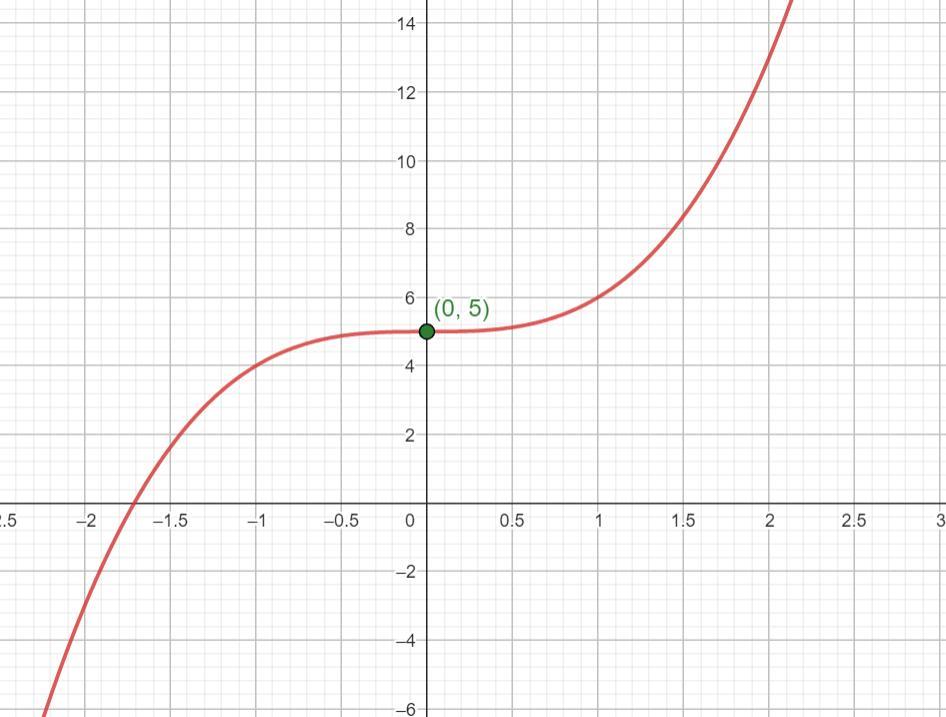
Consider the following equation.
y = x^3 + 5
Test for symmetry. (select all that apply)
1. x-axis symmetry
2. y-axis symmetry
3. origin symmetry
4. no origin symmetry
Graph the equation.
Answers
Answer:
4. no origin symmetry-----------------------------
Given function:
y = x³ + 5Graph it first (see attached).
Test the graph for symmetry.
We know the odd degree parent function y = x³ has an origin symmetry, whilst even degree functions may have axis symmetry.
The given function is a translation of cubic function 5 units up so the center of symmetry has translated as well. Therefore correct answer is 4.
Answer:
4. no origin symmetry
Step-by-step explanation:
Functions are symmetric with respect to the x-axis if for every point (a, b) on the graph, there is also a point (a, −b) on the graph:
f(x, y) = f(x, −y)To determine if a graph is symmetric with respect to the x-axis, replace all the y's with (−y). If the resultant expression is equivalent to the original expression, the graph is symmetric with respect to the x-axis.
\(\begin{aligned}&\textsf{Given}: \quad &y &= x^3 + 5\\&\textsf{Replace $y$ for $(-y)$}: \quad &-y &= x^3 + 5\\&\textsf{Simplify}: \quad &y &= -x^3 - 5\end{aligned}\)
Therefore, since the resultant expression is not equivalent to the original expression, it is not symmetric with respect to the x-axis.
--------------------------------------------------------------------------------------------------
Functions are symmetric with respect to the y-axis if for every point (a, b) on the graph, there is also a point (-a, b) on the graph:
f(x, y) = f(-x, y)To determine if a graph is symmetric with respect to the x-axis, replace all the x's with (−x). If the resultant expression is equivalent to the original expression, the graph is symmetric with respect to the y-axis.
\(\begin{aligned}&\textsf{Given}: \quad &y&=x^3+5\\&\textsf{Replace $x$ for $(-x)$}: \quad &y&=(-x)^3+5\\&\textsf{Simplify}: \quad &y&=-x^3+5\end{aligned}\)
Therefore, since the resultant expression is not equivalent to the original expression, it is not symmetric with respect to the y-axis.
--------------------------------------------------------------------------------------------------
Functions are symmetric with respect to the origin if for every point (a, b) on the graph, there is also a point (-a, -b) on the graph:
f(x, y) = f(-x, -y)To determine if a graph is symmetric with respect to the origin, replace all the x's with (−x) and all the y's with (-y). If the resultant expression is equivalent to the original expression, the graph is symmetric with respect to the origin.
\(\begin{aligned}&\textsf{Given}: \quad &y&=x^3+5\\&\textsf{Replace $x$ for $(-x)$ and $y$ for $(-y)$}: \quad &(-y)&=(-x)^3+5\\&\textsf{Simplify}: \quad &-y&=-x^3+5\\&&y&=x^3-5\end{aligned}\)
Therefore, since the resultant expression is not equivalent to the original expression, it is not symmetric with respect to the origin.

The images below show a picture of ricoffy tin container with no dimensions indicated.the container is 2,5 times smaller than what it is in reality. Measure the diameter of the tin in mm and write down the real diameter in mm
Answers
The diameter of the tin in the picture is \(3d/5\) where 'd' is the diameter of the tin in reality.
What is the measurement of the diameter?Determining the diameter of tin:
Since there is no indication of dimensions, represent the diameter with a variable 'd' and find the diameter of the tin according to the given condition in the problem.
Here we have assumed that the diameter of the tin is 'd' in reality and the diameter of the tin picture can be calculated as given below.
Here we have
A ricoffy tin container with no dimensions indicated
Let d and h be the diameter and height of the tin
Given that the container is 2/5 times smaller than d
then the diameter of the tin in the picture \(= d - 2/5(d)\)
\(= [5d - 2d]/5 = 3d/5\)
Therefore, The diameter of the tin in the picture is \(3d/5\) where 'd' is the diameter of the tin in reality.
Learn more about diameter here:
https://brainly.com/question/5501950
#SPJ1
Evaluate the two expressions below to decided if they are equivalent to each other. Write Yes or No when stating if they are equivalent.

Answers
According to the solving they are not equivalent expression:
Expression 1: 4y(y +20) ≠ Expression 2: 4y + 24.
What would the inverse of it be?Expressions that appear to be equivalent do the same action despite having distinct appearances. When the variable is input with the same value, two equivalent algebraic formulas are given the same value.
What does a math inverse mean?An inverse in mathematics is a function that "undoes" another function. In other words, if f(x) produces y, then y entered into the inverse of f produces x. An invertible function is one that has an inverse, and the inverse is indicated by the symbol f1.
According to the given information:
Expression 1: 4y(y +20)
Expression 2: 4y + 24
While putting the value in first expression:
For expression 1:
= 4y(y +20)
= 8(2 + 20)
= 8 x 22
= 176
For expression 2:
= 4y + 24
= 8 + 24
= 32
They are not equivalent expression:
To know more about equivalent expression visit:
brainly.com/question/28170201
#SPJ1
A factory uses a special kind of lubricant to maintain its four milling machines. The weekly lubricant usage for each machine can be approximated with a normal distribution. This distribution has a mean of 30 gallons and a standard deviation of 11.5 gallons, and it can be considered as an independent random variable (zero covariance, zero correlation) from machine to machine. Suppose at the beginning of the week, the factory has a total of 150 gallons of lubricant in stock. The factory will not receive any replenishment of lubricant from its supplier until the end of the week.Assume that the total lubricant usage (four machines combined) also follows a normal distribution.
Required:
What is the probability that the factory will run out of lubricant before the next replenishment arrives?
Answers
Answer:
0.0968 = 9.68% probability that the factory will run out of lubricant before the next replenishment arrives
Step-by-step explanation:
When the distribution is normal, we use the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
This distribution has a mean of 30 gallons and a standard deviation of 11.5 gallons
Since there are four machines, we have that:
\(\mu = 30*4 = 120\)
\(\sigma = 11.5\sqrt{4} = 11.5*2 = 23\)
What is the probability that the factory will run out of lubricant before the next replenishment arrives?
More than 150 gallons, so this is 1 subtracted by the pvalue of Z when X = 50.
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{150 - 120}{23}\)
\(Z = 1.3\)
\(Z = 1.3\) has a pvalue of 0.9032
1 - 0.9032 = 0.0968
0.0968 = 9.68% probability that the factory will run out of lubricant before the next replenishment arrives
A fence with 2 gates in it surrounds a lion enclosure.
Each gate is 4 m wide.
an image
What is the length of the fence around the enclosure not including the gates?
Answers
The length of the fence around the enclosure not including the gates is:2l + 2w + 8 m
To find the length of the fence around the enclosure, we need to first find the perimeter of the rectangle and then subtract the combined length of the two gates from it.
Let's assume the length of the rectangle is 'l' and the width is 'w'.
From the given data, we know that each gate is 4 m wide.
Therefore, the width of the rectangle is:
Width = w + (4 m + 4 m) = w + 8 m
The perimeter of the rectangle is:
P = 2l + 2(w + 8 m) = 2l + 2w + 16 m
Now, we need to subtract the combined length of the two gates from the perimeter:
P - 2 × 4 m = 2l + 2w + 16 m - 8 m = 2l + 2w + 8 m
So, the length of the fence around the enclosure not including the gates is:2l + 2w + 8 m
For such more questions on length
https://brainly.com/question/28108430
#SPJ8
All boxes with a square base, an open top, and a volume of 220 ft cubed have a surface area given by S(x)equalsx squared plus StartFraction 880 Over x EndFraction , where x is the length of the sides of the base. Find the absolute minimum of the surface area function on the interval (0,infinity). What are the dimensions of the box with minimum surface area?
Answers
Answer:
Length of the sides of the base (x) = 7.606 ft
Height (h) = 3.802 ft
The minimum surface area is 173.55 ft²
Step-by-step explanation:
Surface area is given by:
\(S(x) = x^2+\frac{880}{x}\)
The value of x for which the derivate of the surface area function is zero, is the length of the sides of the base that minimizes surface area:
\(S(x) = x^2+\frac{880}{x} \\\frac{dS(x)}{dx}=0=2x-\frac{880}{x^2}\\x^3=440\\x=7.606\ ft\)
The height of the box is given by:
\(V=hx^2\\220 =h*7.606^2\\h=3.802\ ft\)
The dimensions of the box with minimum surface area are:
Length of the sides of the base (x) = 7.606 ft
Height (h) = 3.802 ft
The absolute minimum is:
\(S(x) = 7.606^2+\frac{880}{7.606}\\S_{min}=173.55\ ft^2\)
The minimum surface area is 173.55 ft²
Answer:
The absolute minimum of the surface area\(=173.55$ ft^2\)
At the minimum surface area,
Base length=7.61 feetHeight of 3.8 feet.Step-by-step explanation:
Volume of the box =220 cubic feet.
\(\text{Surface Area, } S(x)=x^2+\dfrac{880}{x}\)
To find the absolute minimum of the surface area function on the interval \((0,\infty)\), we take the derivative of S(x) and solve for its critical points.
\(S(x)=\dfrac{x^3+880}{x}\\S'(x)=\dfrac{2x^3-880}{x^2}\\$Setting the derivative equal to 0\\S'(x)=\dfrac{2x^3-880}{x^2}=0\\2x^3-880=0\\2x^3=880\\$Divide both sides by 2\\x^3=440\)
Take the cube root of both sides
\(x=\sqrt[3]{440}\\ x=7.61$ ft\)
Therefore, the absolute minimum of the surface area function on the interval \((0,\infty)\), is:
\(S(x)=\dfrac{7.61^3+880}{7.61}\\\\=173.55$ ft^2\)
Since the volume of the box =220 cubic feet
\(V=x^2h\\220=7.61^2 \times h\\h=220 \div 7.61^2\\h=3.80 ft\)
The dimensions of the box with the minimum surface area are base length of 7.61 feet and height of 3.8 feet.
a farmer has two types of milk, one that is 28% butterfat and another that is 16% butterfat. how many gallons of each should be combined to create a 60-gallon mixture that is 22.5% butterfat?
Answers
30 gallons of 28% butterfat and 30 gallons of 16% butterfat should be combined to create a 60-gallon mixture that is 22 % butterfat.
Let x gallon of 28% butterfat mixed with the y gallon of 16% butterfat to obtain 60 gallons of 22.5% butterfat,
⇒ x + y = 60 ⇒ x = 60 - y ----(1),
Quantity of butterfat in x gallon + quantity of butterfat in y gallon = total quantity of butterfat,
⇒ 28% of x + 16% of y = 22% of 60
⇒ 0.28x + 0.16y = 0.22 × 60
⇒ 0.28x + 0.16y = 13.2
⇒ 28x + 16y = 1320
⇒ 14x + 8y = 660
From equation (1),
14(60-y) + 8y = 660
840 - 14y + 8y = 660
6y = 180
y = 30
Again from equation (1),
x = 60 - y
= 60 - 30
= 30
Hence, 30 gallons of 28% butterfat and 30 gallons of 16% butterfat are combined to create a 60-gallon mixture that is 22%
To learn more about percentages;
https://brainly.com/question/28773949
#SPJ1
Write a polynomial equation with integer coefficients that has the given roots.
x = -8, x = 7
Answers
Answer:
x²+x-56
Step-by-step explanation:
If x=-8 and x=7 are the roots then x+8 and x-7 are the factors. Find the product of the factors to obtain the polynomial.
(x+8)(x-7)
x²-7x+8x-56
x²+x-56
Similarly,we could use Vieta's formula
x²-(sum of roots)x+(product of roots)
x²-(-8+7)x+(-8×7)
x²-(-1)x+(-56)
x²+x-56
Which expression is equivalent to (2g^5)^3
Answers
Pls mark me brainliest
Answer:
Your answer should be 8g^15
Step-by-step explanation:
If cubed (power of 3) is on a parenthesis, that means you have to cube every expression inside that parenthesis. In order to distribute exponents, mutliply them. This gives you g^5 times ^3, which is g^15. ^3 has to also be distributed to the 2, which is 2^3 = 8. 8 and g^15 is 8g^15.
4x2 + 14 - 9x
X = 52

Answers
Answer:
69
Step-by-step explanation:
just plug in 5 for all the x in the equation and mulitply
Answer:
jejeiriiririrurur7urur
Please help me with this problem thank you!

Answers
Answer:
the awnser is or I'm 4th grade
PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP
Answers
Answer:
42 cm²
Step-by-step explanation:
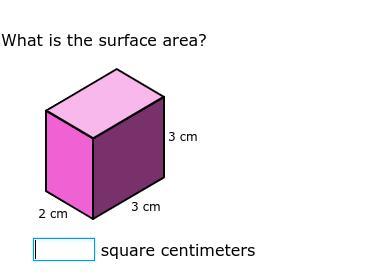
let :
length (l) = 3cm
breadth (b) = 2cm
height (h) = 3cm
formula to find the total surface area is:
2(l×b) + 2(l×h) + 2(b×h)
= 2(3×2) + 2(3×3) + 2(2×3)
= 2×6 + 2×9 + 2×6
= 12 + 18 + 12
= 42
in the figure we needed to find the area and the unit is in cm that's why the unit will be "cm²".
hence, the total surface area is 42cm².
Answer: 42
Step-by-step explanation:
3 x 2 = 6 x 2 = 12
3 x 3 = 9 x 2 = 18
3 x 2 = 6 x 2 = 12
12
+
18
+
12
= 42