the annual rainfall in a certain region is approximately normally distributed with mean 42.6 inches and standard deviation 6 inches. round answers to the nearest tenth of a percent. a) what percentage of years will have an annual rainfall of less than 44 inches? 75.9 incorrect% b) what percentage of years will have an annual rainfall of more than 39 inches? 97.1 incorrect% c) what percentage of years will have an annual rainfall of between 38 inches and 43 inches? 34.1 incorrect%
Answers
The percentage of years will have an annual rainfall of less than 44 inches 67%
A certain region is approximately normally distributed with mean 42.6 inches and standard deviation 6 inches.
a.) p(X < x).
Use Excel's norm.dist() function to calculate this probability directory or
convert x to a Z-score and use Excel's norm.s.dist() function or a Z table to find p(Z < z) or
convert x to a Z-score and look up the Z-score in a Z-table
norm.dist(x, mean, sd, True)
norm.dist(44, 41.6, 5.4, True). the 'True' tells excel to work with the cumulative normal distribution.
or
Z = (44 - 41.6)/5.4 = .44
p(Z <= .44) = .67 or 67%
b.) p(X > x). Use the above mentioned tools to calculated the p(X <= x) then calculate 1- p(X <= x). This will give you p(X > x)
c.) This is the "find the interval" part of the problem. Find p(X <= x_1), p(X <= x_2), then subtract the smaller from the larger probability. This will give you the probability of x's being in the interval state.
p(37 <= x <= 42) = p(X <= 42) - p(X <= 37)
Note: in a continuous distribution such as the normal distribution, we may assume continuity, so p(x > x) = p(x >= x), p(x < x) = p(x <= x)
Therefore, the percentage of years will have an annual rainfall of less than 44 inches 67%
To learn more about normal distribution refer here
https://brainly.com/question/4079902
#SPJ4
Related Questions
i need help #3 pleasee

Answers
x=4
subtract 8 instead of 2
the sum of ages of two brothers A and B is 35 A is two thirds of B's age find their ages
Answers
Answer:
let the ages of the brothers be 2x and 3x
2x +3x=35
5x=35
x=35÷5
x=7
now,
A=2x=2×7=14
B=3x=3×7=21
this is the answer
You want to wrap a gift shaped like the regular triangular prism shown. How many square inches of wrapping paper do you need to completely cover the prism?
Answers
The resulting expression represents the total surface area of the triangular prism. To determine the number of square inches of wrapping paper needed, you would measure the values of 'b', 'h', and 'H' in inches and plug them into the formula.
To determine the amount of wrapping paper needed to cover a regular triangular prism, we need to find the total surface area of the prism.
A regular triangular prism has two congruent triangular bases and three rectangular faces. The formula for the surface area of a regular triangular prism is:
Surface Area = 2(base area) + (lateral area)
To calculate the base area, we need to know the length of the base and the height of the triangle. Let's assume the length of the base is 'b' and the height of the triangle is 'h'. The base area can be calculated using the formula:
Base Area = (1/2) * b * h
Next, we need to calculate the lateral area. The lateral area is the sum of the areas of all three rectangular faces. Each rectangular face has a width equal to the base length 'b' and a height equal to the height of the prism 'H'. Therefore, the lateral area can be calculated as:
Lateral Area = 3 * b * H
Finally, we can substitute the values of the base area and lateral area into the surface area formula:
Surface Area = 2 * Base Area + Lateral Area
= 2 * [(1/2) * b * h] + 3 * b * H
= b * h + 3 * b * H
for more question on prism
https://brainly.com/question/23963432
#SPJ8
select the correct answer. which expression is equivalent to this polynomial? 9x2 4 a. (3x 2i)(3x − 2i) b. (3x 2)(3x − 2) c. (3x 2i)2 d. (3x 2)2
Answers
The polynomial 9x^2 + 4 is equivalent to (3x+2i)(3x-2i). The answer is A.
Polynomials are algebraic expressions that consist of variables and coefficients where arithmetic operations can be performed.
A polynomial is expanded if no variable appears within parentheses and all like terms have been combined.
To expand a polynomial, multiply its factors (often by using the distributive property) or perform the indicated operations. Then combine all like terms.
Expanding each of the options provided using FOIL method:
a) (3x+2i)(3x-2i)
= 9x^2 - 2ix + 2ix - 4i^2
= 9x^2 - 4i^2 *(i^2 = -1) note that i is an imaginary number and i squared is equal to -1
= 9x^2 - 4(-1)
= 9x^2 + 4
b) (3x+2)(3x-2)
= 9x^2 + 6x - 6x - 4
= 9x^2 - 4
c) (3x + 2i)^2
= 9x^2 + 6ix + 6ix + 4i^2 *(i^2 = -1)
= 9x^2 + 12ix - 4
d) (3x + 2)^2
= 9x^2 + 6x + 6x + 4
= 9x^2 + 12x + 4
Hence, the polynomial 9x^2 + 4 is equivalent to (3x+2i)(3x-2i). The answer is A.
To learn more about polynomials: https://brainly.com/question/1218464
#SPJ4
The first step to use to solve for the missing side?

Answers
Answer:
9√2.
Step-by-step explanation:
Distance of the diagonal
= √(9^2 + 9^2 ) (Using Pythagoras Theorem)
= √(162)
= 9√2
Ranjit has six coins in his pocket.
If he picks five of the coins the most he could pick is £4.60 the least he could pick is £2.70
How much money does he have altogether?
Answers
Answer:
Ranjit has £6.50 altogether
Step-by-step explanation:
To find out how much money Ranjit has altogether, we need to use algebraic equations. Let's assume that the value of the first coin is x, the second coin is y, the third coin is z, the fourth coin is a, the fifth coin is b and the sixth coin is c. Therefore, we can write:
x + y + z + a + b = £4.60 --- Equation 1
x + y + z + a + c = £2.70 --- Equation 2
To solve for the values of x, y, z, a, b and c, we need to use simultaneous equations. Subtracting Equation 2 from Equation 1, we get:
b - c = £1.90 --- Equation 3
Since we know that the value of each coin must be positive, we can assume that b > c. Therefore, we can rewrite Equation 3 as:
b = c + £1.90
Substituting this into Equation 1, we get:
x + y + z + a + (c + £1.90) = £4.60
x + y + z + a + c = £2.70
Subtracting these two equations, we get:
£1.90 = b - c = (c + £1.90) - c = £1.90
This means that b = £3.80 and c = £1.90.
Substituting these values back into Equations 1 and 2, we get:
x + y + z + a = £0.90 --- Equation 4
x + y + z + a = £0.80 --- Equation 5
Since Equations 4 and 5 are identical, this means that there are infinitely many solutions for x, y, z and a that satisfy the given conditions. Therefore, we cannot determine the exact amount of money that Ranjit has altogether.
However, we do know that the sum of all six coins must be equal to the sum of the five coins that Ranjit picked plus the value of the coin that he didn't pick. Therefore, we can write:
x + y + z + a + b + c = (sum of all six coins)
= (sum of five coins) + (value of sixth coin not picked)
= £4.60 + £1.90
= £6.50
Therefore, Ranjit has £6.50 altogether.
If f'(c) < 0 then f(x) is decreasing and the graph of f(x) is concave down when x = c. True False Question 4 (1 point). A local extreme point of a polynomial function f(x) can only occur when f'(x) = 0. True False Question 5 (1 point) If f'(x) > 0 when x < c and f'(x) < 0 when x > c, then f(x) has a maximum value when x = C. True False
Answers
Question 3: True
Question 4: False
Question 5: True
If the derivative of a function, f'(x), is positive for values of x less than c and negative for values of x greater than c, then it indicates a change in the slope of the function. This change from positive slope to negative slope suggests that the function has a maximum value at x = c.
This is because the function is increasing before x = c and decreasing after x = c, indicating a peak or maximum at x = c.
Question 3: If f'(c) < 0 then f(x) is decreasing and the graph of f(x) is concave down when x = c.
True
When the derivative of a function, f'(x), is negative at a point c, it indicates that the function is decreasing at that point. Additionally, if the second derivative, f''(x), exists and is negative at x = c, it implies that the graph of f(x) is concave down at that point.
Question 4: A local extreme point of a polynomial function f(x) can only occur when f'(x) = 0.
False
A local extreme point of a polynomial function can occur when f'(x) = 0, but it is not the only condition. A local extreme point can also occur when f'(x) does not exist (such as at a sharp corner or cusp) or when f'(x) is undefined. Therefore, f'(x) being equal to zero is not the sole requirement for a local extreme point to exist.
Question 5: If f'(x) > 0 when x < c and f'(x) < 0 when x > c, then f(x) has a maximum value when x = c.
True
If the derivative of a function, f'(x), is positive for values of x less than c and negative for values of x greater than c, then it indicates a change in the slope of the function. This change from positive slope to negative slope suggests that the function has a maximum value at x = c. This is because the function is increasing before x = c and decreasing after x = c, indicating a peak or maximum at x = c.
Learn more about Polynomial Function at
brainly.com/question/11298461
#SPJ4
Apply green’s theorem to evaluate the integral ∮ ( 2 2) where c is the triangle bounded by x = 0, x y = 1, and y = 0
Answers
The value of the line integral ∮ (2, 2) around the triangle bounded by x = 0, xy = 1, and y = 0 is 0.
To apply Green's theorem, we need to calculate the line integral of the vector field F = (2, 2) around the triangle bounded by the curves x = 0, xy = 1, and y = 0.
Let's start by finding the bounds of integration for the line integral. The triangle is defined by three sides:
1. The segment from (0, 0) to (1, 0) along the x-axis.
2. The segment from (1, 0) to (0, 1).
3. The segment from (0, 1) to (0, 0) along the y-axis.
We can break down the line integral into three separate line integrals along each of these sides and then sum them up.
1. Line integral along the segment from (0, 0) to (1, 0):
We parametrize this line segment as r(t) = (t, 0), where t ranges from 0 to 1.
The differential element of arc length ds is given by ds = sqrt(dx^2 + dy^2) = dt.
Thus, the line integral along this segment becomes:
∮ (2, 2) ⋅ ds = ∫[0,1] (2, 2) ⋅ (dt, 0) = ∫[0,1] 2 dt = 2∫[0,1] dt = 2[t] from 0 to 1 = 2.
2. Line integral along the segment from (1, 0) to (0, 1):
We parametrize this line segment as r(t) = (1 - t, t), where t ranges from 0 to 1.
The differential element of arc length ds is given by
ds = \(\sqrt{(dx^2 + dy^2) }\)
= (\(\sqrt{(-dt)^2 + dt^2)}\)
= \(\sqrt{2}\) dt.
Thus, the line integral along this segment becomes:
∮ (2, 2) ⋅ ds = ∫[0,1] (2, 2) ⋅ (-dt, dt) = ∫[0,1] 0 dt = 0.
3. Line integral along the segment from (0, 1) to (0, 0):
We parametrize this line segment as r(t) = (0, 1 - t), where t ranges from 0 to 1.
The differential element of arc length ds is given by ds = sqrt(dx^2 + dy^2) = dt.
Thus, the line integral along this segment becomes:
∮ (2, 2) ⋅ ds = ∫[0,1] (2, 2) ⋅ (0, -dt) = ∫[0,1] -2 dt = -2[t] from 0 to 1 = -2.
Summing up the line integrals from all three segments:
∮ (2, 2) ⋅ ds = 2 + 0 - 2 = 0.
Learn more about integrals here:
https://brainly.com/question/32770305
#SPJ11
what is the answer for this question
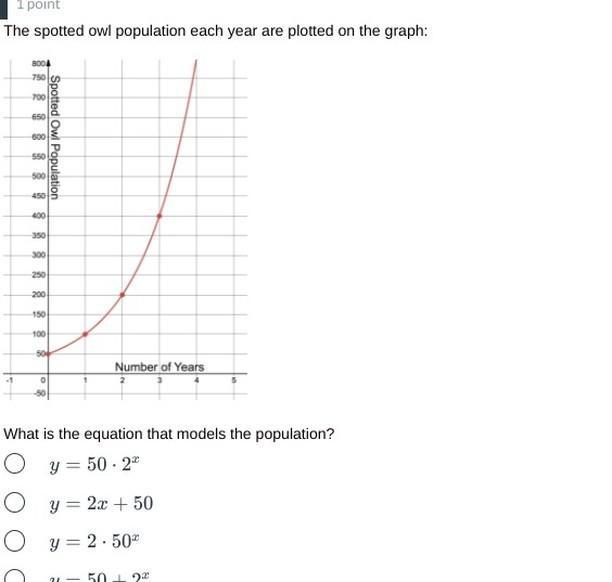
Answers
Derek buys a house for £150,000
He sells the house for £154,500
Work out Derek's percentage profit.
Answers
Answer:
cost price=$150,000
selling price =$154,000
profit= $154,000-$150,000=$4,000
Therfore Percentage Profit= 4,000÷15,000×100=2.7%
Percentage Profit =2.7%
A hotel charges a $3.50 fee for each telephone call
made with an additional charge of $0.10 per minute or
part thereof that the call lasts. Which of the following
expressions represents the cost, in dollars, of making a
phone call that lasts m minutes?
A Bm
(B3510m
(3.5 mm
(D) 45m
(D) 1.6m
Answers
Calculate the perimeter of of the shape below. Show you work

Answers
Answer:
22 is the perimeter.
Step-by-step explanation:
You find the perimeter by adding up all of the sides of a shape. 9 + 9 = 18. 18 + 4 = 22.
Ted works as a travel guide for a mountain resort, earning
$15.72 per hour. Ted is paid weekly, and works 40 hours in
one week. His current federal withholding per week is $69.
He works in a state with a flat-rate income tax of 4.63%. He
will receive a raise of 5% of his hourly rate. Determine the
change in Ted's net pay per paycheck, after taxes, if his new
federal withholding per week is $75.
Answers
Ted's net pay per week after the taxes is $559.09
Net Pay:
Net pay means take-home pay or the amount employees earn after all payroll deductions are subtracted from their gross pay.
Given,
Ted works as a travel guide for a mountain resort, earning $15.72 per hour. Ted is paid weekly, and works 40 hours in one week. His current federal withholding per week is $69. He works in a state with a flat-rate income tax of 4.63%. He will receive a raise of 5% of his hourly rate.
Here we need to find the Ted's net pay per paycheck, after taxes, if his new federal withholding per week is $75.
Through the given details we know that,
Per hour pay = $15.72
Total work per week = 40
So, the total amount for a week is
=> 15.72 x 40
=> $628.8
After federal withholding tax, then the amount is
=> $628.8 - 69
=> $559.8
Now the tax is 4.63%, then
=> $559.8 x 4.63%
=> $559.8 x (4.63/100)
=> $25.91
So, the remaining amount is
=> $559.8 - $25.91
=> $533.88
Now, he will receive 5% for his hourly rate,
Then,
=> $15.72 x (5%)
=> $15.72 x (5/100)
=> 0.78
So, the increased amount is
=> $16.5
Now, the net pay is,
=> (16.5 * 40) - (75 + 25.91)
=> 660 - 100.91
=> 599.09
So, Ted's net pay per paycheck, after taxes is $559.09.
To know more about Net Pay here.
https://brainly.com/question/14690804
#SPJ1
Help please I WILL MARK BRAINLIEST

Answers
Answer:
SAS
Step-by-step explanation:
DB and BD are equal
The angles near D are equal
AD and DC are equal
Side Angle Side
Jennifer is taking a quiz and has answered 13 questions so far. if there are 25 questions on Jennifer's test, how many questions does she have left to answer?
Answers
Answer:
12 questions left.
Step-by-step explanation:
9 = 3d + 3 what is d
Answers
Answer:
2
Step-by-step explanation:
\(9 = 3d + 3 \\ 9 - 3 = 3d \\ 6 = 3d \\ \frac{6}{3} = d \\ 2 = d \\ \huge \purple{ \boxed{ d = 2}}\)
Answer:
9 = 3d + 3
-3 -3
=6 =0
3d=6
To get D we divide since 3 is being times by a number (d which is unknown)
6/3 = 2
2 is the answer.
Step-by-step explanation:
What is the value of y in the equation y = 3x - 2. whenx = 2? *
Answers
Answer:
4
Step-by-step explanation:
y=3x-2
y=3(2)-2
y=6-2
y=4
y=4
Explanation:
x=2
3x = 3 times by x = 2x3
2x3=6
6-2=4
Therefore y = 4
5. a bag of chocolates is labeled to contain 0.384 pounds of chocolates. the actual weight of the chocolates is 0.3798 pounds. a. are the chocolates heavier or lighter than the weight stated on the label? explain how you know. b. how much heavier or lighter are the chocolates than stated on the label? show your
Answers
Comparing the values by subtraction, the chocolates are lighter than the weight stated on the label by 0.0042 pounds.
When comparing two values whether which is greater, compare the digits from left to right.
Comparing 0.384 to 0.3798, where the first digits are both 0, and the digit after the decimal are also the same, compare the hundredth's place.
8 > 7
Hence, the actual weight of the chocolates is less than or lighter than the weight stated on the label.
Using subtraction, two values can also be compared by getting how much one exceeds the other.
Subtracting the two values,
0.384 - 0.3798 = 0.0042 pounds
Learn more about comparing values by subtraction here: brainly.com/question/66864
#SPJ4
Discuss the existence and uniqueness of a solution to the differential equation 3+ 2)y"y-y-tant that satisfies the initial conditions y(3)- Yo.y(8)-Y, where Yo and Y1 are real constants. Select the correct choice below and fill in any answer boxes to complete your choice A. A solution is guaranteed on the interval___< t < because its contains the point T0 =___ and the function p(t)= ___ q(t)___ and gt ___ are equal on the interval B. A solution is guaranteed on the interval___< t < because its contains the point T0 =___ and the function p(t)= ___ q(t)___ and gt ___ are simultaneously countionous on the interval C. A solution is guaranteed only at the pouint T0 =___ and the function p(t)= ___ q(t)___ and gt ___ are simultaneously defined at the point
Answers
The solution to the differential equation that satisfies the initial conditions y(3) = y0 and y(8) = y1 is:
y(t) = (2/3)t - (1/3)cos(t) + (1/3)sin(t) + y1 + (1/3)sin(3) - (2
The given differential equation is:
3y''+2y'y-y-tan(t)=0
To check the existence and uniqueness of a solution, we need to verify if the function p(t) and q(t) satisfy the conditions of the Existence and Uniqueness Theorem.
The Existence and Uniqueness Theorem states that if the functions p(t) and q(t) are continuous on an interval containing a point t0 and if p(t) is not equal to zero at t0, then there exists a unique solution to the differential equation y'' + p(t) y' + q(t) y = g(t) that satisfies the initial conditions y(t0) = y0 and y'(t0) = y1.
Comparing the given differential equation with the standard form of the Existence and Uniqueness Theorem, we get:
p(t) = 2y(t)
q(t) = -t - tan(t)
g(t) = 0
To find the interval of existence, we need to check the continuity of p(t) and q(t) and also the value of p(t) at t0.
Here, p(t) is continuous everywhere and q(t) is continuous on the interval (3, 8). To check the value of p(t) at t0, we need to find y(t) that satisfies the initial conditions y(3) = y0 and y(8) = y1.
Let's assume that y(t) = A(t) + B(t), where A(t) satisfies y(3) = y0 and A'(3) = 0 and B(t) satisfies y(8) = y1 and B'(8) = 0.
Solving the differential equation for A(t), we get:
A(t) = c1 cos(sqrt(3)(t-3)) + c2 sin(sqrt(3)(t-3)) + (2/3)t - (1/3)cos(t) + (1/3)sin(t) + (1/3)sin(3)
Using the initial conditions y(3) = y0 and A'(3) = 0, we get:
A(t) = (2/3)t - (1/3)cos(t) + (1/3)sin(t) + (1/3)sin(3) - (2/3)cos(3) - y0
Solving the differential equation for B(t), we get:
B(t) = c3 cos(sqrt(3)(t-8)) + c4 sin(sqrt(3)(t-8)) + (2/3)t - (1/3)cos(t) + (1/3)sin(t) - (1/3)sin(3)
Using the initial conditions y(8) = y1 and B'(8) = 0, we get:
B(t) = (2/3)t - (1/3)cos(t) + (1/3)sin(t) - (1/3)sin(3) + (2/3)cos(3) + y1
Therefore, the solution to the differential equation that satisfies the initial conditions y(3) = y0 and y(8) = y1 is:
y(t) = (2/3)t - (1/3)cos(t) + (1/3)sin(t) + y1 + (1/3)sin(3) - (2)
For more questions like Differential equation click the link below:
https://brainly.com/question/14598404
#SPJ11
A dilation has center (0,0). Find the image of the point L(6-8) for the scale factor 7.

Answers
Answer:
D (42,-56)
Step-by-step explanation:
Scale factor means you multiply, so you multiply (6,-8) by 7.
6 x 7 is 42 and 7 x -8 is -56. So your answer is D (42,-56).
Parallelogram MNOP with vertices M(1, 7),
N(8, 5), O(4, 2), and P(-3, 4): and it rotates 180° What will be the new coordinates
Answers
The new coordinates are M'(-1, -7), N'(-8, -5), O'(-4, -2), and P'(3, -4)
What is a 180 degrees rotation?A 180 degrees rotation denoted by R(180, 0) is a rotation that has the same effect as the 180 degrees counterclockwise of a figure.
And it has the algebraic rule of its rotation to be changed from (x, y) to (-x, -y) i.e (x, y) ⇒ (-x, -y)
How to determine the image of the rotation?The coordinates of the parallelogram are given as
M(1, 7), N(8, 5), O(4, 2), and P(-3, 4)
The rotation is given as 180° rotation
As mentioned above,
We have (x, y) ⇒ (-x, -y)
Substitute M(1, 7), N(8, 5), O(4, 2), and P(-3, 4) in (x, y) ⇒ (-x, -y)
So, we have
M'(-1, -7), N'(-8, -5), O'(-4, -2), and P'(3, -4)
Hence, the coordinates of the image are M'(-1, -7), N'(-8, -5), O'(-4, -2), and P'(3, -4)
Read more about rotation at
https://brainly.com/question/12508456
#SPJ1
A sprinkler that sprays water in a circular area can spray up to a radius of 22ft what is the maximum area of lawn that can be watered by the sprinkler use 3.14 to approximate date for Pie enter your answer as a decimal rounded to the nearest tenth in the Box
[ ] ft^2
Answers
To find the maximum area of the lawn that can be watered by the sprinkler, we can use the formula for the area of a circle:
A = πr^2
Given that the radius of the sprinkler's spray is 22ft, we can substitute this value into the formula:
A = 3.14 * (22)^2
A ≈ 3.14 * 484
A ≈ 1519.76
Rounded to the nearest tenth, the maximum area of the lawn that can be watered by the sprinkler is approximately 1519.8 ft^2.\(\huge{\mathcal{\colorbox{black}{\textcolor{lime}{\textsf{I hope this helps !}}}}}\)
♥️ \(\large{\textcolor{red}{\underline{\texttt{SUMIT ROY (:}}}}\)
simplify 4+5(3x - 2) - 3x
Answers
Answer:
12x - 6
Step-by-step explanation:
\( \rm \: 4 + 5(3x - 2) - 3x\)
\( \rm \: = 4 + 15x - 10 - 3x \: \sf (distribute \: the \: 5)\)
\( \rm= 12x - 6 \: \sf (combine \: like \: terms)\)
\( \rm= 6(2x - 1) \: \sf (factor \: out \: a \: 6)\)
\( \rm \: = 6(2x) - 6(1) \: \sf (distribute \: the \: 6)\)
\( \rm \:= 12x - 6 \: \sf (simplify)\)
is the following a probability model? what do we call the outcome "red"?
Answers
The following a probability model? what do we call the outcome No, the provided information is not sufficient to determine if it is a probability model. The outcome "red" is typically referred to as an event.
A probability model is a mathematical representation of a random experiment, where the sample space is defined, and probabilities are assigned to all possible outcomes. To determine if the given information is a probability model, we would need to know the complete list of possible outcomes, their corresponding probabilities, and ensure that the probabilities meet the necessary conditions (sum up to 1 and are non-negative).
Based on the limited information provided, we cannot determine if it is a probability model. The outcome "red" is called an event in the context of probability.
To know more about probability, visit:
https://brainly.com/question/30034780
#SPJ11
one segment measures 161 cm. Calculate its multiple according to the number 3 and its submultiple according to the number 7
Answers
By using multiplication and division, it can be calculated that-
The multiple according to the number 3 = 162
The submultiple according to the number 7 = 7
What is multiplication and division?
Repeated addition is called multiplication. Multiplication is used to find the product of two or more numbers.
Division is the process in which a value of single unit can be calculated from the value of multiple unit.
The number to be divided is called dividend. The number by which dividend is divided is the divisor. The result obtained is called quotient and the remaining part is the remainder.
This is a problem of multiplication and division.
One segment measures 161 cm
So, to find the multiple according to the number 3, we have to divide 161 by 3
161 \(\div\) 3 = 53.67
Nearest integer of 53.67 is 54
The multiple according to the number 3 = 54 \(\times\) 3 = 162
To find the submultiple according to the number 7, we have to divide 161 by 7
161 \(\div\) 7 = 23
Nearest integer of 23 is 23
The submultiple according to the number 7 = 161 \(\div\) 23 = 7
To learn more about multiplication and division, refer to the link-
https://brainly.com/question/28337146
#SPJ1
Using the right triangle below. What is the name for side AB?
A) Hypotenuse
B) Adjacent
C) Opposite
D) None of the above

Answers
Answer:
A.Hypotenuse
Step-by-step explanation:
Side AB is the longest side of the triangle
The longest side of a triangle is known as the hypotenuse
Anthony shines a beam of light on the surface of a solution of glycerol at a certain angle. if the angle of refraction is 38°, what is the angle of incidence? the index of refraction of glycerol is 1.47, while that of air is 1.00. a. 38° b. 45° c. 55° d. 65° e. 70°
Answers
Answer:
D) 65°
Step-by-step explanation:
Use Snell's Law
\(n_1\sin\theta_1=n_2\sin\theta_2\\\\1.00\sin\theta_1=1.47\sin38^\circ\\\\\sin\theta_1=1.47\sin38^\circ\\\\\theta_1=\sin^{-1}(1.47\sin38^\circ)\\\\\theta_1\approx64.83^\circ\)
Thus, the angle of incidence is D) 65°
Employees at a large company can earn monthly bonuses. The distribution of monthly bonuses earned by all employees last year has mean 2.3 and standard deviation 1.3. Let z represent the standard normal distribution. If x represents the mean number of monthly bonuses earned last year for a random sample of 40 employees, which of the following calculations will give the approximate probability that x is less than 2 ?
a. P [ z < (2-2.3 / (1.3/√40)) ]
b. P (z < 2)
c. P [z < (2.3-2 / 1.3) ]
d. P [z < (2-2.3 / 1.3) ]
e. P [z < (2.3 -2 / (1.3/√40)) ]
Answers
The correct calculation to find the probability that x is less than 2 is:
d. P [z < (2 - 2.3 / (1.3/√40))]
We know that the distribution of monthly bonuses earned by all employees last year has mean 2.3 and standard deviation 1.3.
Since we have a sample of size 40, we can use the central limit theorem to approximate the distribution of the sample mean x with a normal distribution with mean 2.3 and standard deviation 1.3/√40.
To find the probability that x is less than 2, we need to find the z-score corresponding to x = 2, given the distribution of x. We can do this using the formula:
z = (x - μ) / σ
where μ is the mean of the distribution of x (which is 2.3) and σ is the standard deviation of the distribution of x (which is 1.3/√40).
Plugging in the values, we get:
z = (2 - 2.3) / (1.3/√40)
z = -1.63
So, the probability that x is less than 2 is equal to the probability that z is less than -1.63, which is given by the standard normal distribution table as:
P [z < -1.63]
Therefore, the correct calculation to find the probability that x is less than 2 is:
d. P [z < (2 - 2.3 / (1.3/√40))]
Learn more about the probability visit:
https://brainly.com/question/13604758
#SPJ12
Three straight lines intersect at $O$, and ray $\overrightarrow{OD}$ divides $\angle COE$ into two angles of equal measure. The ratio of $\angle COB$ to $\angle BOF$ is $7:2$. What is the number of degrees in $\angle COD$?
Answers
Answer:
12
Step-by-step explanation:
m xxq
The required measure of an angle is ∠COD = 40°.
What are the vertical angles?When two lines intersect at a location, vertical angles are generated. They are always equal to each other.
Let's call the measure of \($\angle COE$\) x degrees.
Since \($\overrightarrow{OD}$\) divides \($\angle COE$\) into two angles of equal measure, the measure of each of those angles is \($\frac{x}{2}$\) degrees.
Since the measure of \($\angle COB$\) is 7 times the measure of \($\angle BOF$\), we have \($\angle COB = 7\angle BOF$\). The sum of the measures of the angles of a triangle is \($180^\circ$\), so we can set up the equation \($\angle COB + \angle COE + \angle BOF = 180^\circ$\). Substituting \($7\angle BOF$\) for \($\angle COB$\), we have:
\($7\angle BOF + x + \angle BOF = 180^\circ$\)
Solving for \($\angle BOF$\), we find that \($\angle BOF = 20^\circ$\).
The measure of \($\angle COD$\) is equal to the measure of\($\angle COE$\) minus the measure of \($\angle COD$\), so \($\angle COD = x - 2\cdot 20^\circ = x - 40^\circ$\).
Since the measure of \($\angle COE$\) is equal to \($2\angle COD$\), we have \($x = 2(x - 40^\circ)$\), which simplifies to \($x = 80^\circ$\).
Therefore, the measure of \($\angle COD$\) is \($80^\circ - 40^\circ = {40^\circ}$\).
Learn more about the Angles here:
brainly.com/question/2125016
#SPJ5
1. Use the following graph to determine the coordinated of the y-intercept.
A. (5,0)
B. (4,0)
C. (0,4)
D. (0,5)
HURRY!!! Please.

Answers
Answer:
I believe it's C. (0.4)
Step-by-step explanation: