\(5 2/3 -10\)
Answers
Convert both numbers into fractions.
52/3 - 10/1
Make sure they both have the same denominator
52/3 - 30/3
Now you can take the numerator and subtract it.
22/3
Now you simply simplify
7 1/3
So the answer is 7 1/3
Related Questions
A jar contains 10 blue marbles, 3 red marbles, and 7 white marbles.
What is the probability of selecting a red marble, then a white marble
without replacement?
Answers
Answer:
50% chance because (10)/(20)=1/2=0.5=50%
Step-by-step explanation:
hope this helps
There are 9 computers and 72 students. What is the unit rate of students to computers? A) 1 computer 8 students B) 8 students 1 computer C) 3 computers 24 students D) 24 students 3 computers
Answers
Answer:
72/9 = 8
Answer is b
8 students to 1 computer
, If two angles add up to 90°, then they are not supplementary
What’s the contrapositive?

Answers
Answer:
supplementary means the angles add upto 180 degrees. The name for 2 anglew which add upto 90 degrees is "complimentary".
Find an equation of the line containing the point (2,-5) and parallel to y = – 4x – 2.
Write your answer in slope-intercept form.

Answers
Answer:
the desired equation is y = – 4x + 3
Step-by-step explanation:
Parallel lines have the same slope and thus similar equations. Thus, the equation of a line parallel to the given line has the form y = – 4x + C. We need only find C.
The new line goes through (2, -5), and so we substitute 2 for x and -5 for y to obtain
-5 = – 4(2) + C. Then -5 + 8 = C, or C = 3.
Then the desired equation is y = – 4x + 3
Length and width of the two cell phones are proportional. What is the worth in inches of the larger version of the cell phone?
Answers
The width of the larger cell phone: \(W_{2}=\frac{(W_{1} *L_{2})}{L_{1} }\)
What is the length?Length is a measure of the size of an object in one dimension. It refers to the distance between two points, usually measured in units such as meters, feet, inches, or centimetres.
What is the width?Width is a measure of the size of an object in one dimension, specifically the distance between its two sides that are parallel to each other. It is usually considered the shorter of the two dimensions, the other being length.
According to the given information:Since the length and width of the two cell phones are proportional, we can express this relationship using a proportion. Let \(L_{1}\) and \(W_{1}\) be the length and width, respectively, of the smaller cell phone, and let \(L_{2}\) and \(W_{2}\) be the length and width, respectively, of the larger cell phone. Then we have:
\(\frac{L_{1} }{W_{1} } =\frac{L_{2} }{W_{2} }\)
We can rearrange this equation to solve for the width of the larger cell phone:
\(W_{2}=\frac{(W_{1} *L_{2})}{L_{1} }\\\)
To know more about the length visit:
https://brainly.com/question/2217700
#SPJ1
What is the average length encoding of a letter for a huffman code of these letters and their frequencies: a : 0.15, b : 0.25, c : 0.20, d : 0.35, e : 0.05?
Answers
The average length encoding of a letter for a Huffman code of the letters and their given frequencies will be 245.
We have,
Frequencies:
a = 0.15 = 15,
b = 0.25 = 25,
c = 0.20 = 20,
d = 0.35 = 35,
e = 0.05 = 5,
So,
Now,
According to the question,
We will make Huffman tree,
i.e.
a = 0.15 = 15,
b + c = 25 + 20 = 45
d + e = 35 + 5 = 40,
Now,
a + b + c + d + e = 100
So,
a = 11 = 2 digits
b = 101 = 3 digits
c= 100 = 3 digits
d= 01 = 2 digits
e= 00 = 2 digits
And,
We know that,
Total bits required to represent Huffman code = 12.
So,
Now,
The average code length = a * 2 digits + b * 3 digits + c * 3 digits + d * 2 digits + e * 2 digits
i.e.
The average code length = 15 × 2 + 25 × 3 + 20 × 3 + 35 × 2 + 5 × 2
On solving we get,
The average code length = 245
Hence we can say that the average length encoding of a letter for a Huffman code of the letters and their given frequencies will be 245.
Learn more about Huffman code here
https://brainly.com/question/18916556
#SPJ4
how many feet of granite was tunneled through to make tunnel no. 6 through the sierra nevada mountains?
Answers
Nearly 1,659 feet of granite was tunnelled through to make tunnel no. 6 through the sierra Nevada mountains.
Early snowfall prevented the Central Pacific from starting construction on Tunnel No. 6, or the Summit Tunnel, in August 1865. It was built using a variety of engineering and construction methods and was located more than seven thousand feet above sea level.
When the workmen finally broke through, they discovered that they were only two inches off from the calculations that were used to locate its end points and central shaft. The length of the tunnel that was built through the Sierra Nevada mountains is therefore given as nearly 1,659 feet of granite was tunnelled through to make tunnel no. 6 through the Sierra Nevada mountains.
Read more about granite on:
https://brainly.com/question/880155
#SPJ4
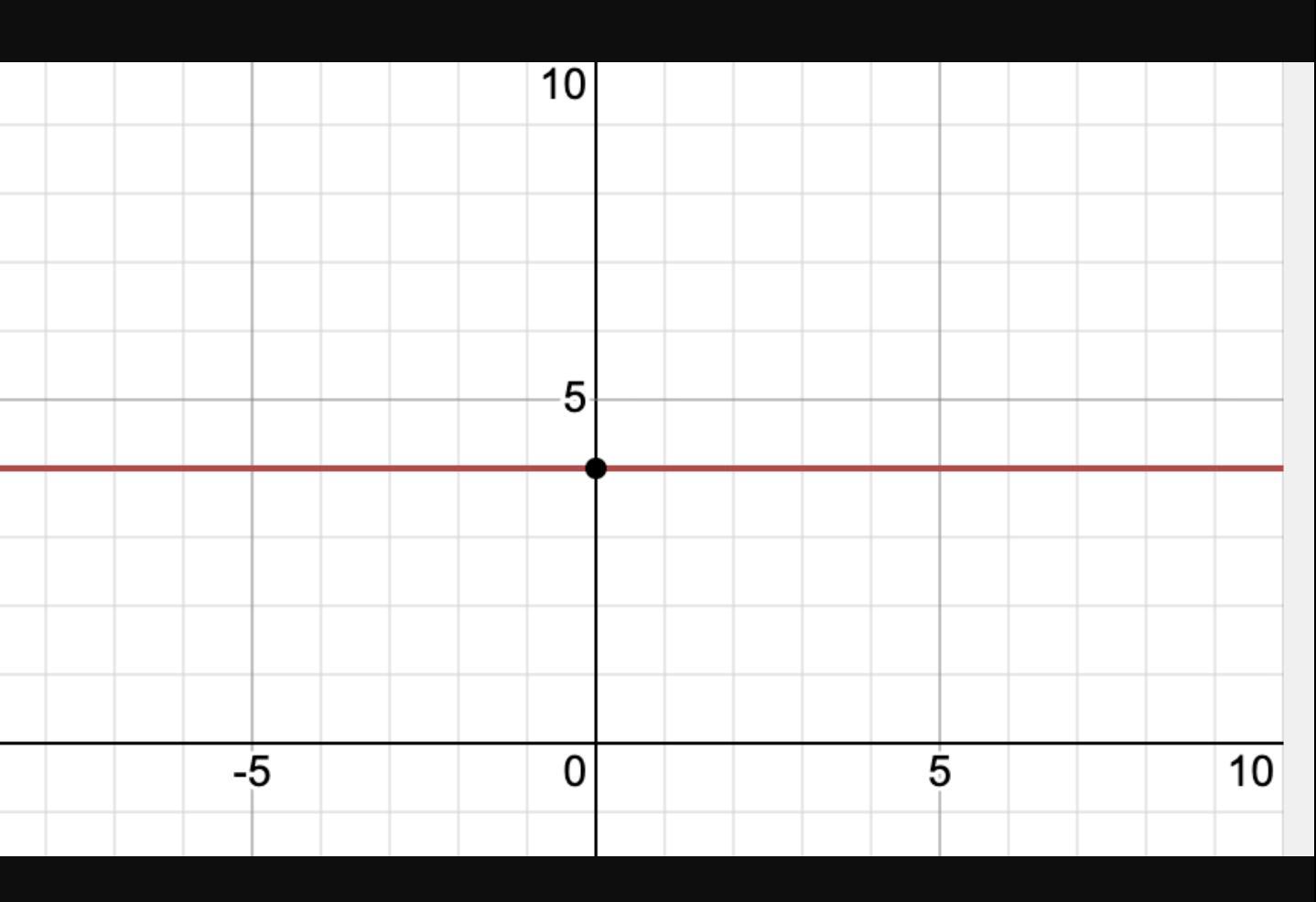
Which graph shows a function where f(2) = 4?
Answers
Answer:the graph should look like this
Step-by-step explanation:
Proportional relationships!!
“A car travels 52 miles per hour.”
You have hours 1,2,5,8 what are the miles used!!
Answers
Step-By-Step Explanation:
1hour = 52×1= 52miles
2hours = 52×2= 104miles
5hours = 52×5= 260miles
8hours = 52×8= 416miles
If this helped, please consider picking this answer as the Brainliest Answer. Thank you!
Suppose you received these grades on your last five quizzes: 16, 17, 18, 19, and 20. If you get 20's on the next three quizzes, which of the following will change? I. Q1 II. Q2 III. Q3 IV. minimum V. maximum
Answers
Answer:
its i, ii, and iii
Step-by-step explanation:
they already had their maximum and minimum so that couldnt change, but getting those 3 20s would make q1, q2, and q3 change. i just took it and got a 100.
Answer:
Hi, have you seen empress
Step-by-step explanation:
Solve the following system of equations algebraically or by graphing.
y=x²-x-6
y=x-3

Answers
The solution to the system of simultaneous equations is; (-1, 4) and (3, 0)
What is the solution to the quadratic equation?We are given two equations as;
y = x² - x - 6 -----(1)
y = x - 3 ----(2)
We will use the algebraic method to solve it as;
The general format for a quadratic equation is;
y = ax² + bx + c
The quadratic formula to solve the quadratic equation is;
x = [-b ± √(b² - 4ac)]/(2a)
Put equation 2 into equation 1 to get;
x - 3 = x² - x - 6
x² - x - x - 6 + 3 = 0
x² - 2x - 3 = 0
Factorizing we have;
x² + x - 3x - 3 = 0
x(x + 1) - 3(x + 1) = 0
Thus;
x - 3 = 0 or x + 1 = 0
x = -1 or 3
Read more about Quadratic Equation Solution at; https://brainly.com/question/1214333
#SPJ1
Jack ran a total of 30 miles over the course of 15 track practices. How many track practices would it take for Jack to run 44 miles? Solve using unit rates.
My brain isn’t functioning and i need this done before December 21.
Answers
Answer:
22
Step-by-step explanation:
Use a proportion.
30/15 = 44/x
30x = 15 × 44
2x = 44
x = 22
Answer:
22
Step-by-step explanation:
30 miles/ 15 sessions of tract practice
Per practice Jack is running a total of 2 miles.
So 44 miles/2 miles
22 sessions of track practice
Given: Circle A externally tangent to Circle B.
How many possible common tangents to circles A and B can exist?
2
3
4

Answers
there are only 2 possible common tangents to circles A and B can exist
ok done. Thank to me :>
Answer:
3
Step-by-step explanation:
Need this ASAP!! Would help if you could answer as quick as possible x

Answers
Answer:
-21p - 7c
Step-by-step explanation:
First you need to multiply the () by -7 or in other words distribute. In order to do this multiply each value in the () by -7
-7(3p) = -21p
-7(c) = -7c
Now rewrite your equation
-21p-7c
There you go!
the ____ format specifier is used to denote a signed decimal integer.
Answers
The "d" format specifier is used to denote a signed decimal integer in various programming languages and formatting systems.
When used in format strings or printf-style functions, the "d" specifier indicates that the corresponding argument should be formatted as a signed decimal integer. It allows for the representation of both positive and negative whole numbers, including zero.
For example, in C programming, the printf function can be used with the "%d" format specifier to display a signed decimal integer value. Similarly, in other languages such as Python, the "{:d}" format specifier can be used with the format() function or string interpolation to represent a signed decimal integer.
Using the "d" specifier ensures that the output is formatted as a base-10 representation of a signed integer, taking into account the sign of the number.
To know more about "d" format specifier refer here:
https://brainly.com/question/10665222#
#SPJ11
Which expression (x^22)(x^7)^3 equivalent to X^p
Answers
Answer:
p = 43
Step-by-step explanation:

FILL IN THE BLANK. the quantitative relation between two amounts showing the number of times one value contains or is contained within the other definition. ___
Answers
Ratio is the relation between two amounts that shows the number of times one value contains within the other.
What is Ratio?
A ratio in mathematics illustrates how many times one number contains another. For example, if a dish of vegetables contains eight tomato and six carrots, the tomato-to-carrot ratio is eight to six (that is, 8:6, which is equivalent to the ratio 4:3). Similarly, the proportion of carrots to tomato is 6:8 (or 3:4), while the proportion of tomato to overall fruit is 8:14. (or 4:7). A ratio's numbers can be any quantity, such as a count of persons or things, or measures of lengths, weights, time, and so forth. In most situations, both numbers must be positive.
Solution:
Ratio is the relation between two amounts that shows the number of times one value contains within the other.
To learn more about Ratio from the given link
https://brainly.com/question/2328454
#SPJ4
How are 1 and 2 related?

Answers
express cos6mcos2m as a sum or difference
Answers
Given :
An expression (cos 6m)(cos 2m) .
To Find :
We need to express it in terms as sum or difference.
Solution :
We know,
cos( A + B ) = cosA cos B - sin A sin B
cos( A - B ) = cosA cos B + sin A sin B
Adding both the equations we get :
2cos A cos B = cos( A + B) + cos( A - B )
or
cos A cos B = cos( A + B) + cos( A - B )/2
Putting value of A = 6m and B = 2m in above equation, we get :
(cos 6m)(cos 2m) = cos( 6m + 2m ) + cos( 6m - 2m )/2
(cos 6m)(cos 2m) = cos(8m) + cos(4m)/2
Hence, this is the required solution.
This is an equation puzzle.
Fill in each blank with a number so that each row and column makes a true equation.

Answers

Consider the PDE au(x, t) = 4 d²u(x, t) 2 Ət əx² For each of BCs and ICs, solve the initial value problem. du(π,t) a) BCs: u(0,t)=0 = = 0 and əx IC: u(x,0) = x ANSWER: f(x)= n=1 u(2,t) = 0 and u(0,t)=0 u(x,0)=sin x ANSWER: f(x)=¹1_sin(2 + nx) na n=1 1+ 2 X b) BCs: IC: 8 (2n-1) T n+1 (-1)041 -4(2n-1)²t sin(2-nπ) nπ 1- 2 e sin (2n-1) 2 na sin X 2 -(nn)²t x -X
Answers
the solution for the initial value problem is: u(x, t) = sin(sqrt(-λ² * (a / 4)) * x) * exp(-λ² * t) where λ = ± sqrt(-4n² / a), and n is a non-zero integer.
The given partial differential equation is:
au(x, t) = 4 * (d²u(x, t) / dt²) / (dx²)
a) BCs (Boundary Conditions):
We have u(0, t) = 0 and u(π, t) = 0.
IC (Initial Condition):
We have u(x, 0) = x.
To solve this initial value problem, we need to find a function f(x) that satisfies the given boundary conditions and initial condition.
The solution for f(x) can be found using the method of separation of variables. Assuming u(x, t) = X(x) * T(t), we can rewrite the equation as:
X(x) * T'(t) = 4 * X''(x) * T(t) / a
Dividing both sides by X(x) * T(t) gives:
T'(t) / T(t) = 4 * X''(x) / (a * X(x))
Since the left side only depends on t and the right side only depends on x, both sides must be equal to a constant value, which we'll call -λ².
T'(t) / T(t) = -λ²
X''(x) / X(x) = -λ² * (a / 4)
Solving the first equation gives T(t) = C1 * exp(-λ² * t), where C1 is a constant.
Solving the second equation gives X(x) = C2 * sin(sqrt(-λ² * (a / 4)) * x) + C3 * cos(sqrt(-λ² * (a / 4)) * x), where C2 and C3 are constants.
Now, applying the boundary conditions:
1) u(0, t) = 0:
Plugging in x = 0 into the solution X(x) gives C3 * cos(0) = 0, which implies C3 = 0.
2) u(π, t) = 0:
Plugging in x = π into the solution X(x) gives C2 * sin(sqrt(-λ² * (a / 4)) * π) = 0. To satisfy this condition, we need the sine term to be zero, which means sqrt(-λ² * (a / 4)) * π = n * π, where n is an integer. Solving for λ, we get λ = ± sqrt(-4n² / a), where n is a non-zero integer.
Now, let's find the expression for u(x, t) using the initial condition:
u(x, 0) = X(x) * T(0) = x
Plugging in t = 0 and X(x) = C2 * sin(sqrt(-λ² * (a / 4)) * x) into the equation above, we get:
C2 * sin(sqrt(-λ² * (a / 4)) * x) * C1 = x
This implies C2 * C1 = 1, so we can choose C1 = 1 and C2 = 1.
Therefore, the solution for the initial value problem is:
u(x, t) = sin(sqrt(-λ² * (a / 4)) * x) * exp(-λ² * t)
where λ = ± sqrt(-4n² / a), and n is a non-zero integer.
Note: Please double-check the provided equation and ensure the values of a and the given boundary conditions are correctly represented in the equation.
To know more about Equation related question visit:
https://brainly.com/question/29657983
#SPJ11
Jada recorded the thickness a of a set of books. This line plot shows her results.
Jada stacked the books that were (1 1/2) inches thick on top of the books that were
(2 1/4) inches thick.
How thick was her pile of books?

Answers
The total thickness of Jada's pile of books was 12 inches.
What is line plot?A graph form used to display numerical data is a line plot, commonly referred to as a dot plot. Each data point in a line plot is represented by a dot that is positioned above a number line. Dots that indicate the same value are piled vertically and put above the appropriate value on the number line.
Little to intermediate sized data sets may be displayed using line plots, which enable us to rapidly observe the data's distribution, including its range, frequency, and any outliers.
Two data points on the line plot indicate a set of books that were each one and a half inches thick, indicating that there were two of such types of books.
Four data points on the line plot indicate a set of books that were each 2 1/4 inches thick, indicating that there were four of such types of books.
Total thickness = (2 x 1 1/2) + (4 x 2 1/4)
= 3 + 9
= 12 inches
Hence, the total thickness of Jada's pile of books was 12 inches.
Learn more about line plot here:
https://brainly.com/question/29573088
#SPJ1
One side of a square is 445mm long. Find the area in cm²
Answers
Answer:
1,980.25cm^2
Step-by-step explanation:
445mm=44.5cm
44.5^2=1,980.25
what is the result of the following boolean expression, if x equals 5, y equals 3, and z equals 8? x < y and z > x
Answers
If x<y and z>x then the solution is true.
What is meant by Boolean operators?Boolean operators are straightforward words (AND, OR, NOT, or AND NOT) that are used as conjunctions in searches to combine or exclude terms, producing more specialized and useful results.
What are Boolean and examples?An expression that may only be evaluated as true or false is called a boolean expression (after mathematician George Boole). Let's examine some examples in everyday language: Pink is one of my favorite colors. I'm apprehensive about programming computers.
From the above theory we can say that
if x=5, y=3 and z=8
and if the conditions are x<y or z>x
Then it is true
as one of them is correct.
To know more about boolean expression click the following link
https://brainly.com/question/25039269
#SPJ1
Drag the tiles to the correct boxes to complete the pairs. not all tiles will be used. simplify the expressions and match them with their solutions. (2 5i)2 − 20i 1 (4 i)(-4 i) ÷ 17 (3 2i)2 − (2 3i)2 2i(5 4i) − 5(3 2i) (-2i)4 (3i)3 (27i) -1 10 -20 16
Answers
(2 + 5i)^2 − 20i = -16 + 20i
(4i)(-4i) ÷ 17 = -16i^2 / 17 = 16/17
(3 + 2i)^2 − (2 + 3i)^2 = -10 + 20i
2i(5 + 4i) − 5(3 + 2i) = -7 - 8i
(-2i)^4 = 16
(3i)^3 = -27i
(27i)^-1 = -i/27
10, -20, 16
For (2 + 5i)^2 − 20i, we square the complex number, which gives 4 + 20i - 25 + 20i. Combining like terms, we get -21 + 40i, which simplifies to -16 + 20i.
For (4i)(-4i) ÷ 17, we multiply -4i with itself, which gives -16i^2. Since i^2 is equal to -1, we have -16(-1) ÷ 17 = 16/17.
For (3 + 2i)^2 − (2 + 3i)^2, we square both complex numbers, resulting in 9 + 12i + 4i^2 − 4 − 12i − 9i^2. Simplifying further, we get -10 + 20i.
For 2i(5 + 4i) − 5(3 + 2i), we perform the multiplication and combine like terms to obtain -7 - 8i.
For (-2i)^4, we raise -2i to the power of 4, which equals 16.
For (3i)^3, we cube 3i, resulting in -27i.
For (27i)^-1, we find the reciprocal of 27i, which is -i/27.
The simplified expressions and their corresponding solutions are:
(2 + 5i)^2 − 20i = -16 + 20i
(4i)(-4i) ÷ 17 = 16/17
(3 + 2i)^2 − (2 + 3i)^2 = -10 + 20i
2i(5 + 4i) − 5(3 + 2i) = -7 - 8i
(-2i)^4 = 16
(3i)^3 = -27i
(27i)^-1 = -i/27
The solutions for the expressions are 10, -20, and 16.
To know more about square , Visit:
https://brainly.com/question/27307830
#SPJ11
How much would you pay for 5 apples at the rate of $6.60 a dozen?
Answers
Answer:
You would pay $2.75
Step-by-step explanation:
a dozen = 12
6.60 / 12 = $0.55
0.55 x 5 = 2.75
Answer:
$2.75 for 5 apples
Step-by-step explanation:
If I understood correctly, you want the answer to 5 apples at the cost of a dozen.
First, you would need to find the cost of a single apple by dividing the price by the dozen. 6.6/5 = 0.55
Next, you multiply the amount of apples by the cost of a single one. 5 * 0.55 = 2.75
And there you go, hope I helped :)
Which construction could be used to construct an isosceles triangle ABC given line segment AB?
A)
Mark a third point C not on segment AB. Draw segments AC and BC.
B)
Label a point C on segment AB and construct a line perpendicular to AB through point C. Draw segments AC and BC.
C)
Construct the perpendicular bisector of segment AB. Mark the intersection of this line and AB and label it C. Draw segments AC and BC.
D)
Construct the perpendicular bisector of segment AB. Mark any point C on the perpendicular bisector except where it intersects AB. Draw segments AC and BC.
Answers
Answer: Choice D
Construct the perpendicular bisector of segment AB. Mark any point C on the perpendicular bisector except where it intersects AB. Draw segments AC and BC.
=======================================================
Explanation:
We start off with segment AB.
Let D be the midpoint, so that AD = DB
The perpendicular line through D is known as the perpendicular bisector. The term "bisect" means to "split in half".
Then we'll place point C anywhere along this new line, as long as it's not at point D's location.
This then helps us form segments AC and BC which are equal in length. This guarantees we have an isosceles triangle since we have 2 sides that are the same length.
Check out the diagram below.

The following curve passes through (3,1). Use the local linearization of the curve to find the approximate value of y at x
Answers
m = the slope of the curve at x=3 and b = the y-intercept at x=3. Therefore, the approximate value of y at x=2
We can use the local linearization of the curve to approximate the value of y at x=2.
The local linearization of the curve is given by the equation y = mx + b, where m is the slope of the curve at x=3 and b is the y-intercept at x=3.
Let m be the slope of the curve at x=3 and b be the y-intercept at x=3.
The slope of the curve at x=3 can be found by calculating the derivative of the curve at x=3.
The y-intercept at x=3 can be calculated by substituting x=3 into the equation of the curve and solving for y.
Therefore, m = the slope of the curve at x=3 and b = the y-intercept at x=3.
Substituting the values of m and b into the equation of the local linearization, we get the equation y = mx + b.
Substituting x=2 into the equation, we get y ≈ 0.5 + 1 = 1.5.
Therefore, the approximate value of y at x=2
The local linearization of the curve can be used to approximate the value of y at x=2. Substituting x=2 into the equation, we get y ≈ 1.5, which is the approximate value of y at x=2.
Learn more about slope here
https://brainly.com/question/3605446
#SPJ4
Decide whether or not the method of undetermined coefficients can be applied to find a particular solution of the given equation. 60''(x) - 70(x) = 4x sin 2x + 4x cos 2x Choose the correct answer below. O O Yes No
Answers
Yes, the method of undetermined coefficients can be applied to find a particular solution of the given equation.
To determine whether the method of undetermined coefficients can be applied to find a particular solution of the given equation, we need to consider the form of the complementary solution.
The method of undetermined coefficients is applicable when the complementary solution to the homogeneous equation does not contain any terms that are similar to the particular solution we are seeking. In other words, the particular solution should be a linearly independent solution.
The homogeneous equation associated with the given differential equation is 60''(x) - 70(x) = 0.
To determine if the method of undetermined coefficients can be applied, we need to analyze the terms on the right-hand side of the equation: 4x sin(2x) and 4x cos(2x).
Since the complementary solution to the homogeneous equation does not contain terms of the form x sin(2x) or x cos(2x), the method of undetermined coefficients can be applied to find a particular solution.
Therefore, the correct answer is "Yes."
To learn more about undetermined coefficients here:
https://brainly.com/question/31477302
#SPJ4
In exceed codes 11-14 solve the system of nonlinear equations using the graph (picture attached)

Answers
11. (-4, 1)
12. No solution
13. (1, 4) and (9, 4)
14. (-4, 0) and (1, 5)