teresa wants to make some cookies the recipe calls for 5 eggs and 10 tablespoons of butter but she only has 3 eggs she needs to know if she has enough butter to make the cookies with only three eggs how much butter will she need
Answers
Answer:
I think Teresa needs 6 tablespoons of butter..
Step-by-step explanation:
Hope this right...but if it's not,im so sorry
Related Questions
Help me with this plss
If x^2+1/x^2\(x^{2} +\frac{1}{x^2}=10; then x+\frac{1}{x}=?\)
Answers
(x + 1/x)² = x ² + 2 + 1/x ² = 10 + 2 = 12
==> x + 1/x = ±√12
A 10-ft ladder leans against the side of a house. The bottom of the latter is 5 ft from the side of the house. How high is the top of the ladder from the ground. If necessary, round your answer to the nearest tenth.
PLEASE HELP
Answers
Answer:
8.7 feet
Step-by-step explanation:
Pythagorean Theorem : 10 is hypotenuse and 5 is opposite. 10^2-5^2=75. Now take 75 and square root it and you will approximately get 8.7.
how many driving lessons do you need to do with a professioanl instructor before my parents could teach me
Answers
The number of driving lessons you need to take with a professional instructor before your parents can teach you varies depending on the regulations in your area. In some regions, a specific number of driving lessons is required by law before you can apply for your driver's license. As a result, you should check with your local Department of Motor Vehicles (DMV) or other regulatory agency to learn more about the specific requirements in your area.
In general, however, it is usually beneficial to take as many driving lessons as possible with a professional instructor. Professional driving instructors have been educated in how to teach driving skills safely and effectively. They have also assisted many other people in learning how to drive, and as a result, they have a wealth of knowledge and expertise to draw on.
The more driving lessons you take with a professional instructor, the more chances you'll have to learn and improve your driving abilities. You may be able to practice with your parents after only a few lessons, but it's generally a good idea to take as many as possible with an instructor before doing so. This will give you the best chance of success while you learn to drive safely and confidently.
To learn more about driving :
https://brainly.com/question/2619161
#SPJ11
We should use a normal distribution to model the number of years until the next florida hurricane strike.
a. True
b. False
Answers
Normal distribution to model the number of years until the next florida hurricane strike is false.
According to this statement
we have to find that the given statement is a true or a false.
So, For this purpose, we know that the
Normal distribution, is a probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean.
And
It accurately describes the distribution of values for many natural phenomena.
So,
A normal distribution to model the number of years until the next florida hurricane strike is not a perfect.
this is a false. because this is not applicable.
So, Normal distribution to model the number of years until the next florida hurricane strike is false.
Learn more about Normal distribution here
https://brainly.com/question/4079902
#SPJ4
Write the first six terms of the arithmetic sequence with the first term, a1, and common difference, d.
a1 = 2, d=3
Answers
Answer:
2.5.8.11.14.17
Step-by-step explanation:
Start from 2 and add 3 every time
Which equation models a line that is perpendicular to y = x - 1 and goes through the point (5,4)
Answers
Answer:
y = - x + 9
Step-by-step explanation:
Because the line is perpendicular, the slope with be the opposite reciprocal. So, if the slope is 1 as in the equation y = x - 1, the opposite reciprocal is -1.
So the equation that is perpendicular will look like this so far:
y = -x + b (b represents our y-intercept that we have not found yet)
Now we will find the y-intercept. We can find it by substituting the coordinates (5,4) as x and y into the equation right above ^^.
So, 4 = -(5) +b or 4 = -5 + b
Add 5 to both sides to isolate b on the right side. b = 9
Therefore, the y-intercept is 9.
Now we have found everything we need for the equation, which is
y = - x + 9
simplify 6a+5w-2a+w .....,,.,,.,..,..,,
Answers
Step 1:
Simplify A’s
6a - 2a = 4a
Step 2:
Simplify Ws
5w + w = 6w
Step 3:
Put together
4a + 6w
What does an inverse function look like?
Answers
Inverse functions are indicated by the symbol \(f^{-1}\) and are functions whose inverse is the function itself (x).
A function takes in values, applies specific operations to them, and produces an output. The inverse function acts, agrees with the outcome, and returns to the initial function. The inverse function, which also returns the beginning value, returns the result of a function.
The relationship that results from swapping out an independent variable for a variable that depends on a given equation, and which may or may not be a function. Consider the inverse relationship between the functions f and g: f(g(x)) = g(f(x)) = x.
To learn more about Inverse here:
https://brainly.com/question/2541698
#SPJ4
help me please thank you

Answers
Answer: The answer is y=-2x+5
any luck of help? pls say yess I'll brainlist u!!! give u 5 star just help me answer

Answers
Answer:
11. A) x = 0
y = 2x + 5
=> y = 2 * 0 + 5
=> y = 0 + 5 = 5
=> y = 5 (First blank)
x = 1
y = 2x + 5
=> y = 2 * 1 + 5
=> y = 2 + 5 = 7
=> y = 7 (Second blank)
x = 2
y = 2x + 5
=> y = 2 * 2 + 5
=> y = 4 + 5
=> y = 9 (Third blank)
x = 3
y = 2x + 5
=> y = 2 * 3 + 5
=> y = 6 + 5
=> y = 11 (Fourth blank)
x = 4
=> y = 2x + 5
=> y = 2 * 4 + 5
=> y = 8 + 5
=> y = 13 (Fifth blank)
11. B) x = 0
=> y = \(3x^{2} + 1\)
=> y = 3 * 0 * 0 + 1
=> y = 0 + 1
=> y = 1 (First blank)
x = 1
=> y = \(3x^{2} + 1\)
=> y = 3 * 1 * 1 + 1
=> y = 3 + 1
=> y = 4 (Second blank)
x = 2
=> y = \(3x^{2} + 1\)
=> y = 3 * 2 * 2 + 1
=> y = 12 + 1
=> y = 13 (Third blank)
x = 3
=> y = \(3x^{2} + 1\)
=> y = 3 * 3 * 3 + 1
=> y = 27 + 1
=> y = 28 (Fourth blank)
x = 4
=> y = \(3x^{2} + 1\)
=> y = 3 * 4 * 4 + 1
=> y = 48 + 1
=> y = 49 (Fifth blank)
For more info, here's a picture,
If my answer helped, kindly mark me as the Brainliest!!
Thank You!!

Ben paid $45 for an old guitar. He cleaned the guitar then resold it after marking up the price 15%. He used 36% of the money he got for the guitar to buy books. How much money did Ben spend on books?
Answers
Answer: I couldn't help you,but here's the answer. I'm not the bot the bot doens't have a cute anime chacter as their profile pic.
https://www.chegg.com/homework-help/questions-and-answers/ben-paid-45-old-guitar-cleaned-guitar-resold-marking-price-15--used-36-money-got-guitar-bu-q66963289
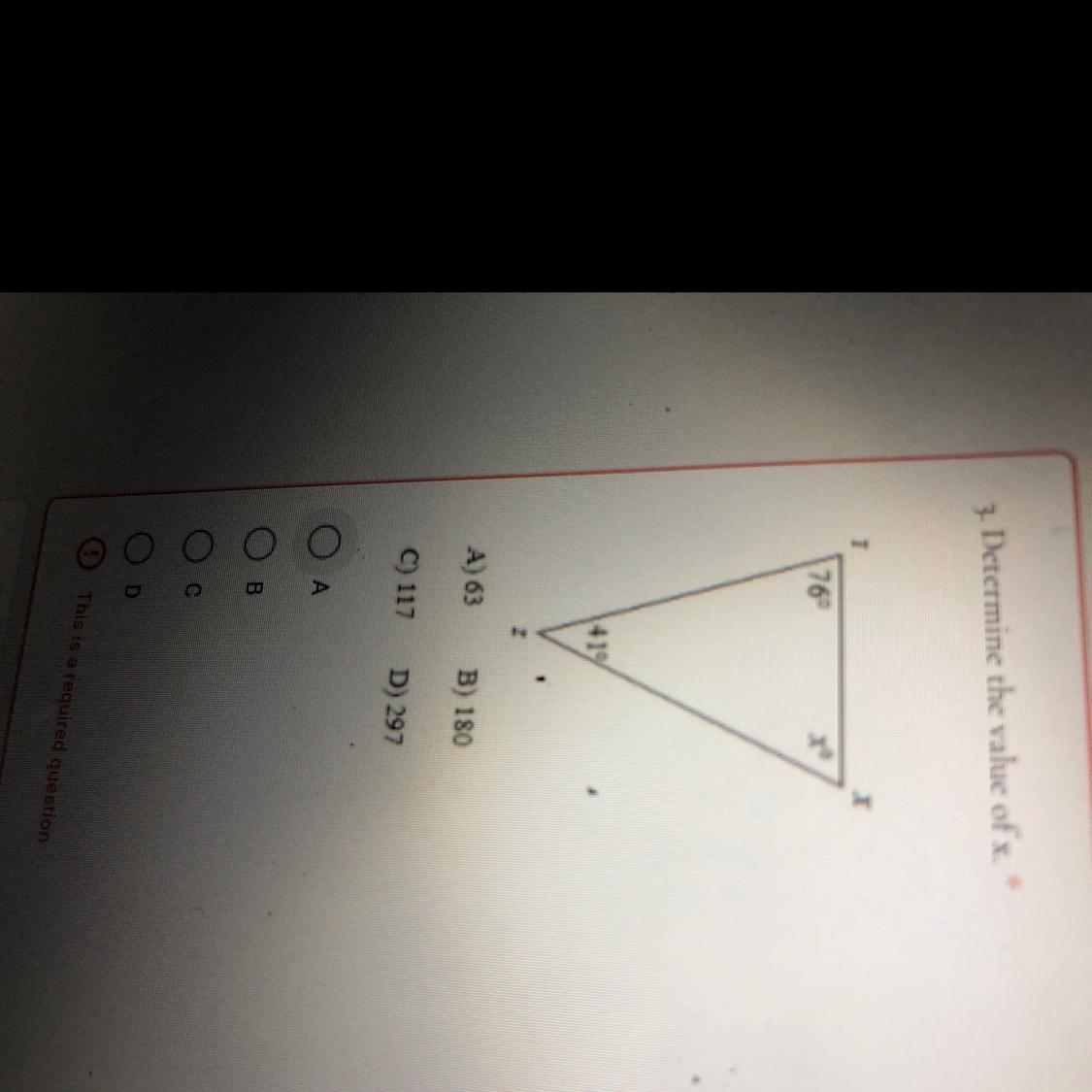
Detirme the value of x
Answers
The total value of a triangle's angles is 180*
so x=180-y-z
x=180-76-41
x=63*
hope it helps
prove that sum of angles of a convex plygon of n sides is (n-2)pi, where n>3
Answers
The IH states that the sum of the angles in convex polygon C(which, by the IH, is (n - 2)·π) and the sum of the angles in triangle B (180°) is the same as the sum of the angles in A.
Using induction all convex polygons with n vertices have angles that add to (n - 2)·π, therefore let P(n) be that. We will demonstrate that P(n), where n≥3, holds for every n ∈ N. We demonstrate P(3), which states that any convex polygon with three vertices has an angle total of 180 degrees. Any triangle formed by such a polygon has angles that add up to 180°.
Assume that P(n) holds for some n ≥ 3 and that all convex polygons with n vertices have angles that add to (n-2) 180° for the inductive step. We demonstrate P(n+1), which states that each convex polygon with n+1 vertices has an angle sum of (n-1)·π. Let A represent any n+1-vertex convex polygon.
The IH states that the sum of the angles in convex polygon C (which, by the IH, is (n - 2)·π) and the sum of the angles in triangle B (180°) is the same as the sum of the angles in A. As a result, the total angle in A is (n-1) 180°. Thus, the induction is complete and P(n + 1) holds.
To learn more about angles in convex polygon link is here
brainly.com/question/13585442
#SPJ4
write the polynomial in standard form then name the polynomial based on its degree and number of terms
Answers
a) The polynomial written in standard form is -4x^3 + x + 7.
b) It is a cubic polynomial because it has three terms and a degree of 3.
A polynomial is an expression consisting of variables and coefficients, where the variables are raised to non-negative integer powers and the coefficients are constants. The degree of a polynomial is the highest power of the variable in the polynomial. For example, in the polynomial -4x^3 + x + 7, the degree is 3 because the highest power of x is 3.
The standard form of a polynomial is when the terms are arranged in descending order of their degrees. This means that the term with the highest power of the variable is written first, followed by the next highest power, and so on, until the constant term is written last. In the case of -4x^3 + x + 7, we rearranged the terms so that the -4x^3 term is first, followed by the x term, and then the constant term of 7.
Finally, we can name the polynomial based on its degree and number of terms. In this case, we have a polynomial with three terms and a degree of 3, so it is called a cubic polynomial.
Learn more about polynomial here
brainly.com/question/29074766
#SPJ4
The given question is incomplete, the complete question is:
Write the polynomial in standard form then name the polynomial based on its degree and number of terms. x+ 7 - 4x^3
Yes or no awnser pls

Answers
Answer:
No the question iant a function
i.) Two fair dice are thrown.What is the probability that the sum of the two numbers thrown is a prime number?
ii.) A bag contains 10 pink balls, 7 white balls, and 4 blue balls. Three balls are drawn randomly from the bag one by one without replacement. What is the probability that there are exactly two balls of the same color?
Answers
i) The probability that the sum of two numbers thrown with fair dice is a prime number is 15/36, which simplifies to 5/12. ii) The probability of drawing exactly two balls of the same color when three balls are drawn randomly without replacement from a bag containing 10 pink balls, 7 white balls, and 4 blue balls is 39/91.
i) To find the probability that the sum of two numbers thrown with fair dice is a prime number, we need to determine the number of favorable outcomes and the total number of possible outcomes. The favorable outcomes are (2, 3), (3, 2), (2, 5), (5, 2), (3, 4), (4, 3), (5, 6), and (6, 5), which amounts to 8 possibilities. The total number of possible outcomes is 6 x 6 = 36 since each die has 6 faces. Therefore, the probability is 8/36, which simplifies to 2/9.
ii) When three balls are drawn randomly without replacement, we need to consider different cases to calculate the probability of drawing exactly two balls of the same color.
The possible cases are: (pink, pink, not pink), (white, white, not white), (blue, blue, not blue).
For each case, we calculate the probability as follows:
(pink, pink, not pink): (10/21) x (9/20) x (11/19)
(white, white, not white): (7/21) x (6/20) x (14/19)
(blue, blue, not blue): (4/21) x (3/20) x (17/19)
Then, we sum up the probabilities of all cases: [(10/21) x (9/20) x (11/19)] + [(7/21) x (6/20) x (14/19)] + [(4/21) x (3/20) x (17/19)], which simplifies to 39/91.
Therefore, the probability of drawing exactly two balls of the same color is 39/91.
Learn more about possible outcomes here:
https://brainly.com/question/29181724
#SPJ11
40 is what percent of 800?
Answers
Answer:
40/100 × 800
council the zeros
40× 8/1
320
Answer:
20%
Step-by-step explanation:
8/40 =x%/100%
800%/40=40x%/40
20=x%
x=20%
PLZZZZ HELP ME ,Plsss

Answers
Answer:
V = 72 ft³
Step-by-step explanation:
V = (3 x 8 x 2) + (4 x 2 x 3) = 72 ft³
Answer:
Try 1,152
Step-by-step explanation:
I think you have to multiply all the numbers and get 1,152. I'm not that good at math but.
F(x)= 2x^2-3x-9 G(x)= 4x^2-9 find (f/g) (x)
Answers
This is about division of polynomials.
(f/g)(x) = (x + 1)/(2x + 3)
(f/g) (x) simply means we divide f(x) by g(x) We are given;f(x) = 2x² - 3x - 9
g(x) = 4x² - 9
To divide this, let's simplify each function to its factors using the sun-product pattern.f(x) = 2x² - 3x + 6x - 9
Let's collect like terms;
f(x) = x(2x - 3) + 1(2x - 3)
Rewriting in factored form gives;
f(x) = (x + 1)(2x - 3)
Similarly;g(x) = 4x² - 9
g(x) = 4x² + 6x - 6x - 9
g(x) = 2x(2x + 3) - 3(2x + 3)
Rewriting in factored form gives;
g(x) = (2x + 3)(2x - 3)
Thus;
(f/g)(x) = ((x + 1)(2x - 3))/((2x + 3)(2x - 3))
(f/g)(x) = (x + 1)/(2x + 3)
Read more at;
brainly.in/question/37643694
The weights of certain machine components are normally distributed with a mean of 8.61 g and a standard deviation of 0.07 g. Find the two weights that separate the top 3% and the bottom 3%. Theses weights could serve as limits used to identify which components should be rejected. Answer 1. 8.46 g and 8.80 g 2. 8.58 g and 8.64 g 3. 8.60 g and 8.62 g
Answers
The correct answer is option 1: 8.46 g and 8.80 g. The given information is: The weights of certain machine components are normally distributed with a mean of 8.61 g and a standard deviation of 0.07 g. We need to find the two weights that separate the top 3% and the bottom 3%.Solution:The given distribution is a normal distribution, which is continuous and symmetric about its mean µ= 8.61 g. The standard deviation is given as σ= 0.07 g. Here, it is required to calculate the two weights that separate the top 3% and the bottom 3%.
Here, we can use the Z-score formula which is given by: Z = (X - µ)/σWhere, Z is the standardized score; X is the raw score or variable, µ is the mean of the population, and σ is the standard deviation of the population.Using the Z-score formula, we can find the Z-scores for the given data as follows: For top 3%, the Z-score is Z₃ = 1.88 (approx.)For bottom 3%, the Z-score is Z₁ = -1.88 (approx.)
The value of Z is calculated using the Z-table, which gives the area to the left of the Z-score. Since the area required is in the tails of the distribution, we can calculate it using the following relation:area in the tail = (100% - desired area)/2area in the tail = (100% - 3%)/2 = 48.5%Using the Z-score formula, we can find the two weights that separate the top 3% and the bottom 3% as follows:X = Zσ + µFor top 3%: X₃ = Z₃σ + µ = 1.88(0.07) + 8.61= 8.80 g (approx.)X₁ = Z₁σ + µ = -1.88(0.07) + 8.61= 8.46 g (approx.)Therefore, the two weights that separate the top 3% and the bottom 3% are 8.46 g and 8.80 g.
To know more about distributed visit:-
https://brainly.com/question/29332830
#SPJ11
can someone tell me how much is 0,5-⁶?
Answers
Answer:
add this and (5 × 5 × 5) × (5 × 5 × 5 × 5 × 5
Step-by-step explanation:
how many 0's are located to the right of the decimal point and before the first non-zero digit in the terminating decimal representation of $\frac{1}{2^5\cdot5^8}$?
Answers
There are 11 zeros in the given fraction's terminating decimal representation.
To determine the number of zeros to the right of the decimal point and before the first non-zero digit in the terminating decimal representation of \($\frac{1}{2^5\cdot5^8}$\) , we need to simplify the fraction.
\($\frac{1}{2^5\cdot5^8}$\) can be rewritten as \($\frac{1}{32\cdot390625}$\) .
To find the decimal representation of this fraction, we divide 1 by the product of the denominators: \($32\cdot390625$\) .
Performing the division, we get:
\($0.000000000000512$\)
In this decimal representation, there are 11 zeros located to the right of the decimal point and before the first non-zero digit, which is 5. Therefore, there are 11 zeros in the given fraction's terminating decimal representation.
To know more about decimal refer here:
https://brainly.com/question/30958821
#SPJ11
"Find f and f fx= f₁ = f(x, y) = 8x In xy A
Find the indicated maximum or minimum value of f subject to the given constraint. Minimum: f(x,y) = 6x +y + 2xy + 11x + 2y: y = x + 1 The minimum value is"
Answers
Minimum value of f(x,y) = f(-19/4, -15/4) = 17(-19/4) + 3(-15/4) + 2(-19/4)(-15/4)= -551/16 . Thus, the minimum value of f(x,y) under the given constraint is -551/16.
Given the function fx = f₁ = 8x in xy. Now, find the indicated maximum or minimum value of f subject to the given constraint: Minimum: f(x,y) = 6x + y + 2xy + 11x + 2y:
y = x + 1For finding the minimum value of f(x,y) under the given constraint y = x + 1, we first need to express f(x,y) in terms of x and y.
So, we have: f(x,y) = 6x + y + 2xy + 11x + 2y= 17x + 3y + 2xyWe need to minimize f(x,y) subject to the constraint y = x + 1.
Let's substitute y = x + 1 in f(x,y) = 17x + 3y + 2xy to get a new function f(x):
f(x) = 17x + 3(x+1) + 2x(x+1)= 19x + 3 + 2x²
Now, we have to minimize f(x) to get the minimum value of f(x,y) under the given constraint.
To find the minimum value of f(x), we differentiate f(x) w.r.t x and equate the derivative to zero:
f'(x) = 19 + 4x = 0⇒ x = -19/4We also need to check whether x = -19/4 is a point of maximum or minimum.
For this, we differentiate f'(x) w.r.t x:f''(x) = 4 > 0As f''(x) > 0 for all x, the function f(x) has a minimum value at x = -19/4.
Substituting x = -19/4 in f(x) = 19x + 3 + 2x², we get the minimum value of f(x,y) under the given constraint:
y = x + 1⇒ y = -19/4 + 1 = -15/4
Minimum value of f(x,y) = f(-19/4, -15/4) = 17(-19/4) + 3(-15/4) + 2(-19/4)(-15/4)= -551/16
Thus, the minimum value of f(x,y) under the given constraint is -551/16.
To know more about Constraint visit :
https://brainly.com/question/32636996
#SPJ11
Simplify the following polynomial
(3y^2- 4y+1)(-y^2+y-2
Answers
Answer:
-3y^4+7y^3-11y^2+9y-2
6. Find d.
Please help

Answers
Answer:
Step-by-step explanation:
The first thing we are going to do is to fill in the other angles that we need to solve this problem. You could find ALL of them but all of them isn't necessary. So looking at the obtuse angle next to the 35 degree angle...we know that those are supplementary so 180 - 35 = the obtuse angle in the small triangle. 180 - 35 = 145. Within the smaller triangle we have now the 145 and the 10, and since, by the Triangle Angle-Sum Theorem all the angles have to add up to equal 180, then 180 - (10 + 145) = the 3rd angle, so the third angle is 180 - 155 = 25. Now let's get to the problem. If I were you, I'd draw that out like I did to keep track of these angles cuz I'm going to name them by their degree. In order to find d, we need to first find the distance between d and the right angle. We'll call that x. The reference angle is 35, the side opposite that angle is 12 and the side we are looking for, x, is adjacent to that angle. So we will use the tan ratio to find x:
\(tan(35)=\frac{12}{x}\) Isolating x:
\(x=\frac{12}{tan(35)}\) so
x = 17.1377 m
Now we have everything we need to find d. We will use 25 degrees as our reference angle, and the side opposite it is 12 and the side adjacent to it is
d + 17.1377, so that is the tan ratio as well:
\(tan(25)=\frac{12}{d+17.1377}\) and simplifying a bit:
\(d+17.1377=\frac{12}{tan(25)}\) and a bit more:
d + 17.1377 = 25.73408 so
d = 8.59, rounded
at the beginning of an experiment, a scientist has 288 grams of radioactive goo. after 120 minutes, her sample has decayed to 4.5 grams. what is the half-life of the goo in minutes? find a formula for g ( t ) , the amount of goo remaining at time t . g ( t )
Answers
The half-life of the goo in minutes is 20 minutes.
Initailly the amount of radioactive goo is 288 grams
Time taken is 120 minutes
amount of radioactive goo left is 4.5 gram
Number of half lives =
\((\frac{1}{2})^{n} = \frac{a}{a'} \\\\\frac{1}{2^n} = \frac{4.5}{288}\\\\ \frac{1}{2^n} = \frac{1}{64}\)
2ⁿ = 64
2ⁿ = 2⁶
n = 6
The number of half lives is 6
half life = total time / number of half lives
= 120 / 6
= 20 minutes
Therefore, if at the beginning of an experiment, a scientist has 288 grams of radioactive goo. after 120 minutes, her sample has decayed to 4.5 grams, then the half-life of the goo in minutes is 20 minutes.
To learn more about half life refer here
https://brainly.com/question/26148784
#SPJ4
write the following expression without negative exponents and without parentheses (-9x)^-2
Answers
The value of the expression is 1/(9x)^2
How to evaluate the expressionFrom the question, we have the following parameters that can be used in our computation:
(-9x)^-2
We can write the expression without negative exponents by using a fraction with a positive exponent:
(-9x)^-2 = 1/(-9x)^2
And without parentheses, this expression becomes:
1/(9x)^2
Read more about expression at
https://brainly.com/question/15775046
#SPJ1
ABC has machines B₁, B₂ and B3 in manufacturing roofing sheets and B3 make 30%, 45% and 25% respectively of the roofing sheets. It is know from past experience that 2%, 3%, and 2% of the products made by B₁, B2 an respectively, are defective. With the help of this information, if a finished p is randomly selected, what is the probably that it is defective? Suppose a re sheet is randomly selected found to be defective, what is the probability th made by machine B3?
Answers
The probability of selecting a defective roofing sheet from the finished products of ABC is 2.45%. If a randomly selected defective sheet is found, the probability that it was made by machine B3 is approximately 54.55%.
To determine the probability of selecting a defective roofing sheet from the finished products of ABC, we need to calculate the weighted average of the defect rates for each machine.
The weighted average defect rate is calculated by multiplying the defect rate of each machine by its corresponding proportion of production and summing the products.
Weighted Average Defect Rate = (0.02 * 0.30) + (0.03 * 0.45) + (0.02 * 0.25)
= 0.006 + 0.0135 + 0.005
= 0.0245
Therefore, the probability of selecting a defective roofing sheet from the finished products of ABC is 2.45%.
To calculate the probability that a randomly selected defective sheet was made by machine B3, we need to consider the proportion of defective sheets contributed by B3 out of the total defective sheets.
The proportion of defective sheets from B3 = (0.02 * 0.30) / 0.0245
= 0.006 / 0.0245
≈ 0.245
The probability that a defective sheet was made by machine B3 can be obtained by dividing the proportion of defective sheets from B3 by the overall probability of selecting a defective sheet.
Probability of sheet made by B3 = (0.245 / 0.0245) * 100
≈ 54.55%
Therefore, if a randomly selected defective roofing sheet is found, the probability that it was made by machine B3 is approximately 54.55%.
To learn more about probability Click Here: brainly.com/question/31828911
#SPJ11
If angle A = 30 degree and AB =8 how long is bc
Answers
In a right angled triangle ABC, if angle A
= 30 degree and AB = 8 cm then the length of side BC is equals to the 4.62 cm.
As we see in figure, ∆ABC is an right angled triangle with side length of AB
= 8 cm and measure of angle A = 30°. Measure of angle B is 90°. So, measure of angle C = 180° - 90° - 30°
= 69°. So, AB is the opposite side for the angle C, AC is the opposite side for the angle B and BC opposite side for the angle A. We have to determine the length of side BC. Using the Trigonometric functions, tan x = height / base length
In ∆ABC, tan A = BC/AB
=> tan(30°) = BC/8
=> 1/√3 = BC/8 ( tan(30°) = 1/√3)
=> BC = 8/√3 = 4.62
Hence, required length of side BC is 4.62 cm.
For more information about right angled triangle, visit :
https://brainly.com/question/64787
#SPJ4
Complete question:
In triangle ABC, angle A=30 degrees and AB =8cm. Find the length of side BC? see the above figure.

35 points easy question
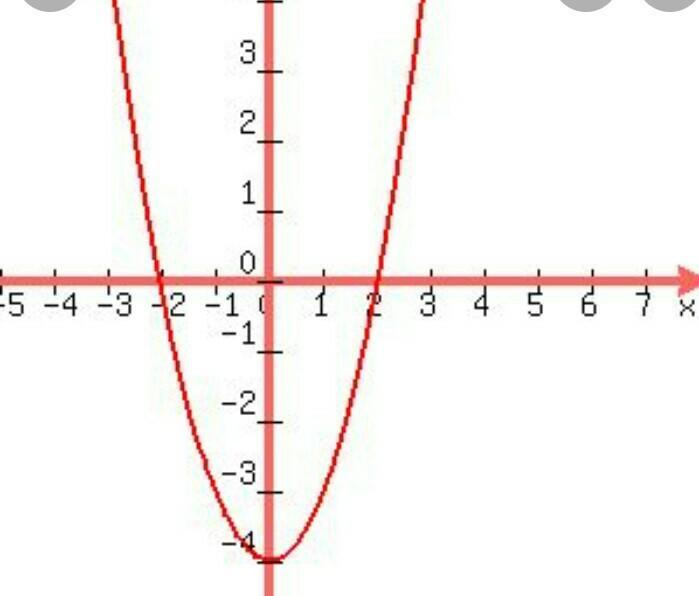
Let f(x)=x^2+4
Write a function g whose graph is a reflection in the y-axis of the graph of f.
Answers
Answer:
f-2(x) = \(\sqrt{x} -4\), - \(\sqrt{x} -4\)
Step-by-step explanation:
Answer:
\(y = \frac{15}{4} \\ \\ \)
it