tell me the answer on this question pleaseWhat is the range of the data below?
A box-and-whisker plot. The number line goes from 50 to 100. The whiskers range from 52 to 93, and the box ranges from 60 to 89. A line divides the box at 82.
22
28
42
Answers
Answer:
41
Step-by-step explanation:
93-52=41
Related Questions
PLS HELP ME WITH THESE 3 QUESTIONS



Answers
Answer:
1: -3
2: A&C
3: y = 4x + 1
Step-by-step explanation:
Answer:
-3
a and c
y=4x+1
Step-by-step explanation:
A box has three cards numbered 1, 2, and 3 A bag has three balls labeled A, B, and C Felipe will randomly pick a card from the box and record the number chosen. Then he will randomly pick a ball from the bag and record the letter chosen. Give the sample space describing all possible outcomes. Then give all of the outcomes for the event that the letter chosen is A.
Answers
The total number of possible outcomes for the event in which the letter chosen is A is 3.
A sample space is a set of all the possible outcomes that can be generated by performing a random experiment. Felipe chooses one card from the box, numbered 1, 2, or 3, and then he chooses a ball from the bag, labeled A, B, or C.
Hence, the number of possible outcomes is 3 x 3, or 9.
Below is the sample space describing all the possible outcomes:
{1A, 1B, 1C, 2A, 2B, 2C, 3A, 3B, 3C}
Now, we must find all the possible outcomes for the event in which the letter chosen is A.
Felipe picks a card from the box, numbered 1, 2, or 3.
If he selects card 1, he can then choose ball A, B, or C, resulting in three possible outcomes.
If he selects card 2, he can also select ball A, B, or C, resulting in another three possible outcomes.
If he chooses card 3, he can also choose ball A, B, or C, resulting in another three possible outcomes.
Hence, the total number of possible outcomes for the event in which the letter chosen is A is 3.
Learn more about sample space visit:
brainly.com/question/30206035
#SPJ11
What is the sign of −4 ÷ −8?
Answer?:
1: Positive
2: Negative
3: Zero
Answers
\(Hello\) \(There!\)
I believe the answer is...
2: Negative
Hopefully, this helps you!!
\(AnimeVines\)
what is the algebraic expression in terms of x,y and z for the area of the triangle with vertices (x,0,0), (0,y,0), and (0,0,z)?
Answers
The following algebraic expression must be satisfied:
s1 + s2 > s3.
s1 + s3 > s2.
s2 + s3 > s1.
The formula of the area of triangle in coordinate geometry is: A = (1/2)|x1 1 (y2 2 − y3 3 ) + x2 2 (y3 3 − y1 1 ) + x3 3 (y1 1 − y2 2 )|, where (x1 1 ,y1 1 ), (x2 2 ,y2 2 ), and (x3 3 ,y3 3 ) are the vertices of triangle.
xyz = x + y + z + 2 Add 1 + (zx + zy + xy) + (x + y + z) to both sides xyz + 1 + (zx + zy + xy) + (x + y + z) = 2x + 2y + 2z + 3 + zx + zy + xy Rearrange the terms on both sides : 1 + x + y + xy + z + zx + zy + xyz = 1 + y + z + yz + 1 + x + z + zx + 1 + x + y + xy ...
In this case, angle is equal to angle . Angles on a straight line sum to 180 degrees. This means that we can calculate the measure of angle by subtracting 122 from 180.
The area of a parallelogram is equal to the area of the rectangle on the same base and of the same altitude, i.e., between the same parallels. The area of a triangle is half the product of any of its sides and the corresponding altitude.
Therefore,
The following algebraic expression must be satisfied:
s1 + s2 > s3.
s1 + s3 > s2.
s2 + s3 > s1.
To learn more about Algebraic expressions visit:
brainly.com/question/4184022
#SPJ4
A cup has a circumference of 28 cm. Approximately what is the diameter?
Answers
Answer:
The diameter is approximately 8.9 cm
Step-by-step explanation:
The circumference is given by
C = pi *d
28 = pi *d
Divide each side by pi
28/pi = d
We can approximate pi by 3.14
28 /3.14 =d
8.917 = d
The diameter is approximately 8.9 cm
sec(pi/2 -x) =csc x true or false
Answers
Answer:
true
Step-by-step explanation:
if you rewrite \(sec\left(\frac{\pi }{2}\:-x\right)\) with trigonometric identities:
\(sec\left(\frac{\pi }{2}\:-x\right)\) \(=\frac{1}{\sin \left(x\right)}\)
\(\frac{1}{\sin \left(x\right)}\) \(=\csc \left(x\right)\)
so, yes, \(sec\left(\frac{\pi }{2}\:-x\right)\) \(=\csc \left(x\right)\)
hope this helps!!
solve the following: show your work

Answers
Answer:
I believe the answer is 1
Step-by-step explanation:
First follow the steps of PEMDAS:
Parenthesis -
1. 16 - 9 = 7
2. 4 - (-7) = 11
3. 17 - 9 = 8
Exponents -
There is no exponents
Multiplication/Division
1. -35/7 = -5
2. 48/8 = 6
Addition/Subtraction
1. -5 + 11 = 6
Finally, you wind up with 6/6 = 1
Express the function graphed
on the axes below as a piecewise function.

Answers
The required piece-wise function shown in the graph is y = x + 1 for x < 2 and y = 2x - 1 for x > 2.
To determine the equation of the given piece-wise function,
The equation of the function under x < 2 is given as,
y = x + 1 for x < 2
This equation can be obtained by locating two points on the line such as (-1, 0) and (0, 1), and forming an equation with these points,
Similarly,
For x > 2, we have
y = 2x - 1
Thus, the required piece-wise function shown in the graph is y = x + 1 for x < 2 and y = 2x - 1 for x > 2.
Learn more about piece-wise function here:
https://brainly.com/question/22051192
#SPJ1
5 (x-9) =55 A subtract 5 B divide 5 C add 9 D subtract 55
Answers
The operation carried out is divide 5. option B
What is an algebraic expression?An algebraic expression is described as an expression consisting of variables, terms, coefficients, constants and factors.
These algebraic expressions are also made of arithmetic or mathematical operations, such as;
DivisionMultiplicationAdditionSubtractionParenthesesBracket, etcFrom the information given, we have that;
5(x-9) =55
Divide both sides by 5, we have;
x - 9 = 55/5
Find the value
x - 9 = 11
collect like terms
x = 11 + 9
x = 20
Hence, the value is 20
Learn more about algebraic expressions here:
https://brainly.com/question/4344214
#SPJ1
I need some help please. Given the functions, complete the sections. a) Find the intercepts with the axes. b) Indicate the basic function that you will use to graph it. c) Identify the transformations that your graph will undergo, starting from its basic function. d) Draw the sketch showing the transformations, taking into account all the previous sections. Highlight f(x) with a pen or marker. e) Determine its domain and range.\(f(x) = - \frac{1}{4} \sqrt{8 - 4x} + 1\)
Answers
a)
The x-intercept can be found as:
\(\begin{gathered} f(x)=0 \\ so\colon \\ -\frac{1}{4}\sqrt[]{8-4x}+1=0 \\ -\frac{1}{4}\sqrt[]{8-4x}=-1 \\ \sqrt[]{8-4x}=4 \\ 8-4x=16 \\ 4x=8-16 \\ 4x=-8 \\ x=-\frac{8}{4} \\ x=-2 \end{gathered}\)Therefore, the x-intercept is: (-2,0)
The y-intercept can be found evaluating the function for x = 0, so:
\(\begin{gathered} f(0)=-\frac{1}{4}\sqrt[]{8-4(0)}+1 \\ f(0)=1-\frac{\sqrt[]{2}}{2} \\ f(0)\approx0.29 \end{gathered}\)b) The parent function for this is given by:
\(g(x)=\sqrt[]{x}\)c)
1st: A reflection over y-axis:
\(\begin{gathered} y=g(-x) \\ y=\sqrt[]{-x} \end{gathered}\)2nd: A horizontal compression:
\(\begin{gathered} y=g(-4x) \\ y=\sqrt[]{-4x} \end{gathered}\)3rd: A horizontal translation 8 units to the left:
\(\begin{gathered} y=g(x+8) \\ y=\sqrt[]{-4x+8}=\sqrt[]{8-4x} \end{gathered}\)4th: A reflection over y-axis:
\(\begin{gathered} y=-g(x) \\ y=-\sqrt[]{8-4x} \end{gathered}\)5th: A vertical compression:
\(\begin{gathered} y=\frac{1}{4}g(x) \\ y=-\frac{1}{4}\sqrt[]{8-4x} \end{gathered}\)6th: A vertical translation 1 unit up:
\(\begin{gathered} y=g(x)+1 \\ y=-\frac{1}{4}\sqrt[]{8-4x}+1 \end{gathered}\)d)
Where the blue graph is the parent function:
\(g(x)=\sqrt[]{x}\)And the red graph is the function after the transformations:
\(f(x)=-\frac{1}{4}\sqrt[]{8-4x}+1\)e)
The domain and the range are:
\(\begin{gathered} D\colon\mleft\lbrace x\in\R\colon x\le2\mright\rbrace \\ R\colon\mleft\lbrace y\in\R\colon y\le1\mright\rbrace \end{gathered}\)
Jenna has a collection of trading cards. She started her collection with 175 cards. She buys packs of cards that contain 15 cards each. Solve an inequality to determine how many packs of cards Jenna buys so that she will have over 400 cards in her collection.
Answers
Answer:
175 + 15x = 400
Step-by-step explanation: X= the pack of cards.
Jenna will have to buy 22 card packets to have more than 400 cards in the collection.
What is inequality?An inequality is used to compare two or more expressions or numbers.
For example -
2x > 4y + 3
x + y > 3
x - y < 6
Given is that Jenna has a collection of trading cards. She started her collection with 175 cards. She buys packs of cards that contain 15 cards each
Assume that she will have to buy {x} packets of cards to have over 400 cards. Then, we can write the inequality as -
400 < 175 + 15x
15x > 325
x > 325/15
x > 65/3
x > 21.8
x > 22 {approx.}
Therefore, Jenna will have to buy 22 card packets to have more than 400 cards in the collection.
To solve more questions on inequality, visit the link-
https://brainly.com/question/11897796
#SPJ2
Find the balance in the account with a principal of $4,100 earning 5% compounded monthly after 24 years.
Answers
Answer:
The formula is
A=p (1+r/k)^kt
A future value?
P present value 4100
R interest rate 0.04
K compounded monthly 12
T time 10 years
A=4,100×(1+0.04÷12)^(12×10)
A=6,112.41. ..answer
Step-by-step explanation:
inge flies a kite at a height of 300 ft, the wind carrying the kite horizontally away at a rate of 25 ftsec. how fast must she let out the string when the kite is 500 ft away from her?
Answers
20 ft/sec must she let out the string when the kite is 500 ft away from her.
What is rate?
A rate is a unique ratio where the two words are expressed in several units.
For instance, the price is 69 for 12 ounces if a 12-ounce can of maize costs 69. This is not a proportion of two comparable units, like shirts. Cents and ounces are the two dissimilar units in this ratio.
Let x = distance of girl from the point on the ground directly below the kite at time t
y = length of string at time t
At time t, we have a right triangle with horizontal leg of length x, vertical leg of length 300, and hypotenuse of length y.
Given: dx/dt = 25
Find: dy/dt when y = 500
By the Pythagorean Theorem, \(x^2 +300^2 = y^2\)
Differentiating both sides, with respect to t,
\((2x)\frac{dx}{dt} = 2y\frac{dy}{dt}\) ...(1)
Since, \(x^2 +300^2 = y^2\), y = 500,
So, x = 400
Plug these values in equation (1).
\(2(400)(25) = 2(500)\frac{dy}{dt}\)
After solving,
\(\frac{dy}{dt} = 20 ft/sec\)
Therefore, 20 ft/sec must she let out the string when the kite is 500 ft away from her.
To know more about the rate, click on the link
https://brainly.com/question/25793394
#SPJ4
Percentage:
A shop has 150 gaming pc. They sold 30.
Find the percentage of the PC that they have not sold.
Answers
If you cross multiply 30 w/ 100 and then divide it by 150 you will get 20.
the standard deviation is a parameter, but the mean is an estimator. T/F
Answers
The statement "the standard deviation is a parameter, but the mean is an estimator" is false. An estimator is a random variable that is used to calculate an unknown parameter. Parameters are quantities that are used to describe the characteristics of a population.
The standard deviation is a parameter, while the sample standard deviation is an estimator. Likewise, the mean is a parameter of a population, and the sample mean is an estimator of the population mean. Therefore, the statement is false because the mean is a parameter of a population, not an estimator. The sample mean is an estimator, just like the sample standard deviation. In statistics, parameters are values that describe the characteristics of a population, such as the mean and standard deviation, while estimators are used to estimate the parameters of a population.
The sample mean and standard deviation are commonly used as estimators of population mean and standard deviation, respectively. The mean is a parameter of a population, not an estimator. The sample mean is an estimator of the population mean, and the sample standard deviation is an estimator of the population standard deviation. The sample standard deviation is an estimator of the population standard deviation. In statistics, parameter estimates have variability because the sample data is a subset of the population data. The variability of the estimator is measured using the standard error of the estimator. In summary, the statement "the standard deviation is a parameter, but the mean is an estimator" is false because the mean is a parameter of a population, while the sample mean is an estimator.
To know more about deviation visit:
https://brainly.com/question/29758680
#SPJ11
a quality control inspector has drawn a sample of 16 light bulbs from a recent production lot. suppose 20% of the bulbs in the lot are defective. what is the probability that between 6 and 9 (both inclusive) bulbs from the sample are defective? round your answer to four decimal places.
Answers
The probability that between 6 and 9 (both inclusive) bulbs from the sample are defective is 0.5362
This is a binomial distribution problem, where the probability of success (defective bulb) is 0.2 and the probability of failure (non-defective bulb) is 0.8. We need to find the probability that between 6 and 9 (both inclusive) bulbs out of 16 bulbs in the sample are defective.
We can use the binomial probability formula to solve this problem
P(6 ≤ X ≤ 9) = P(X = 6) + P(X = 7) + P(X = 8) + P(X = 9)
where X is the number of defective bulbs in the sample.
P(X = k) = (n choose k) × p^k × (1-p)^(n-k)
where n is the sample size, k is the number of defective bulbs, p is the probability of a defective bulb, and (n choose k) is the binomial coefficient.
Using this formula, we can calculate the probability for each value of X and sum them up to get the probability for the range 6 to 9.
P(X = 6) = (16 choose 6) × 0.2^6 × 0.8^10 = 0.0881
P(X = 7) = (16 choose 7) × 0.2^7 × 0.8^9 = 0.1409
P(X = 8) = (16 choose 8) × 0.2^8 × 0.8^8 = 0.1606
P(X = 9) = (16 choose 9) × 0.2^9 × 0.8^7 = 0.1462
Therefore, the probability that between 6 and 9 (both inclusive) bulbs from the sample are defective is
P(6 ≤ X ≤ 9) = 0.0881 + 0.1409 + 0.1606 + 0.1462 = 0.5362
Learn more about probability here
brainly.com/question/29350029
#SPJ4
An engineer is designing a storage compartment in an aircraft. The compartment's volume is 72 cubic meters. The width is 2 meters longer than the length. The height is 1 meter less than the length. Find the dimensions of the compartment.
Answers
An engineer is designing a storage compartment in an aircraft. The compartment's volume is 72 cubic meters. The width is 2 meters longer than the length. The height is 1 meter less than the length. the dimensions of the compartment are 4m × 6m × 3m.
Find the dimensions of the compartment. Solution:The volume of a rectangular prism is given by;\(`V= l × w × h`\) Given that the compartment's volume is 72 cubic meters, let's substitute\(`V = 72`\)
cubic meters;\(`l × w × h = 72`\)
We also know that;\(w = l + 2h = l - 1\)
Substituting w and h in terms of l, we get;\(`l(l+2)(l-1) = 72`\)Expanding,
we get;\(`l(l²-1) + 2(l²-1) = 72`\)
Simplifying, we get;\(`l³ + l² - 2l - 74 = 0`\)
We will use trial and error method to find one of the roots,`l= 4`.
By substitution, we get;\(w = 4 + 2 = 6m h = 4 - 1 = 3m\)
Thus, the compartment dimensions are 4m × 6m × 3m. The width is 6 meters, the length is 4 meters, and the height is 3 meters.
To know more about rectangular visit:
https://brainly.com/question/21416050
#SPJ11
If anyone can help it would be greatly appreciated. I will give you 20 extra points for free! Or venmo you $10 :)

Answers
Answer:
15) 1/3
18) 1/2
21) 25/26
Step-by-step explanation:
15) 2/6=1/3
18) 3/6=1/2
21) 25/26
help me with calculus
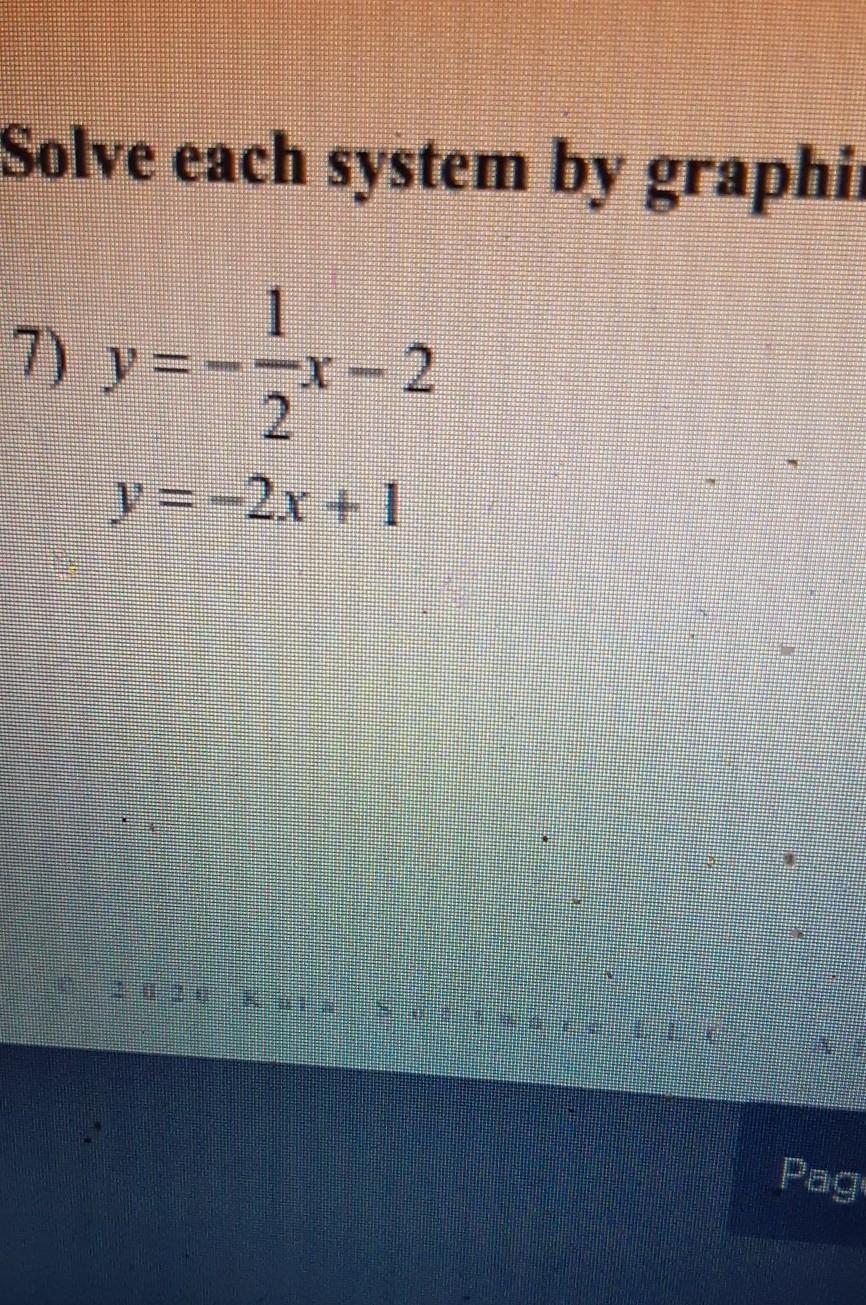
Answers
Answer:
(2, -3)
General Formulas and Concepts:
Algebra I
Reading a coordinate planeCoordinates (x, y)Solving systems of equations by graphingStep-by-step explanation:
Where the 2 lines intersect is the solution to the system of equations.

solve this equation p-3 1/6=-2 1/2
Answers
Answer:
p=2/3
Step-by-step explanation:
The value of p in the linear equation in one variable p - 3 1/6 = -2 1/2 is 2/3 or p = 2/3.
What is a linear equation?It is defined as the relation between two variables, if we plot the graph of the linear equation we will get a straight line.
If in the linear equation, one variable is present, then the equation is known as the linear equation in one variable.
It is given that:
The equation is:
p - 3 1/6 = -2 1/2
To solve the above linear equation in one variable first convert mixed fraction to fraction:
p - 19/6 = -5/2
p = -5/2 + 19/6
Take LCM of 2 and 6
p = (-15 + 19)/6
p = (4)/6
p = 2/3
Thus, the value of p in the linear equation in one variable p - 3 1/6 = -2 1/2 is 2/3 or p = 2/3.
Learn more about the linear equation here:
brainly.com/question/11897796
#SPJ2
Please help me I am bad at math!
Group the terms together and solve.
-6 -8c = 3c + 16
A. 242
B. -4.4
C. -2
D. 10/11
Sorry if this is easy
Answers
Answer:
I got C.
Step-by-step explanation:
Calculator.
Answer:
C. -2
Step-by-step explanation:
Subtract 3c from -8c, and add -6 to 16 to simplify the equation.

hey can anyone answer this please

Answers
Answer:
Your answer is F
Step-by-step explanation:
Philips amount is more than 200 but less than 300.
What is the range of this relation?
5
4
3
2
o
1
х
-5
-4
-3
-2
1
2
3
4
5
-1 0
-1
-2
-3
-4
5

Answers
Answer:
the answer is in the picture below
Step-by-step explanation:

does anyone know -4 = -6?
Answers
Answer:
-2
Step-by-step explanation:
I'm not sure but I think you just need to make them the same
what value of n make this equation true 12(n+6)=96
Answers
Answer:
2
Step-by-step explanation:
(6+2)x 12 =96
Answer:
2
Step-by-step explanation:
12(2+6)=96
12×8=96
I need 20 characters so yeah. Have a great day.
find f. f ''() = sin() cos(), f(0) = 2, f '(0) = 4
Answers
The function f(x) is given by f(x) = - (1/8) sin(2x) + 4x + 2
To find the function f(x), we need to integrate f''(x) twice and apply the given initial conditions.
Given f''(x) = sin(x)cos(x), f(0) = 2, and f'(0) = 4.
1. Integrate f''(x) with respect to x to find f'(x):
f'(x)=∫(sin(x)cos(x) dx) = ∫(1/2) sin2(x) = -1/4cos2x + C₁
i.e., f'(x)= -1/4cos2x + C₁
Apply the initial condition f'(0) = 4:
f'(0)= -(1/4)cos2(0) + C₁ = 4
C₁ = 17/4
So, f'(x) = -1/4cos2x + 4
2. Integrate f'(x) with respect to x to find f(x):
f(x)= ∫(-1/4cos2x + 4) dx = -1/8 sin2x + 4x + C₂
f(x)= -1/8 sin2x + 4x + C₂
Apply the initial condition f(0) = 2:
f(x)= -(1/8) sin(2*0) + 4(0) + C₂ = 2
C₂ = 2
So, the function f(x) is given by:
f(x) = - (1/8)sin(2x) + 4x + 2
To learn more about differentiation visit: brainly.com/question/31402754
#SPJ11
please help.it’s the second question. the one in the middle

Answers
Answer:
1,024
Step-by-step explanation:
Answer:
past number gets multiplied by 2 and so on
Step-by-step explanation:
2,4,8,16,32,64,128,256,512,1024
is u in the plane in set of real numbers rℝcubed3 spanned by the columns of a? why or why not?
Let u [-16 18 10] and A [2 -3 1 -4 5 1] Is u in the plane in R3 spanned by the columns of A? Why or why not? 10 Select the correct choice below and fill in the answer box to complete your choice. (Type an integer or decimal for each matrix element.) O A. No, the reduced row echelon form of the augmented matrix is which is an inconsistent system. O B. Yes, multiplying A by the vectorwrites u as a linear combination of the columns of A.
Answers
u in the plane in set of real numbers rℝcubed3 spanned by the columns, then the one solution matrix is, \(\left[\begin{array}{ccc}x_{1} &\\x_{2} &\\\end{array}\right]\) = \(\left[\begin{array}{ccc}2&\\6.66&\\\end{array}\right]\)
Given data,
Let u [-16 18 10] and A [2 -3 1 -4 5 1]
u in the plane in set of real numbers rℝcubed3 spanned by the columns of A,
So,
We can write,
u = \(\left[\begin{array}{ccc}-16&\\18&\\10&\end{array}\right]\) and A = \(\left[\begin{array}{ccc}2&-3\\1&-4\\5&1\end{array}\right]\)
Then,
AX = b
w = \(\left[\begin{array}{ccc}2&-3&-16\\1&-4&18\\5&1&10\end{array}\right]\)
A = \(\left[\begin{array}{ccc}2&-3\\1&-4\\5&1\end{array}\right]\)
null A = \(\left[\begin{array}{ccc}x_{1} &\\x_{2} &\\\end{array}\right]\)
\(\left[\begin{array}{ccc}2&-3\\1&-4\\5&1\end{array}\right]\) \(\left[\begin{array}{ccc}x_{1} &\\x_{2} &\\\end{array}\right]\)= \(\left[\begin{array}{ccc}0&\\0&\\0&\end{array}\right]\)
2\(x_{1}\) - 3\(x_{2}\) = 0
\(x_{1}\) - 4\(x_{2}\) = 0
5\(x_{1}\) + 1\(x_{2}\) = 0
We can solve the equations,
2\(x_{1}\) - 3\(x_{2}\) = 0
\(x_{1}\) - 4\(x_{2}\) = 0
-----------------------
\(x_{1}\) - 7\(x_{2}\) = 0
\(x_{1}\) = 7\(x_{2}\)
We can substitute \(x_{1}\) values,
2\(x_{1}\) - 3\(x_{2}\) = 0
2*7\(x_{2}\) - 3\(x_{2}\) = 0
\(14x_{2}\) - 3\(x_{2}\) = 0
11\(x_{2}\) = 0
\(x_{2}\) = 0
\(\left[\begin{array}{ccc}2&-3\\1&-4\\5&1\end{array}\right]\) \(\left[\begin{array}{ccc}x_{1} &\\x_{2} &\\\end{array}\right]\)= = \(\left[\begin{array}{ccc}-16&\\18&\\10&\end{array}\right]\)
2\(x_{1}\) - 3\(x_{2}\) = -16
\(x_{1}\) - 4\(x_{2}\) = 18
5\(x_{1}\) + 1\(x_{2}\) = 10
We can solve the matrix equations,
2\(x_{1}\) - 3\(x_{2}\) = -16
\(x_{1}\) - 4\(x_{2}\) = 18
--------------------------
\(x_{1}\) - 7\(x_{2}\) = 2
\(x_{1}\) = 2 + 7\(x_{2}\)
\(x_{1}\) = 2 + 7(0)
\(x_{1}\) = 2
2\(x_{1}\) - 3\(x_{2}\) = -16
2*2 - 3\(x_{2}\) = -16
4 - 3\(x_{2}\) = -16
- 3\(x_{2}\) = -16 - 4
- 3\(x_{2}\) = -20
3\(x_{2}\) = 20
\(x_{2}\) = 20/3
\(x_{2}\) = 6.66
Therefore,
u in the plane in set of real numbers rℝcubed3 spanned by the columns, then the one solution matrix is, \(\left[\begin{array}{ccc}x_{1} &\\x_{2} &\\\end{array}\right]\) = \(\left[\begin{array}{ccc}2&\\6.66&\\\end{array}\right]\)
To learn more about Matrix problems visit :
brainly.com/question/15892044
#SPJ4
Location is known to affect the number, of a particular item, sold by an auto parts facility. Two different locations, A and B, are selected on an experimental basis. Location A was observed for 13 days and location B was observed for 18 days. The number of the particular items sold per day was recorded for each location. On average, location A sold 39 of these items with a sample standard deviation of 8 and location B sold 55 of these items with a sample standard deviation of 2. Select a 90% confidence interval for the difference in the true means of items sold at location A and B
Answers
We have two samples, A and B, so we need to construct a 2 Samp T Int using this formula:
\(\displaystyle \overline {x}_1 - \overline {x}_2 \ \pm \ t^{*} \sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2} }\)In order to use t*, we need to check conditions for using a t-distribution first.
Random for both samples -- NOT STATED in the problem ∴ proceed with caution!Independence for both samples: 130 < all items sold at Location A; 180 < all items sold at Location B -- we can reasonably assume this is trueNormality: CLT is not met; n < 30 for both locations A and B ∴ proceed with caution!Since 2/3 conditions aren't met, we can still proceed with the problem but keep in mind that the results will not be as accurate until more data is collected or more information is given in the problem.
Solve for t*:
We need the tail area first.
\(\displaystyle \frac{1-.9}{2}= .05\)Next we need the degree of freedom.
The degree of freedom can be found by subtracting the degree of freedom for A and B.
The general formula is df = n - 1.
df for A: 13 - 1 = 12df for B: 18 - 1 = 17 df for A - B: |12 - 17| = 5Use a calculator or a t-table to find the corresponding t-score for df = 5 and tail area = .05.
t* = -2.015Now we can use the formula at the very top to construct a confidence interval for two sample means.
\(\overline {x}_A=39\) \(s_A=8\) \(n_A=13\) \(\overline {x}_B = 55\) \(s_B=2\) \(n_B=18\) \(t^{*}=-2.015\)Substitute the variables into the formula: \(\displaystyle \overline {x}_1 - \overline {x}_2 \ \pm \ t^{*} \sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2} }\).
\(39-55 \ \pm \ -2.015 \big{(}\sqrt{\frac{(8)^2}{13} +\frac{(2)^2}{18} } } \ \big{)}\)Simplify this expression.
\(-16 \ \pm \ -2.015 (\sqrt{5.1453} \ )\) \(-16 \ \pm \ 3.73139\)Adding and subtracting 3.73139 to and from -16 gives us a confidence interval of:
\((-20.5707,-11.4293)\)If we want to interpret the confidence interval of (-20.5707, -11.4293), we can say...
We are 90% confident that the interval from -20.5707 to -11.4293 holds the true mean of items sold at locations A and B.
Which sign makes the statement true?
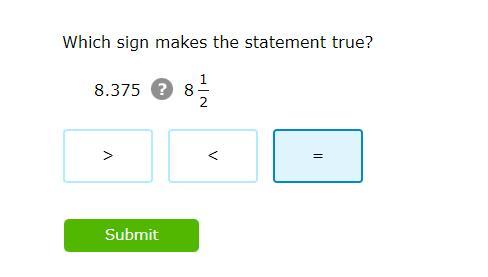
Answers
Answer: <
It is "<" because 8 1/2 as a decimal is 8.50 and the other decimal is 8.375. 8.50 is greater than 8.375.
Your welcome!
=^..^=
Answer:<
Step-by-step explanation:
8.375= \(8\frac{375}{1000} =8\frac{3}{80} \\\)
1/2=40/80
40/80>3/80
so,