Answers
Answer:
Option 4: f(2) ≠ 0, the binomial x-2 is not a factor of f(x).
Explanation:
Given the polynomial function:
\(f(x)=2x^3+x^2-5x+2\)We want to determine if x-2 is a factor of f(x) using the factor theorem.
By the Factor Theorem:
So, to check if x-2 is a factor of f(x), we first need to evaluate f(2).
\(\begin{gathered} f(x)=2x^{3}+x^{2}-5x+2 \\ f(2)=2(2)^3+(2)^2-5(2)+2 \\ =2(8)+4-10+2 \\ =16+4+2-10 \\ f(2)=12 \end{gathered}\)Since f(2) is not equal to 0, the binomial x-2 is not a factor of f(x).
The last option is correct.
Related Questions
Isosceles triangle has , and a circle with radius is tangent to line at and to line at . What is the area of the circle that passes through vertices , , and
Answers
The circle that passes through the vertices of triangle ΔABC (A, B, C) is the
circumscribing circle of triangle ΔABC.
The area of the circle that passes through vertices A, B, and C, is (C) 26·π
Reasons:
The given parameters are;
Side length of isosceles triangle ΔABC; \(\overline{AB}\) = \(\overline{AC}\) = 3·√6
Radius of circle tangent to \(\overline{AB}\) at B and \(\overline{AC}\) at C = 5·√2
Required:
Area of the circle that passes through vertices A, B, and C
Solution:
Angle ∠BAO is given as follows;
\(\angle BAO = arctan\left(\dfrac{5 \cdot \sqrt{2} }{3 \cdot \sqrt{6}} \right) = \mathbf{arctan\left(\dfrac{5 \cdot \sqrt{3} }{9} \right)}\)
Therefore;
\(\angle BOA = 90^{\circ} - arctan\left(\dfrac{5 \cdot \sqrt{3} }{9} \right)\)
\(\overline{BC} = 2 \times 5 \cdot \sqrt{2} \times sin\left(90^{\circ} - arctan\left(\dfrac{5 \cdot \sqrt{3} }{9} \right)\right) = 15\cdot \sqrt{\dfrac{6}{13} }\)
∠ABO' = ∠BAO' (Base angles of isosceles triangle ΔABO')
\(\angle BAO' = \angle BAO = \mathbf{arctan\left(\dfrac{5 \cdot \sqrt{3} }{9} \right)}\)
Therefore;
\(\angle BO'A = 180^{\circ} - 2 \times arctan\left(\dfrac{5 \cdot \sqrt{3} }{9} \right)\)
From sine rule, we have;
\(\dfrac{\overline{AB}}{sin \left(\angle BO'A \right)} = \mathbf{\dfrac{\overline{BO'}}{sin \left(\angle BAO' \right) \right)}}\)
Which gives;
\(\mathbf{\dfrac{3 \cdot \sqrt{6} }{sin \left( 180^{\circ} - 2 \times arctan\left(\dfrac{5 \cdot \sqrt{3} }{9} \right)\right)}} = \dfrac{\overline{BO'}}{sin \left(arctan\left(\dfrac{5 \cdot \sqrt{3} }{9} \right) \right)}\)
Using a graphing calculator, we get;
\(\overline{BO'} = \dfrac{3 \cdot \sqrt{6} }{sin \left( 180^{\circ} - 2 \times arctan\left(\dfrac{5 \cdot \sqrt{3} }{9} \right)\right)} \times sin \left(arctan\left(\dfrac{5 \cdot \sqrt{3} }{9} \right) \right) = \sqrt{26}\)
The radius of the circumscribing circle \(\overline{BO'}\) = √(26)
Therefore, area of the circumscribing circle, \(A_{O'}\) = π·(√(26))² = 26·π
The area of the circle that passes through vertices A, B, and C, is (C) 26·π
Learn more here:
https://brainly.com/question/17147358
The possible question options obtained from a similar question online are;
(A) 24·π (B) 25·π (C) 26·π (D) 27·π (E) 28·π

help me my shawtys
6 − x = −12

Answers
Answer:
D.18
Step-by-step explanation:
6-x=-12
-x=-12-6
-x=-18 divide both sides by -1
x=18
This is just a question I had.
If Denny (random name) left to another country and he left the Tuesday of this week (June 20) and he left for a month, what day would he be back on? I though July 18 but I’m not sure. Pls help?
Answers
Answer:
Step-by-step explanation:
Well, since the length of a month can vary in the number of days, this answer can also vary.
For example, February is only 28 days long, while December is 31 days long.
That being said, the average length of all 12 months is 30.436875 days, so if Denny left to another country on June 20th, he would most likely be back July 19th of July 20th.
I hope this helps!
Question 12 (1 point)
The degree of each term in the binomial expansion of (x - y)5 is
4
5
-5
6
.
Answers
=================================================
Explanation:
Let's consider the expression (x-y)^2. It expands out to x^2-2xy+y^2. The terms are:
x^2-2xyy^2Each of those terms either has a single variable with an exponent of 2, or has the exponents add to 2. Think of 2xy as 2x^1y^1.
In short, this means that the degree of each monomial term is 2.
----------
Now consider (x-y)^3. It expands out into x^3-3x^2y+3xy^2+y^3.
We have terms that either have a single variable and the exponent is 3, or the exponents add to 3. The degree of each term is 3.
----------
This pattern continues.
In general, for (x-y)^n, where n is any positive whole number, the degree of each term in the expansion is n. If you picked any term, added the exponents, then the exponents will add to n.
01:37:35
What is the difference between the largest prime number less than 50 and the smallest composite number greater than 10
Answers
Answer:
35
Step-by-step explanation:
47-12=35
2. The ramp above connects two vertical supports,
forming two similar triangles: AADE~ AABC. Side AC corresponds to which side in the other triangle?
Answer:
3. What is the length of side BC?

Answers
The side AC corresponds to the side AC in the other triangle and the length of BC is 15 units
Side AC corresponds to which sideFor two triangles to be similar, the corresponding sides of the triangles must be in proportion
Having said that
The side AC corresponds to the side AC in the other triangle
What is the length of side BC?The length BC is calculated as
BC/9 = 25/15
Express as products
So, we have
BC = 9 * 25/15
Evaluate the products
BC = 15
Hence, the length of BC is 15 units
Read more about similar triangles at
https://brainly.com/question/14285697
#SPJ1
Answer two questions about Systems A and B:
A: x−4y=1
5x+6y=−5
B: x=1+4y
5x+6y=−5
How can we get System B from System A?
A: Replace one equation with itself where a quantity is added to only one side
B: Replace one equation with itself where the same quantity is added to both sides
C: Swap only the right-hand sides of both equations
D: Swap the order of the equations
Based on the previous answer, are the systems equivalent? In other words, do they have the same solution?
A: Yes
B: No
Answers
Answer:
Replace one equation with itself where the same quantity is added to both sides
Yes
Yes, the systems are equivalent. In other words, they have the same solution.
What is a linear equation?A linear equation is an equation that has the variable of the highest power of 1. The standard form of a linear equation is of the form Ax + B = 0.
The Systems of equation given for A and B:
A: x−4y=1
5x+6y=−5
B: x=1+4y
5x+6y=−5
So, we get System B from System A by the following step;
A; Replace one equation with itself where the same quantity is added to both sides.
Hence, Yes the systems are equivalent. In other words, they have the same solution.
Learn more about linear equations;
https://brainly.com/question/10413253
#SPJ2
hello I need help understanding a slope and y-intercept math problem I need a tutor that will please allow me to ask for the question so I can better understand what I'm working on thank you

Answers
ANSWER
EXPLANATION
Slope is defined as the numerical value that determines the steepness of a line
Mathematically, slope is expressed below as
\(\text{ Slope = }\frac{\text{ rise }}{\text{ run}}\)Here is a scatter plot that shows the number of assists and points for a group of hockey players. The model, represented by y=1.5x+1.2 , is graphed with the scatter plot.a. What does the slope mean in this situation?b. Based on the model, how many points will a player have if he has 30 assists?
Answers
Based on the model, a player with 30 assists will have approximately 46.2 points.
a. The slope of a line in a scatter plot represents the relationship between the two variables being plotted. In this case, the slope of the model y = 1.5x + 1.2 is 1.5, which means that for every 1 unit increase in the number of assists, there is a corresponding 1.5 unit increase in the number of points.
b. To find the number of points for a player with 30 assists, we can substitute x = 30 into the model equation to get:
y = 1.5x + 1.2
= 1.5(30) + 1.2
= 45 + 1.2
= 46.2
Learn more about Scatter plot at:
brainly.com/question/6592115
#SPJ4
Ana works 25 hours a week at the library. If she is paid $10 an hour, and her net salary each week is $212.50, what percent of her salary is withheld for taxes?
Answers
Approximately 17.65% of Ana's salary is withheld for taxes.
To calculate the percentage of Ana's salary that is withheld for taxes, we need to determine the amount of tax withheld and then express it as a percentage of her net salary.
Number of hours worked per week (H) = 25 hours
Hourly wage (W) = $10
Net salary (S) = $212.50
Calculate the total earnings before taxes:
Total earnings = Hours worked * Hourly wage
Total earnings = 25 hours * $10/hour
Total earnings = $250
Determine the amount of tax withheld:
Tax withheld = Total earnings - Net salary
Tax withheld = $250 - $212.50
Tax withheld = $37.50
Calculate the percentage of salary withheld for taxes:
Percentage withheld = (Tax withheld / Net salary) * 100
Percentage withheld = ($37.50 / $212.50) * 100
Percentage withheld ≈ 17.65%
Therefore, approximately 17.65% of Ana's salary is withheld for taxes.
for such more question on percentage
https://brainly.com/question/24877689
#SPJ8
true or false? the dependent variable corresponds to the x-axis
Answers
Answer:
true
Step-by-step explanation:
im really not sure. it just sounds true
Answer:
false
Step-by-step explanation:
the x-axis is the indipendent variable
Please find the volume of the figure

Answers
The volume of the pyramid is 576 cubic inches.
To find the volume of a square base pyramid, you can use the formula:
Volume = (1/3) x base area x height
In this case, the side of the square base is given as 12 inches, and the height is given as 12.5 inches.
First, calculate the base area of the pyramid:
Base area = side²
= 12²
= 144 square inches
Now, substitute the values into the volume formula:
Volume = (1/3) x 144 x 12.5
Volume = 576 cubic inches
Therefore, the volume of the pyramid is 576 cubic inches.
Learn more about Volume here:
https://brainly.com/question/13338592
#SPJ1
In AGE and OLD, GAE - LOD, and AE = OD. To prove that AGE and OLD are congruent by SAS, what other information is needed?
Answers
For each triangle, identify a base and a corresponding height. Use them to find the area. Show your reasoning.
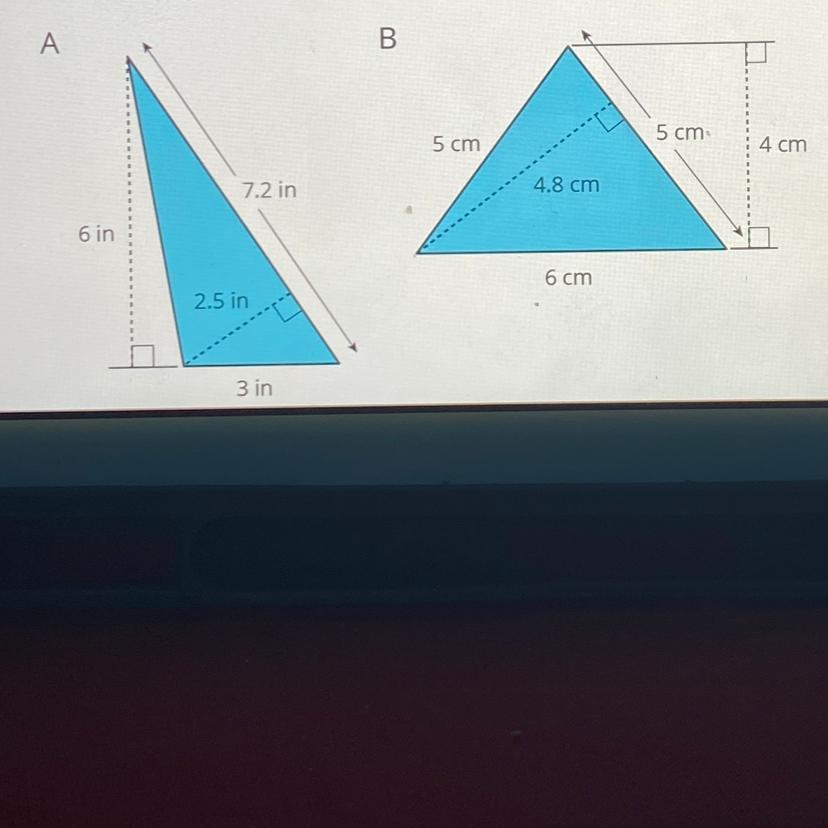
Answers
A. the identified base and corresponding height in figure A are 3 in. and 6 in. respectively.
The area is 9 sq. in.
B. the identified base and corresponding height in figure B are 6 cm and 4 cm in. respectively.
The area is 12 sq. cm
Recall:
The formula for area is given as: A = 1/2(base)(height)
The base of a triangle will be perpendicular to its height.
A. In the figure given in A, here, the dimensions are:
height = 6 inches
base = 3 inches
Area = 1/2(base)(height)
SubstituteArea = 1/2(3)(6)
Area = 9 sq. in.
B. In the figure given in B, here, the dimensions are:
height = 4 cm
base = 6 cm
Area = 1/2(base)(height)
SubstituteArea = 1/2(6)(4)
Area = 12 sq. cm
In summary,
A. the identified base and corresponding height in figure A are 3 in. and 6 in. respectively.
The area is 9 sq. in.
B. the identified base and corresponding height in figure B are 6 cm and 4 cm in. respectively.
The area is 12 sq. cm
Learn more here:
https://brainly.com/question/12932084
need help plz help for math class

Answers
-8/27
Step-by-step explanation:
Just multiply this fraction by itself 3 times and you will get the answer then simplify.
Please solve for brainliest.
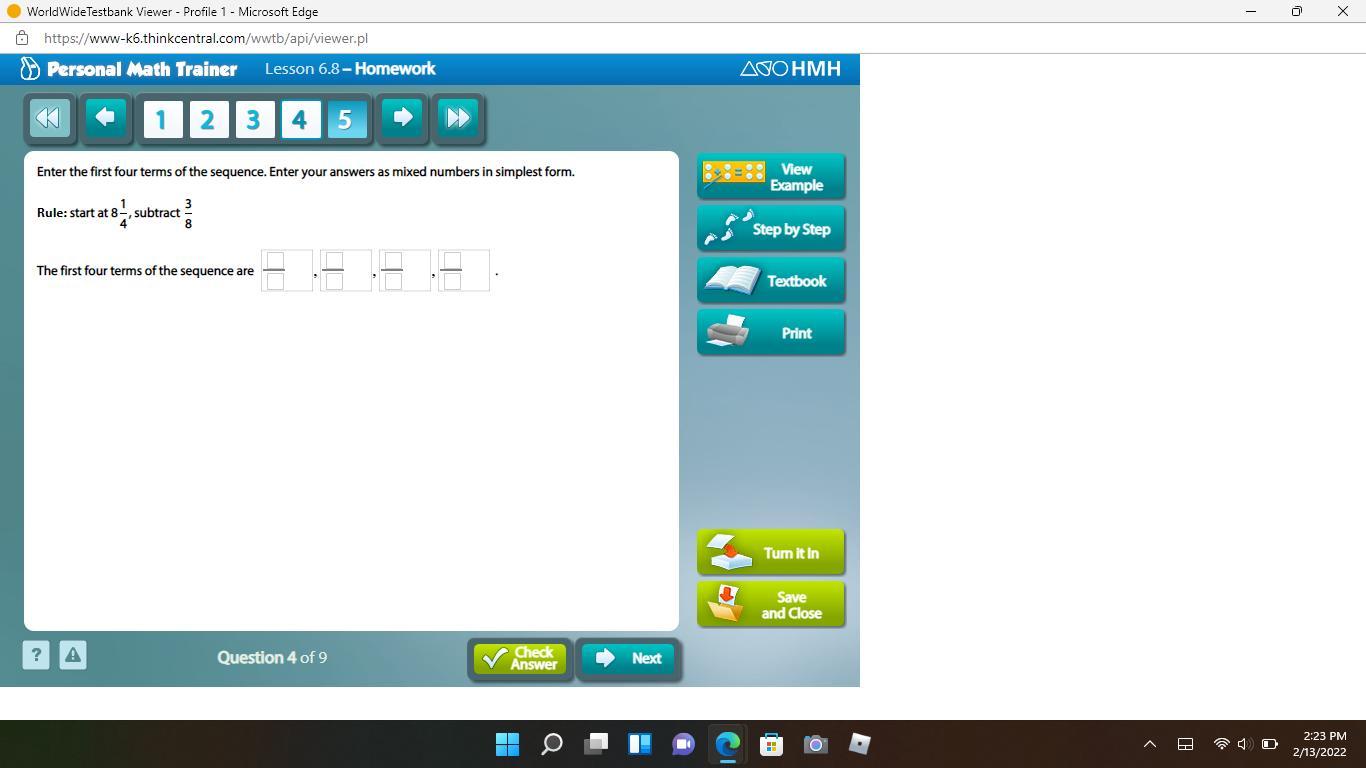
Answers
Answer: The first four terms are 33/4, 63/8, 15/2, and 57/8.
Step-by-step explanation: To make it easier, turn 8 1/4 into an improper fraction: 33/4. 33/4=66/8. Because the denominator is the same, it’s easier to subtract.
66/8 - 3/8 = 63/8
63/8 - 3/8 = 60/8
60/8 - 3/8 = 57/8
The first 4 terms in the sequence are 66/8, 63/8, 60/8, and 57/8. But we’re not done b/c we need to simplify. That means the first four terms are 33/4, 63/8, 15/2, and 57/8.
Analyze the diagram below and complete the instructions that follow.
42
40
A
Find the unknown side length, x. Write your answer in simplest radical form.
A. 2√√41
B. 4√√29
C. 48
D. 58
Mark this and return
Save and Exit
Next
Submit
Answers
The length of unknown side x is 58.
The correct answer is option D.
To find the unknown side length, x, in a right triangle with the base measuring 42 and the perpendicular measuring 40, we can use the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Let x be the hypotenuse. Applying the Pythagorean theorem, we have:
\(x^2 = 42^2 + 40^2\)
Simplifying:
\(x^2\) = 1764 + 1600
\(x^2\)= 3364
Taking the square root of both sides to solve for x:
x = \(\sqrt{3364}\)
Simplifying the square root:
x = (\(\sqrt{4 * 841)}\)
Since 841 is a perfect square (\(29^2\)), we can further simplify:
x = 2 * 29
x = 58
Therefore, the unknown side length, x, is equal to 58.
From the options provided the correct option is D.
For more such information on: length
https://brainly.com/question/28322552
#SPJ8
determine the value of x (asap)

Answers
The values of the missing terms are 1) 24 and 2) 1.6.
Given are two similar figures, we need to find the value of x,
According to the definition of similar figures, the ratios of the corresponding sides are equal,
So,
1) GE / EF = RS / TR
5/6 = 20/x
5x = 120
x = 24
2) JH / LK = WX / ZY
3.84 / 2.04 = 3.2 / x
3.84x = 2.04 × 3.2
3.84x = 6.528
x = 1.7
Hence, the values of the missing terms are 1) 24 and 2) 1.6.
Learn more about similar figures, click;
https://brainly.com/question/20368229
#SPJ1
schoepfle agency separates its accounts receivable into three age groups for purposes of estimating the percentage of uncollectible accounts. in addition, the balance of allowance for uncollectible accounts before adjustment is $12,500 (credit). accounts not yet due
Answers
a. total estimated uncollectible accounts is $21,190
b. to entry the adjustment, we have to debit bad debt expense and credit allowance for doubtful accounts in the amount of $14,690
a. to compute the estimated uncollectible accounts, we have to multiply the specific % to the accounts receivable plus the beginning balance;
•Accounts not due
$36,000 x 4% = $1,440
•Accounts 1 - 60 days past due
$21,000 x 25% = $5,250
•Accounts more than 60 days past due
$16,000 x 50% = $8,000
So the total uncollectible accounts would be; $6,500 + $1,440 + $5,250 + $8,000 = $21,190
b. to record the year-end adjustment of the uncollectible accounts, we have to debit bad debt expense and credit allowance for doubtful accounts in the amount of $14,690. This figure is the uncollectible amount we computed earlier based on the aging.
Therefore, the total estimated uncollectible accounts is $21,190 and to entry the adjustment, we have to debit bad debt expense and credit allowance for doubtful accounts in the amount of $14,690
To learn more about credit refer here
https://brainly.com/question/26867415
#SPJ4
Disclaimer
The question given by you is incomplete, so the above answer has been done as per a similar question
Spade Agency separates its accounts receivable into three age groups for purposes of estimating the percentage of uncollectible accounts. In addition, the balance of Allowance for Uncollectible Accounts before adjustment is $6,500 (credit).Accounts not yet due = $36,000; estimated uncollectible = 4%.Accounts 1–60 days past due = $21,000; estimated uncollectible = 25%.Accounts more than 60 days past due = $16,000; estimated uncollectible = 50%.Required:a. Compute the total estimated un-collectible accounts.b. Record the year-end adjustment for estmated un-collectable accounts.
The rectangular prisms below are filled with fractional unit cubes. Place the rectangular prisms in order from greatest volume to least volume.

Answers
Answer:
b - c - a
Step-by-step explanation:
Volume of each cube x number of cubes = total volume
a ) (3 * 2 * 6) * (1/4 )^3 = .5625
b) (2 * 3 ) * (1/2)^3 = .75
c) ( 8 * 4 * 11) * (1/8)^3 = .6875
The representation of the volume of the prism in greatest to least volume is third > first > second.
What is volume?Volume is the scalar quantity of any object that specified occupied space in 3D.
For example, the space in our room is referred to as volume.
As per the given cuboid prism.
The volume of the cuboid = length × height × width.
First cube = 1/4 x 3 x 6 x 2 = 9 units³
Second cube = 1/2 x 2 x 3 x 1 = 3 units³
Third cube = 1/8 x 8 x 11 x 4 = 44 units³
So, 44 > 9 > 3.
Hence "The representation of the volume of the prism in greatest to least volume is third > first > second".
To learn more about volume,
https://brainly.com/question/1578538
#SPJ2
if f(x)=2x^2-7 and g(x)=2x+1, evaluate f(g(x))
Answers
f(g(x))= 2(2x+1)^2-7
8x^2+8x-5

Simplify by writing without the absolute value sign.
|x-5| if x<5
Please help!
Answers
when x < 5, we can simplify it as -(x - 5) because (x - 5) is negative.
We have,
Absolute value:
The absolute value of a number represents its distance from zero on the number line. It is always a non-negative value.
For example, the absolute value of 3 is 3, and the absolute value of -3 is also 3.
|x - 5|:
In this expression, we have the absolute value of the quantity (x - 5).
It means that we are looking at the distance between x and 5 on the number line.
x < 5:
The condition x < 5 states that x is less than 5.
It means that x is located to the left of 5 on the number line.
Simplification:
When x is less than 5, it implies that x is located to the left of 5.
In this case,
The quantity (x - 5) becomes negative because we are subtracting a larger value (5) from a smaller value (x).
Now,
The expression |x - 5| can be simplified to -(x - 5), which means taking the negation of (x - 5).
- If x = 3, which is less than 5, we can substitute it into the expression:
|x - 5| = |3 - 5| = |-2| = 2
- If x = 7, which is greater than 5:
|x - 5| = |7 - 5| = |2| = 2
In both cases,
The value of |x - 5| is 2.
However, when x < 5, we can simplify it as -(x - 5) because (x - 5) is negative.
Thus,
when x < 5, we can simplify it as -(x - 5) because (x - 5) is negative.
Learn more about expression here:
https://brainly.com/question/20383699
#SPJ1
Complete each congruence statement by naming the corresponding angle or side (odd questions only)

Answers
Given:
1. \(\Delta HJI\cong \Delta IQP\)
3. \(\Delta JLK\cong \Delta FGH\)
To find:
The missing values to complete the congruence statements:
1. \(\overline{IH}\cong \_\_\_\_\)
3. \(\angle KJL\cong \_\_\_\_\_\)
Solution:
1.
We have,
\(\Delta HJI\cong \Delta IQP\)
Here, vertices H, J, I are corresponding to I, Q, P. So,
\(\overline{IH}\cong \overline{PI}\)
Therefore, the complete statement is \(\overline{IH}\cong \overline{PI}\).
3.
We have,
\(\Delta JLK\cong \Delta FGH\)
Here, vertices J, L, K are corresponding to F, G, H. So,
\(\angle KJL\cong \angle HFG\)
Therefore, the complete statement is \(\angle KJL\cong \angle HFG\).
What percent is represented by the shaded portion of this 10 × 10 grid? A grid model has 100 squares. 40 squares are shaded. StartFraction 4 Over 100 EndFraction percent StartFraction 40 Over 100 EndFraction percent 4% 40%
Answers
Answer:
40% \((\frac{40}{100})\)
Step-by-step explanation:
According to the given description of the 10 by 10 grid, 40 out of 100 squares are shaded.
Convert into a Fraction:
\(\frac{Shaded}{Squares} =\frac{40}{100}\)
Convert the fraction into a decimal:
\(\frac{40}{100} =0.4\)
Convert the decimal into a percent:
\(0.4*100=40\\\)
40%
So, the grid should represent 40%.
Answer:
40% got it right on the unit test.
Step-by-step explanation:
Which of the following statements is true regarding that equation |x+3|-2=k?

Answers
The true statement is if k = - 1 there are solutions, but if k = - 3 there are no solutions
How to determine which statement is true regarding the equation |x+3|-2=k?
Given: |x+3|-2=k
Below are rules for solving absolute value equations:
1. If p is positive and |y| = p, then
x = p OR y = -p
(two equations are set up)
2. If p is negative and |y| = p, then
No solution
3. If p is zero and |y| = p, then
One solution
Using the rules:
|x+3|-2=k
when k = -1
|x+3|-2= -1
|x+3| = 1
Rule 1 is applicable here. Thus, there are solutions
when k = -3
|x+3|-2 = -3
|x+3| = -1
Rule 3 is applicable here. Thus, no solution
Therefore, if k = - 1 there are solutions, but if k = - 3 there are no solutions. The 2nd option is the true statement
Learn more about absolute value equation on:
brainly.com/question/28728226
#SPJ1
what’s the correct radical form of b^1/5
Answers
The correct radical form of b^1/5 is 5^√b.
What is the radical form?Square root and nth roots are represented by the symbol "radical," which. a square root is a component of a radical expression, which is an expression.
A number's or an algebraic expression's simplest radical form is referred to as this. When a number or algebraic expression contains no elements that are perfect nth powers under the radical, it is said to have an nth root and is said to be in its simplest radical form.
When a number or algebraic expression contains no elements that are perfect nth powers under the radical, it is said to have an nth root and is said to be in its simplest radical form.
Explanation:
Convert to radical form using the formula
a^x/n=n^√a^x
5^√b.
To learn more about radical form refer to:
https://brainly.com/question/27887772
#SPJ1
solve for z
Z - 4/9 - 1/3 = 5/9
Answers
Answer:
4/3
Step-by-step explanation:
Z-4/9-1/3=5/9
Z-7/9=5/9
Z=5/9+7/9
Z=4/3 not sure
A case of single-serving bags of chips contains 8 boxes. Each box contains 10 bags of chips.
A case of chips cost $29.60. What is the unit price for a single bag of chips?
Answers
Answer:
each bag of chips are 0.37 cents
Step-by-step explanation:
1 case =29.60
29.60 divided by 8 (number of boxes in case)=3.70
3.70 divided by 10(number of chip bags in box)=0.37
Therefore each bag of chips = 0.37cents
solve for x
plss help

Answers
Answer:
2
Step-by-step explanation:
These two are similar triangles. 3 corresponds to 9, and x corresponds to 6. Since 3 is being multiplied by 3 to get 9, x*3 should equal 6. Therefore, x is 2.
If x is any real number, then x2 ≥ 1.
Select the correct answer.
x = -2.5
x = -1.5
x = 0.5
x = 1.5
Answers
Answer:
x≤−1 or x≥1
Step-by-step explanation:
