Suppose you have a bag of m&ms 4 green 6 yellow 7 purple 3 red. what is the probability you select a brown m&m
Answers
The probability of selecting a brown M&M from this bag is 0.
Since there are no brown M&Ms mentioned in your bag, the probability of selecting a brown M&M is 0. In probability terms, we can express this as:
Probability of selecting a brown M&M = Number of brown M&Ms / Total number of M&Ms
There are 0 brown M&Ms, and there are a total of 4 green + 6 yellow + 7 purple + 3 red = 20 M&Ms in the bag. So the probability is:
Probability = 0 / 20 = 0
Thus, the probability of selecting a brown M&M from this bag is 0, meaning it's impossible with the given information.
Learn more about probability,
https://brainly.com/question/24756209
#SPJ11
Related Questions
Evaluate f(-3), show all work:
F(x) = 2/3x + 8

Answers
Answer:
f(-3) = 6
Step-by-step explanation:
\(f(-3)=\frac{2}{3} (-3)+8=\frac{2(-3)}{3} +8=-\frac{6}{3}+8= -2+8=6\)
Hope this helps.
Answer:
f(x) = 6
Step-by-step explanation:
f(-3) means replace the x in f(x) with a -3, and replace every x in the equation with -3.
f(-3) = (2/3)x + 8
= (2/3) (-3) + 8
= (2 X -3)/3 + 8
= -6/3 + 8
= - 2 + 8
= 6
a factory was manufacturing products with a defective rate of 7.5%. if a customer purchases 3 of the products , what is the probability of getting at least one that is defective
Answers
If a customer purchases 3 of the products, the probability of getting at least one that is defective is 38.59%.
How to determine the probabilityIn order to determine the probability of getting at least one defective product if a customer purchases three products with a defective rate of 7.5%, we can use the concept of complementary probability.
The probability of getting at least one defective product can be calculated as the complement of the probability of getting none defective products.
So, the probability of getting no defective products is:
P(none defective) = (1 - 0.075)³ = 0.6141
Therefore, the probability of getting at least one defective product is:
P(at least one defective) = 1 - P(none defective) = 1 - 0.6141 = 0.3859 or 38.59%
.So, the probability of getting at least one that is defective is 38.59%.
Learn more about probability at
https://brainly.com/question/11234923
#SPJ11
If m∠AOD = (7x − 5)° and m∠BOC = (3x + 15)°, what is m∠BOC?
A. 5°
B. 30°
C. 39°
D.60°
Answers
To find the measure of angle BOC, set the expressions for m∠AOD and m∠BOC equal and solve for x. Then substitute the value of x back into the expression for m∠BOC to find its measure, which is 30°.
Explanation:To find the measure of angle BOC, we can set the expressions for m∠AOD and m∠BOC equal to each other and solve for x.
7x - 5 = 3x + 15
Subtract 3x from both sides: 4x - 5 = 15
Add 5 to both sides: 4x = 20
Divide both sides by 4: x = 5
Now that we know x = 5, we can substitute it back into the expression for m∠BOC to find its measure.
m∠BOC = (3x + 15)° = (3*5 + 15)° = 30°
Therefore, the measure of ∠BOC is 30°, which corresponds to option B.
Learn more about Angle Measurement here:
https://brainly.com/question/33833061
#SPJ2
Complete the table below by computing the gear ratios. Round to the nearest whole number.

Answers
By dividing the input gear's circumference by the output gear's circumference, we may determine the gear ratio between two gears .
what is ratio ?A mathematical comparison of two or more quantities that are somehow connected to one another is called a ratio. A colon or the phrase "to" might be used to denote the fractional part of the expression. Ratios can be employed in a variety of mathematical operations, including simplification, multiplication, and division by a common factor. They are frequently utilised in daily life, including in financial planning, sports statistics, and cooking recipes.
given
GearCombination DriverGearTeeth FollowerGearTeeth GearRatio
A-B 30 60 2
B-C 60 20 3
C-D 20 40 2
D-E 40 30 1
By dividing the input gear's circumference by the output gear's circumference, we may determine the gear ratio between two gears.
To know more about ratio visit:
https://brainly.com/question/29467965
#SPJ1
in the simplex method, the pivot column is the column with the most negative number (to the left of the vertical bar) in the bottom row. why?
Answers
The most negative number corresponds to the variable that has the largest impact on the Value of the objective function. So, maximizing it first is most efficient.
What is pivot column in simplex method?
The Simplex method's pivot column is selected by the fundamental variable's biggest reduced cost coefficient. 4. The highest ratio of right side parameters to positive coefficients in the pivot column determines the pivot row in the Simplex approach.
A location of a leading entry in the matrix's echelon structure. A pivot is a non-zero number that is either transformed into a leading 1 and then used to make 0s, or it is utilized in a pivot position to create 0s.
The element of a matrix or array chosen first by an algorithm (such as Gaussian elimination, simplex algorithm, etc.) to do particular computations is known as the pivot or pivot element.
To learn more about Simplex method's visit:https://brainly.com/question/15058261
#SPJ4
Plot the following equation in the complex Cartesian plane: 2Re(z) m(z 2 ) −3≥ Im(iz)
Answers
The equation to plot in the complex Cartesian plane is 2Re(z) - |z²| ≥ -3Im(iz).
To plot the equation 2Re(z) - |z²| ≥ -3Im(iz) graphically, you can follow these steps:
1. Represent the complex number z in terms of its real and imaginary parts, z = x + yi, where x is the real part and y is the imaginary part.
2. Substitute the values of x and y into the equation and simplify it.
3. Separate the equation into real and imaginary parts.
4. For each part, plot the corresponding inequality on the Cartesian plane.
- For the real part, plot the inequality 2x - |(x + yi)²| ≥ -3y.
- For the imaginary part, plot the inequality 0 ≥ 0 (as -3Im(iz) = 0 for all values of x and y).
5. Determine the common region that satisfies both inequalities. This region represents the solution to the original equation.
Learn more about complex number
https://brainly.com/question/20566728
#SPJ11
when solving a system of equations that includes one linear equation and one quadratic equation, how many solutions can be found?
Answers
A system of equations with one linear equation and one quadratic equation has "zero or one or two" solutions.
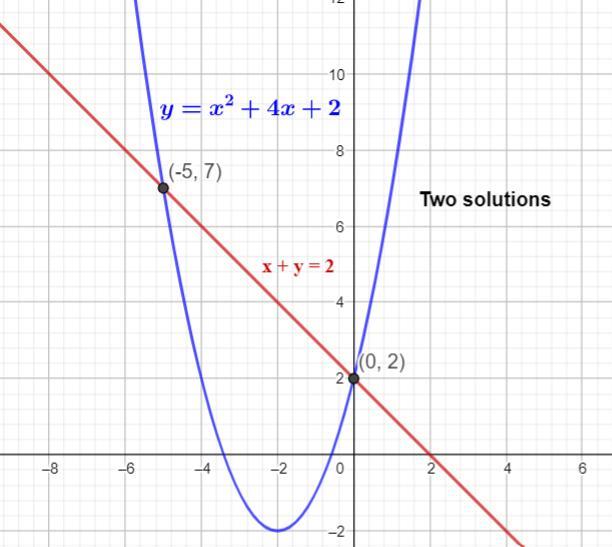
How to solve a system of equations that includes one linear equation and one quadratic equation?Consider a system of equations with one linear equation and one quadratic equation as
Case (1): y = x² + 4x + 2 ...(1)
and x + y = 2 ...(2)
By the substitution method:
from (2), y = 2 - x; Substituting in (1)
⇒ 2 - x = x² + 4x + 2
⇒ x² + 4x + 2 + x - 2 = 0
⇒ x² + 5x = 0
⇒ x(x + 5) = 0
∴ x = 0 and x = -5
If x = 0, then y = 2 - 0 = 2
If x = -5, then y = 2 + 5 = 7
So, the system has two solutions at (0, 2) and (-5, 7).
Case (2): y = x² + 4x + 2 ...(1)
and x - y = 2 ...(2)
By the substitution method:
from (2), y = x - 2; Substituting in (1)
⇒ x - 2 = x² + 4x + 2
⇒ x² + 4x + 2 + 2 - x = 0
⇒ x² + 3x + 4 = 0
we know that b² - 4ac will decide the nature of roots.
So, (3)² - 4(1)(4) = 9 - 16 = -7 < 0
Since the determinant is less than 0, the roots are imaginary. Hence the system has no solution. That means the line and the parabola do not meet.
Case (3): y = x² + 4x + 2 ...(1)
and y = x - 1/4 ...(2)
Substituting (2) in (1), we get
⇒ x - 1/4 = x² + 4x + 2
⇒ x² + 4x + 2 - x + 1/4 = 0
⇒ x² + 3x + 9/4 = 0
⇒ 4x² + 12x + 9 = 0
⇒ (2x + 3)² = 0
⇒ 2x + 3 = 0
∴ x = -3/2
If x = -3/2 then y = -3/4 - 1/4 = -7/4
So, the system has one solution at (-3/2, -7/4).
Therefore, the given type of system has "zero or one or two" solutions.
Learn more about the system of equations here:
https://brainly.com/question/2376175
#SPJ1


Evaluate the expression for x=4
3x^2

Answers
Answer:
Step-by-step explanation:
x = 4
3x^2
3(4)^2
3(16)= 48
Write -2.32 as a mixed number in simplest form.
Answers
Answer:
- 2 8/25
Step-by-step explanation:
Hope this helps! If it does, please mark me brainliest because it will help me. Thank you so much! ;) :)
Answer:
-2.32 as a mixed number is -2 32/100 = -2 8/25
Problem 7. What is the slope of tangent line to the curve f(x) = -3x2 - 6x at x = 1. a) m=0 b) f'x(x)=-6x-6 c) f'(x)=6x d) mz.12
Answers
The slope of the tangent line to the curve f(x) = -\(3x^2 - 6x\) at x = 1 is -12.
The correct option is d) mz.12
To find slope of the tangent line:
The slope of the tangent line to a curve at a specific point is given by the derivative of the function at that point.
In this case, the function is f(x) = \(-3x^2 - 6x\) and we want to find the slope of the tangent line at x = 1.
To do this,
we need to find the derivative of f(x) with respect to x, which is f'(x) = -6x - 6.
Then, we can evaluate this derivative at x = 1 to get the slope of the tangent line:
f'(1) = -6(1) - 6 = -12
Therefore, The slope of the tangent line to the curve f(x) = \(-3x^2 - 6x\) at x = 1 is -12.
The correct option is d) mz.12
To know more about Slope of the Tangent Line:
https://brainly.com/question/31326507
#SPJ11
Any genius willing to help :) , I'll give you a brainliest if you do.

Answers
Answer:
its in the shape of a tringle
Step-by-step explanation:
Answer:
See attached
Step-by-step explanation:
Definitely not a genius but I took a swing at it. I just plotted the points; I didn't connect anything.

Evaluate the expression when c = 5 and d = 8
d + 6c
Answers
Answer:
38
Step-by-step explanation:
6 times 5 =30
d=8
30+8-38
the area of a rectangle is equal to the area of a square with side 12cm if the breath of the rectangle is 8cm what is the length?
Answers
Side of the square is 12 cm. Area of the rectangle is equal to the area of the square and length of the rectangle is 16 cm. ∴ The required Perimeter of the rectangle is 50 cm.
what is the probability that the time until an accident occurs exceeds the mean time by more than 2 standard deviations?
Answers
The probability that the time until an accident occurs exceeds the mean time by more than 2 standard deviations is 0.0228 or 2.28%.
Using the standard normal distribution (Z) table.
Step 1: Convert the problem into a Z-score. In this case, the Z-score is 2 because we are looking for the probability of exceeding the mean by more than 2 standard deviations.
Step 2: Look up the Z-score of 2 in the standard normal distribution table. You will find a probability value of 0.9772. This value represents the probability that the time until an accident occurs is within 2 standard deviations from the mean.
Step 3: Since we are looking for the probability that the time exceeds the mean by more than 2 standard deviations, we need to find the probability of the complement. Subtract the probability found in Step 2 from 1.
1 - 0.9772 = 0.0228
So, the probability that the time until an accident occurs exceeds the mean time by more than 2 standard deviations is 0.0228 or 2.28%.
for such more question on probability
https://brainly.com/question/24756209
#SPJ11
I need help with this math question (pic induced)

Answers
Answer:
A
Step-by-step explanation:
Set the equation equal to bx.
\((3x + 3)(ax - 2) - {x}^{2} + 6 = bx\)
\(3a {x}^{2} - 6x + 3ax - 6 - {x}^{2} + 6 = bx\)
Cancel out the constants
\(3 {ax}^{2} - 6x + 3ax - x {}^{2} = bx\)
In order to cancel out the quadratics, we must solve for a.
\(3 {ax}^{2} - {x}^{2} = 0\)
\(3 {ax}^{2} = {x}^{2} \)
\(3a = 1\)
\(a = \frac{1}{3} \)
So plug in 1/3 for a.
\(3( \frac{1}{3} ) {x}^{2} - 6x + 3( \frac{1}{3} )x - {x}^{2} = bx\)
\( - 6x + x = bx\)
\( - 5x = bx\)
\(b = - 5\)
Find the area. Answer without units. *

Answers
The area of the composite figure composed of two rectangles is 217 centimetres squared
How to find the area of the composite figure?
The area of the composite figure can be found as follows:
The area of the composite figure can be found by adding up the individual area of each shape in the figure.
Therefore,
area of the figure = area of rectangle + area of rectangle
area of a rectangle = lw
where
l = lengthw = widthTherefore,
area of the figure = (14 × 11) + (7 × 9)
area of the figure = 154 + 63
area of the figure = 217 cm²
learn more on area here: https://brainly.com/question/14356835
#SPJ1
What is the discriminant of the quadratic equation 2x 5x² 1?
Answers
The Discriminant of the quadratic equation "2x + 5x² = 1" is 24 .
The Discriminant(D) of the Quadratic Equation ax² + bx + c can be calculated using the formula ; D = b² - 4ac .
the quadratic equation is given as 2x + 5x² = 1 ;
after rearranging the terms ,
the equation can be written as :
⇒ 5x² \(+\) 2x - 1 = 0 ;
Substituting the values in the discriminant formula ,
we get ;
D = (2)² - 4×5×(-1)
Simplifying further ,
we get ;
D = 4 + 20
D = 24 .
Therefore , the value of the Discriminant is 24 .
The given question is incomplete , the complete question is
What is the discriminant of the quadratic equation 2x + 5x² = 1 ?
Learn more about Discriminant here
https://brainly.com/question/7565929
#SPJ4
Helpppppppppppppppp

Answers
Answer:
when h(x) = 0, x = 7/3
Step-by-step explanation:
0 = 3x - 7
7 = 3x
7/3 = x
A bakery offers a sale price of 2.55 for 4 muffins.what is the price per dozen?
I hope someone answers fast
And explain what you did
Answers
Answer: $7.65 for a dozen/12
Step-by-step explanation: 2.55 x 3
190 people fit in 3 buses.
How many buses would you need to carry 570 people?
Answers
Answer:
9
Step-by-step explanation:
190 people=3 busses
570:190=3
so, 570 people= 190p. + 190p. +190p.= 3 busses +3 busses + 3 busses
Step-by-step explanation:
190 people = 3 busses
570:190=3
An orchard text design a rectangle flower garden such that the width is exactly 2/3 of length. 420 feet is antique picking fence are used to be enclosed the garden, find the dimension of the garden
Answers
A six-foot person walks from the base of a streetlight directly toward the tip of the shadow cast by the streetlight... (more down below)When the person is 12 feet from the streetlight and 5 feet from the tip of the streetlight's shadow, the person's shadow starts to appear beyond the streetlight's shadow.(a) Draw a right triangle that gives a visual representation of the problem. Show the known quantities and use a variable to indicate the height of the streetlight. (b) Use a trigonometric function to write an equation involving the unknown quantity.
h =(c) What is the height of the streetlight?
______ ft
Answers
b) h = \(tan \theta\) x 17 is the required equation.
c) The height of the streetlight is 20.4 ft.
The height of the person is 6 ft.
The distance at which the person is standing from the streetlight = 12 ft.
The distance at which the person's shadow appears = 5ft.
a) Hence, we can make the following diagram.
The right triangle below gives a visual representation of the problem. It shows the known quantities and a variable 'h' to indicate the height of the streetlight.
b) Let's now find an equation trigonometric function involving the unknown quantity 'h'.
from the below diagram, we can say that,
\(tan \theta\) = h/base
base= 12+5=17
hence we have, \(tan \theta\) = h/17
h = \(tan \theta\) x 17 is the required equation.
c) Now we have to find the height of the streetlight.
firstly let's find the value of \(\theta\),
\(\theta\) = tan 6/5.
\(tan^{-1}\)(6/5) = 50.2°
hence, tan 50.2 = h/17
1.20 = h/17
h= 1.20 x 17
h= 20.4 ft.
Hence, the height of the streetlight is 20.4 ft.
Read more about the trigonometric functions:
brainly.com/question/29492894
#SPJ4

DUE NOW PLEASE HELP!!!
Factor completely x2 − 10x + 25.
(x − 5)(x − 5)
(x + 5)(x + 5)
(x + 5)(x − 5)
(x − 25)(x − 1)
Answers
Answer:
(x - 5)(x - 5)
Step-by-step explanation:
\( {x}^{2} - 10x + 25 \: is \: the \: expansion \\ of \: {(x - 5)}^{2} \\ {(x - 5)}^{2} = (x - 5)(x - 5)\)
The complete factorization of the quadratic expression x² - 10x + 25 is (x - 5)(x - 5). Hence the first option is the right choice.
How to factor a quadratic expression?A quadratic expression of the form ax² + bx + c is factored by using the mid-term factorization method, which suggests that b should be broken in such two components that their product = ac. After this, we can factorize using the grouping method.
How to solve the given question?In the question, we are asked to factor the quadratic expression x² - 10x + 25 completely.
Comparing x² - 10x + 25 to ax² + bx + c, we get a = 1, b = -10, and c = 25.
To factor the expression we will use the mid-term factorization method, and try to break b in such two numbers whose product = ac.
Now, ac = 1 * 25 = 25. b = -10, which can be broken as -5, and -5.
Therefore, we can write the given expression as:
x² - 10x + 25
= x² - 5x - 5x + 25, mid-term factorization
= x(x - 5) -5(x - 5), grouping
= (x - 5)(x - 5), grouping.
Therefore, the complete factorization of the quadratic expression x² - 10x + 25 is (x - 5)(x - 5). Hence the first option is the right choice.
Learn more about mid-term factorization at
https://brainly.com/question/25829061
#SPJ2
what does 5 1/2 + 3 1/4 + 3 + 4 1/2 + 3 +3 2/5 equal also this is for Middle School not high school
Answers
Answer:
I think it's 22.65 but I'm not for sure
5) It is known that there is a linear relationship between
the cost of a taxi, C, in dollars and the distance travelled, d, in kilometres. This relationship can be represented by a straight line equation. When I travel 15km the taxi costs
me $32. 20 and when I travel 20km with the same company, the taxi costs
me $41. 70.
Develop algebraically, the linear equation, C = 1. 9 d + 3. 7, which
shows the relationship between the cost of the taxi, C, in terms of the
distance travelled, d
Answers
The linear equation that represents the relationship between the cost of a taxi, C, and the distance traveled, d, is C = 1.9d + 3.7. This equation shows that the cost of the taxi increases by 1.9 dollars for every kilometer traveled, with an additional fixed cost of 3.7 dollars.
To develop the linear equation, we need to consider the given information about the cost of the taxi for two different distances. When traveling 15km, the cost is $32.20, and when traveling 20km, the cost is $41.70. We can set up two equations based on this information:
32.20 = 1.9(15) + 3.7
41.70 = 1.9(20) + 3.7
Simplifying these equations, we get:
32.20 = 28.5 + 3.7
41.70 = 38 + 3.7
Solving these equations, we find:
32.20 = 32.20 (True)
41.70 = 41.70 (True)
Since both equations are true, we can conclude that the linear equation C = 1.9d + 3.7 accurately represents the relationship between the cost of the taxi, C, and the distance traveled, d. This means that for every kilometer traveled, the cost of the taxi increases by 1.9 dollars, and there is an additional fixed cost of 3.7 dollars.
Learn more about linear equation here:
https://brainly.com/question/12974594
#SPJ11
anyone knows the answer?!
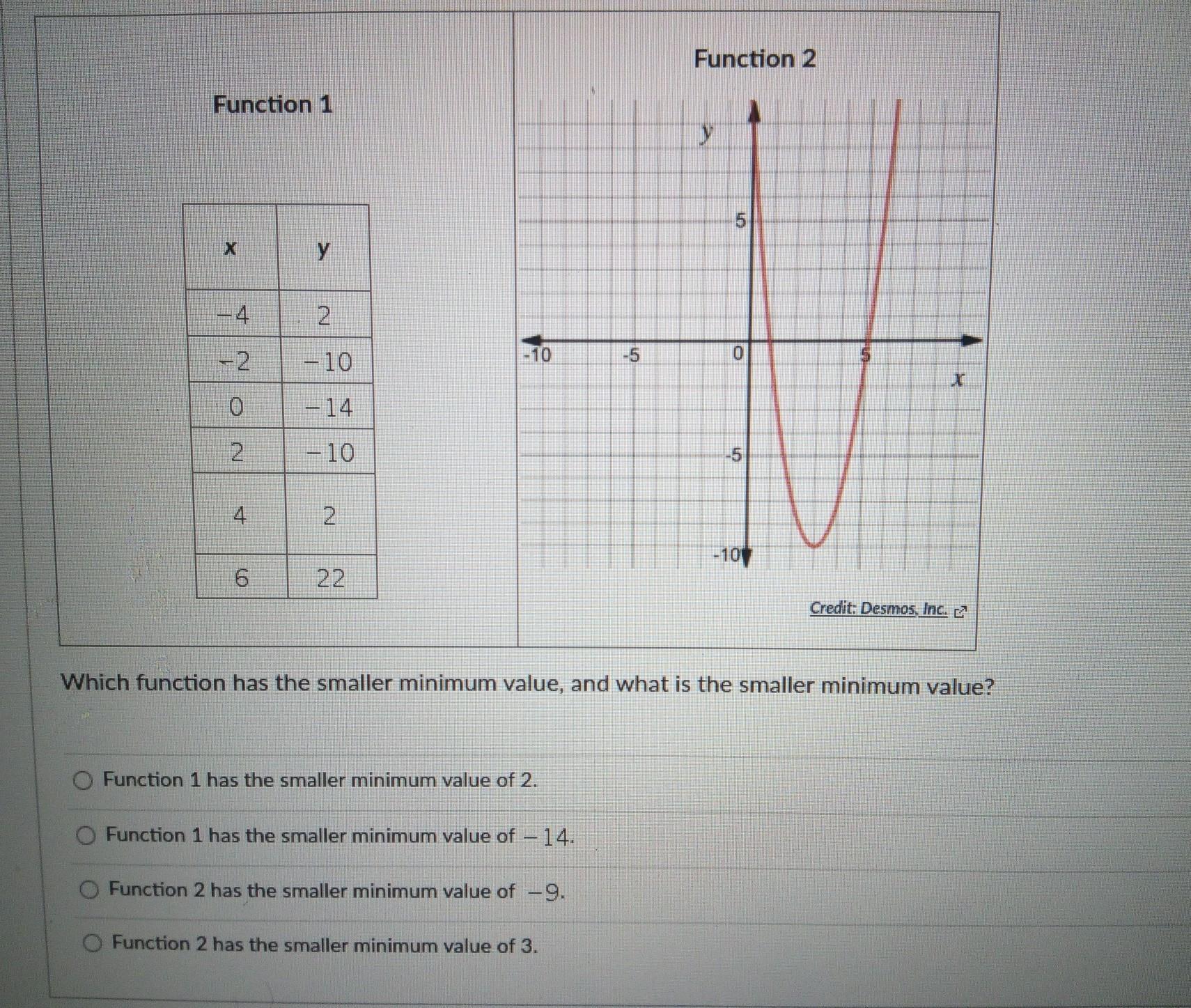
Answers
Answer:
Your answer is B) Function 1 has the smaller minimum value of -14.
Step-by-step explanation:
Method 1: Looking at the Function 1 and 2 points.
Method 2:
I have graphed functions 1 and 2 onto desmos to help determine which one has the smaller minimum.

Learn with an example
Does the point (2, 9) satisfy the inequality y > 3x + 3?
yes
no
Submit
Answers
Answer:
No
Step-by-step explanation:
When you plug in the numbers, you get:
9>6+3
9 is equal to 9, not greater than.
Evaluate the integral: (sec2(t) i + t(t2 + 1)4 j + t8 In(t) k) dt
Answers
The integral of (sec^2(t)i + t(t^2 + 1)^4j + t^8 ln(t)k) dt is equal to (tan(t)i + (t^7/7 + t^5/5 + t^3/3 + t)j + (t^9/9 ln(t) - t^9/81)k) + C, where C is the constant of integration.
To evaluate the given integral, we need to integrate each component of the vector separately. Let's consider each term one by one:
For the term sec^2(t)i, we know that the integral of sec^2(t) is equal to tan(t). Therefore, the integral of sec^2(t)i with respect to t is simply equal to tan(t)i.
For the term t(t^2 + 1)^4j, we can expand the term (t^2 + 1)^4 as (t^8 + 4t^6 + 6t^4 + 4t^2 + 1). Integrating each term individually, we obtain (t^9/9 + 4t^7/7 + 6t^5/5 + 4t^3/3 + t)j.
For the term t^8 ln(t)k, we integrate by parts, treating t^8 as the first function and ln(t) as the second function. Using the formula for integration by parts, we get (t^9/9 ln(t) - t^9/81)k.
Combining the results from each term, the integral of the given vector becomes (tan(t)i + (t^9/9 + 4t^7/7 + 6t^5/5 + 4t^3/3 + t)j + (t^9/9 ln(t) - t^9/81)k) + C, where C is the constant of integration.
Learn more about integral here:
https://brainly.com/question/31059545
#SPJ11
. The sum of the ages of x boys in a class is 84 years. When a new boy aged 8 years, 1 month joins the class, the average age is increased by 1 month
Answers
Answer:
The number of boys, x = 12
Step-by-step explanation:
Given that the sum of the ages of the boys in a class = 84 years
The number of boys = x
A new boy aged 8 years 1 month is added and the average age increases by 1 month
We have
Average age = 84/x = y
Age of new boy = 8 years 1 month = \(8\frac{1}{12} \ year\)
New average = y + 1/12 = \((8\frac{1}{12}+84) /(x + 1)\) which gives;
84/x + 1/12 = \((8\frac{1}{12} + 84) /(x + 1)\)
\(\dfrac{x +1008}{12 \cdot x} = \dfrac{1105}{12 \cdot x+ 12}\)
(x + 1008)×(12·x + 12) = 1105× 12·x
12·x² -1152·x + 12096 = 0
x² -96·x + 1008 = 0
(x - 84)×(x - 12) = 0
Therefore, x = 12 or 84,
The number of boys are 12 or 84
For there to bee 84 boys, their average age would be one year each
Given that they are boys not babies, then there are only 12 boys.
M is the centroid of the triangle.
CM=7, PM=10, & BQ=18
BM=[ ?]
Answers
Can I get a Brainly pls
![M is the centroid of the triangle.CM=7, PM=10, & BQ=18BM=[ ?]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/ln7s8vc9fb8N0T41xJdzq3bJP8hvPppt.png)