Suppose there is a 1.1 degree drop in temperature for every thousand feet that an airplane climbs into the sky. If the temperature o the ground is 59.7 degrees F, what will be the temperature at an altitude of 11,000 ft?
Answers
The temperature at an altitude of 11,000 ft is found to be 47.6 Degree Fahrenheit.
What is defined as the temperature?Temperature is a measure of how hot or cold something is demonstrated in terms of one of several scales, such as Fahrenheit and Celsius. Temperature signifies the direction wherein heat energy will instantaneously flow—that is, from a hotter (higher) body to a colder body (at a lower temperature).The plane is at ground level, with a temperature of 59.7 degrees Fahrenheit. The temperature drops by 1.1 degrees Fahrenheit for every 1,000 feet.
Initial Temp = 59.7 Fahrenheit
Distance Covered = 11,000 Ft
As the plane stands there, the ground level is zero feet.
Later, it soars into the sky at 11,000 feet.
= 11×1,000
Temperature drops by 1.1 degrees Fahrenheit for every 1,000.
As a result, at 11,000 feet, the temperature will drop 11 times,
= 11×1.1
or 12.1 degrees.
Therefore, at 11,000 feet, the temperature will be Fahrenheit,
= 59.7 - 12.1
= 47.6 degree Fahrenheit
Thus, the temperature at an altitude of 11,000 ft is computed as 47.6 degree Fahrenheit.
To know more about the temperature, here
https://brainly.com/question/25677592
#SPJ9
Related Questions
Your printer takes 36 seconds to print a small photo and 60 seconds to print a large one.
a.) Write an expression for the time (in seconds) your printer would take to print a batch
including both small and large photos.
b.) Find the time your printer would take to print 12 small photos and 5 large photos.
Answers
Answer: for part B = 732 seconds or 12.2 minutes
Step-by-step explanation: 36 seconds times the amount of small photos 12 = 432 plus 60 seconds times the amount of large 5 photos = 300 , 432 plus 300 equals 732 seconds
(36 x 12) + (60 x 5) = 732
After one quarter (year), the interest on a principal of $1000 is $8.75.
Find the rate. Write your answer as a percent.
Answers
\(~~~~~~ \textit{Simple Interest Earned} \\\\ I = Prt\qquad \begin{cases} I=\textit{interest earned}\dotfill & \$8.75\\ P=\textit{original amount deposited}\dotfill & \$1000\\ r=rate\to r\%\to \frac{r}{100}\\ t=years\dotfill &\frac{1}{4} \end{cases} \\\\\\ 8.75 = (1000)(\frac{r}{100})(\frac{1}{4})\implies 8.75=\cfrac{10r}{4} \\\\\\ 8.75=\cfrac{5r}{2}\implies 17.5=5r\implies \cfrac{17.5}{5}=r\implies \stackrel{\%}{3.5}=r\)
Walmart was having a sale on video games. They offered a 15% discount on a game that was originally priced at $30. After the sale, the discounted price of the game was increased by 10%. What is the new price of the game after this increase?
Answers
Answer:
28.05$
Step-by-step explanation:
The game got a discount of 15%.
New price is (30$) ( 0.85 ) = 25.5$ (since the discount is 15% you only pay for the 85% of the original price)
Then an increase of 10%. this is:
New price: 25.5$ (1.10) = 28.05
New price is 28$ with 5 cents
A class with n kids lines up for recess. The order in which the kids line up is random with each ordering being equally likely. There are two kids in the class named Betty and Mary. The use of the word "or" in the description of the events, should be interpreted as the inclusive or. That is "A or B" means that A is true, B is true, or both A and B are true.What is the probability that Betty is first in line or Mary is last in line as a function of n? Simplify your final expression as much as possible and include an explanation of how you calculated this probability.
Answers
The probability that Betty is first in line or Mary is last in line as a function of n is \(\frac{2n - 3}{n(n-1)}\).
It is given that number of kids are 'n' in the line including Betty and Mary. The total number of ways in which the kids can line up is "n!"
Let A denote that Betty is in the first place and B denotes that Marry is in the last place in the line.
Now, Betty can be at first place in (n-1)! ways
Therefore, P(A) = \(\frac{(n-1)!}{n!}\)
And Mary can be at last in the line in (n-1)! ways
Therefore, P(B) = \(\frac{(n-1)!}{n!}\)
Betty is first in the line and Mary is last in the line in (n-2)! ways
so P(A∩B) = \(\frac{ (n-2)! }{ n! }\)
The probability that Betty is first in line or Mary is last in line can be calculated by
P(A ∪ B) = P(A) + P(B) - P(A∩B)
P(A ∪ B) = \(\frac{(n-1)!}{n!}\) + \(\frac{(n-1)!}{n!}\) - \(\frac{ (n-2)! }{ n! }\)
P(A ∪ B) = \(\frac{1}{n} + \frac{1}{n} -\frac{1}{n(n-1)} =\frac{2n -3}{n(n-1)}\)
To learn more about Probability
https://brainly.com/question/13994656
#SPJ4
FactorsConsider the degree of each polynomial in theproblem.The first factor has a degree ofThe second factor has a degree ofThe third factor has a degree ofThe produa has a degree ofDONE

Answers
Given:
\((a^2)\left(2a^3\right)\lparen a^2-8a+9)\)To simplify:
Explanation:
Using polynomial multiplication,
\(\begin{gathered} (a^2)(2a^3)\operatorname{\lparen}a^2-8a+9)=2a^5\left(a^2-8a+9\right? \\ =2a^7-16a^6+18a^5 \end{gathered}\)Final answer:
\(\begin{equation*} 2a^7-16a^6+18a^5 \end{equation*}\)The degree of the polynomial is the largest power value of the variable.
Here the factors are,
\((a^2)(2a^3)\operatorname{\lparen}a^2-8a+9)\)So, we have,
The degree of the first factor is 2.
The degree of the second factor is 3.
The degree of the third factor is 2.
The product has a degree of 7.
WILL MARK BRAINLIEST PLEASE ANSWER 12/15+5/15 1 NUMBER FOR EACH SLOT

Answers
Answer:
17/15
Step-by-step explanation:
or if u reduce it would be 12/15
Gary applied the distributive property using the greatest common factor to determine the expression that is equivalent to 66 + 36. His work is shown below.
Factors of 66: 1, 2, 3, 6, 11, 22, 33, 66
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
66 + 36 = 3 (22 + 12)
What statement best describes Gary’s error?
Gary did not use correct factors for 66 in the equation.
Gary did not use correct factors for 36 in the equation.
Gary did not use two equivalent expressions in the equation.
Gary did not use the greatest common factor in the equation.
answer this question in 5 minutes and ill give you the brainlyest and 50 points also please still answer even after the 5 minutes
Answers
The statement which best describes Gary’s error is; Gary did not use the greatest common factor in the equation.
Greatest common factorThis is the largest positive integer or polynomial that is a divisor of several different numbers. For instance, the greatest common divisor of 66, 30 and 18 is 6.
Gary's work:
66 + 36
Factors of 66: 1, 2, 3, 6, 11, 22, 33, 66
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
66 + 36
= 3 (22 + 12)
Gary did not use the greatest common factor in the equation.
The correct answer:
The greatest common factor of 66 and 36 is 666 + 36
= 6(11 + 6)
Therefore, Gary did not use the greatest common factor in the equation.
Learn more about greatest common factor:
https://brainly.com/question/219464
#SPJ1
In a newspaper advertisement for a hybrid car, which of these presentation methods would be most effective?
Auto s
•
C chart showinq the rising price of gas
• a technical diagram of the hybrid engine and why it works
O a quote from a famous actress on why she bought a hybrid
•
a list of the most expensive gas stations in the city
Answers
What is the range of the function y=3√√x+8 1x

Answers
Answer:
The range of the function is: -∞≤y≤∞.
Consider the provided function.
The range of the function is the set of all values which a function can produce or the set of y values which a function can produce after substitute the possible values of x.
The range of a cubic root function is all real numbers.
Now consider the provided function.
The above function can be written as:
Taking cube on both sides.
The graph of the function is shown in figure 1:
For any value of x we can find different value of y.
Here, the cube root function can process negative values. Since, the function can produce any values, the range of the given function is -∞≤y≤∞ .
Therefore, the range of the function is: -∞≤y≤∞ (A).
10. The translation (x, y) (x + 10, y-6) is applied to AABC to create a new image AA'B'C'. Graph A’B’C’ on the coordinate plane
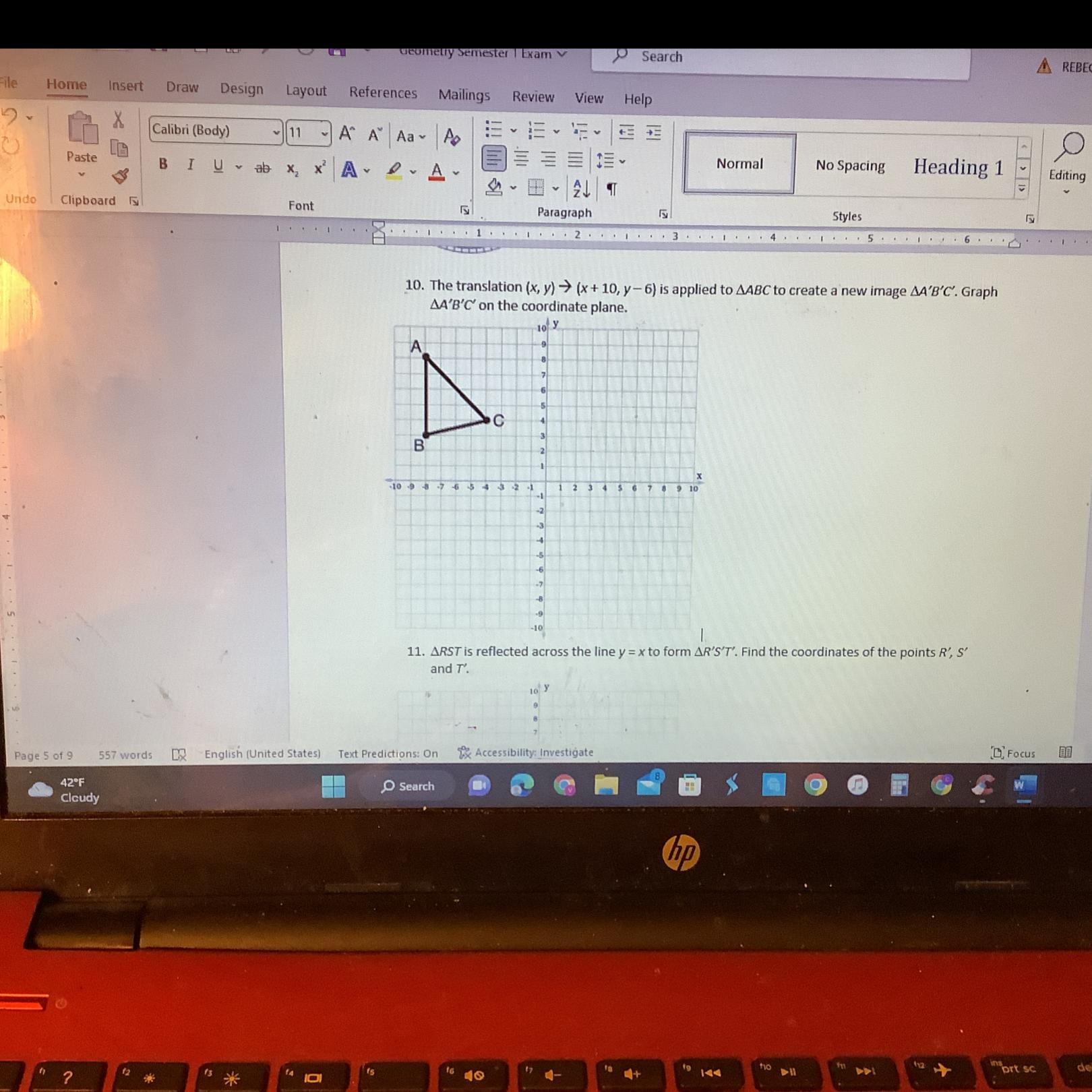
Answers
The image of the triangle ABC is shown in the image below attached.
How to generate the image of triangle by rigid translations
According to Euclidean geometry, triangles can be constructed by means of three non-colinear points. Two points are collinear when they can be contained by a line. The image of the triangle is the result of a rigid transformation known as translation:
P'(x, y) = P(x, y) + T(x, y)
Where:
P(x, y) - Original pointP'(x, y) - Image of the original point.T(x, y) - Translation vectorFirst, write the original points of the triangle:
A(x, y) = (- 8, 8), B(x, y) = (- 8, 3), C(x, y) = (- 4, 4)
Second, determine the image of each point:
A'(x, y) = (- 8, 8) + (10, - 6)
A'(x, y) = (2, 2)
B'(x, y) = (- 8, 3) + (10, - 6)
B'(x, y) = (2, - 3)
C'(x, y) = (- 4, 4) + (10, - 6)
C'(x, y) = (6, - 2)
Third, graph both the original and resulting triangle.
To learn more on rigid transformations: https://brainly.com/question/1761538
#SPJ1

The formula for the density of an object is d = m/v , where m is the mass and V is the
volume. Solve the formula for V in terms of d and m.
Answers
9514 1404 393
Answer:
v = m/d
Step-by-step explanation:
Multiply by v and divide by d.
d = m/v . . . . . given
vd = m . . . . . multiply by v
v = m/d . . . . . divide by d
_____
Additional comment
You can do both operations at once: multiply by v/d. This effectively switches the places of v and d in the given equation.
Answer:
dV
Step-by-step explanation:

please help with this question

Answers
The probability of the sample mean being less than 25.3 is given as follows:
0.9713 = 97.13%.
The sample mean would not be considered unusual, as it has a probability that is greater than 5%.
How to obtain probabilities using the normal distribution?The z-score of a measure X of a normally distributed variable that has mean represented by \(\mu\) and standard deviation represented by \(\sigma\) is obtained by the equation presented as follows:
\(Z = \frac{X - \mu}{\sigma}\)
The z-score represents how many standard deviations the measure X is above or below the mean of the distribution of the data-set, depending if the obtained z-score is positive(above the mean) or negative(below the mean).The z-score table is used to obtain the p-value of the z-score, and it represents the percentile of the measure X in the distribution.By the Central Limit Theorem, the sampling distribution of sample means of size n has standard deviation given by the equation presented as follows: \(s = \frac{\sigma}{\sqrt{n}}\).The parameters for this problem are given as follows:
\(\mu = 25, \sigma = 1.3, n = 68, s = \frac{1.3}{\sqrt{68}} = 0.1576\)
The probability of a score less than 25.3 is the p-value of Z when X = 25.3, hence:
Z = (25.3 - 25)/0.1576
Z = 1.9
Z = 1.9 has a p-value of 0.9713.
More can be learned about the normal distribution at https://brainly.com/question/25800303
#SPJ1
Use the diagram to find the angle measures
of the triangle. Recall that the sum of the
angle measures of a triangle is 180º.
9x
(x+4)
.
x =
(x+4)° = °
9x =

Answers
Answer:
x=16
(x+4)=20
9x=144
Step-by-step explanation:
9x+x+4+x=180
11x+4=180
11x=180-4
11x=176
\(x = \frac{176}{11} \)
x=16
Can I get help what does x equal?

Answers
Answer:
X is equal to 5
Step-by-step explanation:
If DE is a midsegment of the triangle, then segments AD and DB are congruent, therefore they have the same value.
solve ((-3) x (10 + (-7))) to the power of 2 divided by 3 - (-9) to the power of 2)
Answers
The solution of the given expression will be 9/16.
What is an expression?Expressions in maths are mathematical statements that have a minimum of two terms containing numbers or variables, or both, connected by an operator in between.
Given an expression, [-3*(10+(-7))]²÷[(3-(-9)]²
= [-3*(10+(-7))]²÷[(3-(-9)]² = (-9)²/12²
= 9/16
Hence, The solution of the given expression will be 9/16.
For more references on expression, click;
brainly.com/question/14083225
#SPJ1
write the expression 5x(x+9) -7(x+9) in complete factored form.
Answers
(5x-7)(x-9)
Step-by-step explanation:Factoring is the inverse of the distributive property. This means that we want to find the factors, not the product.
Partial Factoring
The expression we are given has already been factored to an extent. Both terms are split into 2 different factors. This was done by factoring out the greatest common factor (GCF) from both terms. In the first term, the GCF was 5x, and in the second, the GCF was -7.
Complete Factoring
Even though it was partially factored, we can factor it more. When given the situation:
a(x + y) - b(x + y)The expression can be factored into:
(a - b)(x + y)You can add (subtract in this case because 7 is negative) the values from outside the parentheses together. This term can then be multiplied by the value within the parentheses.
Thus, 5x(x+9) -7(x+9) can be factored into:
(5x-7)(x-9)Remember this trick only works when both terms share a factor like (x-9).
Please nswer this question.

Answers
Answer:
4.75 megabytes per second
Step-by-step explanation:
500-25 = 475
475 / 100 = 4.75
alternate exterior angles theorem
vertical angles theorem
corresponding angles postulate
same side interior angles theorem
alternate interior angles theorem
are all the second awsner which one is it
Whats the awnser Please Help

Answers
Answer:
x = 116
x° = 116°
(x - 52)° = 64°
Step-by-step explanation:
this shape is a right angle trapezoid and there are two 90° angles
the sum of all interior angles is 360°
90 + 90 + x + x - 52 = 360
2x - 52 = 180
2x = 232
x = 116
Seven subtracted from seven times a number is 147. What is the number?
Answers
Answer:
I answered your duplicate question. Make sure to check out the answer, and I hope it helps!
express(16^5)^1/4 in simplest radical form.
Answers
Answer:
32
Step-by-step explanation:
Hello, in (16^5)^1/4, you would multiply the exponents together like this:
16^5 x 1/4= 16^5/4
The exponents multiplied make 5/4. Now you need to multiply 16 with 5/4 like this:
16 x 5/4= 80/4
80 divided by 4 is 32 so therefore, the answer is 32.
a skeptical paranormal researcher claims that the proportion of americans that have seen a ufo, p, is less than 4 in every one thousand. assuming that a hypothesis test is conducted to test this claim, identify the null hypothesis h0 and the alternative hypothesis ha.
Answers
The null hypothesis h0 and the alternative hypothesis ha are,
Null hypothesis: \(p \leq 0.004\)
Alternative hypothesis: \(p > \frac{4}{1000} = 0.004\)
An alternative way to state the system of hypotheses is as follows:
Null hypothesis: \(p = 0.004\)
Alternative hypothesis: \(p > \frac{4}{1000} = 0.004\)
And that looks like the most logical alternative among the ones offered
C. H0: p = 0.004
H1: p > 0.004
Because the null hypothesis always requires an equal sign, and options A, B, and D do not meet this requirement.
The alternative hypothesis, which is what we are seeking to test in this experiment, is that "the proportion of Americans who have seen a UFO, p, is less than 4 in every 1,000" And thanks to the complement rule, the null hypothesis will exist.
This supports the following set of hypotheses:
Null hypothesis: \(p \leq 0.004\)
Alternative hypothesis: \(p > \frac{4}{1000} = 0.004\)
To read more about Hypothesis, visit https://brainly.com/question/16284715
#SPJ4
Dividing by a Monomial
What is (9x^3-6x^2+15x) ÷ 3x^2?
Answers
Answer:
\(3x-2+\frac{5}{x}\)
Step-by-step explanation:
To divide the polynomial (9x^3 - 6x^2 + 15x) by the monomial 3x^2, we can write it as:
(9x^3 - 6x^2 + 15x) ÷ (3x^2)
To simplify the division, we divide each term of the polynomial by 3x^2:
(9x^3 ÷ 3x^2) - (6x^2 ÷ 3x^2) + (15x ÷ 3x^2)
To divide monomials with the same base, we subtract the exponents. So:
9x^3 ÷ 3x^2 = 9/3 * (x^3/x^2) = 3x^(3-2) = 3x
(-6x^2) ÷ (3x^2) = -6/3 * (x^2/x^2) = -2
15x ÷ 3x^2 = 15/3 * (x/x^2) = 5/x
Putting it all together, we have:
(9x^3 - 6x^2 + 15x) ÷ (3x^2) = 3x - 2 + 5/x
Therefore, the division of (9x^3 - 6x^2 + 15x) by 3x^2 is 3x - 2 + 5/x.
Marlon is mixing blue paint and yellow paint in the ratio of 2:3 to make green paint. If he uses 8 liters of blue paint, how many liters of yellow paint will he need?
Answers
Answer:
12
Step-by-step explanation:
Evaluate the equation:
6w = 180
W = ____
Answers
Answer:
30
Step-by-step explanation:
Divide each term in 6 w = 180 by 6 and simplify. w = 30
Answer:
w = 30
Step-by-step explanation:
Given equation,
→ 6w = 180
Now the value of w will be,
→ 6w = 180
→ w = 180/6
→ [ w = 30 ]
Hence, the value of w is 30.
Find the surface area

Answers
Answer: 120 yds
Step-by-step explanation:
48+30+24+18+120 yds
The price-demand and cost functions for the production of microwaves are given as
p = 275 − x 60
p = 275 - x 60
and
C(x) = 50000 + 30x
where x is the number of microwaves that can be sold at a price of p dollars per unit and C(x) is the total cost (in dollars) of producing x
Required:
a. Find the profit function in terms of x.
b. Find the marginal cost as a function of x.
c. Find the revenue function in terms of x.
d. Find the marginal revenue function in terms of x.
Answers
Answer:
ALTERNATIVE 1
a. Find the profit function in terms of x.
P(x) = R(x) - C(x)
P(x) = (-60x² + 275x) - (50000 + 30x)
P(x) = -60x² + 245x - 50000
b. Find the marginal cost as a function of x.
C(x) = 50000 + 30x
C'(x) = 0 + 30 = 30
c. Find the revenue function in terms of x.
R(x) = x · p
R(x) = x · (275 - 60x)
R(x) = -60x² + 275x
d. Find the marginal revenue function in terms of x.
R'(x) = (-60 · 2x) + 275
R'(x) = -120x + 275
The answers do not make a lot of sense, specially the profit and marginal revenue functions. I believe that the question was not copied correctly and the price function should be p = 275 - x/60
ALTERNATIVE 2
a. Find the profit function in terms of x.
P(x) = R(x) - C(x)
P(x) = (-x²/60 + 275x) - (50000 + 30x)
P(x) = -x²/60 + 245x - 50000
b. Find the marginal cost as a function of x.
C(x) = 50000 + 30x
C'(x) = 0 + 30 = 30
c. Find the revenue function in terms of x.
R(x) = x · p
R(x) = x · (275 - x/60)
R(x) = -x²/60 + 275x
d. Find the marginal revenue function in terms of x.
R(x) = -x²/60 + 275x
R'(x) = -x/30 + 275
Figure ABCD is a parallelogram.
Parallelogram A B C D is shown. Angle B is (2 n + 15) degrees and angle D is (3 n minus 5) degrees.
Answers
A: ∠B = 55°; ∠D = 55°
Step-by-step explanation:
On Edg. 2021
Match each letter to its correct term. Efficiency Unobtainable Impossible Inefficiency Underutilization 1. A 2. B 3. C

Answers
Each letter should be matched to its correct term as follows;
1. A ⇔ Efficiency.
2. B ⇔ Impossible.
3. C ⇔ Inefficiency.
What is a production possibilities curve?In Economics and Mathematics, a production possibilities curve (PPC) can be defined as a type of graph that is typically used for illustrating the maximum and best combinations of two (2) products that can be produced by a producer (manufacturer) in an economy, if they both depend on the following two (2) factors;
Technology is fixed.Resources are fixed.Based on the production possibilities curve shown in the image attached above, we can reasonably infer and logically deduce that each of the letters represent the following terminologies;
A ⇔ Efficiency: it represent points on the production possibilities curve.B ⇔ Impossible: it represent points outside the production possibilities curve.C ⇔ Inefficiency: it represent points on the interior of a production possibilities curve.Read more on production possibilities here: brainly.com/question/26460726
#SPJ1

HELL PLZ! ITS SUPER EASY, ITS JUST 5 QUESTIONS AND IM IN 6TH GRADE MATH :)

Answers
Answer:
Step-by-step explanation:
Prime factorize
\(15) \sqrt{900}=\sqrt{3*3*2*2*5*5}=3*2*5=30\\\\\\16) \sqrt{1000000}=\sqrt{10*10*10*10*10*10}=10*10*10=1000\\\\17\sqrt{2*98}=\sqrt{2*2*7*7}=2*7=14\\\\18)\sqrt{37+84}=\sqrt{121}=\sqrt{11*11}=11\\\\19)24+\sqrt{3600}=24+\sqrt{6*6*10*10}=24+(6*10)=24+60=84\\\\20) \sqrt{\frac{560}{140}}=\sqrt{4}=2\\\\21)\sqrt{500-419}=\sqrt{81}=\sqrt{9*9}=9\)
\(22) \sqrt{6400}+37= \sqrt{8*8*10*10}+37=8*10 +37 = 80 + 37 = 117\\\\23)4\sqrt{81}=4*\sqrt{9*9}=4*9=36\\\\24)\sqrt{41+59}=\sqrt{100}=\sqrt{10*10}=10\\\\25)\sqrt{6400}=\sqrt{8*8*10*10}=8*10=80\\\\26)\sqrt{74-25}=\sqrt{49}=\sqrt{7*7}=7\)
The side of a triangle are in the ratio 4:4:3 what kind of triangle is it (b) calculate the smallest angle of the triangle to the nearest degree
Answers
The smallest angle of the equilateral triangle is 60 degrees
If the sides of a triangle are in the ratio 4:4:3, it implies that the lengths of the sides are proportional.
To determine the type of triangle, we examine the side lengths. Since all three sides are equal in length, we have an equilateral triangle.
For an equilateral triangle, all angles are equal. To calculate the smallest angle, we divide the total sum of angles in a triangle (180 degrees) by the number of angles, which is 3:
Smallest angle \(= \frac{180}{3} = 60\)\) degrees.
Therefore, the smallest angle of the equilateral triangle is 60 degrees (to the nearest degree).
For more questions on equilateral triangle:
https://brainly.com/question/17264112
#SPJ8