Suppose that E and Fare points on the number line. If EF=10 and E lies at - 17, where could F be located? If there is more than one location, separate them with commas.
Answers
Hence, on the number line, F may be at position -7.
What position does math's hold?
In mathematics, the term "position" refers to locating and noting the location of something, typically on a matrix or map. Typically, your youngster will use coordinates to complete this. Movement includes the ideas of symmetry, rotation, and translation. Geometry, the study of shapes, includes issues like position and motion.
Adding 10 to -17 will reveal the potential location(s) of F if E is located at -17 on the line segment and EF=10:
F = E + EF = -17 + 10 = -7
So, F could be located at -7 on the number line.
To know more about position visit:
https://brainly.com/question/28815991
#SPJ1
Related Questions
How would you write the expression "6 is less than a number tripled?"
Answers
Answer:
3q
Step-by-step explanation:
i think
Answer:
6< 3x
[where 3x = a number tripled]
write the equation of a circle given the center (2, 9) and radius r = 3
Answers
Answer: x^2 + y^2 - 4x + 18y = 76 = 0
The center of the circle given is (2, 9)
radius = r
The equation of a circle for a given point is
(x - h)^2 + (y - k)^2 = r^2
Where h = 2, and y = 9
(x - 2)^2 + (y - 9)^2 = 3^2
Expand the parentheses
(x - 2) (x - 2) + (y - 9) (y - 9) = 9
(x - 2) (x - 2 ) = x* x - 2*x - 2*x + 2* 2
= x^2 - 4x + 4
(x - 2) (x - 2) = x^2 - 4x + 4
(y - 9) (y - 9) = y*y - y*9 - 9*y + 9*9
= y^2 - 18y + 81
(y - 9) (y - 9)= y^2 - 18y + 81
Therefore, the equation becomes
x^2 - 4x + 4 + y^2 - 18y + 81 = 9
Re-arrange the equation
x^2 + y^2 - 4x - 18y + 4 + 81 = 9
x^2 + y^2 - 4x - 18y = 9 - 81 - 4
x^2 + y^2 - 4x - 18y = -76
x^2 + y^2 - 4x - 18y + 76 = 0
The equation of a circle given the center (2, 9) and radius 3 is x^2 + y^2 - 4x + 18y = 76 = 0
Answer:
The equation of a circle given the center (2, 9) and radius 3 is x^2 + y^2 - 4x + 18y = 76 = 0
Step-by-step explanation:
Constant Variance Definition
Answers
Constant variance, also known as homoscedasticity, is a statistical property where the variance of a variable is equal across all values of the variable.
This means that the variability of the variable is consistent, no matter what the value of the variable is. Mathematically, this is expressed by the formula:
Var(X) = σ^2
where Var(X) is the variance of the variable X, and σ^2 is the same across all values of X.
For example, if we look at the heights of a group of people, we may find that the variance of their heights is equal to 25 cm, no matter what the heights are. In this case, the variance of the heights is 25 cm, and this variance (25 cm) is the same for all the heights in the group.
Learn more about Constant variance here :
https://brainly.com/question/29644611
#SPJ4
Wanda wants to buy a pair of shoes that cost $48 if sales tax is 8.25% what will be the total cost
Answers
Now add 3.96 + 48
Answer 51.96
Help me geometry 7th grade

Answers
We know 7 becomes 3.5, which means the second rectangle is half the size of the first one (because 7 divided by 2 is 3.5)
Therefore, to find the missing measure, or x cm, you have to divide 4 by 2, which is 2
Therefore, x=2
Two numbers have a difference of -72 and a product of -720? What is their sum?
Answers
The answer to the question "difference of -72 and a product of -720?" is -9.
What is the sum of two numbers with a difference of -72 and a product of -720?To find the sum of the two numbers, we can set up the following equations based on the given information:
Let the two numbers be x and y, where x > y.
x - y = -72 (since the difference between the numbers is -72)
xy = -720 (since the product of the numbers is -720)
We can solve these equations simultaneously using algebraic methods. One way to do this is to isolate one of the variables in one of the equations and substitute it into the other equation. For example, we can isolate y in the first equation by rearranging it to y = x + 72, and then substitute this into the second equation:
x(x + 72) = -720
Expanding the left-hand side, we get:
x^2 + 72x = -720
Rearranging the equation, we get:
x^2 + 72x + 720 = 0
Now we can solve for x using the quadratic formula:
x = (-b ± √(b^2 - 4ac)) / (2a)
where a = 1, b = 72, and c = 720. Plugging in these values, we get:
x = (-72 ± √(72^2 - 4(1)(720))) / (2(1))
Simplifying further, we get:
x = (-72 ± √(5184 - 2880)) / 2
x = (-72 ± √2304) / 2
x = (-72 ± 48) / 2
Now we have two possible values for x:
x1 = (-72 + 48) / 2 = -12
x2 = (-72 - 48) / 2 = -60
Since x > y, we take x = -12 and y = -72 - (-12) = -60 + 12 = -48.
Thus, the sum of the two numbers is -9, which is obtained by adding x and y:
-12 + (-48) = -9.
Read more about sum of number
brainly.com/question/5982761
#SPJ1
Fiona is driving through the twin at a rate of 30 feet per second . Which graph could represent the relationship between the time , in seconds , and the distance , in feet, that Fiona drives through town
If you hurry I’ll mark you brainliest

Answers
Answer:
B
Step-by-step explanation:
B] The rate of feet per a second is 30 therefore it is B.
The table shows the number of points scored by a basketball team in their first seven games.

Answers
Answer:
15
Step-by-step explanation:
the range is the largest number take away the smallest number
56-41=15
Please help if you can :)
(98 ÷ 14 + x - 9/ 24) × 40 = 480
(the slash is a fraction of x-9 over 24)
Answers
hi! im chimken and i have your answers!
x = 43/8
( 98 ÷ 14 + x - 9 / 24 ) • 40 = 480
( 7 + x - 9 / 24 ) • 40 = 480
( 53 / 8 + x ) • 40 = 480
265 + 40x = 480
40x = 480 - 265
40x = 215
x = 43 / 8
i hope this helped! have a good day! :)
praise bingus!
Answer: x = 43/8
HOPE THIS HELPS
How do you answer this question?:
5x^2+14x=x+6
Answers
The solutions to the equation 5x²+14x=x+6 are x = 4/5 or x = -3 we solved by using quadratic formula
The given equation is 5x²+14x=x+6
We have to solve for x
Subtract x from both sides
5x²+13x=6
Subtract 6 from both sides
5x²+13x-6=0
Now we can use the quadratic formula to solve for x:
x = (-b ± √(b²- 4ac)) / 2a
where a = 5, b = 13, and c = -6.
Substituting these values and simplifying:
x = (-13 ±√(13²- 4(5)(-6))) / (2 × 5)
x = (-13 ± √289)) / 10
x = (-13 ± 17) / 10
So we get two solutions:
x = 4/5 or x = -3
Therefore, the solutions to the equation 5x^2 + 14x = x + 6 are x = 4/5 or x = -3.
To learn more on Quadratic equation click:
https://brainly.com/question/17177510
#SPJ1
whats the hypotenuse of this triangle?
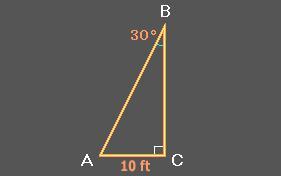
Answers
Using trigonometric ratio, the hypothenuse is 20ft
What is trigonometric ratio?
Trigonometric ratios, also known as trigonometric functions or trig functions, are mathematical functions that relate the angles of a right triangle to the ratios of the sides of the triangle. The most common trigonometric ratios are: sine, cosine and tangent.
In this question given;
We have the angle and the opposite of the angle;
opposite = 10ftangle = 30°Using the sine ratio;
sin 30 = opposite / hypothenuse
sin 30 = 10 / x
cross multiply both sides and solve for x;
x = 10/sin30
x = 10 / 0.5
x = 20ft
The hypothenuse is 20ft
Learn more on trigonometric ratio here;
https://brainly.com/question/17155803
#SPJ1
find the x and y intercepts of the line calculator
Answers
The x-intercept of the line calculator is (-1,0) while the y-intercept is (0,-3).
To determine the x-intercept, let y = 0 and solve for x in the equation y = 3x - 1.
Substitute 0 for y in the equation.0 = 3x - 1
Add 1 to both sides1 = 3x
Divide both sides by 3x = 1/3
The x-intercept of the line is (1/3, 0).
To find the y-intercept, let x = 0 and solve for y in the equation y = 3x - 1.
Substitute 0 for x in the equation.y = 3(0) - 1y = -1
The y-intercept of the line is (0, -1).
Therefore, the x-intercept is (1/3, 0), and the y-intercept is (0, -1).
Therefore, The x-intercept of the line calculator is (-1,0) while the y-intercept is (0,-3). The calculation above supports the conclusion.
To know more about, line calculator, visit
https://brainly.com/question/30763905
#SPJ11
A triangle has sides with lengths of 5 kilometers, 11 kilometers, and 12 kilometers. Is it a right triangle?
Answers
Answer:
Step-by-step explanation:
to prove it right angle
square of largst side must be eqaul to the sum of two other sides.
so here 12 is largest and 11 and 5 are two other smallest sides of a triangle.
(12)^2=(11)^2+(5)^2
144=121+25
144=146
since the square of largest side is not equal to the sum of square of other two smaller sides it can be concluded that the given sides of a triangle does not form a right angled triangle.
Jadon has 4 feet of ribbon to decorate pockets. He needs 1/3 foot of ribbon to decorate each pocket. How many pockets will jadon be able to decorate?.
Answers
Answer:
4 feet of ribbon ÷ 1/3 foot riboon = 12 pockets
The graph of y= f(x) is shown below. Find all values of x where f (x) =0.

Answers
The values of x when the graph of f(x) = 0 are 8
How to determine the values of x when f(x) = 0?From the question, we have the a graph that can be used in our computation:
This means the graph represents the given parameter
To calculate the values of x when f(x) = 0, we simply determine the x-coordinate when the line of the graph cross the x-axis
In this case, the x-coordinate is
x = 8
Note that this represents the x-intercept
Read more about intercepts at
brainly.com/question/20687801
#SPJ1
The total number of data items with a value less than the upper limit for the class is given by the _____ distribution.
Answers
The cumulative frequency distribution indicates the total number of data items with values below the class's upper limit.
By cumulative frequency, what do you mean?Cumulative frequency analysis examines how frequently values of a phenomena occur that are less frequent than a reference value. The phenomenon could depend on time or place. Another name for cumulative frequency is frequency of non-exceedance. Each frequency from a frequency distribution table is added to the total of its predecessors to determine the cumulative frequency. Since all frequencies will have previously been added to the prior total, the final result will always be equal to the sum of all observations. The quantity of an element in a set is referred to as the element's frequency. The accumulation of all earlier frequencies up to the present time is another definition for cumulative frequency.
To know more about Cumulative frequency , click here:
https://brainly.com/question/5102661
#SPJ4
somebody please help me with this question and no links!

Answers
Answer:
x = 14°
Step-by-step explanation:
4x + 2x + 6 = 90
6x + 6 = 90
subtract 6 from both sides
6x = 84
divide by 6 on both sides
x = 14°
If my answer is incorrect, pls correct me!
If you like my answer and explanation, mark me as brainliest!
-Chetan K
Given the graph and the equation y = 2x2 - 8x + 3. which one has the smaller minimum and by how much?
A)
The graph by 6 units
B)
The graph by 70 units
C)
The equation by 2 units
D)
The equation by 5 units
Answers
Answer:
c
Step-by-step explanation:
y=2(2)2-8(2)+3
=8-16+3
=-8+3
=-5
Answer:
c
Step-by-step explanation:
i did the prep
Simplify the algebraic expression: 4n + 19 + 3n - 2n - 5 A. 19n B. 33n C. 5n + 14 D. 9n + 24
Answers
\(\huge\text{Hey there!}\)
\(\large\text{4n + 19 + 3n - 2n - 5}\)
\(\large\text{COMBINE the LIKE TERMS}\)
\(\large\text{(4n + 3n - 2n) + (19 - 5)}\)
\(\large\text{4n + 3n - 2n}\\\large\text{4n + 3n = \bf 7n}\\\large\text{7n - 2n = \bf 5n}\)
\(\large\text{5n + (19 - 5)}\)
\(\large\text{19 - 5 = \bf 14}\)
\(\large\text{= \bf 5n + 14}\)
\(\boxed{\boxed{\large\textsf{Answer: \huge \bf Option C. 5n + 14}}}\huge\checkmark\)
\(\text{Good luck on your assignment and enjoy your day!}\)
~\(\frak{Amphitrite1040:)}\)
Branily should call brainliest “smartiest”
Anyway please do this question it might be the last one for slopes

Answers
The slope is -20/27 :)
Answer:
- 20 / 27
Step-by-step explanation:
( x1, y1 ) = ( 28, 51 )
Here,
x1 = 28
y1 = 51
( x2, y2 ) = ( - 26, 91 )
Here,
x2 = - 26
y2 = 91
Formula : -
Slope = ( y2 - y1 ) / ( x2 - x1 )
Slope = ( 91 - 51 ) / ( - 26 - 28 )
= 40 / - 54
= - 40 / 54
Slope = - 20 / 27
Proper fraction = - 20 / 27
How do you graph piecewise functions on Desmos?
Answers
A piecewise function is a function that is defined by different equations on different intervals.
Graphing a piecewise function on a graph is a great way to visualize its behavior and understand its properties. One of the most popular and user-friendly ways to graph piecewise functions is using the online graphing calculator Desmos.
Here is a step-by-step guide on how to graph a piecewise function on Desmos:
Go to the Desmos website
and click on the "Graphing Calculator" button.
On the left side of the screen, you will see a text box labeled "y=". This is where you will enter the equation of your piecewise function. You can enter multiple equations by separating them with commas.
To graph a piecewise function, you will need to enter different equations for different intervals.
For example, if you have a piecewise function that is defined by the equation y = x^2 for x < 0 and y = x + 2 for x ≥ 0, you would enter y = x^2, x < 0 and y = x + 2, x ≥ 0 in the "y=" text box.
Once you have entered your equations, press the "Graph" button to see the graph of your piecewise function on the screen.
If you want to adjust the graph, you can use the sliders on the left side of the screen to change the range of the x- and y-axis. You can also use the buttons at the top of the screen to zoom in and out or pan around the graph.
To see the graph of multiple piecewise functions at once you can use the "Add another equation" button under the "y=" text box to add additional equations.
You can also use the "Table" tab to see the values of the function at certain x-values and also can use the "Slider" tab to change the value of x and see how that effects the graph of the function.
By following these steps, you can easily graph piecewise functions on Desmos and visualize the behavior of the function. Desmos is a great tool that allows you to experiment with different equations and see how they affect the graph of the function.
It is a great way to understand the properties of piecewise functions and to visualize them in multiple ways.
to know more about graph refer here
https://brainly.com/question/17267403#
#SPJ11
jeff lives 12 miles east of stan jeff lives 16 miles north of wei what is the shortest stan and wei can live from each other
Answers
Answer:
20 miles
Step-by-step explanation:
first, draw a diagram. Then, use the pythagorean theorem to calculate.
the angle of elevation from a rowboat moored 75 feet from a cliff is 73.8 degrees.find the height of the cliff to the nearest foot.
Answers
The height of the cliff is approximately 269 feet.
We will be using the tangent function to find the height of the cliff.
Draw a right triangle with the rowboat at one corner, the cliff's base as the adjacent side, and the cliff's height as the opposite side.
The angle of elevation (73.8 degrees) is between the rowboat and the cliff's base.
We are given the adjacent side (75 feet) and we need to find the opposite side (height of the cliff).
To do this, we will use the tangent function:
tan(angle) = opposite side / adjacent side
Plug in the given values:
tan(73.8) = height / 75
Solve for the height:
height = tan(73.8) * 75
Calculate the value:
height ≈ 269.4 feet
Round the height to the nearest foot:
height ≈ 269 feet.
For similar question on function.
https://brainly.com/question/24748644
#SPJ11
Assuming that someone is asked to write a code (i.e., program) for nonlinear problem using least square adjustment technique, what would be your advice for this person to terminate the program?
Answers
This criterion can be defined based on the desired level of accuracy or when the change in the estimated parameters falls below a certain threshold.
When implementing a program for a nonlinear problem using the least square adjustment technique, it is essential to determine a termination condition. This condition dictates when the program should stop iterating and provide the final estimated parameters. A common approach is to set a convergence criterion, which measures the change in the estimated parameters between iterations.
One possible criterion is to check if the change in the estimated parameters falls below a predetermined threshold. This implies that the adjustment process has reached a point where further iterations yield minimal improvements. The threshold value can be defined based on the desired level of accuracy or the specific requirements of the problem at hand.
Alternatively, convergence can also be determined based on the objective function. If the objective function decreases below a certain tolerance or stabilizes within a defined range, it can indicate that the solution has converged.
Considering the chosen termination condition is crucial to ensure that the program terminates effectively and efficiently, providing reliable results for the nonlinear problem.
Learn more about nonlinear problem: brainly.com/question/31457669
#SPJ11
(1) Determine the convergence of the series ∑[infinity]
n=1
(−1)n
4n.
(2) Determine the convergence of the series ∑[infinity]
n=1
n(−1)n
3.5n.
Answers
Both conditions are satisfied. Therefore, the series \(\sum_{n=1}^{\infty} \frac{(-1)^n}{4n}\) converges. The series \(\sum_{n=1}^{\infty} n \cdot (-1)^n \cdot \left(\frac{1}{3.5}\right)^n\) converges absolutely.
To determine the convergence of a series, we can apply various convergence tests. Let's analyze each series separately:
1. \(\sum_{n=1}^{\infty} \frac{(-1)^n}{4n}\)
This series is an alternating series since it alternates between positive and negative terms. To determine its convergence, we can use the Alternating Series Test. The Alternating Series Test states that if a series of the form \(\sum_{n=1}^{\infty} (-1)^{n-1} \cdot b_n\) satisfies the following conditions:
1. The terms \(b_n\) are positive and decreasing for all n.
2. The limit of \(b_n\) as n approaches infinity is zero.
In our case, \(b_n = 1/(4n)\). Let's check the conditions:
Condition 1: The terms \(b_n = 1/(4n)\) are positive for all n.
Condition 2: Let's calculate the limit of b_n as n approaches infinity:
\(\lim_{{n \to \infty}} \left(\frac{1}{{4n}}\right) = 0\)
Both conditions are satisfied. Therefore, the series \(\sum_{n=1}^{\infty} \frac{(-1)^n}{4n}\) converges.
2. \(\sum_{n=1}^{\infty} n \cdot (-1)^n \cdot \left(\frac{1}{3.5}\right)^n\)
To determine the convergence of this series, we can use the Ratio Test. The Ratio Test states that for a series \(\sum_{n=1}^{\infty} a_n\) , if the following limit exists:
\(\lim_{{n \to \infty}} \left| \frac{{a_{n+1}}}{{a_n}} \right| = L\)
1. If L < 1, the series converges absolutely.
2. If L > 1, the series diverges.
3. If L = 1, the test is inconclusive.
In our case, \(a_n = \frac{n \cdot (-1)^n}{3.5^n}\) . Let's apply the Ratio Test:
\(\left| \frac{{(n+1) \cdot (-1)^{n+1}}}{{3.5^{n+1}}} \div \frac{{n \cdot (-1)^n}}{{3.5^n}} \right|\)
\(\left| \frac{{(n+1)/n \cdot (-1)^2}}{{3.5}} \right|\)
\(\left| \frac{{n+1}}{{n}} \right| \cdot \frac{1}{3.5}\)
\(\frac{{n+1}}{{n}} \cdot \frac{1}{3.5}\)
Taking the limit as n approaches infinity:
\(\lim_{{n\to\infty}} \left(\frac{{n+1}}{n} \cdot \frac{1}{3.5}\right) = \frac{1}{3.5}\)
Since 1/3.5 < 1, the series \(\sum_{n=1}^{\infty} n \cdot (-1)^n \cdot \left(\frac{1}{3.5}\right)^n\) converges absolutely.
Therefore, both series converge.
To learn more about series ,
https://brainly.com/question/30087275
#SPJ4
Mr. Johnson has $15,000 to invest. Part of it is put in the bank at 4 percent, and part he puts in a savings and loan at 7 percent. If his yearly (simple) is $951, how much did he invest at each rate?
Answers
Answer:
$3300 at 4%
$11700 at 7%
Step-by-step explanation:
Total investment = $15000
Total simple interest on investment = $951
Investment A:
Rate = 4% =0.04
Investment B:
Rate = 7% =0.07
Simple interest (S. I) = principal * rate * time
(S. I on investment A + S. I on investment B)
Let principal amount in investment A = A
principal amount in investment B = B
(A * 0.04 * 1) + (B * 0.07 * 1) = $951
0.04A + 0.07B = $951 - - - - (1)
A + B = $15000 - - - - (2)
from (2)
A = 15000 - B
Substitute A = 15000 - B into (1)
0.04(15000 - B) + 0.07B = 951
600 - 0.04B + 0.07B = 951
600 + 0.03B = 951
0.03B = 951 - 600
0.03B = 351
B = 351 / 0.03
B = $11700
From (2)
A + B = $15000
A + $11700 = $15000
A = $(15000 - 11700)
A = $3300
Past data indicate that the amount of money contributed by the working residents of a large city to a volunteer rescue squad is a normal random variable with a standard deviation of $1.40. It has been suggested that the contributions to the rescue squad from just the employees of the sanitation department are much more variable. If the contributions of a random sample of 12 employees from the sanitation department have a standard deviation of $1.75, can we conclude at the 0.01 level of significance that the standard deviation of the contributions of all sanitation workers is greater than that of all workers living in the city?
Answers
Answer:
We fail to reject the Null and conclude that the standard deviation of the contributions of all sanitation workers is not greater than that of all workers living in the city.
Step-by-step explanation:
σ = 1.40 ; σ² = 1.40² = 1.96
H0 : σ² = 1.96
H0 : σ² > 1.96
Given that:
Sample size, n = 12
Population Standard deviation, σ = 1.40
Sample standard deviation, s = 1.75
α = 0.01
The test statistic :
χ² = [(n-1)s²] ÷ σ²
χ² = [(12 - 1) * 1.75²] ÷ 1.40²
χ² = (11 * 3.0625) ÷ 1.96
χ² = 33.6875 / 1.96
χ² = 17.1875
χ² = 17.19
Using the Pvalue from Chisquare score calculator;
df = n - 1 ; 12 - 1 = 11
Pvalue ; χ²(17.19, 11) = 0.10238
Since Pvalue > α ; We fail to reject the Null and conclude that the standard deviation of the contributions of all sanitation workers is not greater than that of all workers living in the city.
Help plz................ Easy.......

Answers
Step-by-step explanation:
120° because opposite angles of parm are equal
Dean invested $1100 into a bond. When the bond's maturity date was reached five
years later, Dean had a total of $1500. What is Dean's rate of return on investment?
Answers
Answer:
About 36%.
Step-by-step explanation:
The formula for the rate of return on investment is the total value minus the initial cost divided by the initial cost.
The total value is $1,500. The initial cost is $1,100.
(1,500 - 1,100) / 1,100 = 400 / 1,100 = 4 / 11 = 0.363636363636
So, Dean's rate of return on investment is about 36%.
Hope this helps!
Which is the graph of f(x) = (2)-x?
Answers
_____
B
_________
?
______________