Summary of the data on two variables to be presented simultaneously is called a. simultaneous equations b. a histogram c Pivot table
Answers
A pivot table is summary of the data on two variables to be presented simultaneously .
A pivot table, is a data summarization tool used in spreadsheet programs or database software. It allows for the transformation and restructuring of data, enabling users to extract meaningful insights by summarizing and analyzing large datasets. The intersection cells of the table contain summary statistics or aggregated values, such as counts, sums, averages, or percentages, representing the relationship between the two variables. Pivot tables provide a concise and structured way to analyze and present data from multiple perspectives, facilitating data exploration and making it easier to identify patterns, trends, and relationships between variables.
To know more about pivot table click here :
https://brainly.com/question/29786913
#SPJ4
Related Questions
Use a maclaurin series in this table to obtain the maclaurin series for the given function. F(x) = x cos(5x)
Answers
By using a maclaurin series to obtain the maclaurin series for the given function is F(x) = x cos(5x) = \(1 - 25x^2/2! + 625x^4/4! - 15625x^6/6! + ...\)
To obtain the Maclaurin series for the function f(x) = x cos(5x), we need to write the Maclaurin series for cos(5x). The Maclaurin series for cos(x) is: \(cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + ...\)
Using this formula, we can substitute 5x for x and obtain the Maclaurin series for cos(5x): cos(5x) =\(1 - (5x)^2/2! + (5x)^4/4! - (5x)^6/6! + ...\)
\(= 1 - 25x^2/2! + 625x^4/4! - 15625x^6/6! + ...\)
We can substitute this series into the original function f(x) = x cos(5x) and obtain its Maclaurin series: f(x) = x cos(5x)
\(= x[1 - 25x^2/2! + 625x^4/4! - 15625x^6/6! + ...]\)
\(= x - 25x^3/2! + 625x^5/4! - 15625x^7/6! + ...\)
This is the Maclaurin series for the function f(x) = x cos(5x). It is obtained by substituting the Maclaurin series for cos(5x) into the original function and simplifying the resulting series. Maclaurin series are useful for approximating functions using polynomials. By truncating the series after a certain number of terms, we can obtain a polynomial that approximates the original function to a certain degree of accuracy. The accuracy of the approximation depends on the number of terms in the series that are used. The more terms we include, the more accurate the approximation will be.
Learn more about polynomials here:
https://brainly.com/question/11536910
#SPJ4
a teacher grading statistics homework finds that none of the students has made more than three errors. 13% have made three errors, 27% have made two errors, and 40% have made one error. find the standard deviation of the number of errors in students' statistics homework.
Answers
The standard deviation of the number of errors in students' statistics homework is 0.94
The percentage of students made three error = 13%
The percentage of students made two error = 27%
The percentage of students made one error = 40%
The percentage of students made zero error = 100 - (13+27+40)
= 100 - 80
= 20%
Next we have to find the value of E(x)
E(x) = 0.2(0) + 0.4(1) + 0.27(2) + 0.13(3)
= 0 + 0.4 + 0.54 + 0.39
= 1.33
Next find the value of variance
Variance = 0.2(0-1.33)^2 + 0.4(1-1.33)^2 + 0.27(2-1.33)^2 + 0.13(3-1.33)^2
= 0.35378 + 0.04356 + 0.121202 + 0.362557
= 0.8811
Standard deviation = \(\sqrt{0.8811}\)
= 0.94
Therefore, the standard deviation is 0.94
Learn more about standard deviation here
brainly.com/question/23907081
#SPJ4
help meeeeeeeeeeeeeeeeeeee pleaseee rnnnn rn!!!!

Answers
By solving a quadratic equation we will see that the length is L = 12mi and the width is W = 6mi
How to get the length and width?
Remember that for a rectangle of width W and length L the area is:
A = L*W
Here we know that the area is 72 square miles, then we can write the equation:
72 = L*W
And the width is 6 miles less than the length, then:
W = L - 6
Replacing the second equation into the first one we get:
72 = L*(L - 6)
72 = L^2 - 6L
Now we need to solve the quadratic equation:
L^2 - 6L - 72 = 0
The solutions are given by the quadratic formula:
\(L = \frac{6 \pm \sqrt{(-6)^2 - 4*1*(-72)} }{2*1} \\\\L = \frac{6 \pm 18 }{2}\)
The length can only be a positive value, then we take the positive solution:
L = (6 + 18)/2 = 24/2 = 12
The length is 12 miles, and the width is 6 miles less than that, so the width is:
W = 12mi - 6mi = 6mi
Learn more about quadratic equations:
https://brainly.com/question/1214333
#SPJ1
can u help me find the slope
(-5,4) (5,3)
And
(3,1)(1,-1)
Answers
Answer:
For the (-5,4) and (5,3) the slope is -1/10 and the other one's slope is 1
Step-by-step explanation:
Use y2 - y1 over x2-x1
What is the solution to the system of equations? 6 x + 2 y = 6. 7 x + 3 y = 5. (Negative 3, 2) (Negative 1, 6) (2, Negative 3) (6, Negative 1)
Answers
Answer:
(2, -3)
Step-by-step explanation:
These are the steps I used:
(6x+2y=6) x3 -> 18x+6y=18
(7x+3y=5) x2 -> 14x+6y=10
When you subtract the equations you get:
4x=8
x=2
The solution to the system of equations is -3 and -2
The correct option is A
What is a system of equations?A mathematical equation is a statement with two equal sides and an equal sign in between. An equation is, for instance, 4 + 6 = 10. Both 4 + 6 and 10 can be seen on the left and right sides of the equal sign, respectively.
A system of equations is two or more equations that can be solved to get a unique solution. the power of the equation must be in one.
6x+2y=6 is equation (1)
7x+3y=5 is equation (2)
Multiplying equation (1) by (3)
18x+6y=18 is equation(3)
By multiplying (2) by 2
14x+6y=10 is equation (4)
Substrate equation (4) from (3)
4x=8 Now, divide both sides by 4
X=2
Substitute x=2 in (1)
6(2)+2y=6
12+2y=6
Substrate 12 from LHS and RHS
2y=-6
Divide both sides by 2
y=-3
Hence x=2 and y=-3
learn more about system of equations here;
https://brainly.com/question/25180086
#SPJ6
Solve for y. (7x-10) (6y-12)
Answers
Hence, after solving the expression (7x-10)(6y-12)=0, the value of y comes out as y=2.
What is zero product rule?
The zero product property states that if A and B are two real numbers and their multiplication results in zero, then either A or B must equal zero, however it is possible for both A and B to be equal to zero in rare circumstances. As a result, we can state that the product of two real non-zero numbers cannot ever be zero. It is typically applied for solving algebraic problems. Any expression that contains a variable is considered an algebraic expression. A zero-equivalent algebraic expression is referred to as an equation.
Given, the complete mathematical equation is (7x-10)(6y-12) = 0
By Zero Product Rule,
Since the expression is in product form, and it is equal to zero, we can equate each expression to zero.
Thus,
(7x-10) = 0
⇒ 7x = 10
⇒ x = 10/7
For the second expression,
(6y-12) = 0
⇒ 6y = 12
⇒ y = 12/6
⇒ y = 2
Hence, after solving the expression (7x-10)(6y-12)=0, the value of y comes out as y=2.
To know more about zero product rule visit:
brainly.com/question/16989879
#SPJ1
Using Zero product rule, Hence, after solving the expression (7x-10)(6y-12)=0, the value of y comes out as y=2.
What is zero product rule?The zero product property states that if A and B are two real numbers and their multiplication results in zero, then either A or B must equal zero, however it is possible for both A and B to be equal to zero in rare circumstances. As a result, we can state that the product of two real non-zero numbers cannot ever be zero. It is typically applied for solving algebraic problems. Any expression that contains a variable is considered an algebraic expression. A zero-equivalent algebraic expression is referred to as an equation.
Given, the complete mathematical equation is (7x-10)(6y-12) = 0
By Zero Product Rule,
Since the expression is in product form, and it is equal to zero, we can equate each expression to zero.
Thus,
(7x-10) = 0
⇒ 7x = 10
⇒ x = 10/7
For the second expression,
(6y-12) = 0
⇒ 6y = 12
⇒ y = 12/6
⇒ y = 2
Hence, after solving the expression (7x-10)(6y-12)=0, the value of y comes out as y=2.
To know more about zero product rule visit:
brainly.com/question/16989879
#SPJ1
Find the value of x.

Answers
Answer
x=7
Step-by-step explanation:
I honestly forgot how to explain but my logic is that 43+137+137+43=360
so, x would equal 7
MATHEMATICAL CONNECTIONS Write a polynomial in standard form that represents the area of the shaded region.

Answers
Check the picture below.
so since the shaded area is really just the area of those triangles, let's simply get the area of those two triangles with that base and height.
\(2\left[\cfrac{1}{2}\stackrel{ base }{\left( \cfrac{x+6}{2} \right)}\stackrel{ height }{(x+5)} \right]\implies \cfrac{(x+6)(x+5)}{2}\implies \stackrel{ \textit{shaded region} }{\cfrac{x^2+11x+30}{2}}\)

an important first step in assessing the relationship of two interval level variables is to: a. calculate a correlation coefficient. b. look at a scatter plot. c. do a test of significance. d. calculate the variance of the independent variable.
Answers
Option a. calculate a correlation coefficient is the right response because a correlation coefficient measures the strength and direction of the relationship between two interval level variables.
This is because a correlation coefficient measures the strength and direction of the relationship between two interval level variables. It provides a numerical value that ranges from -1 to 1, where -1 indicates a strong negative correlation, 0 indicates no correlation, and 1 indicates a strong positive correlation.
A scatter plot is also useful in visualizing the relationship between two variables, but it does not provide a numerical value like the correlation coefficient. A test of significance and variance calculation are not typically used as first steps in assessing the relationship between two variables.
Hence, option a. calculate a correlation coefficient is the correct answer.
Learn more about "correlation ":
https://brainly.com/question/4219149
#SPJ11
A 3 pound package of ground beef sells for $6. At this rate, if John buys 10 pounds of
ground beef, how much would he pay?
Answers
Answer:
$20
Step-by-step explanation:
3 pounds of beef is 6 dollars.
6 divided by 3 is 2. Therefore, each pound cost $2.
He wants to buy 10 pounds of beef.
9 pounds would be $18.
Add 1 pound, which is $2 and you will get $20.
Therefore, he would pay $20!~
Hope this helps!~~ <3
how many copies for every 10 minutes
Answers
SO
V
120
V
R
1
Find the measure of the missing angle.
70
2
45
ООО
10
3
180
4
Previous
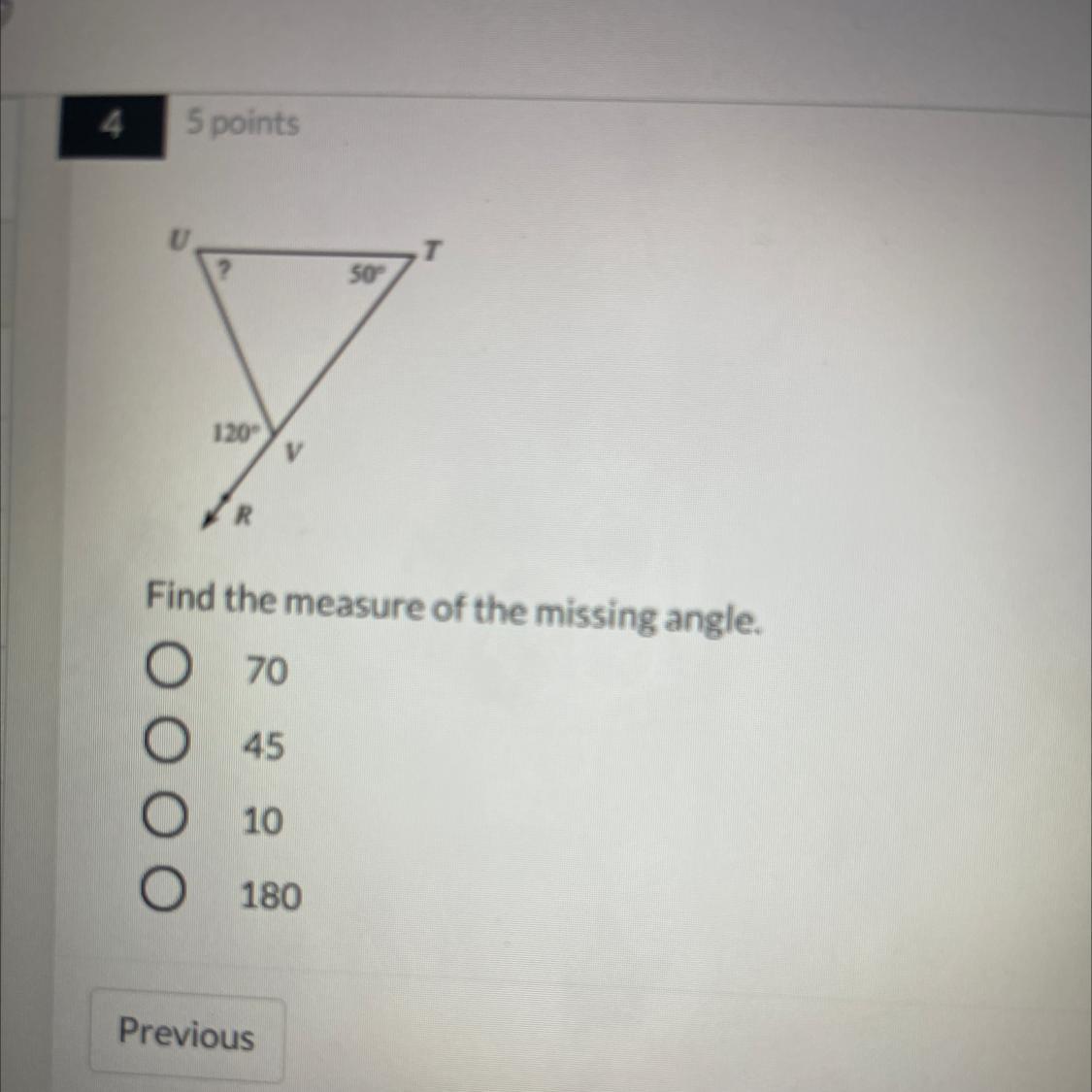
Answers
Answer:
Third option
Step-by-step explanation:
Given the following question where...
\(180 = a1+a2+a3\)
A triangle adds up to 180 degrees
50 + 120 = 170 + 10 = 180
The measurement of the third angle is 10 degrees or the third option.
Hope this helps.
Consider the following differential equations. Determine if the Existence and Uniqueness Theorem does or does not guarantee existence and uniqueness of a solution of each of the following initial value problems.{eq}\begin{array}{l}{\frac{d y}{d x}=\sqrt{x-y}, \quad y(2)=2} \\ {\frac{d y}{d x}=\sqrt{x-y}, \quad y(2)=1} \\ {y \frac{d y}{d x}=x-1, \quad y(0)=1} \\ {y \frac{d y}{d x}=x-1, \quad y(1)=0}\end{array} {/eq}
Answers
Existence and Uniqueness Theorem the existence and uniqueness theorem is the most critical theorem in differential calculus. The theorem addresses how the existence and uniqueness of a solution to a first-order differential equation are affected by conditions such as continuity or Lipschitz continuity.
Determine if the existence and uniqueness theorem does or does not guarantee the existence and uniqueness of a solution to each of the following initial value problems.
1. The differential equation is
\(\frac{dy}{dx}=\sqrt{x-y}\)
The condition of the theorem is fulfilled: The differential equation is continuous and the partial derivative \(\frac{\partial f}{\partial y}=\frac{-1}{2\sqrt{x-y}}\) is continuous.
Therefore, the theorem guarantees the existence and uniqueness of the solution to the initial value problem.
2. The differential equation is
\(\frac{dy}{dx}=\sqrt{x-y}\)
The condition of the theorem is not fulfilled.
\(\frac{\partial f}{\partial y}=\frac{-1}{2\sqrt{x-y}}\) is not defined at \(x=y .\)
Therefore, the theorem does not guarantee the existence and uniqueness of the solution to the initial value problem.
3. The differential equation is \(y\frac{dy}{dx}=x-1\) The condition of the theorem is fulfilled: The differential equation is continuous and the partial derivative \(\frac{\partial f}{\partial y}=y\) is continuous.
Therefore, the theorem guarantees the existence and uniqueness of the solution to the initial value problem.
4. The differential equation is
\(y\frac{dy}{dx}=x-1\)
The condition of the theorem is not fulfilled \(\frac{\partial f}{\partial y}=y\) and is not defined at y=0
Therefore, the theorem does not guarantee the existence and uniqueness of the solution to the initial value problem.
Learn more about the Existence and Uniqueness Theorem at: https://brainly.com/question/30417555
#SPJ11
Shannon's net worth is $872. 17 and her liabilities are $15,997. If she pays off a credit card with a balance of $7,698, what is her new net worth?
Answers
Answer:
To calculate Shannon's new net worth after paying off her credit card, we need to subtract the credit card balance from her total liabilities, and then subtract the result from her net worth:
New liabilities = $15,997 - $7,698 = $8,299
New net worth = $872.17 - $8,299 = -$7,426.83
Based on these calculations, Shannon's new net worth would be -$7,426.83 after paying off her credit card. This indicates that her liabilities still exceed her assets, and she would need to continue working towards reducing her debt and increasing her net worth over time.
To know more about liabilities refer here
https://brainly.com/question/18484315#
#SPJ11
Ann, Deandre, and Bob have a total of $ 94 in their wallets. Bob has 2 times what Ann has. Ann has $10 less than Deandre. How much do they have in their wallets
Answers
Ann has 21, Deandre has 31, and Bob has 42 in their wallets.
Let's start by using variables to represent the amount of money each person has:
Let A be the amount of money Ann has.
Let B be the amount of money Bob has.
Let D be the amount of money Deandre has.
We can then translate the problem into a system of equations:
A + B + D = 94 (the total amount of money they have is 94)
B = 2A (Bob has twice what Ann has)
A = D - 10 (Ann has 10 less than Deandre)
We can use the third equation to substitute A in terms of D in the first two equations:
A = D - 10
B = 2A = 2(D - 10) = 2D - 20
A + B + D = 94 => (D - 10) + (2D - 20) + D = 94 => 4D - 30 = 94 => 4D = 124 => D = 31
So Deandre has 31. We can use the third equation again to find that Ann has 21, and then we can use the second equation to find that Bob has 42.
for such more question on variables
https://brainly.com/question/27761372
#SPJ11
A random sample of 100 people from region A and a random sample of 100 people from region B were surveyed about their grocery store habits.
Answers
By answering the presented question, we may conclude that From the z relations the probability is found to be P(Z = -1.42) = 0.1573
What is null hypothesis?A null hypothesis is a sort of statistical hypothesis that asserts that a certain set of observations has no statistical significance. Sample data is used to assess the feasibility of ideas. H0 represents what is sometimes referred to as "zero." The researchers make the premise that there may be a link between the parameters. The null hypothesis, on the other hand, claims that no such association exists. While it may not appear to be relevant, the null hypothesis is a crucial aspect of research.
There is no significant difference between the two regions population proportion of people who go for online shopping
We set the null hypothesis as H₀ : p₁ = p₂
Our alternative hypothesis is then Hₐ : p₁ ≠ p₂
Here we have the test statistic as follows;
\(Z_o = \frac{P_1 - P_2}{\sqrt(\frac{P_1q_1}{n_1} \frac{P_2q_2}{n_2} )}\)
Where:
p₁ = 16%
p ₂= 24%
n₁ = 100 people
n₂ = 100 people
q =1 - p
From the z relations the probability is found to be P(Z = -1.42) = 0.1573
Therefore, as p > α at 0.05, we fail to reject the null hypothesis, and therefore based on the statistical evidence, there is no significant difference between the two regions population proportion of people who go for online shopping.
To know more about null hypothesis visit:
https://brainly.com/question/28920252
#SPJ1
The correct question is -
A random sample of 100 people from region A and a random sample of 100 people from region B were surveyed about their grocery-shopping habits. From the region A sample, 16 percent of the people indicated that they shop for groceries online. From the region B sample, 24 percent of the people indicated that they shop for groceries online.
Mr. Blake took 10 minutes to drive 5 miles,
He claims it will take half an hour to drive 15 more miles at the same rate.
Select all the statements that are true if Mr. Blake claim is true.
1. He will travel 2 miles per minute.
2. Hw would travel 50 miles in 25 minutes.
3. He will travel 1 mile for every 2 minutes.
4. He will travel at a rate of 30 miles per hour.
5. The ratio of miles driven to minutes traveled is 1:2.
Answers
Answer:
The correct answer is - 3, 4, and 5.
Step-by-step explanation:
Given:
distance = 5 miles
time to cover 5 miles = 10 minutes
If his claim is true then,
additional Distance = 15 miles
total distance will be = 15+5 = 20 miles
additional time = 30 minutes
total time = 10+30 = 40 minutes
Solution:
The speed of the vehicle can be calculated by the formula:
V = d/t
where V is speed or velocity
d = distance
t = time
Putting the final or total values in formula =
V = 20/40
= 1/2 (5th statement is true)
In an hour where 60 minutes are there, 1/2 = 30 miles per hour.
Thus, 3rd and 4th statement are true.
See the image below MATHH

Answers
The restricted value on the range of function f(x) is given as follows:
3.
How to obtain the domain and range of a function?The domain of a function is defined as the set containing all the values assumed by the independent variable x of the function, which are also all the input values assumed by the function.The range of a function is defined as the set containing all the values assumed by the dependent variable y of the function, which are also all the output values assumed by the function.From the horizontal dashed line, the function never assumes a value of y = 3, hence the restricted value on the range of function f(x) is given as follows:
3.
Learn more about domain and range at https://brainly.com/question/26098895
#SPJ1
Answer:
3
Step-by-step explanation:
The range of a function is the set of all possible output values (y-values).
The given diagram shows the graph of a rational function with a horizontal asymptote at y = 3 (indicated by the dashed line).
An asymptote is a line that the curve gets infinitely close to, but never touches.
Therefore, as there is an asymptote at y = 3, the curve of the function will never touch the line y = 3, and consequently the value of y = 3 is restricted from the range of the function.
D²y(t) + 12 Dy(t) + 36y(t) = 2 e-5t y(0) = 1, Dy(0)=0 Solve the differemtial equation using Classical Method (30pts) and Laplace Transform Method(30pts)
Answers
The solution to the differential equation D²y(t) + 12 Dy(t) + 36y(t) = 2 \(e^{(-5t)}\), with initial conditions y(0) = 1 and Dy(0) = 0, is \(y(t) = (1 + 6t) e^{(-6t)}\).
To solve the given differential equation using the classical method, we can assume a solution of the form \(y(t) = e^{(rt)}\) and find the values of r that satisfy the equation. We then use these values of r to construct the general solution.
Using the classical method:
Substitute the assumed solution \(y(t) = e^{(rt)}\) into the differential equation:
D²y(t) + 12 Dy(t) + 36y(t) = \(2 e^{(-5t)}\)
This gives the characteristic equation r² + 12r + 36 = 0.
Solve the characteristic equation for r by factoring or using the quadratic formula:
r² + 12r + 36 = (r + 6)(r + 6)
= 0
The repeated root is r = -6.
Since we have a repeated root, the general solution is y(t) = (c₁ + c₂t) \(e^{(-6t)}\)
Taking the first derivative, we get Dy(t) = c₂ \(e^{(-6t)}\)- 6(c₁ + c₂t) e^(-6t).\(e^{(-6t)}\)
Using the initial conditions y(0) = 1 and Dy(0) = 0, we can solve for c₁ and c₂:
y(0) = c₁ = 1
Dy(0) = c₂ - 6c₁ = 0
c₂ - 6(1) = 0
c₂ = 6
The particular solution is y(t) = (1 + 6t) e^(-6t).
Using the Laplace transform method:
Take the Laplace transform of both sides of the differential equation:
L{D²y(t)} + 12L{Dy(t)} + 36L{y(t)} = 2L{e^(-5t)}
s²Y(s) - sy(0) - Dy(0) + 12sY(s) - y(0) + 36Y(s) = 2/(s + 5)
Substitute the initial conditions y(0) = 1 and Dy(0) = 0:
s²Y(s) - s - 0 + 12sY(s) - 1 + 36Y(s) = 2/(s + 5)
Rearrange the equation and solve for Y(s):
(s² + 12s + 36)Y(s) = s + 1 + 2/(s + 5)
Y(s) = (s + 1 + 2/(s + 5))/(s² + 12s + 36)
Perform partial fraction decomposition on Y(s) and find the inverse Laplace transform to obtain y(t):
\(y(t) = L^{(-1)}{Y(s)}\)
Simplifying further, the solution is:
\(y(t) = (1 + 6t) e^{(-6t)\)
To know more about differential equation,
https://brainly.com/question/32622859
#SPJ11
if there are 5 finalists at a singing competition, in how many ways can they be ordered, if they each take turns singing?
Answers
If there are 5 finalists at a singing competition, in 120 ways they can be ordered, if they each take turns singing by applying basic counting principles.
There are 5 finalists at a singing competition and each of them takes turns singing.
We can calculate the number of ways the 5 finalists can take up turn by applying basic counting principles.
Therefore, they can be ordered in n factorial ways, that is n !, where n is the number of finalists who take turns to sing.
Thus, number of ways the finalists can be ordered is = 5!
= 5*4*3*2*1 ( ways )
= 120 ways
To know more about basic principle of counting here
https://brainly.com/question/30971316
#SPJ4
Last year there were 120 students in choir. This year, 30% more students took choir. How many students are taking choir this year?
Answers
Answer:
156 students
Step-by-step explanation:
To find how many students are in choir this year, multiply 120 by 1.3
120(1.3)
= 156
So, this year, 156 students are taking choir
Answer:
156 students
Step-by-step explanation:
120*30%=36
120+36=156
The number of small air bubbles per 3 feet by 3 feet plastic sheet has a Poisson distribution with a mean number of two per sheet. What percent of these sheets have no air bubbles
Answers
The percentage of the sheets with no air bubbles is given as follows:
13.53%.
What is the Poisson distribution?In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following mass probability function:
\(P(X = x) = \frac{e^{-\mu}\mu^{x}}{(x)!}\)
The parameters are listed and explained as follows:
x is the number of successes that we want to find the probability of.e = 2.71828 is the Euler number\(\mu\) is the mean in the given interval or range of values of the input parameter.The mean for this problem is given as follows:
\(\mu = 2\)
The proportion of these sheets with no air bubbles is P(X = 0), hence it is given as follows:
P(X = 0) = e^-2 = 0.1353 = 13.53%.
More can be learned about the Poisson distribution at https://brainly.com/question/7879375
#SPJ1
Is the
statement (-1)n = -1 true for any positive integer n? Explain.
Answers
Answer:
it has to equal -1 x= to -1 parenthesees
1 times -1= -1 its true for that 1 answer but not the others
5. What is "Data Triangulation" in general? Give 2 real-world examples.
Answers
Data triangulation is a research method that involves using multiple data sources or methods to gather and analyze information, enhancing the validity and comprehensiveness of findings.
Data triangulation is a research method that involves using multiple sources or methods to gather and analyze data on a particular topic or research question. By combining different data sources, researchers aim to enhance the validity, reliability, and comprehensiveness of their findings.
Two real-world examples of data triangulation are:
Qualitative-Quantitative Triangulation in Market Research: In market research, qualitative methods like focus groups or interviews can be combined with quantitative methods like surveys or sales data analysis. By triangulating these data sources, researchers can gain a deeper understanding of consumer preferences, behaviors, and market trends, combining the richness of qualitative insights with the statistical power of quantitative data.Methodological Triangulation in Educational Research: In educational research, methodological triangulation can be employed by using multiple research methods to investigate a learning phenomenon. For example, a researcher may use classroom observations, interviews with teachers, and student performance data to gain a comprehensive understanding of a teaching strategy's effectiveness. By triangulating these data sources, the researcher can capture a more complete picture of the learning environment and draw robust conclusions.Learn more about Data Triangulation at
https://brainly.com/question/30027711
#SPJ4
A random sample of 155 observations results in 62 successes. [You may find it useful to reference the z table.]a. Construct the a 90% confidence interval for the population proportion of successes. (Round intermediate calculations to at least 4 decimal places. Round "z" value and final answers to 3 decimal places.)b. Construct the a 90% confidence interval for the population proportion of failures. (Round intermediate calculations to at least 4 decimal places. Round "z" value and final answers to 3 decimal places.)
Answers
For a random sample of 155 observations results in 62 successes.
a) A 90% confidence interval for the population proportion of successes is equals to the (0.335 , 0.465).
b) A 90% confidence interval for the population proportion of failure is equals to the (0.535 , 0.665).
We have a random sample of 155 observations results in 62 successes. So,
Observed value, x = 62
Sample size,n = 155
Population Proportion, p = x/n
= 62/155
= 0.4
a) We have to determine 90% confidence interval for the population proportion of successes. Using the distribution table, for 90% confidence interval, z-score value is equals to 1.6. Consider Confidence interval formula with proportion, CI \(= p ± z×\sqrt\frac{p(1-p)}{n}\)
substitute all known values in above formula, \(= 0.4 ± 1.64\sqrt\frac{0.4(1- 0.4)}{155}\)
= 0.4 ± 0.0645
= (0.4 - 0.0645 , 0.4 + 0.0645)
= (0.335 , 0.465)
b) Now, we have to determine a 90% confidence interval for the population proportion of failures.
Now consider, here failure observed values, x = 155 - 62
= 93
proportion, p = x/n
= 93/155 = 0.6
Consider the confidence interval formula, CI \(= p ± z×\sqrt\frac{p(1-p)}{n}\)
substitute values, \(= 0.6 ±1.64×\sqrt\frac{0.6(1-0.6)}{155}\)
= 0.6 ± 0.0645
= (0.6 - 0.0645 , 0.6 + 0.0645)
= (0.535 , 0.665)
Hence, required value is (0.535 , 0.665).
For more information about confidence interval, visit :
https://brainly.com/question/17212516
#SPJ4
Here are the first 4 terms in the sequences
3,9,15,21
next term=27
explain how you got the answer
Answers
A series of numbers called an arithmetic progression or arithmetic sequence has a constant difference between the terms.
An arithmetic progression with a common difference of 2 is found, for instance, in the numbers 5, 7, 9, 11, 13, and 15. Given that each term has a common difference, this is an arithmetic sequence.
In this instance, the result is obtained by adding 6 6 to the prior term in the sequence.
What is the arithmetic progression formula?
a {n}=a {1}+(n-1) The nth term in the series is d a n.
The first term in the sequence is a 1.
d is the common distinction between the terms.
To learn more about Arithmetic progression refer to:
https://brainly.com/question/24191546
#SPJ13
the ratio of men to women in a certain factory is 3 to 4. there are 216 men.
how many worker are there?
Answers
Answer:
288
Step-by-step explanation:
3/4=216/x
then solve
864=3x
x=288
Write an example problem(s) for area.
Answers
Answer:
Example 1.
A square with side lengths of 5.
5*5 = 25.
So the area would be 25 units ^2
Example 2.
A rectangle with a length of 9 and a width of 4
9*4 = 36
So the area is 36 units ^2
Answer:
A square with side lengths of 5.5*5 = 25.
Step-by-step explanation:
A researcher measures the time it takes eight participants to complete three successive tasks. What are the degrees of freedom between persons for a one-way repeated-measures ANOVA
Answers
The degrees of freedom between persons are calculated as follows:
df_between = k - 1
where k is the number of groups (in this case, the number of participants), and -1 represents the constraint that the overall mean must be calculated from the group means.
Since there are eight participants in this study, the degrees of freedom between persons for a one-way repeated-measures ANOVA would be:
df_between = 8 - 1 = 7
Therefore, there are 7 degrees of freedom between persons in this study.
I don’t know which one to pick

Answers
\(\sf{\bold{\green{\underline{\underline{Given}}}}} \)
⠀⠀⠀⠀
w = 7a + 4b______________________
\(\sf{\bold{\green{\underline{\underline{To\:Find}}}}} \)
⠀⠀⠀⠀
Correct option = ??______________________
\(\sf{\bold{\green{\underline{\underline{Solution}}}}} \)
⠀⠀⠀⠀
W = 7a + 4b
⠀⠀⠀⠀
Using equations formulae⠀⠀⠀⠀
\(\sf \implies W - 4b = 7a \)
⠀⠀⠀⠀
\(\sf \implies \dfrac{W - 4b}{7} = a \)
⠀⠀⠀⠀
checking correct option⠀⠀⠀⠀
Option 1 :
⠀⠀⠀⠀
\(\sf \bigg( a = \dfrac{W - 4b}{7} \bigg) \neq \bigg( a = \dfrac{W - 7b}{4}\bigg) \)
⠀⠀⠀⠀
This option is not correct
⠀⠀⠀⠀
Option 2 :
⠀⠀⠀⠀
\(\sf \bigg( a = \dfrac{W - 4b}{7} \bigg) \neq \bigg( a = \dfrac{W}{7} - 4b \bigg) \)
⠀⠀⠀⠀
This option is not correct
⠀⠀⠀⠀
Option 3 :
⠀⠀⠀⠀
\(\sf \bigg( a = \dfrac{W - 4b}{7} \bigg) = \bigg( a = \dfrac{W - 4b}{7}\bigg) \)
⠀⠀⠀⠀
This option is correct
⠀⠀⠀⠀
Option 4 :
⠀⠀⠀⠀
\(\sf \bigg( a = \dfrac{W - 4b}{7} \bigg) \neq \bigg( W = \dfrac{W}{7} - 28b \bigg) \)
⠀⠀⠀⠀
This option is not correct
______________________
\(\sf{\bold{\green{\underline{\underline{Answer}}}}} \)
⠀⠀⠀⠀
Correct answer = option C