Answers
Answer:
use Pythagorean theorem:
BC^2 = 7^2 - 4^2 = 33 or BC = sqrt(33)
BC --> opp. AB --> adj
tan A = opp/adj = sqrt(33)/4
Related Questions
If a gallon of gas costs $1.85, how many gallons would you purchase for $15.54?
Answers
Answer:
8.4 Gallons
Step-by-step explanation:
The answer is 8.4 because 15.54 divided by 1.85 is 8.4
Answer:
About 8.4 gallons
Step-by-step explanation:
15.54/1.85=8.4
(15 POINTS IF CORRECT) The width of a rectangle is 3cm less than the length. If the area of a rectangle is 10cm^2, find the length and width.
Answers
Answer:
Length = 5cm, Width = 2cm
Step-by-step explanation:
W = L - 3
LW = 10
L(L-3)= 10
L²-3L-10=0
(L-5)(L+2)=0
L=5
W=2
Answer:
w is 2
L is 5
very sure
What is the Answer to: 120 Times 2/3
Answers
Answer:
80
Step-by-step explanation:
You could multiply by 2 and then divide by 3
120*2 = 240
240/3 = 80
Or you could divide by 3 and then multiply by 2
120/3 = 40
40*2 = 80
Answer:
80Step-by-step explanation:
120 × 2/3= 120/1 × 2/3= 240/3= 80\(\tt{ \green{P} \orange{s} \red{y} \blue{x} \pink{c} \purple{h} \green{i} e}\)
The problem is y=0.75x+5

Answers
30°
What is the value of z?
Z=
35°
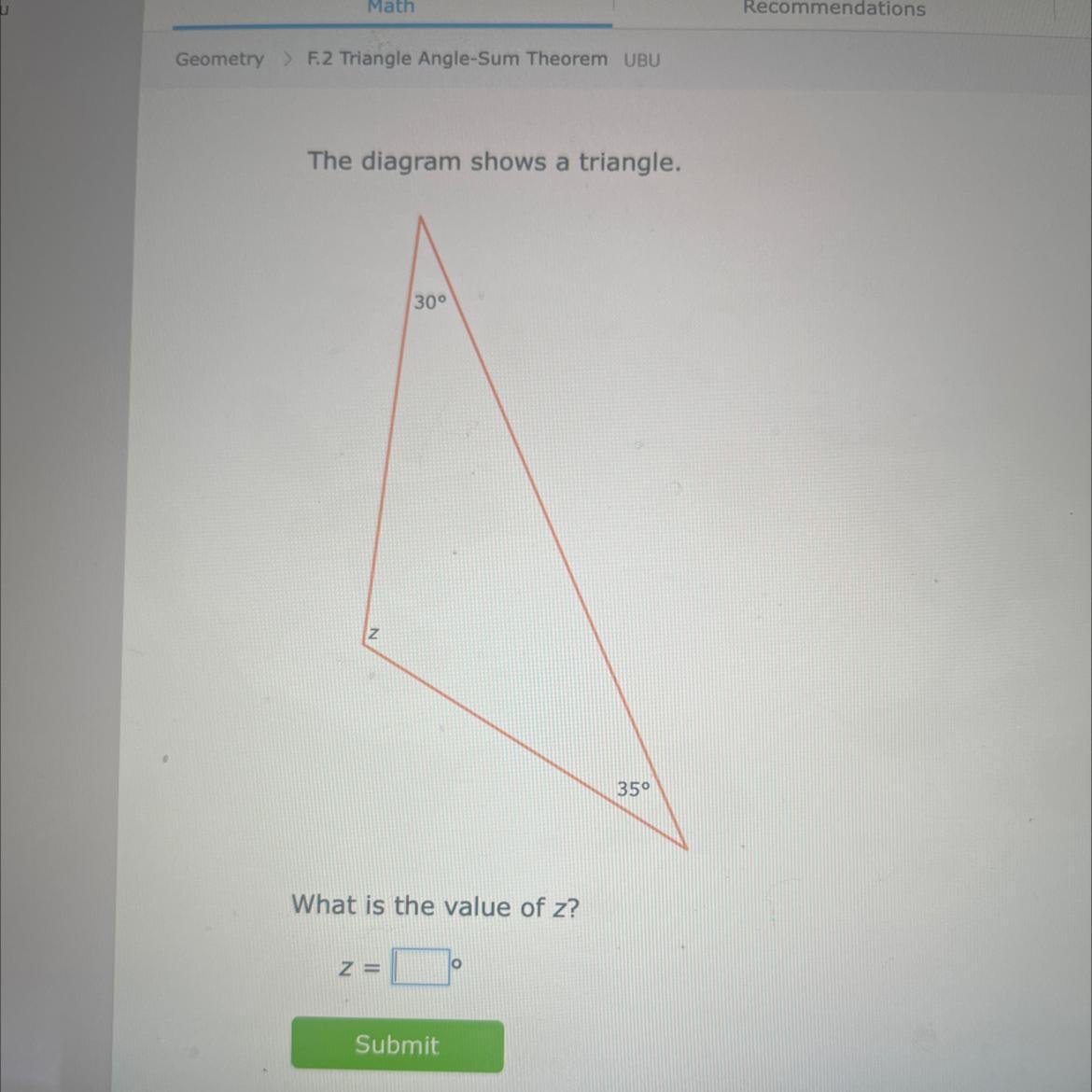
Answers
Answer: 115°
Step-by-step explanation:
The angles in a triangle add up to 180
Z+35+30=180
Z+65=180
Z=115
Some one help pleaseeere

Answers
Answer:
m = 2/3, you were correct
Step-by-step explanation:
plot the point on a graph
calculate the rise by going up alongside the y axis
the rise is 2
calcualte the run it takes to get to the second point
the run is 3
m = rise/run = 2/3
m = 2/3
Plz mark as brainliest if correct! Have a nice day!!!
What la 1 /2 divided by 3/5
Answers
Answer:
\(\frac{5}{6}\)
Step-by-step explanation:
Two fractions
\(\frac{1}{2} / \frac{3}{5}\)
Divide
______________
When dividing two fractions we follow KFC :
Keep
Change
Flip
Keep meaning to keep the fractions
Change meaning to change the division sign to the multiplication sign
Flip meaning to flip the second fraction.
KEEP -
\(\frac{1}{2} / \frac{3}{5}\)
CHANGE -
\(\frac{1}{2} * \frac{3}{5}\)
FLIP -
\(\frac{1}{2} * \frac{5}{3}\)
Multiply across :
\(\frac{1*5}{2*3}\)
\(\frac{5}{6}\)
Answer:
the answer is 5/6
Step-by-step explanation:
1/2 ÷ 3/5
= 5/6
(3 + 4i) + (5 − 2i) (2 points) −2 + 6i 2 − 2i 7 + 3i 8 + 2i
Answers
Answer:
8+2i
Step-by-step explanation:
Combine like terms
3+5=8
4i-2i=2i
Answer: 8 + 2i
Step-by-step explanation:
1) Rewrite the two complex numbers in standard form: (3 + 4i) + (5 − 2i) = 3 + 5 + 4i - 2i = 3 + 5 + 2i
2) Add the real parts and the imaginary parts separately: Real parts: 3 + 5 = 8 Imaginary parts: 2i + (-2i) = 0
3) Put the results in standard form: 8 + 0i = 8 + 0i = 8 + 0i = 8 + 0i = 8 + 0i = 8 + 2i
1. Kane earns an annual salary of $42,500.
He is paid twice a month with paychecks being
of equal amounts. If Medicare taxes
represent 1% of his income, then how much
will Kane bring home after Medicare taxes?
Answers
Answer:
$1753.13
Step-by-step explanation:
Kane's Annual Salary = $42,500
Gross Pay = $42,500
Net Pay = Gross Pay - 1% of Gross Pay
=42500 - (0.01 X 42500)
=$42,075
Since he is paid twice a month with paychecks being of equal amounts.
Number of Payments in a Year =12 X 2= 24
Therefore, Kane's Take Home pay after Medicare taxes
\(= \$42075 \div 24\\=\$1753.13$ (to the nearest cent)\)
Remy wanted to measure the angle of the slide in the playground. He used a piece of folded paper that was 10°. He measured that 3 of the folded paper angles would fit in the angle made by the slide. What was the angle of the slide?
Answers
Answer:
30°
Step-by-step explanation:
Since the folded paper can fit into the slide three times, we simply have to multiply 10° by 3:
10° * 3 = 30°
The angle of the slide is 30°
Could someone help me ASAP !!

Answers
Answer:
LSA = 592cm^2.
Step-by-step explanation:
Well LSA is the SA but without the base so the blue square does not count.
So we have to find the area of the triangle which is b*h/2.
So 18.5*16 / 2 is 148.
And since there is 4 triangles with the same dimensions we do 148*4, 592cm^2.
Given: T = (2, -7) X = (–7, 5) Find: 3TX
Answers
Answer:
3TX = 45
Step-by-step explanation:
See attached graph.
Form a right triangle and use length of the the two sides to find the hypotenuse, XT, 15. 3XT = 45

Find the distance between the points (-16, 20) and (-16, -14).2007(-16, 20)161284-20-16-12-8-4048121620-4-812(-16, -14)-16-20units
Answers
Point A
(-16, 20)
Point B
(-16, -14)
The Distance Formula itself is actually derived from the Pythagorean Theorem which is a
\(\begin{gathered} d=\sqrt[]{(y2-y1)^2+(x2-x1)^2} \\ d=\sqrt[]{(-14-20)^2+(-16-(-16}))^2 \\ d=\sqrt[]{(-34)^2} \\ d=34 \end{gathered}\)The distance would be 34 units
calculate the length of the curve c, defined by r(t) = 〈2 cos(t),2 sin(t)〉 with domain of −π/2 ≤t ≤π/2.
Answers
To calculate the length of the curve defined by r(t) = 〈2 cos(t), 2 sin(t)〉 with the domain -π/2 ≤ t ≤ π/2, we need to find the arc length using the following formula:
Arc length = ∫(from a to b) ||r'(t)|| dt
First, let's find the derivative r'(t) of the given vector function r(t):
r(t) = 〈2 cos(t), 2 sin(t)〉
r'(t) = 〈-2 sin(t), 2 cos(t)〉
Next, find the magnitude ||r'(t)|| of the derivative vector:
||r'(t)|| = √((-2 sin(t))^2 + (2 cos(t))^2)
||r'(t)|| = √(4 sin^2(t) + 4 cos^2(t))
Factor out 4:
||r'(t)|| = √(4(sin^2(t) + cos^2(t)))
Since sin^2(t) + cos^2(t) = 1:
||r'(t)|| = √(4) = 2
Now, we can find the arc length by integrating ||r'(t)|| over the given domain:
Arc length = ∫(from -π/2 to π/2) 2 dt
To integrate, simply multiply the constant by the difference in t:
Arc length = 2(π/2 - (-π/2)) = 2(π) = 2π
So, the length of the curve is 2π.
Lear more about length of the curve from : brainly.com/question/31376454
#SPJ11
make a 3-d surface plot of the function z = cos(x)cos(,./x2 y2)e-i0.2xl in the domain -21t x 21t and -1t y 1
Answers
We can create a 3D surface plot of the function z = cos(x)cos(y)\(e^{-i0.2x}\) in the domain -2π ≤ x ≤ 2π and -π ≤ y ≤ π by using softwares such as MATLAB, Python (with Matplotlib), or Wolfram Alpha.
To make a 3D surface plot of the function z = cos(x)cos(y)e^(-i0.2x) in the domain -2π ≤ x ≤ 2π and -π ≤ y ≤ π, please follow these steps,
1. Identify the function and domain: The function is z = cos(x)cos(y)e^(-i0.2x), and the domain is -2π ≤ x ≤ 2π for x and -π ≤ y ≤ π for y.
2. Choose a software or tool to create the plot: There are several software and tools available to create 3D surface plots, such as MATLAB, Python (with Matplotlib), or Wolfram Alpha.
3. Define the function in the chosen software/tool: Input the given function into the software, and make sure it is properly formatted.
4. Define the domain in the chosen software/tool: Specify the range for x and y, which is -2π to 2π for x, and -π to π for y.
5. Create the 3D surface plot: Use the plotting function in the chosen software/tool to generate the 3D surface plot of the given function within the specified domain.
6. Analyze the plot: Once the plot is generated, you can analyze the characteristics of the function and visualize how it behaves in the given domain.
By following these steps, you will be able to create a 3D surface plot of the function z = cos(x)cos(y)e^(-i0.2x) in the domain -2π ≤ x ≤ 2π and -π ≤ y ≤ π.
Learn more about "MATLAB": https://brainly.com/question/30891746
#SPJ11
Which one doesn't belong with the other three? -3/4-5/8
Answers
One that does not belong to other three fraction is -6/8.
To determine which of these fractions doesn't belong with the other three, we need to compare them and look for any differences or similarities. One way to do this is to convert the fractions to a common denominator, which in this case would be 8.
-3/4 can be rewritten as -6/8 (multiply the numerator and denominator by 2), and -5/8 is already in the form of 5/8.
Now we can compare all four fractions:
-6/8, 5/8, -5/8, -5/8
We can see that three of the fractions have -5/8 in common, while the other fraction (-6/8) is different. Therefore, the answer to the question is -6/8.
To know more about fraction, refer
https://brainly.com/question/78672
#SPJ11
Note: The question given is incomplete. Here is the complete question.
Question: Which one doesn't belong with the other three? -3/4-5/8 -6/8 5/8
What is the area of the shaded region? (Approximate π to be 3.14)

Answers
Answer:
about 113.04 square inches
Step-by-step explanation:
No angles are indicated, so we must assume the sector is 1/4 of the circle. Then its area is 1/4 of that of a circle with radius 12 in:
Circle area = πr²
Sector area = (1/4)π(12 in)² = 36π in²
Sector area ≈ 36(3.14) in² = 113.04 in²
Help plz. With a step by step explanation

Answers
Answer:
See attachment
Step-by-step explanation:
My reasoning and calculations are attached. I didn't get an answer that matches the answer options, but I think the reasoning is valid. Perhaps you can spot a calculation error. Sorry

Solve for x
((x + 3)/4) + (((2x - 12) - 1)/3) = 1
Answers
Answer:
x=5
Step-by-step explanation:
\(((x+3)/4)+(((2x-12)-1)/3)=1\\\frac{x+3}{4} +\frac{2x-12-1}{3} =1\\\frac{x+3}{4} +\frac{2x-13}{3} =1\\\)
Now we have to cross multiply the denominator to progress further.
\(\frac{3(x+3)}{4*3} +\frac{4(2x-13)}{3*4} =1\\\frac{3x+9}{12} +\frac{8x-52}{12} =1\\\frac{3x+9+(8x-52)}{12} =1\\\frac{3x+9+8x-52}{12} =1\\\frac{11x-43}{12} =1\\11x-43=12\\11x=43+12\\11x=55\\x=\frac{55}{11} \\=5\)
what is the probability that you reach into the jar and randomly grab a quarter and then, without replacement, a nickel? express your answer as a fraction or a decimal number rounded to four decimal places.
Answers
0.688 will be the probability of getting a nickel from the jar.
Given,
Probability;-
Simply put, probability is the likelihood that something will occur. When we don't know how an event will turn out, we can discuss the likelihood or likelihood of several outcomes. Statistics is the study of events that follow a probability distribution.
Here,
The number of fortunate situations divided by the total number of coins would be the product between the probability of each occurrence and the likelihood of each event.
Therefore,
P(nickel) = 19/69
P(penny) = 17/68
That is,
P = 19/69 × 17/68
P = 323/4692
P = 0.0688
That is,
The probability of getting nickel from the jar is 0.06888
Learn more about probability here;
https://brainly.com/question/29087823
#SPJ4
Find the Laplace transform of the following functions f(t) = e^2t cos h(5t) - t sin (2t)
Answers
The Laplace transform of the function f(t) = e²ᵗ cosh(5t) - t sin(2t) is 1/(s - 2) * (s/(s² - 25)) - 2/(s² - 4)².
To find the Laplace transform of the function f(t) = e²ᵗ cosh(5t) - t sin(2t), we can use the linearity and the Laplace transform formulas. Here's the solution:
Applying the linearity property, we can find the Laplace transform of each term separately.
Laplace transform of e²ᵗ cosh(5t):
Using the formula for the Laplace transform of eᵃᵗ f(t):
L{e²ᵗ cosh(5t)} = 1/(s - 2) * (s/(s² - 25))
Laplace transform of t sin(2t):
Using the formula for the Laplace transform of tⁿ f(t):
L{t sin(2t)} = 2/(s² - 4)²
Now, adding the Laplace transforms of the individual terms:
L{f(t)} = 1/(s - 2) * (s/(s²- 25)) - 2/(s² - 4)²
To know more about Laplace transforms, visit:
https://brainly.com/question/32246577
#SPJ11
The size P of a certain insect population at time t (in days) obeys the function P(t)=500e 0.07t
. (a) Determine the number of insects at t=0 days. (b) What is the growth rate of the insect population? (c) What is the population after 10 days? (d) When will the insect population reach 700 ? (e) When will the insect population double? (a) What is the number of insects at t=0 days? insects (b) What is the growth rate of the insect population?
Answers
(a) The number of insects at t=0 days is 500.
(b) The growth rate of the insect population is 7%.
(c) The population after 10 days is \(500 * e^(0.07 * 10)\)insects.
(d) The insect population will reach 700 insects at t = ln(700/500) / 0.07 days.
(e) The insect population will double at t = ln(2) / 0.07 days.
(a) To find the number of insects at t=0 days, we substitute t=0 into the function P(t)=\(500e^(0.07t).\)This gives us \(P(0)=500e^(0.07*0)=500e^0=500\).
(b) The growth rate of the insect population can be determined by examining the coefficient of t in the exponent of the function. In this case, the coefficient is 0.07. To convert this to a percentage, we multiply by 100, resulting in a growth rate of 7%.
(c) To find the population after 10 days, we substitute t=10 into the function \(P(t)=500e^(0.07t).\)This gives us \(P(10)=500e^(0.07*10)=500e^0.7\).
(d) To find when the insect population reaches 700, we set P(t)=700 and solve for t. This gives us 700=\(500e^(0.07t).\)We can solve this equation using logarithms to find the value of t.
(e) To find when the insect population doubles, we set P(t)=2P(0) and solve for t. This gives us 2500=\(500e^(0.07t),\) which can be solved using logarithms.
In summary, the number of insects at t=0 days is 500, and the growth rate of the insect population is 7%.
Learn more about population here
https://brainly.com/question/31598322
#SPJ11
how many degrees does the minute hand of a clock turn in 45 minutes
Answers
The clock minutes rotate 270 degrees in 45 minutes.
How to calculate the angular size of a clock's handsWhile rotating, the clock's hands are seen to move at a speed of six degrees per minute.
The number of degrees for a clock minute is solved by
60 minutes = 360 degrees
1 minute = ?
cross multiplying
60 * ? = 360
? = 360 / 60
? = 6
hence 1 minute is 6 degrees
The formula to use to get the calculation is multiplying the number of minutes by 6
Number of degrees in 45 minutes = 45 * 6
Number of degrees in 45 minutes = 270 degrees
Learn more about clock rotation:
brainly.com/question/28741125
#SPJ1
The Theatre club draws a tree on the set background. The plan for the size of the tree is shown below. What is the approximate area they will have to paint to fill in this tree?
Answers
There are 120 people in a theatre. 72 are female and 48 are male. 12 females purchase an ice cream and 31 males purchase an ice cream.
What is Frequency Tree?Frequency trees display the real frequency of certain events. They can display the same data as a two-way table, but frequency trees are more readable since they illustrate the frequency hierarchy. Probability trees depict the likelihood of a series of occurrences.
Solution:
From the question, we can see the there are 120 people in the theatre.
Since, there are 72 females in the theatre we can find the total number of males by 120-72 = 48
Also, the male who purchased Ice Cream were 36 therefore, the males who did not purchased Ice Cream are 48-36 = 12
And, the females who purchased Ice Cream are 41. So, the female who did not purchased Ice Cream are 72 - 41 = 31
To learn more about Frequency Tree from the given link
brainly.com/question/20433037
#SPJ1
complete question"
there are 120 people in a theatre 72 are female of these 41 purchase an ice cream 36 males purchase and ice cream use this information to compete the frequency tree
Greg started to run on a treadmill after setting it’s timer for 98 minutes the display says that he has finished 57% of his run how many minutes have gone by
Answers
A total of 55.86 minutes have gone by since Greg started his run on the treadmill.
How many minutes have gone byIf Greg has completed 57% of his run, it means he has 43% of his run remaining.
To find out how many minutes have gone by, we can use proportions.
Let's say x is the total number of minutes Greg needs to complete his run:
x = 57% * 98 minutes
Evaluate
x = minutes
Therefore, approximately 55.86 minutes have gone by since Greg started his run on the treadmill.
Read more about proportion at
https://brainly.com/question/1781657
#SPJ1
50 POINTS!!! I WILL GIVE BRAINLIEST TO WHOEVER SHOWS STEPS! THANK YOU!:)))
Show all steps on how you found the answer.
For each function, what is the output of the given input?
For f (x) =4x+7, find f(4)
Answers
Answer:
23
Step-by-step explanation:
If you have something that says it is the f(x) or just f(something) then that is just telling you what the x equals. In this case, x=4 so you plug that into the equation.
This gives you f(4)=4(4)+7. From here, you will use the order of operations to solve.
f(4)=4*4+7
f(4)=16+7
f(4)=23
Answer:
f(4)=23
Step-by-step explanation:
1.f(4)=4(4)+7
2.f(4)=16+7
3.f(4)=23
hope this helps!
Find the exact length of the curve. y = In(sec(x)), 0≤x≤ Need Help? Read It π 4 Watch It
Answers
The curve is y = In(sec(x)) and we have to find its length. We are given the range as 0 ≤ x ≤ π/4. So, the formula for the length of the curve is given as:
To solve for the length of the curve of y = In(sec(x)), we use the formula,
`L = ∫[a,b] √[1+(f′(x))^2] dx`.Where, `a = 0` and `b = π/4`. And `f′(x)` is the derivative of `In(sec(x))`.
We know that:`f′(x) = d/dx[In(sec(x))]`
Using the formula of logarithm differentiation, we can write the above equation as:
`f′(x) = d/dx[In(1/cos(x))]`
So,`f′(x) = -d/dx[In(cos(x))]`
Therefore,`f′(x) = -sin(x)/cos(x)`
Substituting the values, we get:
`L = ∫[a,b] √[1+(f′(x))^2] dx`
`L = ∫[0,π/4] √[1+(-sin(x)/cos(x))^2] dx`
`L = ∫[0,π/4] √[(cos^2(x)+sin^2(x))/(cos^2(x))] dx`
`L = ∫[0,π/4] sec(x) dx`
Now, `L = ln(sec(x) + tan(x)) + C` where `C` is a constant.
We calculate the constant by substituting the values of `a = 0` and `b = π/4`:
`L = ln(sec(π/4) + tan(π/4)) - ln(sec(0) + tan(0))`
`L = ln(√2 + 1) - ln(1 + 0)`
`L = ln(√2 + 1)`
Thus, the exact length of the curve is `ln(√2 + 1)` units.
Thus, the exact length of the curve of y = In(sec(x)), 0≤x≤π/4 is `ln(√2 + 1)` units.
To know more about derivative visit:
brainly.com/question/25324584
#SPJ11
the population of a certain country is about 94
million . the overall birth rate is 16.8 births per 1000 .
approximately how many births were there in the country?
Answers
There were 1,579,200 births in the country.
To calculate the approximate number of births in the country, we can use the formula:
Number of births = (Population / 1000) * Birth rate
Given that the population is about 94 million (94,000,000) and the birth rate is 16.8 births per 1000, we can substitute these values into the formula:
Number of births = (94,000,000 / 1000) * 16.8
Number of births = 1,579,200
Therefore, there were approximately 1,579,200 births in the country.
To know more about births refer to-
https://brainly.com/question/27930769
#SPJ11
Consider the equation y = negative 2 x + 5. Create a table of five ordered pairs that satify the equation. What is the slope of the line represented by the equation? a. M = 2 b. M = 5 c. M = negative 2 d. M = negative 5.
Answers
Answer: C
Step-by-step explanation:
Slope is the number right in front of x, which in this case would be -2. So C is the answer.
Creating a table is hard, so I'll try my best. Just pretend the vertical line is connected.
x|y
0|5
1|3
2|1
3|-1
4|-3
b) Find the value of (2.63 - 0.87) – 2.076
Answers
Answer:
-0.316
Step-by-step explanation:
2.63-0.87-2.076
=-0.316
Hope it helped!
