statistical significance: a. indicates a high likelihood that your results are due to your treatment versus due to chance. b. is more likely to be reliable if you have a small sample size versus a large sample size. c. is a requirement of the data from a scientific experiment. d. indicates that the hypothesis should be rejected. e. depends on large data sets.
Answers
Answer:
Step-by-step explanation:
sean
Related Questions
Help
I will give you 20 points

Answers
Answer:
c)-4/3
Step-by-step explanation:
perpendicular slope is opposite and reciprocal
the green line has a slope of 3/4
so the slope of the red line is -4/3
Write the equation of the line in Point-Slope Form given the information below. Slope=-1/5 y-intercept=-3
Answers
Answer:
your correct answer is y=-1/5-3
Step-by-step explanation:
The linear equation of the line is y = -1/5x - 3 and y + 3 = -1/5(x - 0)
How to determine the line equation?The slope is given as:
m = -1/5
The y-intercept is given as:
c = -3
A linear equation in slope intercept form is represented as:
y = mx + c
So, we have:
y = -1/5x - 3
The equation in point slope form is calculated as follows:
y = -1/5x - 3
Add 3 to both sides
y + 3 = -1/5x
Express -1/5x as -1/5(x)
y + 3 = -1/5(x)
Subtract 0 from x
y + 3 = -1/5(x - 0)
Hence, the linear equation of the line is y = -1/5x - 3 and y + 3 = -1/5(x - 0)
Read more about linear equation at:
https://brainly.com/question/1884491
#SPJ9
On Monday, Lexi rode 3 miles on a bike. On Tuesday, she rode 3 times more than she did Monday. On Wednesday, she rode an additional 4 miles.
How many miles has Lexi ridden so far this week?
Answers
Answer:
she has rode 16 miles this week
Step-by-step explanation:
3 miles on monday 3 times that many on tuesday plus 4 miles one wensaday add them all up
3 times 3 is 9 plus 3 is 12 plus 4 is 16 there fore 16 miles in totale
sorry for my speling erros
She rode a total distance of 16 miles this week.
An expression in mathematics is a combination of terms both constant and variable. For example, we can write the expressions as -
2x + 3y + 5
2z + y
x + 3y
The distance rode by Lexi per day is mentioned below -
Monday - Lexi rode 3 miles on a bike.
Tuesday - Lexi rode 3 times more than she did Monday.
Wednesday - Lexi rode an additional 4 miles.
We can write the expression to find the total distance in miles covered by Lexi as -
d = d{M} + d{T} + d{W}
d = 3 + (3 + 3) + 4
d = 3 + 6 + 4
d = 13 miles
Therefore, she rode a total distance of 16 miles this week.
To solve more questions on equivalent expression, visit the link-
https://brainly.com/question/1041084
#SPJ2
For an experiment, Sandra needs 20 grams of a 26% solution of salt. She has two large bottles of salt water: one contains a 20% solution, and the other contains 35% solution. How much of each must she use to make the solution she needs?
Answers
The amount of grams that she must use to make the solution she needs are: 12 grams and 8 grams.
Amount of gramsx grams of 20% and 20-x grams of 35%
Hence:
0.20x+0.35(20-x)=0.26×20
0.20x-0.35x+7=5.2
Collect like terms
-0.15x=-1.80
Divide both side by -0.15x
x=-1.80/-0.15
x=12 grams of 20% or 2.4 grams pure
20-x= (20-12) =8 grams of 35% or 2.8 grams pure
Therefore the amount of grams that she must use to make the solution she needs are: 12 grams and 8 grams.
Learn more about amount of grams here:https://brainly.com/question/1107267
#SPJ1
A significance test about a proportion is conducted using a significance level of 0.05. The sample statistic is 0.12. The p-value is 0.03? a) If H0 were true, for what probability of a Type I error was the test designed?
b) What conclusion (reject or fail to reject) would you make for this test?
c) If this test resulted in a decision error, what type of error was it?
Answers
Answer: 28282
Step-by-step explanation:
I think
An airplane factory made 36 airplanes per month. At this rate, how many airplanes can the factory make per year?
Answers
The number of planes manufactured by the aeroplane company will be 432.
What is an expression?The mathematical expression combines numerical variables and operations denoted by addition, subtraction, multiplication, and division signs.
Mathematical symbols can be used to represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping. They can also denote the logical syntax's operation order and other properties.
Given that an aeroplane factory made 36 aeroplanes per month. The number of aeroplanes made in a year will be calculated as:-
Number = 36 x Months in a year
Number = 36 x 12
Number = 432
Therefore, the number of planes will be 432.
To know more about an expression follow
https://brainly.com/question/2680080
#SPJ1
e:f = 2:3 and f:g = 5:4 work our e:g
Answers
Answer:
5/6
Step-by-step explanation:
e/f = 2/3
Then
e= 2f/3
f/g = 5/4
Then
g= 4f/5
So
e/g= 2f/3 / 4f/5 = 1/3 * 5/2 = 5/6
Answer:
5/6
Step-by-step explanation:
e/f = 2/3 After that e= 2f/3 f/g = 5/4 So then g= 4f/5 at last
e/g= 2f/3 / 4f/5 = 1/3 x 5/2 = 5/6Assume that x and y are both differentiable functions of t and find the required values of dy/dt and dx/dt. y=√x (a) Find dy/dt, given x = 16 and dx/dt = 3. dy/dt (b) Find dx/dt, given x=25 and dy/d
Answers
The value of dy/dt is 0 units per second.
a) Given: y= √x Differentiating with respect to t, we get; \(dy/dt = 1/2√x * dx/dt\)
On substituting the values of x and dx/dt in the above equation, we get; dy/dt = 1/2 * √16 * 3= 1.5 units per second
Therefore, the value of dy/dt is 1.5 units per second.
b) Given: \(y= √x\)
Differentiating with respect to t, we get;
\(dy/dt = 1/2√x * dx/dt\)
Let us assume that y = k, where k is a constant that can be determined by the given value of x.
Substituting the values of x and y in the equation, we get; 25 = √x
Therefore, x = 625dx/dt
= 0
(Given)\(dy/dt = 1/2√x * dx/dt\)
dy/dt = 1/2√625 * 0
= 0
Therefore, the value of dy/dt is 0 units per second.
To learn more about Differentiating visit;
https://brainly.com/question/13958985
#SPJ11
The American Medical Association reported: "During the first hour after using cocaine, the user's risk of heart attack increases nearly 24 times. The average (mean) age of people in the study who suffered heart attacks soon after using cocaine was only 44. That's about 17 years younger than the average heart attack patient. Of the 38 cocaine users who had heart attacks, 29 had no prior symptoms of heart disease." Assume that the standard deviation of the age of people who suffered heart attacks soon after using cocaine was 10 years. In a random sample of size 49, what is the probability the mean age at heart attack after using cocaine is greater than 42?
A. 0.4207
B. 0.5793
C. 0.0808
D. 0.9192
Answers
The probability the mean age at heart attack after using cocaine is greater than 42 is 0.9192. Hence, the correct option is D. 0.9192.
The standard deviation of the age of people who suffered heart attacks soon after using cocaine was 10 years. In a random sample of size 49, what is the probability the mean age at heart attack after using cocaine is greater than 42?We are given the following details:
The mean age of people in the study who suffered heart attacks soon after using cocaine was only 44.
Standard deviation = 10
Sample size = 49
Now we need to find the z-score using the formula:
z = (x - μ) / (σ / √n)
wherez is the z-score
x is the value to be standardized
μ is the mean
σ is the standard deviation
n is the sample size.
Substitute the values in the formula as given,
z = (42 - 44) / (10 / √49)z = -2 / (10/7)
z = -1.4
Probability of z > -1.4 can be found using the standard normal distribution table or calculator.
P(z > -1.4) = 0.9192
Therefore, the probability the mean age at heart attack after using cocaine is greater than 42 is 0.9192. Hence, the correct option is D. 0.9192.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
find the standard equation of the sphere. (let r = 8 and c = (9, 2, 5).)
Answers
The standard equation of the sphere is:
x^2 + y^2 + z^2 - 18x - 4y - 10z + 46 = 0
The standard equation of a sphere is given by:
(x - a)^2 + (y - b)^2 + (z - c)^2 = r^2
where (a, b, c) is the center of the sphere and r is the radius.
In this case, the center of the sphere is given by c = (9, 2, 5) and the radius is r = 8.
Substituting these values into the standard equation of the sphere, we get:
(x - 9)^2 + (y - 2)^2 + (z - 5)^2 = 8^2
Expanding and simplifying, we get:
x^2 - 18x + 81 + y^2 - 4y + 4 + z^2 - 10z + 25 = 64
x^2 + y^2 + z^2 - 18x - 4y - 10z + 46 = 0
Therefore, the standard equation of the sphere is:
x^2 + y^2 + z^2 - 18x - 4y - 10z + 46 = 0
To know more about standard equation refer here :
https://brainly.com/question/29059560#
#SPJ11
2
The area of a rectangle is given by the
expression 36cd + 90d. Which of the
following are possible dimensions for
the rectangle?
O A. 9 by 40 + 10d
O B. 36 by cd + 5d
O C. 6d by 6c + 15
OD. 18d by 2c + 5d
Answers
Answer:C
Step-by-step explanation:
6d(6c +15) = 36cd +90d
I don’t know if I’m right


Answers
Answer:
A: geometric; 4 times
B: arithmetic: 4 more
Step-by-step explanation:
An arithmetic model is a linear model, where the rate of change is constant. Growth or decay is by a constant amount from one interval to the next.
A geometric model is an exponential model, in which the rate of change is proportional to the amount. Growth or decay is by a constant factor from one interval to the next.
__
A)The equation for the sequence is given in "explicit" form:
\(A_n=2^{2n}\)
The exponent can be split so this can be rewritten as ...
\(A_n=(2^2)^n=4^n\)
If this were written in recursive form, it would look like ...
\(A_0=1,\ A_n=4\times A_{n-1}\)
The fact that terms are related by a constant factor tells you the model is geometric. The factor tells you each hour the population is 4 times what it was in the previous hour.
__
B)The given equation is in "recursive" form. It tells you each term is 4 more than the previous one. This constant difference between terms means the model is arithmetic.
_____
Additional comment
In general, words like "more" or "increase" refer to addition, and the words "times" or "factor" refer to multiplication.
find the taylor polynomials p1, ..., p4 centered at a0 for f(x).
Answers
The Taylor polynomials P1, P2, P3, and P4 centered at a0 for f(x) are given as:P1(x) = 1P2(x) = 1 - x²/2!P3(x) = 1 - x²/2! + x⁴/4!P4(x) = 1 - x²/2! + x⁴/4! - x⁶/6!
We will apply the Taylor's theorem formula, which is supplied as follows, to determine the Taylor polynomials P1, P2, P3, and P4 centred at a0 for f(x) in the given question:f'(a)(x-a)/1 = f(x) = f(a) + f'(a)! + f''(a)(x-a)²/2! + ... + fⁿ(a)(x-a)ⁿ/n!We have f(0) = 1f'(0) = 0f''(0) = -1f'''(0) = 0f4(0) = 1 for f(x) = cos(x) at x = 0.We can get the following polynomial expressions by using these values in the Taylor's theorem formula:P1(x) = 1P2(x) = 1 - x²/2!P3(x) = 1 - x²/2! + x⁴/4!P4(x) = 1 - x²/2! + x⁴/4! - x⁶/6!Consequently, the Taylor polynomials P1, P2, P3, and P4 for f(x) are provided as follows:P1(x) = 1P2(x) = 1 - x²/2!P3(x) = 1 - x²/2! + x⁴/4!P4(x) = 1 - x²/2! + x⁴/4! - x⁶/6!
To know more about Taylor polynomials Visit:
https://brainly.com/question/30481013
#SPJ11
yes or no??
math workk

Answers
Answer:
Yes, and if you need extra help try yay math
Step-by-step explanation:
15 lb 7 oz - 6 lb 8 oz =
8 lb 15 oz
Answers
Because 1 lb = 16 oz, we are unable to convert 10 oz to pounds. So, 8.9 ounces is the right response.
what is solution ?a method and otherwise activity for finding the solution; an explanation of the solution. a set of possible values for only a variable that satisfy an equation, specifically Any value of both a variable that makes left Left Hand Side (LHS) or the Dominant Top Left (RHS) of something similar to the equation equal is the solution of the equation. Analyzing an algebraic problem entails locating its solution or solutions. As a fraction of the solute in the solvent, one way to indicate the concentration in the solution. One of two extra approaches for measuring solute concentration is the ratio of the solute's mass to the mass of a solution, also known as the fraction of the solute's bulk here.
given
First, put both into ounces. (1lb = 16oz)
100 ounces equal 6 lbs 4 oz.
5 pounds, 10 ounces are equal to 90 ounces.
Next, subtract.
8.9375 pounds
Because 1 lb = 16 oz, we are unable to convert 10 oz to pounds. So, 8.9 ounces is the right response.
To know more about solution visit :-
https://brainly.com/question/16989201
#SPJ1
Need help with this

Answers
Answer:
probability
Step-by-step explanation:
pls mark me as brainlist
3. You set up a makeshift greenhouse by leaning a square pane of glass against your house. The glass is 4.5 ft long, and it makes a 30° angle with the ground. How much horizontal distance between your house and the glass is there to grow plants? Round to the nearest inch.
Answers
The horizontal distance between the house and the glass to grow plants is approximately 31 inches (rounded to the nearest inch).Note: One foot is equal to 12 inches.
The solution for the given problem is as follows:Given:Length of the square pane of glass, l
= 4.5 ft
Angle that the glass makes with the ground, θ = 30°We have to find the horizontal distance between the house and the glass. This distance is shown by the blue line in the diagram. Let's assume that the distance is x ft.Using trigonometry, we know that tan θ = opposite/hypotenuse or
tan θ
= x/ltan 30°
= x/4.5
= 0.5774⇒ x
= tan 30° × 4.5
= 0.5774 × 4.5
= 2.598 ft
Converting this to inches, we get:
x
= 2.598 × 12
= 31.176 inches ≈ 31 inches.
The horizontal distance between the house and the glass to grow plants is approximately 31 inches (rounded to the nearest inch).Note: One foot is equal to 12 inches.
To know more about horizontal visit:
https://brainly.com/question/29019854
#SPJ11
A flower shop sells 21 different bouquets and multiple different styles of vase. Which are the possible numbers for the total number of combinations of bouquet and vase?
Answers
Prove that if f is differentiable at a, then |f| is also differentiable at a, provided that f(a)≠0
Answers
If a function f is differentiable at a point a and f(a) is not equal to zero, then the absolute value function |f| is also differentiable at that point.
The proof involves considering two cases based on the sign of f(a) and showing that the limit of the difference quotient exists for |f| at point a in both cases. However, it is important to note that |f| is not differentiable at the point where f(a) equals zero.
To prove that if f is differentiable at a, then |f| is also differentiable at a, provided that f(a) ≠ 0, we need to show that the limit of the difference quotient exists for |f| at point a.
Let's consider the function g(x) = |x|. The absolute value function is defined as follows:
g(x) = {
x if x ≥ 0,
-x if x < 0.
Since f(a) ≠ 0, we can conclude that f(a) is either positive or negative. Let's consider two cases:
Case 1: f(a) > 0
In this case, we have g(f(a)) = f(a). Since f is differentiable at a, the limit of the difference quotient exists for f at point a:
lim (x→a) [(f(x) - f(a)) / (x - a)] = f'(a).
Taking the absolute value of both sides, we have:
lim (x→a) |(f(x) - f(a)) / (x - a)| = |f'(a)|.
Since |g(f(x)) - g(f(a))| / |x - a| = |(f(x) - f(a)) / (x - a)| for f(a) > 0, the limit on the left-hand side is equal to the limit on the right-hand side, which means |f| is differentiable at a when f(a) > 0.
Case 2: f(a) < 0
In this case, we have g(f(a)) = -f(a). Similarly, we can use the same reasoning as in Case 1 and conclude that |f| is differentiable at a when f(a) < 0.
Since we have covered both cases, we can conclude that if f is differentiable at a and f(a) ≠ 0, then |f| is also differentiable at a.
Note: It's worth mentioning that at the point where f(a) = 0, |f| is not differentiable. The proof above is valid when f(a) ≠ 0.
To know more about differentiable refer to-
https://brainly.com/question/13958985
#SPJ11
how to know if a function has a vertical asymptote
Answers
To determine if a function has a vertical asymptote, you need to consider its behavior as the input approaches certain values.
A vertical asymptote occurs when the function approaches positive or negative infinity as the input approaches a specific value. Here's how you can determine if a function has a vertical asymptote:
Check for restrictions in the domain: Look for values of the input variable where the function is undefined or has a division by zero. These can indicate potential vertical asymptotes.
Evaluate the limit as the input approaches the suspected values: Calculate the limit of the function as the input approaches the suspected values from both sides (approaching from the left and right). If the limit approaches positive or negative infinity, a vertical asymptote exists at that value.
For example, if a rational function has a denominator that becomes zero at a certain value, such as x = 2, evaluate the limits of the function as x approaches 2 from the left and right. If the limits are positive or negative infinity, then there is a vertical asymptote at x = 2.
In summary, to determine if a function has a vertical asymptote, check for restrictions in the domain and evaluate the limits as the input approaches suspected values. If the limits approach positive or negative infinity, there is a vertical asymptote at that value.
know more about vertical asymptote.
https://brainly.com/question/29260395
#SPJ11
Please solve question 5/160.
5/159 has been uploaded as well for reference. Thanks!
\( 5 / 160 \) Repeat Prob. \( 5 / 159 \), but do not use the approximation of a parabolic cable. Compare your results with the printed answers for Prob. 5/159.
/159 A cable weighing 25 newtons per me
Answers
The sag in the cable for problem 5/160 is approximately 24.4 meters.
To solve the problem of finding the sag in a cable, we can use the catenary equation. The equation is given by:
y = a cosh(x/a)
For problem 5/159, we were given a cable weighing 25 N/m and spanning a distance of 160 m. We can find the tension in the cable by using the formula:
T = wL/2
Substituting in our values, we get:
T = (25 N/m)(160 m)/2 = 2000 N
Now we can solve for a by using the formula:
a = T/(w*g)
where g is the acceleration due to gravity. Substituting in our values, we get:
a = (2000 N)/((25 N/m)*9.81 m/s^2) ≈ 8.13 m
Finally, we can find the sag at the midpoint of the cable (x = L/2) by plugging into the catenary equation:
y = a cosh(x/a) = (8.13 m) cosh(80 m/8.13 m) ≈ 24.6 m
Therefore, the sag in the cable is approximately 24.6 meters.
For problem 5/160, we are given a similar situation but with a shorter span of 159 meters. Using the same method as above, we find that:
T = (25 N/m)(159 m)/2 = 1987.5 N
a = (1987.5 N)/((25 N/m)*9.81 m/s^2) ≈ 8.06 m
y = a cosh(x/a) = (8.06 m) cosh(79.5 m/8.06 m) ≈ 24.4 m
Therefore, the value obtained is approximately 24.4 m.
To know more about acceleration refer here:
https://brainly.com/question/30499732#
#SPJ11
A stagnant pool of water is the perfect breeding place for mosquitoes. If the rate of population growth from breeding is given by b(t) = 9e + 2t where t is days, and at t = the population is 340, how many mosquitoes are added to the population by day 4? Round your answer to the nearest whole number.
Answers
60 mosquitoes are added to the population by day 4.
A stagnant pool of water provides a favorable environment for the breeding of mosquitoes.
The rate of population growth from breeding is given by b(t) = 9e + 2t, where t is measured in days.
If the population is 340 at t = 0, the problem asks us to find the number of mosquitoes added to the population by day 4. We can solve the problem using the following steps:
First, we need to calculate the population at day 4.
To do that, we need to substitute t = 4 in the given formula for b(t).
Therefore, b(4) = 9e + 2(4) = 9e + 8
Next, we can find the population at day 4 by adding the population at t = 0 to the number of mosquitoes added to the population between t = 0 and t = 4.
Therefore ,population at day 4 = 340 + b(4) = 340 + 9e + 8 = 348 + 9e
Now, we can find the number of mosquitoes added to the population by day 4 by subtracting the population at t = 0 from the population at day 4.
Therefore, number of mosquitoes added to the population by day 4 = population at day 4 - population at t = 0= 348 + 9e - 340= 8 + 9e
Finally, we can round our answer to the nearest whole number.
Since e is approximately 2.71828, we can substitute this value in the formula for the number of mosquitoes added to the population by day 4 and round our answer.
Therefore, number of mosquitoes added to the population by day 4 ≈ 8 + 9(2.71828) ≈ 60 (rounded to the nearest whole number).
In summary, 60 mosquitoes are added to the population by day 4.
To know more about rate of population growth, click here
https://brainly.com/question/14570878
#SPJ11
Show that the trajectory of an object thrown at certain angle with the horizontal is a parabola.
Answers
The equation of the trajectory which can be described using the equations for projectile motion is; y(t) = x·tan(θ) - g·x²/(2·v₀²·cos²(θ)), which is a quadratic equation with a path of a parabola
What is projectile motion?Projectile motion is the motion of an object that is projected in the air under the influence of gravitational attraction.
Let θ represent the angle at which the path of the object makes with the horizontal, and let v₀ represent the velocity of the object. The path of the object can be described using the equations of the motion of a projectile, as follows;
Horizontal component of the velocity, v₀ₓ = v₀ × cos(θ)
Vertical component of the velocity, \(v_{0y}\) = v₀ × sin(θ)
The horizontal motion of the object is therefore;
x(t) = v₀ₓ × t = v₀ × cos(θ) × t
The vertical motion which is under the influence of gravity is; y(t) = \(v_{0y}\) × t - (1/2) × g × t²
v₀ × sin(θ) × t - (1/2) × g × t²
The horizontal component indicates that we get;
t = x/(v₀ × cos(θ))
Plugging in the above expression for t into the equation for y(t), we get;
y(t) = \(v_{0y}\) × t - (1/2) × g × t² = \(v_{0y}\) × x/(v₀×cos(θ)) - (1/2) × g × (x/(v₀×cos(θ)))²
\(v_{0y}\) × x/(v₀×cos(θ)) - (1/2) × g × (x/(v₀×cos(θ)))² = (v₀ × sin(θ)) × x/(v₀×cos(θ)) - (1/2) × g × (x/(v₀×cos(θ)))²
(v₀ × sin(θ)) × x/(v₀×cos(θ)) - (1/2) × g × (x/(v₀×cos(θ)))² = x·tan(θ) - g·x²/(2·v₀×cos(θ))²
The equation, y = x·tan(θ) - g·x²/(2·v₀×cos(θ))², is a quadratic equation, which is an equation of a parabola, therefore, the trajectory of an object thrown at an angle to the horizontal is a parabola.
Learn more on projectile motion here: https://brainly.com/question/29583484
#SPJ4
the numbers from $1$ to $150$, inclusive, are placed in a bag and a number is randomly selected from the bag. what is the probability it is neither a perfect square nor a perfect cube? express your answer as a common fraction.
Answers
The required probability is \(\frac{1}{10}\).
This problem is related to probability.
First we have to calculate the number of outcomes and then the number of favorable outcomes.
In this case the numbers are from 1 to 150.
First we have to find the numbers which are perfect square between 1 to 150= {1,4,9,16,25,36,49,64,81,100,121,144}
Now we have to find the numbers which are perfect cube other than those which came in square={8,27,125}
Here the number of favorable outcome is 150 minus number of elements in set of perfect square and perfect cube.
Now the probability of the required problem is = \(\frac{15}{150}\)
= \(\frac{1}{10}\)
To learn more about probability visit the link:
https://brainly.com/question/11234923
#SPJ4
i need help asap please :)

Answers
Answer:
i cant see what u attached please reupload
Step-by-step explanation:
D. 45,000 ft,²
As per the scale given,
1 in. = 15 ft.
10 in. = 10×15 ft. = 150 ft.
20 in. = 20×15 ft. = 300 ft.
So, area = 150 ft. × 300 ft. = 45,000 ft.²
Help!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
read the co ordinates of the curve in the graph
2x-5y=20
What is y and what is x
Answers
Answer:
x=10 and y=4
Im not sure if this is correct but I looked it up and it said it was right
Answer:
x = 5/2y + 10y = 2/5x - 4(if you're looking for intercepts then: x = 10, y = -4)
Step-by-step explanation:
\(\sf{2x - 5y = 20\)
\(\sf{Finding~x:\)
\(2x - 5y = 20\)
\(+ 5y = + 5y\)
↪ 2x = 5y + 20
\(\frac{2x}{2} = \frac{5y}{2} + \frac{20}{2}\)
x = 5/2y + 10\(\sf{Finding~y:}\)
\(2x - 5y = 20\)
\(-2x~ = ~~~~-2x\)
↪ -5y = -2x + 20
\(\frac{-5y}{-5} = \frac{-2x}{-5} + \frac{20}{-5}\)
y = 2/5x - 4--------------------
Hope this helps!
Someone could help me with problem 3-76 (b) pls
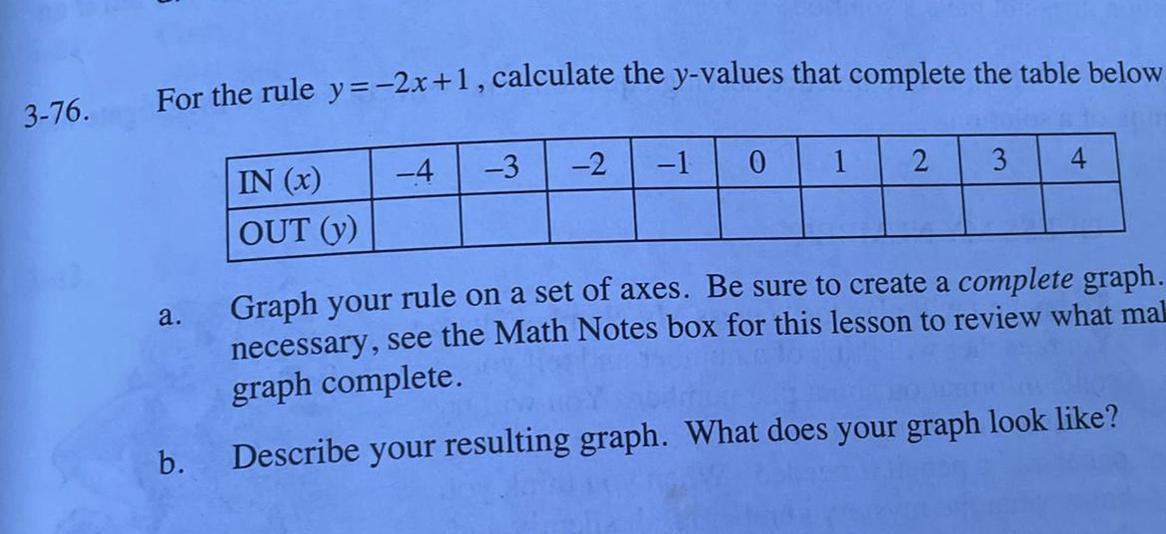
Answers
Answer:
ok so you see the equation at the top... you are going to "plug in" the number in the "in" row to get the "out number
Step-by-step explanation:
example
in: 4
-2(-4)+1
8+1
9
so for the out row under -4 you would put 9
-2(-3)+1
6+1
7
so for the out row under 3 you would put 7
Answer:
...
Step-by-step explanation:


Use polar coordinates to calculate the area of the region. R = {(x, y) | x2 + y2 ≤ 25, x ≥ 4}
Answers
The area of the region R = {(x, y) | x² + y² ≤ 25, x ≥ 4} using polar coordinates is 7π square units.
To calculate the area, first, we need to convert the given equations into polar coordinates. The equation x² + y² ≤ 25 becomes r² ≤ 25, which simplifies to 0 ≤ r ≤ 5. The equation x ≥ 4 can be written as r*cos(θ) ≥ 4. Solving for θ, we get 0 ≤ θ ≤ 2π/3 and 4π/3 ≤ θ ≤ 2π.
Now, use the polar area formula: A = 0.5 * ∫(r² dθ). Integrate r²/2 from 0 to 2π/3 and from 4π/3 to 2π, then multiply by the limits' difference. Finally, add the two areas to find the total area of the region, which is 7π square units.
To know more about polar coordinates click on below link:
https://brainly.com/question/11657509#
#SPJ11
Find x. Perimeter.
What is the value of x?
What is the perimeter of this triangle?

Answers
Step-by-step explanation:
the distance of a vertex on the 2 outgoing sides to the touching points with the inscribed circle is the same for both sides.
and that applies to all 3 vertexes.
so, we know for the top left vertex the distance to both touching points is 4.
that means the distance to the touching points from the bottom left vertex is 7-4 = 3.
and that means that the distance to the touching points from the bottom right vertex is 16-3 = 13.
so, x = 13
it is the distance to one of the touching points for the bottom right vertex.
and the perimeter of the triangle is therefore
7 + 16 + (13 + 4) = 40