Standard form of y=(X+3)^2-10
Answers
Related Questions
In this box-and-whisker plot, what is the maximum
value of the data?
53
56
Ages of People
42 44 46 48 50 52 54 56 58 60 62 54 56 58 70
60
0 0
68

Answers
Answer:
68 is the maximum
Step-by-step explanation:
look at the greatest number
First line joins ordered pairs negative 4, 3 and 2, negative 3. Second line joins negative 4, negative 3 and 2, 3. Part A shaded above first and second line. Part B shaded below first line and above second line. Part C shaded below first and second lines. Part D shaded above first line and below second line. Which part of the graph best represents the solution set to the system of inequalities y ≥ x + 1 and y + x ≤ −1? Part A Part B Part C Part D Question 3(Multiple Choice Worth 5 points) (05.05 MC) Two systems of equations are shown below: System A System B 2x + y = 5 −10x + 19y = −1 −4x + 6y = −2 −4x + 6y = −2 Which of the following statements is correct about the two systems of equations? They will have the same solutions because the first equation of System B is obtained by adding the first equation of System A to 2 times the second equation of System A. They will have the same solution because the first equation of System B is obtained by adding the first equation of System A to 3 times the second equation of System A. The value of x for System B will be −5 times the value of x for System A because the coefficient of x in the first equation of System B is −5 times the coefficient of x in the first equation of System A. The value of x for System A will be equal to the value of y for System B because the first equation of System B is obtained by adding −12 to the first equation of System A and the second equations are identical. Question 4(Multiple Choice Worth 5 points) (05.06 LC) To which graph does the point (−1, −4) belong? y ≤ −x + 4 y ≤ −x − 6 y ≤ 2x − 3 y ≤ 5x − 1 Question 5(Multiple Choice Worth 5 points) (06.04 MC) What is the equation of the graph below? A graph shows a parabola that opens up and crosses the x axis at negative two and negative four. y = − (x − 3)2 + 1 y = − (x + 3)2 + 1 y = (x − 3)2 − 1 y = (x + 3)2 − 1 Question 6 (Fill-In-The-Blank Worth 5 points) (06.04 MC) A ball is thrown upward from the top of a building. The function below
Answers
The part that represents the solution to the inequality will be Part B shaded below first line and above second line.
How to depict the inequality?From the information given, the equation of the first line will be:
y - 3 = (-3 - 3/2 + 4)(x + 4)
y - 3 = -1(x + 4)
y + x = -4 + 3
x + y = -1
The equation of the second line will be:
y + 3 = -1(x + 4)
y = x + 4 - 3
y = x + 1
This is plotted on the graph attached.
From the systems of equations, the statement that is correct about the two systems of equations is that They will have the same solution because the first equation of System B is obtained by adding the first equation of System A to 3 times the second equation of System A.
Learn more about inequalities on:
brainly.com/question/12215820
#SPJ1

Use the following cell phone airport data speeds (Mbps) from a particular network. Find the percentile corresponding to the data speed 4.9 Mbps.
0.2 0.8 2.3 6.4 12.3 0.2 0.8 2.3 6.9 12.7 0.2 0.8 2.6 7.5 12.9 0.3 0.9 2.8 7.9 13.8
0.6 1.5 0.1 0.7 2.2 6.1 12.1 0.6 1.9 5.5 11.9 27.5 0.6 1.7 3.3 8.3 13.8 1.3 3.5 9.8
14.6 10.1 14.7 11.8 14.8
Answers
Answer:
Thus percentile lies between 53.3% and 55.6 %
Step-by-step explanation:
First we arrange the data in ascending order . Then find the number of the values corresponding to the given value. Then equate it with the number of observations and x and then multiply it to get the percentile. n= P/100 *N
where n is the ordinal rank of the given value
N is the number of values in ascending order.
The data in ascending order is
0.1 0.2 0.2 0.2 0.3 0.6 0.6 0.6 0.7 0.8 0.8 0.8 0.9 1.3
1.5 1.7 1.9 2.2 2.3 2.3 2.6 2.8 3.3 3.5 5.5 6.1 6.4 6.9 7.5 7.9 8.3 9.8 10.1 11.8 11.9 12.1 12.3 12.7 12.9 13.8 13.8 14.6 14.7 14.8 27.5
Number of observation = 45
4.9 lies between 3.3 and 5.5
x*n = 24 observation x*n = 25 observation
x*45= 24 x*45= 25
x= 0.533 x= 0.556
Thus percentile lies between 53.3% and 55.6 %
Help me please with my IXL GEOMETRY
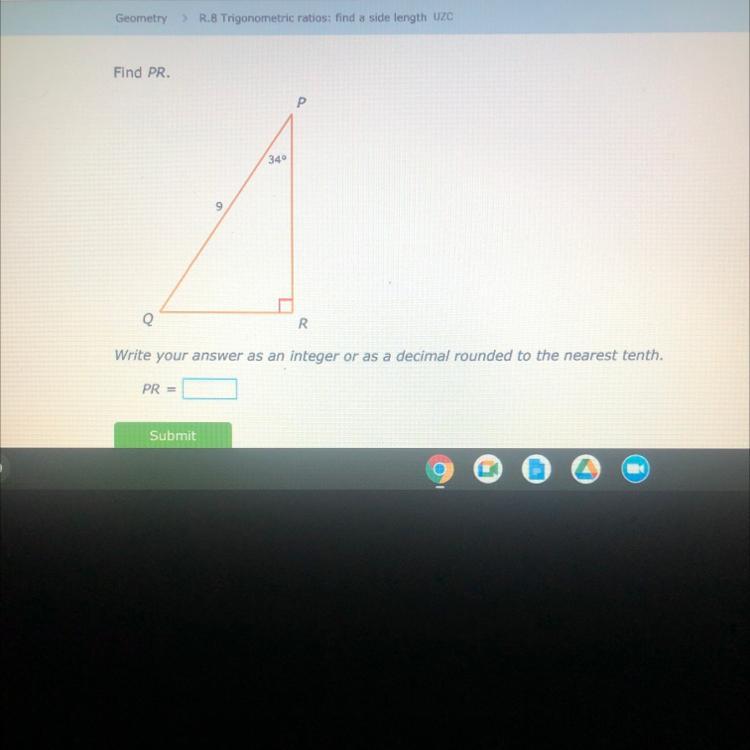
Answers
Answer:
7.5
Step-by-step explanation:
hey hope this helps and is right

Which is equivalent to 80 Superscript one-fourth x? (StartFraction 80 Over 4 EndFraction) Superscript x RootIndex 4 StartRoot 80 EndRoot Superscript x RootIndex x StartRoot 80 EndRoot Superscript 4 (StartFraction 80 Over x EndFraction) Superscript 4
whoever can answer this gets brainliest
Answers
The expression that is equivalent to \(80^{(1/4}\) * x is \(80^{4/x}\)
How to calculate the valueTo determine the equivalent expression to \(80^{1/4}\) * x, let's analyze each option:
\(80/4^{x}\)
This expression simplifies to \(20^{x}\), but it is not equivalent to the original expression.
Applying the power of a power rule, this expression simplifies to \(80^{x/4}\) , which is not equivalent to the original expression.
\(80/x^{4}\)
This expression can be simplified as \(80^{4 x^{4} }\) , which is not equivalent to the original expression.
Therefore, the expression that is option d.
Learn more about expressions on
https://brainly.com/question/723406
#SPJ1
Find tan j and tan k. Write each as a fraction in simplest form and as a decimal rounded to hour places

Answers
Answer:
Step-by-step explanation:
tan j= 24/32
= 3/4
=0.75
tan k= 32/24
= 4/3
=1.3333
Given vectors u = (-2, 3) and v = (-6, 9), what is the measure of the angle between u and v?
0°
86°
91°
180°
Answers
Answer:
A: 0 degrees
Step-by-step explanation:
(-2,3) and (-6,9) have the same slope and are both located in the second quadrant.
The angle between given vectors is 0°. So, option A is correct.
Important information:
The given vertors are u = (-2, 3) and v = (-6, 9).Angle between two vectors:Two vectors \(v_1\) and \(v_2\) are parallel if:
\(v_1=kv_2\)
Where, k is a constant.
\(3u=3\times (-2,3)\)
\(3u=(3\times (-2),3\times 3)\)
\(3u=(-6,9)\)
\(3u=v\)
It means u and v are parallel vectors and the angle between parallel vectors is always 0.
Therefore, the correct option is A.
Find out more about 'Angle between two vectors' here:
https://brainly.com/question/11044032
please help me answer this question thank you

Answers
Answer:
A
Step-by-step explanation:
The organic garden at a restaurant is rectangular in shape and has a perimeter of 84 feet. If the length of the garden is 24 ft longer than the width of the garden what is the area of the garden in sq ft
Answers
Answer:
297 square feet
Step-by-step explanation:
Let w represent the width of the garden.
Since the length is 24 ft longer than the width, it can be represented by w + 24.
Use the perimeter formula, p = 2l + 2w. Plug in the perimeter and w + 24 as l, then solve for w:
p = 2l + 2w
84 = 2(w + 24) + 2w
84 = 2w + 48 + 2w
84 = 4w + 48
36 = 4w
9 = w
So, the width is 9 ft. Add 24 to this to find the length:
24 + 9 = 33
So, the length is 33 ft.
Find the area of the garden with the formula A = lw:
A = lw
A = (33)(9)
A = 297
The area of the garden is 297 square feet.
expand the square of a binomial (r-q)^2
Answers
Answer:
Step-by-step explanation:
Either memorize these two formulas, or derive them through multiplying r - q by r - q.
(r - q)^2 = r^2 - 2qr + q^2, and
(r + q)^2 = r^2 + 2qr + q^2 This is the square of the binomial (r + q).
Simplify your answer as much as possible.

Answers
By using the substitution method, we will see that the value of y is 23.
How to solve the system of equations?Here we have a system of linear equations, the system is:
y - x = 11
x = 12
The second equation is trivial, it just gives the value of x. Then we can use the substitution method and replace it in the first equation, then we will get:
y - 12 = 11
Now we can solve this for y, we will get:
y = 11 + 12
y = 23
That is the value of y.
LEarn moer about systems of equations at:
https://brainly.com/question/13729904
#SPJ1
HELPPP Enter the average exam grade of students who studied, followed by the average exam grade of the students who did not study, using two significant figures, separated by a comma

Answers
The average value of exam grade of students who studies is 92 and students those who did not studied is 68.
What is the average?We have the following information for this case:
Students those who studied:
Exam grade: 94 96 90 88 88 100 78 95 97 94
The sample mean is calculated using the formula:
X = Σxi/n
If we replace the given values, we get:
X = (94 + 96 + 90 + 88 + 88 + 100 + 78 + 95 + 97 + 94)/10
= 920 / 10
= 92
Students those who did not study is :
Exam grade = 64 73 71 64 56 49 89 67 76 71 64 56 49 89 67 76 71
The sample mean is calculated using the formula:
X = Σxi/n
By substituting we get:
X= 64 + 73 + 71 + 64 + 56 + 49 + 89 + 67 + 76 + 71 + 64 + 56 + 49 + 89+ 67 + 76 +71
= 680 / 10
= 68
To learn more about average refer to :
https://brainly.com/question/30066005
#SPJ1
PLEASEEEEE HELP MEEEEEE

Answers
Answer:
A) Vector component for the cruise ship: (0, -22)
B) Vector component for the Gulf Stream: (4, 0)
C) Resultant vector: (4, -22)
D) Resultant velocity: Approximately 22.4 mph (rounded to the nearest tenth)
E) Resultant direction: Approximately -80.5 degrees (rounded to the nearest tenth)
Step-by-step explanation:
To solve this problem, we'll consider the velocities of the cruise ship and the Gulf Stream as vectors and calculate their components and resultant vector. Then we'll find the magnitude (resultant velocity) and direction (resultant direction) of the resultant vector.
Given:
Cruise ship velocity (south): 22 mph
Gulf Stream velocity (east): 4 mph
A) Vector component for the cruise ship:
The cruise ship is traveling south, so its velocity vector is (0, -22).
B) Vector component for the Gulf Stream:
The Gulf Stream is flowing east, so its velocity vector is (4, 0).
C) Resultant vector:
To find the resultant vector, we'll add the two velocity vectors together:
Resultant vector = Cruise ship velocity + Gulf Stream velocity
Resultant vector = (0, -22) + (4, 0)
Resultant vector = (0 + 4, -22 + 0)
Resultant vector = (4, -22)
D) Resultant velocity:
The magnitude of the resultant vector gives us the resultant velocity. We can use the Pythagorean theorem to calculate it:
Resultant velocity = sqrt((x-component)^2 + (y-component)^2)
Resultant velocity = sqrt((4)^2 + (-22)^2)
Resultant velocity = sqrt(16 + 484)
Resultant velocity = sqrt(500)
Resultant velocity ≈ 22.4 mph (rounded to the nearest tenth)
E) Resultant direction:
The direction of the resultant vector can be found using trigonometry. We'll use the inverse tangent function (arctan) to find the angle between the resultant vector and the positive x-axis.
Resultant direction = arctan(y-component / x-component)
Resultant direction = arctan(-22 / 4)
Resultant direction ≈ -1.405 radians or -80.5 degrees (rounded to the nearest tenth)
Therefore, the answers are:
A) Vector component for the cruise ship: (0, -22)
B) Vector component for the Gulf Stream: (4, 0)
C) Resultant vector: (4, -22)
D) Resultant velocity: Approximately 22.4 mph (rounded to the nearest tenth)
E) Resultant direction: Approximately -80.5 degrees (rounded to the nearest tenth)
What is 6 [4(-5)^n-1] n=1 equal to
Answers
The value of 6 [4(-5)^n-1] when n is 1 is 24
What is substitution of variable?This simply means replacing a known value for an unknown value in an expression.
For example, 5x²+2 , the value of the expression when x is -2 is solved by substituting -2 for x in the expression.
5x²+2 = 5(-2)² +2
= 5×4 +2
= 20+2
= 22
Similarly, the value of 6 [4(-5)^n-1] when n= 1 can be calculated by substituting 1 for n in the expression.
6 [4(-5)^n-1] = 6(4(-5)^1-1)
= 6(4(5)^0)
= 6 × 4 × 1
= 24
Therefore the value of 6 [4(-5)^n-1] when n= 1 is 24
learn more about substitution of variable from
https://brainly.com/question/26094713
#SPJ1
Given right triangle ABC, where side "c" is the hypotenuse, angle B measures 42 degrees, and side c measures 18 m, find the length of side b.
Answers
The length of side b of the given right angle triangle using law of sines is; b = 12.044 m
How to use the law of sines?The law of sines states that when we divide side "a" by the sine of angle A, it is equal to side "b" divided by the sine of angle B, and also equal to side "c" divided by the sine of angle C
Thus;
a/sin A = b/sin B = c/sinC
The parameters are;
B = 42°
c = 18m
Since c is the hypotenuse, it is the side that will be opposite the right angle and so;
C = 90°
Thus, using sine rule;
c/sinC = b/sin B
18/sin 90 = b/sin 42
b = (18 * sin 42)/1
b = 12.044 m
Read more about law of sines at; https://brainly.com/question/4372174
#SPJ1
Jamarie owns a tomato farm. Each season, she collects about 3,500 tomatoes. This can vary by as many as 425. What is the maximum and minimum number of tomatoes Jamarie can expect to collect?
Answers
Answer:
max-3925 min-3075
Step-by-step explanation:
Answer:
GIVE BRAINLEIST PLZ Max is 3925 Min is 3075
Step-by-step explanation:
6. Find the sum or difference.
(6g - 3) - (4g + 5)
Answers
y = -x2 + 733 + 73x – 520
Answers
x= -3
If only finding Y
y = 213
0=71x+733-520
0=71x+213
-71x=213
x=-3
Value at Risk (VAR) has become a key concept in financial calculations. The VAR of an investment is defined as that value v such that there is only a 1 percent chance that the loss from the investment will be greater than v.
(a) If the gain from an investment is a normal random variable with mean 10 and variance 49 determine the VAR. (IfX is the gain, then ?X is the loss.)
(b) Among a set of investments all of whose gains are normally distributed, show that the one having the smallest VAR is the one having the largest value of mean minus standard deviation*2.33?
Answers
Answer:
Var = 6.31
Step-by-step explanation:
The Value at Risk (VAR)
\(P(X < x_o) = 0.01\)
By using normal distribution
Mean \(\mu\) = 10
Variance = 49
Standard deviation \(\sigma = \sqrt{49 } = 7\)
This implies that:
\(P\Big ( \dfrac{X - \mu}{\sigma } < \dfrac{x_o - \mu }{\sigma}\Big) = 0.01 \\ \\ P\Big ( Z < \dfrac{x_o - \mu }{\sigma}\Big) = 0.01 \\ \\ \dfrac{x_o - \mu }{\sigma} = invNorm(0.01) \\ \\ x_o = \mu + \sigma \times invNorm (0.01)\)
Using the z-table;
\(x_o = 10 + 7 \times (-2.33) \\ \\ x_o = -6.3100\)
Hence, there exist 1% chance that X < -6.31 or the loss from investment is > 6.31
From the calculated value above;
\(V = \mu -\sigma \times 2.33\); Since the result is negative, then it shows that the greater the value(i.e the positive or less negative it is ) the lower is the value of VAR. Thus, the least value of VAR is accepted by the largest value of
\(min( \mu -\sigma \times2.33,0)\)
How can you use Triangle Congruence to solve real-world problems?
Answers
Answer:
Many pairs of triangles designed into a building, for example as roof ends, would be congruent, so the roof beam and the top edges of the walls are horizontal.
ES LA OPERACION DE MOVER LOS EJES COORDENADOS EN EL PLANO COORDENADO A UNA POSICION DIFERENTE, MANTENIENDOLOS PARALELOS A LOS ORIGINALES Y EN EL MISMO SENTIDO
Answers
Put in order from greatest to svllems 12 1/2, 12.09,. 12 2/5,12.8
Answers
Answer:
12.8
12 1/2
12 2/5
12.09
24÷6+2×9 without using a calculator
Answers
Answer:
Step-by-step explanation:
\(24\div 6+2\times 9 =4+18=22\)
÷ and × first followed by + and -. But otherwise work left to right.
Answer: 22
Step-by-step explanation:
1.) Solve using PEMDAS.
Which linear function has the same y-intercept as the one that is represented by the graph?
On a coordinate plane, a line goes through points (3, 4) and (5, 0).
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 3, negative 1, 1, 3. Column 2 is labeled y with entries negative 4, 2, 8, 14.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 4, negative 2, 2, 4. Column 2 is labeled y with entries negative 26, negative 18, negative 2, 6.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 5, negative 3, 3, 5. Column 2 is labeled y with entries negative 15, negative 11, 1, 5.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 6, negative 4, 4, 6. Column 2 is lab
eled y with entries negative 26, negative 14, 34, 46.
Answers
The linear function that has the same y-intercept as the given graph is the equation y = -2x + 10, corresponding to option 3.
To determine the linear function with the same y-intercept as the graph, we need to find the equation of the line passing through the points (3, 4) and (5, 0).
First, let's find the slope of the line using the formula:
slope (m) = (change in y) / (change in x)
m = (0 - 4) / (5 - 3)
m = -4 / 2
m = -2
Now that we have the slope, we can use the point-slope form of a linear equation to find the equation of the line:
y - y1 = m(x - x1)
Using the point (3, 4) as our reference point, we have:
y - 4 = -2(x - 3)
Expanding the equation:
y - 4 = -2x + 6
Simplifying:
y = -2x + 10
Now, let's check the given options to find the linear function with the same y-intercept:
Option 1: The table with x-values (-3, -1, 1, 3) and y-values (-4, 2, 8, 14)
The y-intercept is not the same as the given line. So, this option is not correct.
Option 2: The table with x-values (-4, -2, 2, 4) and y-values (-26, -18, -2, 6)
The y-intercept is not the same as the given line. So, this option is not correct.
Option 3: The table with x-values (-5, -3, 3, 5) and y-values (-15, -11, 1, 5)
The y-intercept is the same as the given line (10). So, this option is correct.
Option 4: The table with x-values (-6, -4, 4, 6) and y-values (-26, -14, 34, 46)
The y-intercept is not the same as the given line. So, this option is not correct.
Therefore, the linear function that has the same y-intercept as the given graph is the equation y = -2x + 10, corresponding to option 3.
for such more question on linear function
https://brainly.com/question/9753782
#SPJ8
Solve using substitution 1.) x+y+2z=-7 / -5z=25 / 3x-3y-6z=32.) 2x+3y-4z=-3 / -x-2y+3z=4 /-x-z=4
Answers
Okay, here we have this:
We need to solve the following system:
x+y+2z=-7 (1)
-5z=25 (2)
3x-3y-6z=3 (3)
First we are going to clear z in (2):
-5z=25
z=-5
Now let's replace z=-5 in (1):
x+y+2z=-7
x+y+2(-5)=-7
x+y-10=-7 (4)
3x-3y-6z=3
3x-3y-6(-5)=3
3x-3y+30=3 (5)
Now let's clear x in (4):
x+y-10=-7
x=-y+3
Let's replace x=-y+3 in (5):
3x-3y+30=3
3(-y+3)-3y+30=3
-6y+39=3
Now, let's clear y:
-6y+39=3
y=(3-39)/-6
y=-36/-6
y=6
And finally we are going to replace y=6 in x=-y+3
x=-y+3
x=-6+3
x=-3
Finally we obtain that the solution of the system is x=-3, y=6 and z=-5.
An employee at a shoe store has observed that taller customers have larger shoe sizes than customers who are shorter. She knows that shoe sizes are based on foot length, so she hypothesizes: Compared with shorter people, taller people have longer feet. Look for patterns in the data. Describe any patterns you find.
Answers
Answer:
hello some information related to your question is missing
answer : The pattern discovered supports the hypothesis that taller customers have larger shoe sizes but with some exceptions and this exceptions are ; at Height 5ft 10 inches two people are seen to have different shoe sizes i.e. Eduardo with shoe size : 10.25 inches and Susan with shoe size : 10inches. another exception from the pattern is Lily having a height of 5 ft and shoe length of 9 inches .
Step-by-step explanation:
From the data given the pattern discovered supports the hypothesis that taller customers have larger shoe sizes but with some exceptions and this exceptions are ; at Height 5ft 10 inches two people are seen to have different shoe sizes i.e. Eduardo with shoe size : 10.25 inches and Susan with shoe size : 10inches. another exception from the pattern is Lily having a height of 5 ft and shoe length of 9 inches .


what is the value of d (over-bar) for the following set of difference scores? scores: 3, -8, 6, -4, -2
a. -1
b. -3.4
c. -4
d. 23
Answers
The value of d-bar for the set of difference scores is -2.5.
To find the value of d-bar for the set of difference scores, we first need to calculate the differences. Taking each score and subtracting the one before it, we get:
= -8 - 3 = -11
= 6 - (-8) = 14
= -4 - 6 = -10
= -2 - (-4) = 2
differences = {-11, 14, -10, 2}
Next, we need to calculate the mean of these differences:
d-bar = (sum of differences) / (number of differences)
= (-11 + 14 - 10 + 2) / 4
= -5 / 2
Therefore, the value of d-bar for the set of difference scores is -2.5.
To know more about Mean:
https://brainly.com/question/30112112
#SPJ4
what are exchange rates?
Answers
Answer:
Step-by-step explanation:
Exchange rates are the rates at which one currency can be exchanged for another currency. They represent the value of one currency relative to another currency.
Camillo needs 2,400 oz of jelly for the food challenge. If 48 oz of jelly cost $3.84, how much will Camillo spend on jelly? Explain how you can find your answer
Answers
Answer:
She'll spend 192 because 2400 divided by 48 equals 50 times that by 3.84 which will give you 192.
Answer:
14 packages
Step-by-step explanation:
all you would do is 2,400 divide 48 to get 50 then do 50 divide by 3.84 to get 13.020 then you would round so you need about 14 packages.
f(x) = -×-3
find f(-4)
Answers
Answer:
Hey there!
Original function: f(x)=-x-3
Substituting -4: f(-4)=4-3
Simplify: f(-4)=1
Let me know if this helps :)
F(x) = -x - 3
F(-4)
Replace x with -4 and solve:
F(-4) = -(-4) -3
-(-4) = positive 4
So you have 4-3
4-3 = 1
F(-4) = 1