Square: if AC =26, find BC
Answers
BC is equal to 24cm.Now, by applying the Pythagoras theorem i.e. in a right-angled triangle, the square of the hypotenuse is equal to the sum of the square of the other two sides, we can find BC.
Find BC ?
So, we can apply the Pythagoras theorem here, if it is right-angled at C then the side opposite to C will be the hypotenuse of the triangle that is AB = 25 cm, and the other two sides are AC = 7 cm and BC.
AB = 25 cm, AC = 7 cm and BC =?
In triangle ACB, By Pythagoras theorem, (Hypotenuse)2 = (Perpendicular)2 + (Base)2
AB)2 = (AC)2 + (BC)2
(25)2 = (7)2 + (BC)2
625 = 49 + (BC)2
(BC)2 = 625 – 49
(BC)2 = 576
BC = 24 cm
Thus, BC is equal to 24cm
To learn more about Pythagoras theorem refer
https://brainly.com/question/343682
#SPJ1
Related Questions
please help lots of points

Answers
Answer:
see below
Step-by-step explanation:
The area is given by
A = l*w
A = (4x-1) ( 3x+6)
FOIL
first 4x*3x =12x^2
outer 6*4x = 24x
inner -1*3x = -3x
last -1 *6 = -6
Add together
12x^2 +24x-3x-6
12x^2 +21x-6
Answer:
The area is given by
A = l*w
A = (4x-1) ( 3x+6)
first 4x*3x =12x^2
outer 6*4x = 24x
inner -1*3x = -3x
last -1 *6 = -6
Add together
12x^2 +24x-3x-6
12x^2 +21x-6
Evaluate the integral. (Use C for the constant of integration.) 3x cos(8x) dx
Answers
To evaluate the integral ∫3x cos(8x) dx, we need to find an antiderivative of the given function. The result will be expressed in terms of x and may include a constant of integration, denoted by C.
To evaluate the integral, we can use integration by parts, which is a technique based on the product rule for differentiation. Let's consider the function u = 3x and dv = cos(8x) dx. Taking the derivative of u, we get du = 3 dx, and integrating dv, we obtain v = (1/8) sin(8x).
Using the formula for integration by parts: ∫u dv = uv - ∫v du, we can substitute the values into the formula:
∫3x cos(8x) dx = (3x)(1/8) sin(8x) - ∫(1/8) sin(8x) (3 dx)
Simplifying this expression gives:
(3/8) x sin(8x) - (3/8) ∫sin(8x) dx
Now, integrating ∫sin(8x) dx gives:
(3/8) x sin(8x) + (3/64) cos(8x) + C
Thus, the evaluated integral is:
∫3x cos(8x) dx = (3/8) x sin(8x) + (3/64) cos(8x) + C, where C is the constant of integration.
Learn more about product rule for differentiation here:
https://brainly.com/question/28993079
#SPJ11
Find the volume of the figure

Answers
Answer:
\(800\pi yd^3\)
Step-by-step explanation:
\(A = 10\pi ^2(8)\\= 800\pi yd^3\)
Answer: 2513.27 yd³
Step-by-step explanation:
Volume of a cylinder:
-> This formula means we are finding the area of the base circle and multiplying it be the height
V = πr²h
V = πr²h
V = π(10)²(8)
V ≈ 2513.27 yd³
The volume of the figure is about 2513.27 yd³.
the time needed to complete a final examination in a particular college course is normally distributed with a mean of
Answers
The probability of a student completing the final examination in less than 65 minutes is 13.45%.
The time it takes to complete a final examination in a particular college course is normally distributed with a mean of 77 minutes and a standard deviation of 12 minutes. This can be expressed mathematically as X~N(77, 12).
The probability of a student completing the final examination in less than 65 minutes can be calculated by using the Z-score formula:
Z = (x - μ) / σ
Where x = 65 minutes, μ = 77 minutes, and σ = 12 minutes.
Plugging these values into the formula, we get:
Z = (65 - 77) / 12 = -1.17
Using a Z-score table, we can find the probability of a student completing the final examination in less than 65 minutes, which is equal to 0.1345, or 13.45%. Therefore, the probability of a student completing the final examination in less than 65 minutes is 13.45%.
Learn more about probability here:
brainly.com/question/30034780
#SPJ4
What is 1 bar equal to in kPa?
Answers
So, if you have a pressure measurement of 1 bar, multiplying it by 100 gives you 100 kilopascals.
Converting between different units of pressure, such as bars and kilopascals, is a common task in physics, engineering, and many other fields.
Here's a more detailed explanation: One bar is equivalent to 100 kilopascals (kPa). This means that if you have a pressure measurement in bars, you can convert it to kilopascals by multiplying it by 100.
It's important to note that the conversion factor of 100 is constant, so any value in bars can be easily converted to kilopascals by multiplying by 100.
For example,
if you have a pressure measurement of 2 bars, multiplying it by 100 gives you 200 kilopascals. And if you have a pressure measurement of 0.5 bars, multiplying it by 100 gives you 50 kilopascals.
to know more about bar in kpa refer here
https://brainly.com/question/29503266#
#SPJ11
what is the solution of the inequality below?
y-1≥0
Answers
Answer:
y≥1
Step-by-step explanation:
hello :
y-1≥0
y-1+1≥0+1
y≥1
the probility of alvins mother will server rice with dinner is 0.78 the probilty that she will server carrots is with dinner is 0.30
Answers
The probability of both rice and carrots being served with dinner is 23.4%.
The probability of Alvin's mother serving rice with dinner can be expressed using the formula P(Rice) = 0.78. This means that the probability of Alvin's mother serving rice with dinner is 78%. The probability of Alvin's mother serving carrots with dinner can be expressed using the formula P(Carrots) = 0.30. This means that the probability of Alvin's mother serving carrots with dinner is 30%. To calculate the combined probability of both rice and carrots being served with dinner, we can use the formula P(Rice and Carrots) = P(Rice) * P(Carrots) = 0.78 * 0.30 = 0.2340. This means that the probability of both rice and carrots being served with dinner is 23.4%.
Learn more about probability here:
https://brainly.com/question/11234923
#SPJ4
I need to convert 35° into radian pls help.
Answers
Answer:
\(35\cdot\frac{\pi}{180}=\frac{7}{36}\pi\approx0.611\)Step-by-step explanation:
To convert degrees to radians, we can use the following formula:
\(\text{degrees}\cdot\frac{\pi}{180}=\text{radians}\)Then, for 35 degrees:
\(35\cdot\frac{\pi}{180}=\frac{7}{36}\pi\approx0.611\)The total clockwise moment about a pivot
is 5Nm and the total anti-clockwise
moment is 10Nm. In which direction will
the object turn?
Answers
The direction in which the object will turn is; Anti Clockwise Direction
What is the direction of the moment?If the force acting on a body rotates the body in the clockwise direction with respect to the axis of rotation, then we can say that the moment is called the clockwise moment.
However, if the force rotates the body in the anti-clockwise direction, then it means that the moment is said to be the anti-clockwise moment.
An anticlockwise moment is taken as positive while a clockwise moment is taken as negative.
Thus;
First torque = 5 N.m ( clockwise direction)
Second torque = 10 N.m (anticlockwise direction)
Total torque = 5Nm (Clockwise) + 10Nm N(Anticlockwise)
= -5Nm (Anticlockwise) + 10 Nm (Anticlockwise)
= 5 Nm (Anticlockwise)
Therefore it is clear that object will turn Anticlockwise with 5 Nm torque.
Read more about Moment Direction at; https://brainly.com/question/14839816
#SPJ1
Kabir wants to know the volume of a solid right pyramid with a square base.
Answers
if 60% of a number is 120 and 25% of the same number is 50 find 85% of that number
PLEASE HELP!
CORRECT= BRAINLIEST
Answers
Answer:
85% of 200 = 170
Step-by-step explanation:
Method
Let the number = x
60/100 * x = 120
0.6 x = 120 Divide by 0.6
0.6x/0.6 = 120/0.6
x = 200
25% x = 50 Convert 25% to a fraction
25/100 x = 50
0.25x = 50 Divide by 0.25
0.25x/0.25 = 50/0.25
x = 200
85% 200 = x Change 85% to a fraction
85/100 * 200 = x Multiply 85 and 200 together
17000 /100 = x Divide by 100
170 = x
Answer
85% of 200 = 170
3a+2b=13. 5a-3b=9. simultaneous equations
Answers
Answer:
a=3 , b=2
Step-by-step explanation:
(2a-b-c)³+(2b-c-a)³+(2c-a-b)³ factorise
Answers
Answer:
Sowy but try Mathwa y
Step-by-step explanation:
By using Laplace transform to solve y′′−3y′+4y=0 with y(0)=1 and y′(0)=5, what would the particular solution be?
Answers
The particular solution to the given differential equation with the initial conditions y(0) = 1 and y'(0) = 5 is:
\(y(t) = e^{2t} * (t + e^{-2t})\)
To solve the given differential equation using Laplace transforms, we will first take the Laplace transform of both sides of the equation. The Laplace transform of a derivative is given by:
L{y'(t)} = sY(s) - y(0)
L{y''(t)} = s²Y(s) - sy(0) - y'(0)
Applying the Laplace transform to the given differential equation, we have:
s²Y(s) - sy(0) - y'(0) - 3(sY(s) - y(0)) + 4Y(s) = 0
Simplifying and rearranging the terms, we get:
(s² - 3s + 4)Y(s) - s - 3 + 4 = 0
(s² - 3s + 4)Y(s) - (s - 1) = 0
Dividing both sides by (s² - 3s + 4), we obtain:
Y(s) = (s - 1) / (s² - 3s + 4)
To find the inverse Laplace transform and obtain the particular solution y(t), we need to decompose the right side of the equation into partial fractions. Let's factor the denominator:
s² - 3s + 4 = (s - 1)(s - 3) + 1
Therefore, the decomposition is:
Y(s) = (s - 1) / [(s - 1)(s - 3) + 1]
Now, let's rewrite the decomposition:
Y(s) = (s - 1) / [(s - 1)(s - 3) + 1]
= (s - 1) / [s² - 4s + 3 + 1]
= (s - 1) / [(s - 2)²]
Using the property of the Laplace transform, the inverse Laplace transform of (s - a) / (s - b)² is given by e^(at) * (t + e^(-bt)), where a = 2 and b = 2.
Therefore, the particular solution y(t) is:
\(y(t) = e^{2t} * (t + e^{-2t})\)
Now we can substitute the initial conditions to find the particular solution:
\(y(0) = e^{20} * (0 + e^{-20}) = 1\\y'(0) = 2 * e^{20} * (0 + e^{-20}) + e^{2*0} = 2\)
Thus, the particular solution to the given differential equation with the initial conditions y(0) = 1 and y'(0) = 5 is:
\(y(t) = e^{2t} * (t + e^{-2t})\)
To learn more about Laplace transform visit:
brainly.com/question/30759963
#SPJ11
(a) Show that the vectors u1 = (2, 0, 3), u2 = (−3, 0, 2) and u3 = (0, 7, 0) form an orthogonal basis for R 3 .(b) Write v = (1, 2, 3) as a linear combination of u1 = (2, 0, 3), u2 = (−3, 0, 2) and u3 = (0, 7, 0).
Answers
Main Answer:The linear combination of v = (13/14)u1 + (2/7)u2 + (47/14)u3
Supporting Question and Answer:
How can we express a vector as a linear combination of vectors using a system of equations?
To express a vector as a linear combination of vectors using a system of equations, we need to find the coefficients that multiply each given vector to obtain the desired vector. This can be done by setting up a system of equations, where each equation corresponds to the components of the vectors involved.
Body of the Solution:
(a) To show that the vectors u1 = (2, 0, 3), u2 = (-3, 0, 2), and u3 = (0, 7, 0) form an orthogonal basis for R^3, we need to demonstrate two conditions: orthogonality and linear independence.
Orthogonality: We need to show that each pair of vectors is orthogonal, meaning their dot product is zero.u1 · u2 = (2)(-3) + (0)(0) + (3)(2) = -6 + 0 + 6 = 0
u1 · u3 = (2)(0) + (0)(7) + (3)(0) = 0 + 0 + 0 = 0
u2 · u3 = (-3)(0) + (0)(7) + (2)(0) = 0 + 0 + 0 = 0
Since the dot product of every pair of vectors is zero, they are orthogonal.
2.Linear Independence: We need to show that the vectors u1, u2, and u3 are linearly independent, meaning that no vector can be written as a linear combination of the other vectors.
We can determine linear independence by forming a matrix with the vectors as its columns and performing row operations to check if the matrix can be reduced to the identity matrix.
[A | I] = [u1 | u2 | u3 | I] =
[2 -3 0 | 1 0 0]
[0 0 7 | 0 1 0]
[3 2 0 | 0 0 1]
Performing row operations:
R3 - (3/2)R1 -> R3
R1 <-> R2
[1 0 0 | -3/2 1 0]
[0 1 0 | 0 1 0]
[0 0 7 | 0 0 1]
Since we can obtain the identity matrix on the left side, the vectors u1, u2, and u3 are linearly independent.
Therefore, the vectors u1 = (2, 0, 3), u2 = (-3, 0, 2), and u3 = (0, 7, 0) form an orthogonal basis for R^3.
(b) To write v = (1, 2, 3) as a linear combination of u1, u2, and u3, we need to find the coefficients x, y, and z such that:
v = xu1 + yu2 + z*u3
Substituting the given vectors and coefficients:
(1, 2, 3) = x(2, 0, 3) + y(-3, 0, 2) + z(0, 7, 0)
Simplifying the equation component-wise:
1 = 2x - 3y
2 = 7y
3 = 3x + 2y
From the second equation, we can solve for y:
y = 2/7
Substituting y into the first equation:
1 = 2x - 3(2/7)
1 = 2x - 6/7
7 = 14x - 6
14x = 13
x = 13/14
Substituting the found values of x and y into the third equation
3 = 3(13/14) + 2(2/7)
3 = 39/14 + 4/7
3 = 39/14 + 8/14
3 = 47/14
Therefore, we have determined the values of x, y, and z as follows:
x = 13/14
y = 2/7
z = 47/14
Thus, we can write the vector v = (1, 2, 3) as a linear combination of u1 = (2, 0, 3), u2 = (-3, 0, 2), and u3 = (0, 7, 0) as:
v = (13/14)u1 + (2/7)u2 + (47/14)u3
Therefore, v can be expressed as a linear combination of the given vectors.
Final Answer:Therefore,the linear combination of v = (13/14)u1 + (2/7)u2 + (47/14)u3
To learn more about a vector as a linear combination of vectors using a system of equations from the given link
https://brainly.com/question/30758379
#SPJ4
The linear combination of v = (13/14)u1 + (2/7)u2 + (47/14)u3
To express a vector as a linear combination of vectors using a system of equations, we need to find the coefficients that multiply each given vector to obtain the desired vector. This can be done by setting up a system of equations, where each equation corresponds to the components of the vectors involved.
Body of the Solution:
(a) To show that the vectors u1 = (2, 0, 3), u2 = (-3, 0, 2), and u3 = (0, 7, 0) form an orthogonal basis for R^3, we need to demonstrate two conditions: orthogonality and linear independence.
Orthogonality: We need to show that each pair of vectors is orthogonal, meaning their dot product is zero.
u1 · u2 = (2)(-3) + (0)(0) + (3)(2) = -6 + 0 + 6 = 0
u1 · u3 = (2)(0) + (0)(7) + (3)(0) = 0 + 0 + 0 = 0
u2 · u3 = (-3)(0) + (0)(7) + (2)(0) = 0 + 0 + 0 = 0
Since the dot product of every pair of vectors is zero, they are orthogonal.
2.Linear Independence: We need to show that the vectors u1, u2, and u3 are linearly independent, meaning that no vector can be written as a linear combination of the other vectors.
We can determine linear independence by forming a matrix with the vectors as its columns and performing row operations to check if the matrix can be reduced to the identity matrix.
[A | I] = [u1 | u2 | u3 | I] =
[2 -3 0 | 1 0 0]
[0 0 7 | 0 1 0]
[3 2 0 | 0 0 1]
Performing row operations:
R3 - (3/2)R1 -> R3
R1 <-> R2
[1 0 0 | -3/2 1 0]
[0 1 0 | 0 1 0]
[0 0 7 | 0 0 1]
Since we can obtain the identity matrix on the left side, the vectors u1, u2, and u3 are linearly independent.
Therefore, the vectors u1 = (2, 0, 3), u2 = (-3, 0, 2), and u3 = (0, 7, 0) form an orthogonal basis for R^3.
(b) To write v = (1, 2, 3) as a linear combination of u1, u2, and u3, we need to find the coefficients x, y, and z such that:
v = xu1 + yu2 + z*u3
Substituting the given vectors and coefficients:
(1, 2, 3) = x(2, 0, 3) + y(-3, 0, 2) + z(0, 7, 0)
Simplifying the equation component-wise:
1 = 2x - 3y
2 = 7y
3 = 3x + 2y
From the second equation, we can solve for y:
y = 2/7
Substituting y into the first equation:
1 = 2x - 3(2/7)
1 = 2x - 6/7
7 = 14x - 6
14x = 13
x = 13/14
Substituting the found values of x and y into the third equation
3 = 3(13/14) + 2(2/7)
3 = 39/14 + 4/7
3 = 39/14 + 8/14
3 = 47/14
Therefore, we have determined the values of x, y, and z as follows:
x = 13/14
y = 2/7
z = 47/14
Thus, we can write the vector v = (1, 2, 3) as a linear combination of u1 = (2, 0, 3), u2 = (-3, 0, 2), and u3 = (0, 7, 0) as:
v = (13/14)u1 + (2/7)u2 + (47/14)u3
Therefore, v can be expressed as a linear combination of the given vectors.
Therefore, the linear combination of v = (13/14)u1 + (2/7)u2 + (47/14)u3
Learn more about linear combination
https://brainly.com/question/32297475
#SPJ4
Rewrite one eighteenthx3y + seven eighteenthsxy2 using a common factor.
one thirdxy(6x2 + 7y)
one thirdx2y(6x2 + 9y)
one eighteenthxy(x2 + 7y)
one eighteenthx3y2(y + 7)
Answers
Answer:
C
Step-by-step explanation:
1/18 x³y + 7/18 xy²
1/18 xy (x² + 7y)
What is the surface area of the rectangular prism below?

Answers
The surface area of the rectangular prism is 362 square inches.
What is surface area ?Surface area refers to the total area of all the faces or surfaces of a three-dimensional object. It is measured in square units and is calculated by adding the area of each individual face or surface. The formula for calculating the surface area of different 3D shapes varies depending on the shape, but the basic concept remains the same - adding the areas of all the faces or surfaces that make up the object. Surface area is an important concept in fields such as mathematics, engineering, and physics, and is used in the design and analysis of various structures and objects.
According to given information :To find the surface area of a rectangular prism with length (l) = 16 inches, width (b) = 7 inches, and height (h) = 3 inches, we use the formula:
SA = 2lb + 2lh + 2wh
Substituting the values, we get:
SA = 2(167) + 2(163) + 2(7*3)
SA = 224 + 96 + 42
SA = 362
Therefore, the surface area of the rectangular prism is 362 square inches.
To know more about surface area visit:
https://brainly.com/question/16519513
#SPJ1
PLEASE HELP IM ON A TIME LIMIT :(
In the similarity
transformation of AACB
to AEFD, AACB was dilated by
a scale factor of [?], reflected
across the [ ], and moved
through the translation[ ].
A. 2
B. 1/2
C. 3
D. 1/3
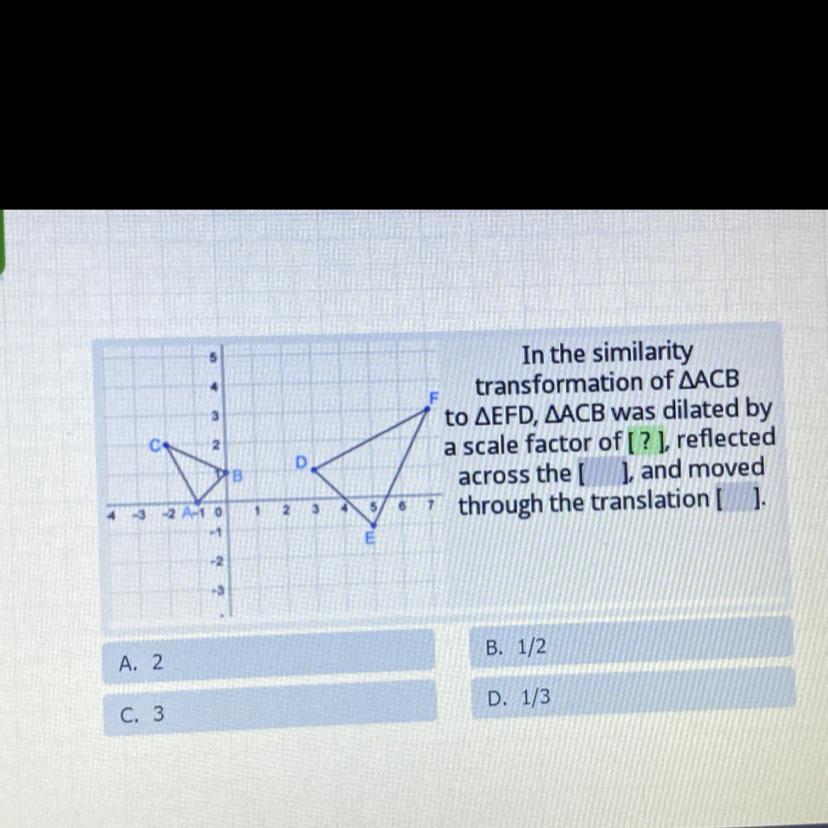
Answers
Answer:
hey hope this helps
Comparing sides AB and DEAB =
\( \sqrt{ {1}^{2} + {1}^{2} } \)
\( = \sqrt{2} \)
DE
\( = \sqrt{ {(3 - 5)}^{2} + {(1 + 1}^{2} } \\ = \sqrt{ {( - 2)}^{2} + {(2)}^{2} } \\ = \sqrt{4 + 4} \\ = \sqrt{8} \\ = 2 \sqrt{2} \)
So DE = 2 × AB
and since the new triangle formed is similar to the original one, their side ratio will be same for all sides.
scale factor = AB/DE
= 2
It's been reflected across the Y-axis
moved thru the translation of 3 units towards the right of positive x- axis
for this let's compare the location of points B and D
For both the y coordinate is same while the x coordinate of B is 0 and that of D is 3
so the triangle has been shifted by 3 units across the positive x axis
What is the value of y?

Answers
Answer (12,5). In this example, the value "5" is the Y Coordinate.
Step-by-step explanation:
The vertical value in a pair of coordinates. How far up or down the point is. The Y Coordinate is always written second in an ordered pair of coordinates (x,y) such as (12,5). In this example, the value "5" is the Y Coordinate.
9514 1404 393
Answer:
y = 24
Step-by-step explanation:
The line marked 'x' is a midline of the triangle, hence half the length of the parallel base line marked '4x-7'. This lets us solve for x and find the lengths of the sides of the triangle.
2x = 4x -7
7 = 2x . . . . . add 7-2x
3.5 = x
Then the horizontal side of the triangle is ...
4x -7 = 4(3.5) -7 = 7
The hypotenuse of the triangle is ...
6x +4 = 6(3.5) +4 = 25
The Pythagorean theorem can be used to find y:
y^2 +7^2 = 25^2
y^2 = 625 -49 = 576
y = √576
y = 24
show that 2x +1 is a factor of 2x3 +5x2+4x+1 and factories completely
Answers
\(\text{According to the factor theorem, if f(b) = 0, then x-b is a factor of f(x).}\\\\\text{Given that,}\\\\f(x) = 2x^3 +5x^2 +4x +1 \\\\f\left(-\dfrac 12 \right) = 2\left( - \dfrac 12 \right)^3 +5 \left( - \dfrac 12 \right)^2 +4 \left( - \dfrac 12 \right) +1 \\\\\\~~~~~~~~~~~~=-2 \cdot \dfrac 18 + 5 \cdot \dfrac 14 -2 +1 \\\\\\~~~~~~~~~~~=\dfrac 54 -\dfrac14 -1\\\\\\~~~~~~~~~~~=\dfrac 44 -1 \\\\\\~~~~~~~~~~~=1-1\\\\\\~~~~~~~~~~~=0\\\\\text{So,}~ 2x +1 ~ \text{is a factor of f(x).}\)
\(\text{Now,}\\\\f(x) = 2x^3 +5x^2 +4x +1 \\\\~~~~~~=2x^3+x^2 +2x^2 +2x +2x+1\\\\~~~~~~=x^2(2x+1) +2x(2x+1) + (2x+1)\\\\~~~~~~=(2x+1)(x^2 +2x +1)\\\\~~~~~~=(2x+1)(x+1)^2\)
I need a answer fast thanks!

Answers
Answer:
Chart:
x y
-6 11
3 5
15 -3
-12 15
Step-by-step explanation:
The only things you can plug in are the domain {-12, -6, 3, 15}
Plug in the domain into equation to find y.
-6 :
y = -2/3 (-6) +7
y = +47
y=11
(-6,11)
3:
y = -2/3 (3) +7
y = -2 +7
y = 5
(3, 5)
15:
y = -2/3 (15) +7
y = -10 +7
y = -3
(15 , -3)
-12:
y = -2/3 (-12) +7
y = 8 + 7
y= 15
(-12,15)
Answer:
1) 11
2) 3
3) -3
4) -12
Step-by-step explanation:
eq(1):
\(y = \frac{-2}{3} x + 7\\\\y - 7 = \frac{-2}{3} x\\\\x = (y - 7)\frac{-3}{2} \\\\x = (7-y)\frac{3}{2} ---eq(2)\)
1) x = -6
sub in eq(1)
\(y = \frac{-2}{3} (-6) + 7\\\\y = \frac{12}{3} + 7\\\\y = 4+7\\\\y = 11\)
2) y = 5
sub in eq(2)
\(x = (7-5)\frac{3}{2} \\\\x = 3\)
3) x = 15
sub in eq(1)
\(y = \frac{-2}{3} 15 + 7\\\\y = \frac{-30}{3} +7\\\\y = -10 + 7\\\\y = -3\)
4)
sub in eq(2)
\(x = (7-15)\frac{3}{2} \\\\x = -8\frac{3}{2}\\ \\x = -12\)
Can anyone write the equation of this graph?


Answers
The translated absolute value function graphed is defined as follows:
y = |x - 3| + 5.
What is the absolute value function?The absolute value function, of vertex (h,k), is defined by the following piecewise rule, depending on the input of the function:
f(x) = |x - h| + k = x - h + k, x - h ≥ 0.f(x) = |x - h| + k = -x + h - k, x - h < 0.In this problem, the coordinates of the vertex are given as follows:
h = 3, as the x-coordinate of the vertex is of 3.k = 5, as the y-coordinate of the vertex is of 5.Hence the vertex is given by the following point:
(3,5).
Then the equation graphed is defined by the rule presented as follows:
y = |x - 3| + 5.
Which is a translation of 3 units right and 5 units up of the standard absolute value function.
More can be learned about the absolute value function at https://brainly.com/question/3381225
#SPJ1
factorization of 120
Answers
Answer:
Step-by-step explanation:
120=10*12
120=5*2*4*3
120=5*2*2*2*3
120=(2^3)*3*5
Prove: The square of the sum of
two consecutive integers is odd.

Answers
\((2n+1)^2=4n^2+4n+1\) therefore, the first blank is 1.
\(4n^2+4n+1=2(2n^2+2n)+1\) therefore, the two other blanks are both 2.
The number in the proof ''The square of the sum of two consecutive integers is odd'' is 2 and 2.
To prove that, The square of the sum of two consecutive integers is odd.
The expression to prove is,
Let us assume that two consecutive integers are n and (n + 1).
Hence, the expression is written as,
[n + (n + 1)]² = (2n + 1)²
= (2n)² + 2 × 2n × 1 + 1²
= 4n² + 4n + 1
= 2 (2n² + 2n) + 1
= odd
Therefore, the number in the blanks are 2 and 2.
To learn more about the Number system visit:
https://brainly.com/question/17200227
#SPJ4
if there were 27600 people in the city Raleigh north Carolina about how much ice cream might they have been expected to consum
Answers
Answer:
27600
Step-by-step explanation:
one for one person
John opened up a new bag of jelly beans and ate three-fourths of the jelly beans in the bag. Then Mike ate two-thirds of the remaining jelly beans. Finally, Fred ate the ten jelly beans that were left. How many jelly beans were in the unopened bag of jelly beans?
Answers
There were 60 jelly beans in the unopened bag of jelly beans.
Let's work through the problem step by step to find the original number of jelly beans in the bag.
John ate three-fourths of the jelly beans.
This means that he consumed 3/4 of the total number of jelly beans, leaving 1/4 of the original amount.
Mike then ate two-thirds of the remaining jelly beans.
Since 1/4 of the original amount was left after John, Mike ate 2/3 of this remaining 1/4.
To find out how much is left, we need to calculate \((\frac{1}{4} )\times (\frac{2}{3} )\).
\((\frac{1}{4} )\times(\frac{2}{3} )=\frac{2}{12} =\frac{1}{6}\)
Mike ate 1/6 of the original amount, leaving 1/6 of the original amount.
Finally, Fred ate the ten jelly beans that were left.
We know that these ten jelly beans represent 1/6 of the original amount.
Let's calculate how many jelly beans are equal to 1/6.
\(\frac{1}{6} = 10\) jelly beans
Now, we can determine how many jelly beans are equal to 6/6 (the whole).
\(\frac{1}{6} \times6=10\times6=60\) jelly beans
Therefore, there were 60 jelly beans in the unopened bag of jelly beans.
For such more questions on jelly beans
https://brainly.com/question/20750173
#SPJ8
What is the answer to this question?
91
X51
Answers
Answer:
4,641
Step-by-step explanation:
Answer: it would be 4641
Step-by-step explanation:
Because when you multiply 91 and 51 that’s the answer you get
Consider a random variable with population standard deviation 14. given a sample of size 42, you estimate the sample mean to be 31 and construct the 95% confidence interval. afterwards, you are told that the population mean is actually 33. does your confidence interval contain the true mean?
Answers
Yes, the true mean of 33 is within the margin of error of the sample mean, we can conclude that the confidence interval does contain the true mean.
To determine whether the confidence interval contains the true mean of 33, we need to calculate the margin of error for the confidence interval. The margin of error is a measure of the precision of the estimate, and it is calculated using the sample size, the standard deviation of the population, and the desired level of confidence.
For a 95% confidence interval, the margin of error can be calculated using the following formula:
The margin of error = 1.96 * (standard deviation / √sample size)
Plugging in the values, we get:
Margin of error = 1.96 * (14 / √42)
Performing the calculation, we find that the margin of error is 3.39. This means that the sample mean of 31 is likely to be within 3.39 units of the true mean, with a confidence level of 95%.
Since the true mean of 33 is within the margin of error of the sample mean, we can conclude that the confidence interval does contain the true mean. This means that our estimate of the population mean, based on the sample size 42, is likely to be accurate.
To learn more about the mean, visit:
brainly.com/question/23263573
#SPJ4
5.x.10=150 find x
6.x.100=1000
Answers
Answer:
I think X is 3. Sorry if it's wrong!
Step-by-step explanation:
5 x 3 = 15 x 10 = 150
What is the value of x?
x+83°
F
x+14°
X =
G
E
x+83°

Answers
Answer:
午後5時37分ちょうどにあなたの家に来て、あなたが椅子に縛られている間にあなたの両親を殺します.私は武装し、あなたを縛ります。急な動きをしたら、ロケットランチャーかショットガンで頭を吹き飛ばします。あなたの選択!
type that into translate, okay?