square efgh underwent several transformations. a. what is the correct value of dilation d, being it is the value in which this square was transformed or dilated? b. explain how you calculated the value for d.
Answers
The value of dilation (d) cannot be determined without specific measurements or information about the transformation.
To determine the value of dilation (d) for the transformation of square EFHG, we would need more specific information about the transformation. Dilation refers to the process of resizing an object by a certain scale factor while maintaining its shape.
a. Without additional information or given values, it is not possible to determine the specific value of dilation (d) for the square EFHG transformation.
b. To calculate the value for dilation (d), we would typically need the corresponding measurements of the original square and its transformed image. By comparing the corresponding lengths of corresponding sides, we can determine the scale factor.
For example, if the length of a side in the original square EFHG is 4 units and the corresponding side in the transformed square is 8 units, the dilation factor (d) would be 8/4 = 2. This means the transformed square is twice as large as the original square in terms of side length.
Without the specific measurements or any given information about the transformation, it is not possible to calculate the value of dilation (d) for square EFHG.
For more questions on value of dilation
https://brainly.com/question/30292982
#SPJ8
Related Questions
Chef Antonio works at a Latin restaurant and doing a great job. During his yearly evaluation, the owner increased his salary from $42,500 to $46,000. What is the percent of increase, to the nearest whole percent, in Chef Antonio's salary?
Answers
Answer:
8%
Step-by-step explanation:
To find the percent change, we first have to find the amount changed, which is (46000-42500) = 3500. Then, we find what percentage that is of the original amount. Remember that when calculating percentage change, it's important to calculate change with respect to the initial value.
To find the percentage, we can divide 3500 by 42500, and multiply that by 100, resulting in 8 being our nearest whole percent
One of the factors of x^2-25 is (x-5). What is the other factor?
Answers
The other factor of x² - 25 given that one of the factors is; (x - 5) is; (x + 5).
Which expression represents another factor of x² - 25 as required?It follows from the task content that the other factor of x² - 25 is to be determined given that the first factor is ; (x - 5).
Recall from the difference of two squares theorem that;
Given an expression of the form; a² - b²; where a² and b² represent perfect squares:
the expression can be as; (a - b) (a + b).
Hence, since x² and 25 are perfect squares; it follows that the given expression can be written as;
(x - 5) (x + 5)
Ultimately, the other factor is; (x + 5).
Read more on difference of squares;
https://brainly.com/question/24673551
#SPJ1
Ben performed a transformation on trapezoid PQRS to create P′Q′R′S′,
As shown in the figure below:
A four-quadrant coordinate grid is drawn:
Trapezoid PQRS with coordinates at P (-6, -3), Q (-4, -3), R (-2, -5), S (-7, -6) and
Trapezoid P prime Q prime R prime S prime with coordinates at
P prime (3, -6), Q prime (3, -4), R prime (5, -2), S prime (6, -7)
What transformation did Ben perform to create P′Q′R′S′?
a. Rotation of 270° counterclockwise about the origin
b. Reflection across the line of symmetry of the figure
c. Reflection across the Y-axis
d. Rotation of 90° counterclockwise about the origin
Answers
To see this, consider the x-coordinates of the vertices of the original trapezoid PQRS and the transformed trapezoid P′Q′R′S′. The x-coordinates of P and S are negative, while the x-coordinates of Q and R are positive. In the transformed trapezoid, the x-coordinates of P′ and S′ are positive, while the x-coordinates of Q′ and R′ are negative. This suggests that the trapezoid was reflected across the y-axis.
Therefore, the answer is c. Reflection across the Y-axis.
Answer: A - rotation of 270 degrees counterclockwise about the origin
Step-by-step explanation:
When a point is rotated 270 degrees counterclockwise, the points change from (x,y) to (-y,x). We can see this when (-4,-3) turns into (-3,4) which we find by doing (-3,-4(-1).
plz help asap 14 points
Latoya created a factor tree and wrote the prime factorization of 90 shown below.
A factor tree of 90. 90 branches to 9 and 10. 9 branches to 3 and 3. 10 branches to 2 and 5. The equation is 90 = 2 times 3 times 5.
What is Latoya’s error?
She should not have found the factors of 9.
She should have included an exponent of 2 on the 3.
She should have included 9 and 10 in the prime factorization.
She should have started the tree with 2 times 45.
Answers
Answer:
B
Step-by-step explanation:
Latoya created a factor tree and wrote the prime factorization of 90 shown below.
A factor tree of 90. 90 branches to 9 and 10. 9 branches to 3 and 3. 10 branches to 2 and 5. The equation is 90 = 2 times 3 times 5.
What is Latoya’s error?
She should not have found the factors of 9.
She should have included an exponent of 2 on the 3.
She should have included 9 and 10 in the prime factorization.
She should have started the tree with 2 times 45.
Hope this helps!!!!!!
Answer:
B
Step-by-step explanation: make it brainleist plz
What is x=17+3
What does x equals
Ps hi Wana be friends
Answers
Answer:x=20
Step-by-step explanation:You would keep x by itself and you would add 17+3 which would equal 20.So therefore the answer would be x=20.
In which situation below would you want to use the Explicit Formula instead of the Recursive Formula?
a. Find the 100th term when the first term is -3 and the common difference is 4.
b. Find the 3rd term when the first term is 2 and the common difference is 5.
c. Find the 7th term when the first term is -1 and the common difference is 10.
d. Find the 5th term when the first term is 7 and the common difference is -2.
Answers
Answer:
Find the 100th term when the first term is -3 and the common difference is 4.
Step-by-step explanation:
Answer:
a
Step-by-step explanation:
Find the 100th term when the first term is -3 and the common difference is 4. I took the test and got 100 percent.
Find k such that the function is a probability density function
over the given interval. Then write the probability density
function. f(x)=ke^x [3,7]
Answers
The probability density function is:
f(x) = (1 / (e⁷- e³)) × eˣ
To determine the value of k that makes the function a probability density function (PDF) over the interval [3, 7], we need to ensure that the integral of the PDF over the entire interval is equal to 1.
The probability density function is given by:
f(x) = keˣ
To find k, we integrate the PDF over the interval [3, 7] and set it equal to 1:
1 = ∫[3,7] keˣ dx
Integrating keˣ with respect to x gives us:
1 = k ∫[3,7] eˣdx
To evaluate this integral, we can use the property that the integral of eˣ is eˣ + C, where C is a constant.
1 = k(e⁷- e³)
Now, we can solve for k:
k = 1 / (e⁷ - e³)
Therefore, the value of k that makes the function a probability density function over the interval [3, 7] is k = 1 / (e⁷ - e³).
The probability density function is:
f(x) = (1 / (e⁷- e³)) × eˣ
Learn more about probability density function here:
https://brainly.com/question/31039386
#SPJ11
14=s/3 what does s equal
Answers
14x 3= 42
S= 42
===============================================
Explanation:
To isolate s, we need to undo the division. We'll multiply both sides by 3
14 = s/3
3*14 = 3*(s/3)
42 = s
s = 42
-------
As a check,
14 = s/3
14 = 42/3 .... replace s with 42
14 = 14
We get the same thing on both sides, so this confirms we have the correct value of s.
PLEASE SOMEONE PLEASE HELP ME WHAT DOES T=

Answers
Answer:
9/4 or 2.25
Step-by-step explanation:
9=4t
Move the 4
9/4=t in decimal its 2.25=t
Can you guys help me with this too? Thank you :)))

Answers
Answer:
x = 10
Step-by-step explanation:
First look at the big overall triangle.
It has a right angle and another angle of 44; therefore the missing angle is (since the sum of angles inside a triangle is 180)
180 - 90 - 44 = missing angle
missing angle (top) = 46; now the angle of a straight line is 180 and they give you 56° which has a supplementary angle of 180 - 56 = 124°.
Now we know that the triangle that include the x has angles 46° (missing top angle), and supplementary angle of 124°. Therefore
x = 180 - 46 - 124
x = 10
Consider a circle whose equation is x2 + y2 – 2x – 8 = 0. Which statements are true? Select three options.
The radius of the circle is 3 units.
The center of the circle lies on the x-axis.
The center of the circle lies on the y-axis. The standard form of the equation is (x – 1)² + y² = 3.
The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9.
Answers
The three (3) statements which are true include the following:
A. The radius of the circle is 3 units.
B. The center of the circle lies on the x-axis.
D. The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9.
What is the equation of a circle?Mathematically, the standard form of the equation of a circle is represented by this mathematical expression;
(x - h)² + (y - k)² = r² ....equation 1.
Where:
h and k represents the coordinates at the center of a circle.
r represents the radius of a circle.
From the information provided, we have the following equation of a circle:
x² + y² – 2x – 8 = 0 ......equation 2.
In order to determine the true statements, we would rewrite the equation in standard form and then factorize by using completing the square method:
x² – 2x + y² = 8 = 0
x² – 2x + (2/2)² + y² = 8 + (2/2)²
x² – 2x + 1 + y² = 8 + 1
(x – 1)² + (y - 0)² = 9 .......equation 3.
Comparing equation 1 and equation 3, we have the following:
Center (h, k) = (1, 0)
Radius, r = 3
Additionally, this line and the circle's center lies on the x-axis because the y-value is equal to zero (0).
(x – 0)² + (y - 0)² = 3²
x² + y² = 9.
Read more on equation of a circle here: brainly.com/question/17028215
#SPJ1
i need help on My homework help me

Answers
Answer:
x = 18
Step-by-step explanation:
1/2 x - 7 = 1/3 (x - 12) Remove the brackets on the right
1/2x - 7 = 1/3 x - 12*1/3
1/2x - 7 = 1/3 x - 4 Subtract 1/3 x from both sides
1/2x - 1/3x - 7 = - 4 Combine like terms on the left
1/6x - 7 = - 4 Add 7 to both sides
1/6 x = - 4 + 7 Combine the right side
1/6 x = 3 Multiply both sides by 6
6 * 1/6x = 3*6
x = 18
find the common difference of the arithmetic sequence 15,22,29, …

Answers
Answer:
7
Step-by-step explanation:
You want the common difference of the arithmetic sequence that starts ...
15, 22, 29, ...
Difference
The common difference is the difference between a term and the one before. It is "common" because the difference is the same for all successive term pairs.
22 -15 = 7
29 -22 = 7
The common difference is 7.
<95141404393>
Dolores spent $13.00 of the $20.00 in her wallet. Which decimal fraction represents the fraction of the $20.00 Dolores spent?
Answers
Answer: 65
Step-by-step explanation:
Use the given values of n and p to find the minimum usual value - 20 and the maximum usual value y + 20. Round to the nearest hundredth unless otherwise noted. n = 100; p = 0.26 O A. Minimum: 21.61; maximum: 30.39 OB. Minimum: 17.23; maximum: 34.77 OC. Minimum: -12.48; maximum: 64.48 OD. Minimum: 34.77; maximum: 17.23
Answers
The answer is OC. Minimum: -12.48; maximum: 64.48.
The minimum usual value - 20 and the maximum usual value y + 20 for the given values of n and p, n = 100; p = 0.26 are found below.
Minimum usual value = np - z * sqrt(np(1 - p)) = 100 × 0.26 - 1.645 × sqrt(100 × 0.26 × (1 - 0.26))= 26 - 1.645 × sqrt(100 × 0.26 × 0.74) = 26 - 1.645 × sqrt(19.1808) = 26 - 1.645 × 4.3810 = 26 - 7.2101 = 18.79 ≈ 18.80
Maximum usual value = np + z * sqrt(np(1 - p)) = 100 × 0.26 + 1.645 × sqrt(100 × 0.26 × (1 - 0.26))= 26 + 1.645 × sqrt(100 × 0.26 × 0.74) = 26 + 1.645 × sqrt(19.1808) = 26 + 7.2101 = 33.21 ≈ 33.22
Therefore, the minimum usual value - 20 is 18.80 - 20 = -1.20.The maximum usual value y + 20 is 33.22 + 20 = 53.22.
Hence, the answer is OC. Minimum: -12.48; maximum: 64.48.
To know more about Minimum visit:
brainly.com/question/27806465
#SPJ11
The circle graph shows how a family spends its annual Income. If $25,200 is used for Food, Savings, and Insurance combined, what is the total annual income?
housing 21%
food 18%
clothing 17%
auto 14%
entertaining 12%
insurance 11%
savings 7%
Answers
Answer:41,328
Step-by-step explanation:
18+7+11=36 36%
100-36=64 64%
25,200 x 164%=41,328
At a temple to Sekhmet, there is a circular reed bed to be planted with 4 different types of reed, one in each of the four sections, as shown here. The radius is 360cm and there are two strings crossing at right angles of lengths 560cm and 640cm.
Find out how far from the centre of the circle the crossing point is.
Answers
Answer:
Step-by-step explanation:
4:6 it is wrng
Answer: 280.28cm
See attached ppt file
Company A is financed by 26% of debt and the rest of the company is financed by common equity. The company's before-tax cost of debt is 3.2%. Currently the risk-free rate is 1.1%, the market risk premium is 6%, and the stock has a beta of 0.9. If company A faces a marginal tax rate of 30%, its weighted average cost of capital (WACC) should be ___ (Note: Round your answer as decimals with three decimal places. For example, if your answer is 8.7%, you should write 0.087 in the answer box. DO NOT write your answer as percentages as you will be marked wrong.)
Answers
The WACC for Company A is approximately 0.564 or 56.4%.
To calculate the weighted average cost of capital (WACC) for Company A, we need to consider the cost of debt and the cost of equity, weighted by their respective proportions in the company's capital structure.
Given information:
Debt proportion (D/V) = 26%
Equity proportion (E/V) = 100% - 26% = 74%
Before-tax cost of debt (r_d) = 3.2%
Risk-free rate (r_f) = 1.1%
Market risk premium (RPM) = 6%
Beta (β) = 0.9
Marginal tax rate (T) = 30%
The formula to calculate WACC is as follows:
WACC = (D/V) * r_d * (1 - T) + (E/V) * r_e
To calculate the cost of equity (r_e), we can use the Capital Asset Pricing Model (CAPM):
r_e = r_f + β * RPM
Plugging in the given values:
r_e = 1.1% + 0.9 * 6% = 1.1% + 5.4% = 6.5%
Now, let's calculate WACC:
WACC = (0.26) * 3.2% * (1 - 0.30) + (0.74) * 6.5%
WACC = 0.0832 + 0.481
WACC ≈ 0.5642
Rounding to three decimal places, the WACC for Company A is approximately 0.564 or 56.4%.
Please note that the WACC represents the average rate of return required by both debt and equity investors to finance the company.
To know more about WACC:
https://brainly.com/question/30746642
#SPJ11
pls help me with my homework

Answers
When there is a negative in front of the exponent it makes a fraction. It is usually just 1/the number it equals if it were positive.
Answer:
\( \frac{1}{81} \)
Step-by-step explanation:
express that with a positive exponent using this:
\( {a}^{ - n} \frac{1}{ {a}^{n} } \)
so ..
\( {9}^{ - 2} = \frac{1}{ {9}^{2} } \)
now you have to evaluate the exponent/ power
so..
\( \frac{1}{ {9}^{2} } = \frac{1}{81} \)
why 81 ?
because the exponent of 9 is 2 so you have to multiple 9 by itself so
9x9=81
so the answer is
\( \frac{1}{ {81}^{} } \)
sorry for the bad english hehe
The variable data refers to the list [10, 20, 30]. After the statement data[1] = 5, data evaluates to
[10, 5, 30]
[5, 10, 20]
[10, 5, 20]
[5, 20, 30]
Answers
The variable data refers to the list [10, 20, 30]. After the statement data[1] = 5, data evaluates to [10, 5, 30]. A list is one of the compound data types that Python provides. Lists can contain items of different types, but they are usually all the same type.
Lists are mutable sequences, meaning that their elements can be changed after they have been created. Lists can be defined in several ways, including by enclosing a comma-separated sequence of values in square brackets ([ ]).
The elements of a list can be accessed using indexing, with the first element having an index of 0. The second element has an index of 1, the third element has an index of 2, and so on. To change the value of an element in a list, you can use indexing with an assignment statement.
For example, the statement `data[1] = 5` changes the second element of the `data` list to 5. Therefore, after this statement, the `data` list will be `[10, 5, 30]`.
To learn more about Python visit;
https://brainly.com/question/30391554
#SPJ11
Give a function that does not have an inflection point at a point where f"(x) = 0.
Answers
f"(x) = 0 at x = 0, but f(x) does not have an inflection point at x = 0 because the second derivative does not change sign at that point. In fact, f(x) is a convex function for all values of x, meaning it curves upwards and has no inflection points.
An inflection point is a point on a curve where the concavity changes, meaning that the second derivative of the function changes sign. Specifically, if f(x) is a twice-differentiable function, then a point c is an inflection point if f''(c) = 0 and the sign of f''(x) changes when x passes through c.
However, it is possible for a function to not have an inflection point at a point where f''(x) = 0. This can occur when the sign of f''(x) does not change as x passes through the point, meaning that the concavity does not change.
One simple example of such a function is f(x) = x^4. This function has a second derivative of f''(x) = 12x^2, which equals zero at x = 0. However, the sign of f''(x) is always positive, meaning that the concavity is always upward and does not change at x = 0. Therefore, f(x) does not have an inflection point at x = 0 despite f''(0) = 0.
In general, any even-degree polynomial will have a second derivative that equals zero at the origin, but the concavity will not change at the origin if the leading coefficient is positive. Other examples of functions that do not have inflection points at points where f''(x) = 0 include functions with constant concavity, such as f(x) = x^2 or f(x) = sin(x).
To learn more about inflection point visit:https://brainly.com/question/30760634
#SPJ11
Write 2x10^2 + 3x10^-3 as a decimal.
Answers
Answer:= 3.456 × 1011
Step-by-step explanation:
which equation represents a line that is parallel to y = 4x + 3 and passes through the point (-3, 2)
50 points
Answers
Answer:
it should be y= -4x + 10
Step-by-step explanation:
hope this helps.
What is the mean of the data set?
{7, 9, 5, 4, 3, 6, 8}
Enter your answer in the box.
Answers
Explanation: to find the mean (average) of a data set you add up all of the numbers and then divide by how many are present.
7+9+5+4+3+6+8=42
Since there are 7 numbers present we divide our answer by 7.
42/7 = 6
So the mean of the data set is 6
If you spend $50,000 on new furniture and it is depreciating about 20% per year, how much will it be worth by its third year?
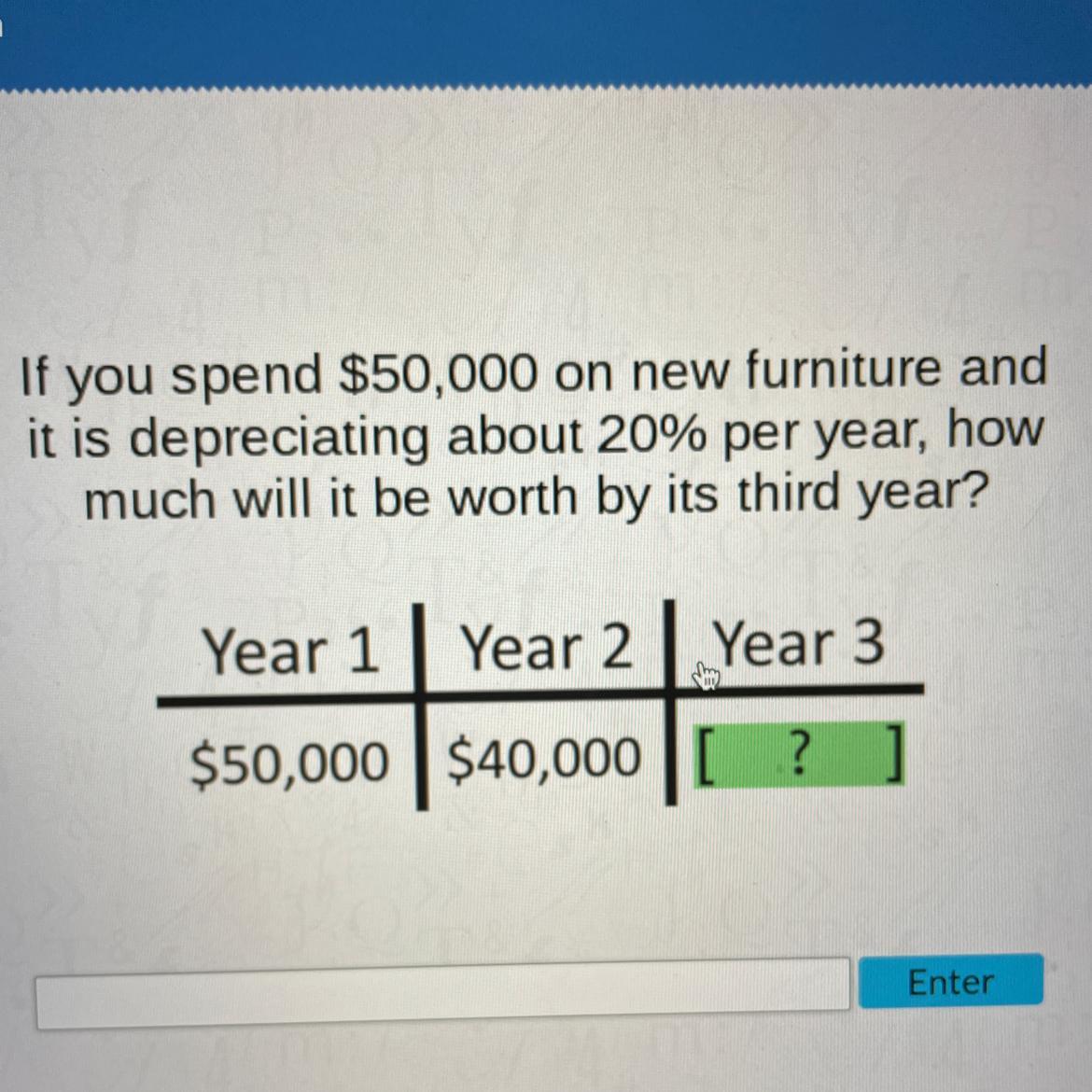
Answers
Answer:
$25,600
Step-by-step explanation:
Given: P = $50,000, r = 20% & t = 3 yearsFormula for depreciation is given as:\(A(t) = P\bigg(1-\frac{r}{100}\bigg)^t\)Plugging the values of P, r and t in the above formula, we find:\(A(3) = 50,000\bigg(1-\frac{20}{100}\bigg)^3\)\(\implies A(3) = 50,000\bigg(1-\frac{1}{5}\bigg)^3\)\(\implies A(3) = 50,000\bigg(\frac{4}{5}\bigg)^3\)\(\implies A(3) = 50,000\times\frac{64}{125}\)\(\implies A(3) =\$ 25,600\)So, after third year it will be worth by $25,600.what is the last digit of 3 with a power of 2011
Answers
So to find any last digit of 3^2011 divide 2011 by 4 which comes to have 3 as remainder. Hence the number in units place is same as digit in units place of number 3^3. Hence answer is 7.
can someone answer page 3 question 3, page 5 question 3, all of page 6
Answers
The answers to the questions involving trigonometry are: 90, BC/AB ÷ BC/AB = 1, g = 6.5, <I = 62 degrees, h= 13.8, 12.0, x = 6.8, x = 66.4, 160.6, The pole = 6.7
What is trigonometrical ratios?Trigonometric ratios are special measurements of a right triangle, defined as the ratios of the sides of a right-angled triangle. There are three common trigonometric ratios: sine, cosine, and tangent
For page 3 question 3,
a) <A + <B = 90 since <C = right angle
b) SinA = BC/AB and CosB = BC/AB
The ratio of the two angles BC/AB ÷ BC/AB = 1
I notice that the ratio of sinA and cosB gives 1
b) The ratio of CosA and SinB will give
BC/AB ÷ BC/AB
= BC/AB * AB/BC = 1
For page 5 number 3
Tan28 = g/i
g/12.2 = tan28
cross multiplying to have
g = 12.2*tan28
g = 12.2 * 0.5317
g = 6.5
b) the angle I is given as 90-28 degrees
<I = 62 degrees
To find the side h we use the Pythagoras theorem
h² = (12.2)² + (6.5)²
h² = 148.84 +42.25
h²= 191.09
h=√191.09
h= 13.8
For page 6
1) Sin42 = x/18
x=18*sin42
x = 18*0.6691
x = 12.0
2) cos28 = 6/x
xcos28 = 6
x = 6/cos28
x [= 6/0.8829
x = 6.8
3) Tan63 = x/34
x = 34*tan63
x= 34*1.9526
x = 66.4
4) Sin50 123/x
xsin50 = 123
x = 123/sin50
x = 123/0.7660
x =160.6
5) Sin57 = P/8
Pole = 8sin57
the pole = 8*0.8387
The pole = 6.7
Learn more about trigonometrical ratios on https://brainly.com/question/23130410
#SPJ1
Solve the following initial value problem y ′′ + y ′ + 4.25y = cos(x), y(0) = 0, y ′ (0) = 1
Solve the following initial value problem y ′′ + 5y ′ + 4y = 3e^(2t) , y(0) = 1, y ′ (0) = 0
Find the general solution of y ′′ − y = x − e^(−x)
Find the general solution of y ′′ − 3y ′ − 4y = 4t
Answers
1)General solution is : y(x) = c1 cos(1.5x) + c2 sin(1.5x) - (1/17) cos(x) + (4/17) sin(x)
2)general solution of the given differential equation is:y(x) = c1 e^(4x) + c2 e^(-x) + t
1) The general solution of the given initial value problem can be found by solving the characteristic equation r2 + r + 4.25 = 0.
The roots of the equation are:r1,2 = (-1 ± √(1 - 4·4.25)) / (2) = (-1 ± 1.5i)
The general solution is given by:'
y(x) = c1 cos(1.5x) + c2 sin(1.5x) + y_p where y_p is the particular solution.
To find y_p, we can use the method of undetermined coefficients.
Let's assume that y_p = A cos(x) + B sin(x).y′′ + y′ + 4.25y = cos(x)y′
= - A sin(x) + B cos(x)y′′
= - A cos(x) - B sin(x)y′′ + y′ + 4.25y
= (-A + B + 4.25A cos(x) + 4.25B sin(x)) cos(x) + (-B - A + 4.25A sin(x) - 4.25B cos(x)) sin(x)
Comparing the coefficients of cos(x) and sin(x), we get:-A + B + 4.25A = 0-B - A - 4.25B = 1
Solving for A and B, we get: A = -1/17, B = 4/17
Therefore, the particular solution is:
y_p = (-1/17) cos(x) + (4/17) sin(x)
Finally, the general solution of the given initial value problem is:
y(x) = c1 cos(1.5x) + c2 sin(1.5x) - (1/17) cos(x) + (4/17) sin(x)
2) The given initial value problem can be solved by finding the roots of the characteristic equation r2 + 5r + 4 = 0.
The roots are:r1,2 = (-5 ± √(25 - 4·4)) / (2) = -1, -4
The general solution is given by:
y(x) = c1 e^(-x) + c2 e^(-4x) + y_p where y_p is the particular solution.
To find y_p, we can use the method of undetermined coefficients.
Let's assume that y_p = A e^(2t).y′′ + 5y′ + 4y = 3e^(2t)y′ = 2A e^(2t)y′′
= 4A e^(2t)y′′ + 5y′ + 4y
= (4A + 10A + 4A e^(2t)) e^(2t)
Comparing the coefficients of e^(2t), we get:4A + 10A = 3
Solving for A, we get: A = 3/14
Therefore, the particular solution is:y_p = (3/14) e^(2t)
Finally, the general solution of the given initial value problem is:
y(x) = c1 e^(-x) + c2 e^(-4x) + (3/14) e^(2t)3)
The characteristic equation of the given differential equation is r2 - 1 = 0.
The roots of the equation are:r1,2 = ±1
The general solution is given by:
y(x) = c1 e^(x) + c2 e^(-x) + y_pwhere y_p is the particular solution.
To find y_p, we can use the method of undetermined coefficients.
Let's assume that y_p = Ax + Be^(-x).y′′ − y
= x − e^(−x)y′ = A - Be^(-x)y′′
= - Be^(-x)y′′ − y
= (- Ax + B + e^(−x))(e^(-x))
Comparing the coefficients of x and e^(-x), we get:
-A + B = 0-1 - B = -1
Solving for A and B, we get: A = -1, B = -1
Therefore, the particular solution is:y_p = -x - e^(-x)
Finally, the general solution of the given differential equation is:y(x) = c1 e^(x) + c2 e^(-x) - x - e^(-x)4)
The characteristic equation of the given differential equation is r2 - 3r - 4 = 0.
The roots of the equation are:r1,2 = (-(-3) ± √((-3)2 - 4·1·(-4))) / (2·1) = 4, -1
The general solution is given by:y(x) = c1 e^(4x) + c2 e^(-x) + y_pwhere y_p is the particular solution.
To find y_p, we can use the method of undetermined coefficients.
Let's assume that y_p = At + B.y′′ − 3y′ − 4y = 4ty′ = Ay′′ = A4y′′ − 3y′ − 4y = 4t(A4 - 3A) + B(4) = 4t
Comparing the coefficients of t, we get: A = 1
Solving for B, we get: B = 0
Therefore, the particular solution is:y_p = t
Finally, the general solution of the given differential equation is:y(x) = c1 e^(4x) + c2 e^(-x) + t
Learn more about differential equation:
brainly.com/question/18760518
#SPJ11
A rectangle is drawn in the first quadrant so that the base lies on the x -axis, bottom left corner on the origin, top right comer is on the line 2y+4x=40. Draw a diagram. Find the maximum area of such a rectangle. 11. A rectangle is drawn in the first and second quadrants so that the base lies on the x -axis, upper left comer on the line y=2x+6, top right corner is on the line y=−2x+6. Draw a diagram. Find the maximum area of such a rectangle.
Answers
a) The maximum area of such a rectangle is 50 square units. b) The maximum area of such a rectangle is 36.
What is Quadratic and Linear equation ?When graphed, a linear equation results in a straight line. Since each value of x results in just one value of y, this relationship is referred to as being one-to-one. When a quadratic equation is graphed, the result is a parabola that extends uphill or downward in the y direction, starting at a single point known as the vertex. Because there are two values for x for every value of y (aside from the y-value at the vertex point), the relationship between x and y is not one-to-one.
a) The given equation is 2y + 4x =40
Let the coordinates of the top right corner be (x,y).
Then, y = (40 -4x)/2
The area of the rectangle is given by A =xy
A= x x (40 -4x)/2
A = 20x-2x²
We have to find the maximum area of the rectangle.
Differentiate the expression for Area A with respect to x to get the slope of the curve
A’ = 20-4x
At the maximum area, A’=0
Therefore, 20 -4x =0
4x =20
X=5
Substituting x=5 in the equation of the line 2y + 4x =40
2y +20 =40
2y = 20
Y =20
Therefore, the coordinates of the top right corner of the rectangle are (5,10).
The maximum area of the rectangle is given by A = xy = 5 x 10 =50 sq.units
b) The maximum area of such a rectangle can be found by using the formula: A = lw,
where l is the length of the rectangle
w is the width of the rectangle
Since the base of the rectangle is on the x-axis and the upper left corner is on the line y=2x+6, the length of the rectangle is equal to the distance between y=2x+6 and the x-axis, which is 6. The width of the rectangle is equal to the distance between y=-2x+6 and the x-axis, which is also 6. Thus, the maximum area of such a rectangle is 36 square units.
To know more about linear and quadratic equation visit: https://brainly.com/question/12788590
#SPJ4
Please help!
Provide an appropriate response and show your work. Assume that the random variable X is normally distributed, with mean=90 and standard deviation=12. Compute the probability P(57 < X < 105).
Answers
The probability that X is between 57 and 105 is 0.8914.
How to solveGiven:
* X is normally distributed with mean=90 and standard deviation=12
* P(57 < X < 105)
Solution:
* Convert the given values to z-scores:
* z = (X - μ) / σ
* z = (57 - 90) / 12 = -2.50
* z = (105 - 90) / 12 = 1.25
* Use the z-table to find the probability:
* P(Z < -2.50) = 0.0062
* P(Z < 1.25) = 0.8944
* Add the probabilities to find the total probability:
* P(57 < X < 105) = 0.0062 + 0.8944 = 0.8914
Therefore, the probability that X is between 57 and 105 is 0.8914.
Read more about probability here:
https://brainly.com/question/24756209
#SPJ1