Answers
For everyone 1 it goes up it moves over 12
Related Questions
find the area of the surface. the part of the plane 5x + 2y + z = 10 that lies in the first octant
Answers
Answer:
5√30 ≈ 27.386 square units
Step-by-step explanation:
You want the area of the portion of the plane 5x +2y +z = 10 that lies in the first octant.
InterceptsThe axis-intercepts are found by setting the other variables to zero.
x-intercept: 5x = 10 ⇒ x = 2
y-intercept: 2y = 10 ⇒ y = 5
z-intercept: z = 10
Side LengthsThe boundaries of the triangular first-octant portion of the plane will be the lines between these intercepts. The length of each boundary can be found using the distance formula. For example, the length in the X-Y plane will be ...
d = √((x2 -x1)² +(y2 -y1)² +(z2 -z1)²)
d = √((0 -2)² +(5 -0)² +(0 -0)²) = √(4+25) = √29
The first attachment shows the other side lengths to be ...
Y-Z plane: 5√5
X-Z plane: 2√26
AreaThe area of the triangular portion of the plane can be found using Heron's formula. For semi-perimeter s and side lengths a, b, c, the area is ...
A = √(s(s -a)(s -b)(s -c)) . . . . . . where s = (a+b+c)/2
The second attachment shows the area to be 5√30 ≈ 27.386 square units.
#95141404393


The approximate value of the surface area is 4.32 square units.
To find the area of the surface, we need to first find the equation of the plane and then determine the portion of the plane that lies in the first octant.
The equation of the plane can be written as:
z = 10 - 5x - 2y
To determine the portion of the plane that lies in the first octant, we need to find the points where the plane intersects the x, y, and z axes. Setting x = 0, y = 0, and z = 0 in the equation of the plane, we get:
z = 10 (when x = 0 and y = 0)
y = 5x (when z = 0 and y = 0)
x = 2 (when z = 0 and x = 0)
The portion of the plane that lies in the first octant is bounded by the x-axis, the y-axis, and the line y = 5x. To find the area of this surface, we can use a double integral:
∬R √(1+f_x^2+f_y^2) dA
where R is the region bounded by the x-axis, the y-axis, and the line y = 5x, and f(x,y) = 10 - 5x - 2y.
Converting to polar coordinates, we have:
x = r cosθ
y = r sinθ
The line y = 5x becomes y = 5r cosθ, and the region R is described by:
0 ≤ r ≤ 2sinθ
0 ≤ θ ≤ π/4
The surface area is then:
A = ∫(0 to π/4) ∫(0 to 2sinθ) √(1+f_r^2+f_θ^2) r dr dθ
Using f(x,y) = 10 - 5x - 2y, we can find:
f_r = -5
f_θ = -2r
So we have:
A = ∫(0 to π/4) ∫(0 to 2sinθ) √(1+25+4r^2) r dr dθ
= ∫(0 to π/4) ∫(0 to 2sinθ) √(29+4r^2) r dr dθ
This integral is difficult to evaluate analytically, but it can be approximated using numerical methods or a computer algebra system.
To know more about surface area,
https://brainly.com/question/31383036
#SPJ11
Question 6(Multiple Choice Worth 2 points)
(Linear Relationships MC)
At a restaurant, hot chocolate can be purchased in three different cup sizes. A 12-ounce cup costs $1.97, a 16-ounce cup costs $2.62, and a 20-ounce cup costs $3.27.
Which statement is true based on the given description?
O The description shows a linear relationship, but not a proportional relationship.
O The description shows a linear relationship and a proportional relationship.
O The description does not show a linear relationship or a proportional relationship.
O The description shows a proportional relationship, but not a linear relationship
Answers
We need to know about linear and proportional relationship to solve this problem. Statement 2 is true, the description shows a linear relationship and a proportional relationship.
Linear relationship is a relationship between two variables where if one increases the other increases or if one decreases the other decreases. The varibales in a linear relationship form a straight line on graph. Proportional relationship is the relationship between two variables where the ratio between pairs of different data always remains constant. In the given question, a 12 ounce cup costs $1.97, a 16 ounce cup costs $2.62 and a 20 ounce cup costs $3.27. The price of each cup increases with increase in capacity of the cup, so we can say that the cup capacity and price have a linear relationship. The ratio between each pair can be given by
12/1.97=6.10
16/2.62=6.10
20/3.27=6.10
The ratios between every pair is same, so it is a proportional relationship.
Thus we found that the description shows a linear relationship and a proportional relationship between the cup capacity and it's price, statement 2 is the right option.
Learn more about proportional relationship here:
https://brainly.com/question/13550871
#SPJ9
Expand and simplify (x - 3)(x + 5)
Answers
Answer:X\(x^{2} +2x-15\)
Step-by-step explanation: you do it by multiplying out the brackets and then you simplify the result expression by collecting the like terms.
12 less than a number is equal to the product of 7 and that number. Convert into an
equation and find the number?
Answers
Answer:
EQUATION: X - 12 = 7X. SOLUTION: X = - 2.
Step-by-step explanation:
First, we do not know the number. When the number is unknown, it is a variable. I chose the variable, "X."
12 less than signals that we subtract 12. So that would be X - 12.
A product of 7 AND that number means we multiply 7 by X. That can be notated as 7X.
12 less than X is EQUAL to the product of 7 and X. So X - 12 = 7X.
To find the solution, we want to know the value of X. Move X to one side of the equation.
X - 12 = 7X
-X -X
_________
-12 = 6X
Divide both sides by 6 to get X by itself.
X = - 2.
Need help ASAP thanks only answer if you know please don’t answer just for points I need help

Answers
Answer- 30
Step-by-step explanation:
Set up the limit of integration of the volume of the solid
bounded from above by , and from below by and inside
the cone in cylindrical coordinates. (Do
not evaluate)
Answers
The set up the limit of integration of the volume of the solid bounded from above by 3+z=9 or z=6 and from below by 2+z=4 or z=2 and inside the cone in cylindrical coordinates is given below:
V = ∫(0 to 2π) ∫(2 to 6) ∫(0 to (z-2)tan θ) r dr dz dθ
The solid is bounded from above by 3+z=9 or z=6.
The solid is bounded from below by 2+z=4 or z=2.
The cone is a circular cone having vertex at the origin and a radius of 4.
In order to set up the limit of integration of the volume of the solid bounded from above by 3+z=9 or z=6 and from below by 2+z=4 or z=2 and inside the cone in cylindrical coordinates, we need to draw a diagram for the given situation.
After drawing the diagram, we get the following figure:
figure { width: 350px; height: 350px; }
By observing the above figure, we can say that the cone is symmetric about the z-axis.
So, we can take the limits of r from 0 to the radius of the cone at the corresponding height of z. The radius of the cone at a corresponding height of z is given by:
r= h (tan θ)
Where θ is the half angle of the cone which is given by tan θ = 4/8 = 0.5θ = 26.57°
By substituting h = z-2 in the above equation, we get:
r = (z-2)tan θ
The limits of z are given from 2 to 6.
Volume of the given solid in cylindrical coordinates is given by:
V = ∫(0 to 2π) ∫(2 to 6) ∫(0 to (z-2)tan θ) r dr dz dθ
So, the set up the limit of integration of the volume of the solid bounded from above by 3+z=9 or z=6 and from below by 2+z=4 or z=2 and inside the cone in cylindrical coordinates is given below:
V = ∫(0 to 2π) ∫(2 to 6) ∫(0 to (z-2)tan θ) r dr dz dθ
Learn more about volume
brainly.com/question/28058531
#SPJ11
Some information is given about each sphere. Order them from least volume to greatest volume. You may sketch a sphere to help you visualize if you prefer.
Sphere A: Has a radius of 4
Sphere B: Has a diameter of 6
Sphere C: Has a volume of 64
Sphere D: Has a radius double that of sphere B.
Answers
The least volume to greatest volume will be sphere B, sphere C, sphere A and sphere D.
What will be the volume of the sphere?The volume of the sphere is calculated as:
= 4/3 πr³
where r = radius
The volume of sphere A will be:
= 4/3 πr³
= 4/3 × π × 4³
= 85.3π
The volume for sphere B will be:
= 4/3 πr³
= 4/3 × π × (6/2)³
= 4/3 × π × 3³
= 36π
The volume for C is given as 64π.
The volume for D has a radius double that of B. This will be Radius = 3 × 2 = 6
= 4/3 πr³
= 4/3 × π × 6³
= 288π
Learn more about volume on:
brainly.com/question/1972490
#SPJ1
A rectangle has a length of 5x+2 and a width of 3x - 1. If x=10, what is the perimeter and area?
Answers
Answer:
Perimeter = 162 units
Area = 1508 square units
Step-by-step explanation:
Given expressions:
Length = 5x + 2Width = 3x - 1If x = 10, then:
Length = 5(10) + 2 = 52Width = 3(10) - 1 = 29The formula for the perimeter of a rectangle is:
P = 2(w + l)where w is the width and l is the length.
Therefore, the perimeter of the rectangle is:
\(\implies \sf P = 2(29 + 52)\)
\(\implies \sf P = 2(81)\)
\(\implies \sf P = 162\;units\)
The formula for the area of a rectangle is:
A = w · lwhere w is the width and l is the length.
Therefore, the area of the rectangle is:
\(\implies \sf A=29 \cdot 52\)
\(\implies \sf A=1508\;square\;units\)
Answer:
Area of rectangle = 1508
Perimeter of rectangle = 162
Step-by-step explanation:
Now we have to,
→ find the perimeter and area.
→ where x = 10.
Perimeter of rectangle is,
→ P = 2 × (L + W)
→ P = 2 × (5(10) + 2 + 3(10) - 1)
→ P = 2 × (50 + 2 + 30 - 1)
→ P = 2 × 81
→ [ P = 162 ]
Area of rectangle will be,
→ A = L × W
→ A = (5(10) + 2) × (3(10) - 1)
→ A = (50 + 2) × (30 - 1)
→ A = 52 × 29
→ [ A = 1508 ]
Hence, these are the values.
why do the last ten or so data points have a relatively higher percent error? Consider the Ricardian trade model with zero tariffs and transportation costs between two countries (a) Are the output prices equalized between the two trading countries?
Answers
According to the Ricardian model, the difference in technology among nations causes output per worker in each country to differ.
The model is limited in several ways: 1. Having only 1 factor of production is way too simplistic a view of manufacturing. 2. In real world, almost no country produces only the goods in which they have a comparative advantage.
The Ricardian model assumes that labour is the only factor of production. Under this assumption, the only possible source of comparative advantage is differences between countries in labour productivity.
An important criticism leveled against Ricardian theory of rent concerns the relation between rent and price. According to Ricardo, price determines rent. The higher the price of corn, the higher will be the rent. The price of corn is determined by the cost of producing corn on the marginal land which is rent-free.
Therefore,
According to the Ricardian model, the difference in technology among nations causes output per worker in each country to differ.
To learn more about Ricardian trade visit :
brainly.com/question/15352601
#SPJ4
Can someone please explain the fetch-decode-execute cycle in computer science
Answers
After answering the presented question, we can conclude that A function computer can execute a sequence of instructions that make up a computer programme by following this cycle.
What is function?In mathematics, a function appears to be a link between two sets of numbers in which each member of the first set (known as the domain) corresponds to a specific member of the second set (called the range). In other words, a function takes input from one collection and creates output from another. The variable x has frequently been used to represent inputs, whereas the variable y has been used to represent outputs. A formula or a graph can be used to represent a function. For example, the formula y = 2x + 1 depicts a functional form in which each value of x generates a unique value of y.
The fetch-decode-execute cycle, also known as the instruction cycle, illustrates how a computer's CPU (Central Processor Unit) gets instructions from memory, decodes them, and then executes them. Here's a quick rundown of each step:
Fetch: Based on the current value of the programme counter (PC) register, which corresponds to the memory address of the next instruction to be executed, the CPU retrieves the next instruction from memory.
The fetch-decode-execute cycle is an essential component of the von Neumann architecture, which serves as the foundation for most modern computers. A computer can execute a sequence of instructions that make up a computer programme by following this cycle.
To know more about CPU visit:
https://brainly.com/question/16254036
#SPJ1
Ms. Perreca examines several math errors of one of her students to try to figure out the pattern of errors. What is the pattern of error for these particular problems?
10+ 6 = 4
11 - 5 = 16
Answers
The pattern of error seems to be adding 4 and subtracting 10 in each calculation.
In the first example, the student adds 4 to the correct sum of 10 and 6, resulting in 14 instead of the correct answer of 16. In the second example, the student subtracts 10 from the correct difference of 11 - 5, resulting in 1 instead of the correct answer of 6.
From these examples, we can observe a consistent pattern in the errors made by the student. Specifically, the student is adding 4 to the correct sum and subtracting 10 from the correct difference. This suggests that the student may have misunderstood or misapplied the rules of addition and subtraction.
Learn more about pattern at https://brainly.com/question/275463
#SPJ11
Prove the function f :R- {1}\rightarrow?R-{1} defined by f(x)=(\frac{x+1}{x-1})^3is bijective.
Answers
The function f(x) = ((x+1)/(x-1))^3 is bijective as it is both injective and surjective, meaning it has a one-to-one correspondence between its domain and codomain.
To prove that f(x) = \(((x+1)/(x-1))^3\)is bijective, we need to show that it is both injective and surjective.
Injectivity: To prove injectivity, we assume that f(x1) = f(x2) and show that it implies x1 = x2. So, let's assume f(x1) = f(x2) and substitute the function values:
\(((x1+1)/(x1-1))^3 = ((x2+1)/(x2-1))^3\)
Taking the cube root of both sides, we get:
(x1+1)/(x1-1) = (x2+1)/(x2-1)
Cross-multiplying and simplifying, we have:
x1 + 1 = x2 + 1
This implies x1 = x2, which shows that the function is injective.
Surjectivity: To prove surjectivity, we need to show that for every y in the codomain, there exists an x in the domain such that f(x) = y. In this case, the codomain is R - {1}.
Let y be an arbitrary element in R - {1}. We can solve the equation f(x) = y for x:
\(((x+1)/(x-1))^3\)= y
Taking the cube root of both sides, we get:
\((x+1)/(x-1) = y^(1/3)\)
Cross-multiplying and simplifying, we have:
\(x + 1 = y^(1/3)(x - 1)\)
Expanding and rearranging terms, we get:
\((x - y^(1/3)x) = y^(1/3) - 1\)
Factoring out x, we have:
\(x(1 - y^(1/3)) = y^(1/3) - 1\)
Dividing both sides by (1 - y^(1/3)), we get:
\(x = (y^(1/3) - 1)/(1 - y^(1/3))\)
This shows that for any y in R - {1}, we can find an x in the domain such that f(x) = y, proving surjectivity.
Learn more about surjectivity here:
https://brainly.com/question/13656067
#SPJ11
help needed pleasepleasdpleae

Answers
Step-by-step explanation:
it is simple. as you can even see in the answer options, this just means that n = 101.
and then we simply calculate. what's the issue ?
a101 = 12 + (101 - 1)×-2 = 12 + 100×-2 = 12 - 200 = -188
you are aware of the priorities of mathematical operations ?
1. brackets
2. exponents
3. multiplications and divisions
4. additions and subtractions
this is what we did here :
first the bracket.
second the multiplication.
third the subtraction.
Which aspect of Earth's orbital relationship to the Sun varies with a periodicity of both 400 Ka and 100 Ka?
Answers
These cycles are known as the eccentricity cycles, and they are one of the factors that contribute to the long-term climate variations on Earth
The aspect of Earth's orbital relationship to the Sun that varies with a periodicity of both 400 Ka and 100 Ka is the eccentricity of Earth's orbit. The eccentricity refers to the shape of Earth's orbit around the Sun, which is not a perfect circle, but an ellipse. The eccentricity of Earth's orbit changes over time due to gravitational interactions with other planets, particularly Jupiter and Saturn. When Earth's orbit is more elliptical, its distance from the Sun varies more throughout the year, leading to variations in climate and the amount of solar radiation received on Earth's surface. The periodicity of 400 Ka corresponds to a cycle of variations in Earth's eccentricity that affects the amount of solar radiation received at different latitudes and the distribution of ice ages. The periodicity of 100 Ka corresponds to a cycle of variations in Earth's eccentricity that affects the intensity of the seasons and the distribution of glacial periods. These cycles are known as the eccentricity cycles, and they are one of the factors that contribute to the long-term climate variations on Earth.
To learn more about distribution visit:
https://brainly.com/question/29062095
#SPJ11
7. The floor area of a passage is 2,4 m². The floor has to be tiled with square tiles of which the length of the sides is 200 mm. How many tiles do you need to cover the floor?
Answers
The number of tiles needed to cover the floor is 60 tiles.
Given Information,
The floor area of the passage = 2.4 m²
Length of a side of square tile = 200mm
Length of the side is in mm which needs to be converted in its standard form which is meters.
Therefore, the length of side = 200/1000 m
= 0.2 m
Area of the square tile = 0.2 x 0.2
= 0.04 m²
Let the number of tiles be x.
∴ Number of tiles = \(\frac{Area of passage}{Area of each tile}\)
x = 2.4/0.04
x = 60
∴ The number of tiles needed to cover the floor is 60 tiles.
Let's check similar questions on Area : https://brainly.com/question/25092270
Find the area of the triangle below. Be sure to include the correct unit in your answer

Answers
Answer:
Step-by-step explanation:
here
base(b) = 13 yd
height (h) = 4 yd
area of triangle
= 1/2 *b*h
= 1/2 * 13 * 4
= 26 yd²
A science class is tracking the progress of plant growth. The class starts the experiment with a plant five centimeters high. The plant grows two centimeters each day. The model for plant growth "y" is given by: y = 2x + 5. What is the meaning of the y-intercept in this equation?
A) the y-intercept is the starting date
B) the y-intercept is two times larger than five
C) the y-intercept is the starting height of the plant
D) the y-intercept is the largest height the plant can grow
Answers
Answer:
A
Step-by-step explanation:
when growth of plant is zero means x=0 then y=2(0)+5 = 5
ind the area of the region bounded by the curves y=-x^{2}+2 x+2 and y=2 x^{2}-4 x+2 .
Answers
The area of the region bounded by the curves y = -x^2 + 2x + 2 and y = 2x^2 - 4x + 2 is -4/27 square units.
To find the area of the region bounded by the curves y = -x^2 + 2x + 2 and y = 2x^2 - 4x + 2, we need to determine the points of intersection of the two curves. The area can then be calculated by finding the definite integral between these intersection points.
First, we set the two equations equal to each other:
-x^2 + 2x + 2 = 2x^2 - 4x + 2
Rearranging the terms, we have:
3x^2 - 6x = 0
Factoring out x, we get:
x(3x - 6) = 0
This equation is satisfied when x = 0 or x = 2/3.
To find the area between the curves, we integrate the difference between the upper curve and the lower curve with respect to x, from x = 0 to x = 2/3:
Area = ∫[0, 2/3] (2x^2 - 4x + 2) - (-x^2 + 2x + 2) dx
Simplifying, we have:
Area = ∫[0, 2/3] (3x^2 - 6x) dx
Integrating, we get:
Area = [x^3 - 3x^2] evaluated from 0 to 2/3
Plugging in the limits of integration, we have:
Area = [(2/3)^3 - 3(2/3)^2] - [0^3 - 3(0^2)]
Simplifying further, we find:
Area = (8/27 - 4/9) - (0 - 0)
Area = 8/27 - 4/9
Area = 8/27 - 12/27
Area = -4/27
Therefore, the area of the region bounded by the curves y = -x^2 + 2x + 2 and y = 2x^2 - 4x + 2 is -4/27 square units.
The negative value here of the area indicates that the lower curve (y = -x^2 + 2x + 2) lies above the upper curve (y = 2x^2 - 4x + 2) within the given interval.
Learn more about intersection points here:
brainly.com/question/26496929
#SPJ11
If Point P lies on segment QR and QP = 15 and PR = 7, what is the measure of QR?
Answers
Answer:
QR = 22
Step-by-step explanation:
Since, Point P lies on segment QR.
Therefore,
QR = QP + PR
QR = 15 + 7
QR = 22
Which of the following statements best explains why this graph represents a relation that is not a
function?
-The y-values between 1 and 2 are each paired with multiple x-values.
-The x-values between 1 and 3 are each paired with multiple y-values.
-The graph does not pass through the origin.
-The graph extends forever to both the left and the right.
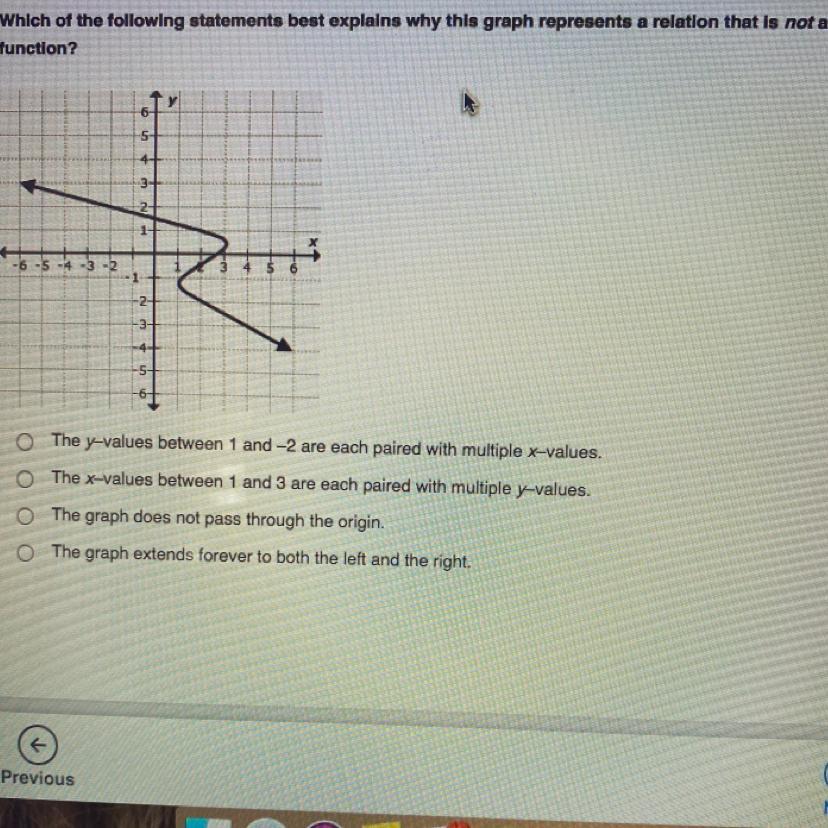
Answers
Answer:
the second answer
Step-by-step explanation: too lazy to explain
Answer:
The 3 the graph extends forever to both the left and the right.
Step-by-step explanation:
PLEASE HELP .. IT NEEDS TOO BE DONE IM STRUGGLING

Answers
Answer:
9+2c
Step-by-step explanation:
9 Josie parents opened a college
savings account that pays yearly
simple interest of 5.5%. They opened
the account with $500 and adds $50
each month to her account. How
much money is in her account at the
end of 4 years?
Record your answer and fill in the
bubbles on your answer document.
Be sure to use the correct place
value.
Answers
Answer:
$1,281.00
Step-by-step explanation:
We start by calculating the value $50 added each month after the first month
= $50 × 11
= $550
Calculation:
First, converting R percent to r a decimal
r = R/100 = 5.5%/100 = 0.055 per year.
P = Principal = 500 + 550
= $1050
Calculation:
First, converting R percent to r a decimal
r = R/100 = 5.5%/100 = 0.055 per year.
Solving our equation:
A = 1050(1 + (0.055 × 4)) = 1281
A = $1,281.00
Therefore, there would be $1,281.00 after 4 years.
helppppp
plsssss!!!!!!

Answers
Answer:
y = 5x – 2
The correct answer is C
solve the following simultaneous equations: 3x+8y = 41
x+2y=11
Answers
Answer:
(3, 4)
Step-by-step explanation:
Using elimination method:
3x + 8y = 41
-3(x + 2y = 11)
-3x -6y = -33
2y = 8
y = 4
x = 3 (plug y back into the equation)
(3, 4)
Answer:
\(3x + 8y = 41 - - (1) \\ x + 2y = 11 - - (2) \\ (2) \: x + 2y = 11 \\ x = 11 - 2y - (3) \\ (3)in(1) is \: \: 3(11 - 2y) - 8y = 41 \\ 33 - 6y + 8y = 41 \\ 33 + 2y = 41 \\ 2y = 41 - 33 \\ 2y = 8 \\ y = \frac{8}{2} \\ y = 4 \\ y = 4 \: in \: (2) \: is \: x + 2(4) = 11 \\ x + 8 = 11 \\ x = 11 - 8 \\ x = 3\)
patients scheduled to see their primary care physician at a particular hospital wait, on average, an additional ten minutes after their appointment is scheduled to start. assume the time that patients wait is exponentially distributed. what is the probability a randomly selected patient will see the doctor within fourteen minutes of the scheduled time?
Answers
Therefore , the solution of the given problem of probability comes out to be 59.3% chance that an arbitrarily chosen patient will see the doctor within 14 minutes of the appointment time.
What precisely is probability?The determination of the likelihood that an assertion is accurate or that a particular event will occur is the main objective of the systems within the process known as criteria. Chance can be represented by any number between 0 and 1, where 0 is frequently used to indicate that it's possible and 1 is frequently used to signify a degree of confidence. A probability diagram shows the likelihood that a particular occurrence will occur.
Here,
With a mean of 10 minutes and an exponential distribution, X has the following probability density function:
=> For x >= 0, f(x) = (1/10) * e(-x/10).
The likelihood that an arbitrarily chosen patient will see the doctor within 14 minutes of the appointment time is what we are trying to determine. This can be stated as follows:
=> P(X <= 14)
Integrate the density function from 0 to 14 to discover this probability:
=> P(X = 14) = e(-x/10) * [0,14] (1/10)
=> P(X = 14) = 0 1.4 e (-u) du
The integral's evaluation yields:
=> P(X <= 14) = [\(-e^{-u}\)] between 0 and 1.4
=> P(X <= 14) = -e⁻¹⁴ + 1
=> P(X <= 14) ≈ 0.593
This means that there is a 59.3% chance that an arbitrarily chosen patient will see the doctor within 14 minutes of the appointment time.
To know more about probability visit:
https://brainly.com/question/11234923
#SPJ1
The distinct lines ABC and deer in the same place tell how Line A. And line B. related to each other justify your answer a ll b,b ll c,c | d

Answers
Line A is perpendicular to D because a is parallel to c and c is perpendicular to d.
How are parallel straight lines related?Parallel lines have the same slope since the slope is like a measure of steepness and since parallel lines are of the same steepness, thus, are of the same slope. Since the given parallel line has equation y = 2x + 2, thus its slope is 2 and thus, the slope of the needed line is 2 too.
WE have been given that a ll b,b ll c,c is perpendicular to d.
Here the line a is parallel to b and b is parallel to c so a must be parallel to c.
As we know that c is perpendicular to d since, a is parallel to c.
Therefore, Line A is perpendicular to D because a is parallel to c and c is perpendicular to d.
Learn more about parallel lines here:
https://brainly.com/question/13857011
#SPJ1
question 3 options: find p(z < -1.57). round answer to 4 decimal places. answer:
Answers
Rounding this answer to four decimal places, we get:
p(z < -1.57) ≈ 0.0589
What is probability?
Probability is a measure or quantification of the likelihood or chance of an event occurring. It represents the ratio of the favorable outcomes to the total possible outcomes in a given situation or experiment. Probability values range from 0 to 1, where 0 indicates an event is impossible and 1 indicates an event is certain to occur.
To find the probability that a standard normal random variable, denoted by Z, is less than a specific value, we can use a standard normal distribution table or a calculator.
Using a standard normal distribution table, we can find the area/probability to the left of a given Z-score.
The Z-score of -1.57 represents the value that is 1.57 standard deviations to the left of the mean (0).
Looking up the Z-score of -1.57 in the standard normal distribution table, we find the corresponding area/probability is 0.0589.
Hence, Rounding this answer to four decimal places, we get:
p(z < -1.57) ≈ 0.0589
To learn more about decimal places
https://brainly.com/question/20563248
#SPJ4
in a large population, 63 % of the people have been vaccinated. if 4 people are randomly selected, what is the probability that at least one of them has been vaccinated? give your answer as a decimal (to at least 3 places) or fraction.
Answers
The probability of at least one person being vaccinated out of four people chosen at random is 0.30, or 30%, rounded to the nearest hundredths.
What do we mean by probability?Probability is a branch of mathematics that deals with numerical summaries of how likely an event is to occur or how likely a proposition is to be true. The likelihood of an event occurring is a number between 0 and 1, where 0 indicates the event's impossibility and 1 indicates certainty.To find the probability that at least one of them has been vaccinated:
In a huge number, 63% of people are vaccinated, leaving 37% unvaccinated. The point of concern for the probability that at least one of the four randomly selected people has been vaccinated. As a result, we must account for the possibility that one, two, three, or four randomly selected people were vaccinated.We use P(1) for only one person; the same reasoning should apply to other subscripts.
P(1) = (63/100)(37/100)(37/100)(37/100) = 0.03089833P(2) = (63/100)(63/100)(37/100)(37/100) = 0.05094049P(3) = (63/100)(63/100)(63/100)(37/100) = 0.08398297P(4) = (63/100)(63/100)(63/100)(63/100) = 0.13845841Adding all these probabilities given 0.3042802.
As a result, the probability of at least one person being vaccinated out of four people chosen at random is 0.30, or 30%, rounded to the nearest hundredths.
Know more about probability here:
https://brainly.com/question/24756209
#SPJ4
John has a bag of marbles. He gives away 3/4 of the marbles to his friend. Later, he receives another bag containing 2/4 of the original number of marbles. How many marbles does John have now?
Answers
Answer:
Total is 3
Step-by-step explanation:
AI-generated answer
Let's start by finding out how many marbles John had initially. We can do this by using the information given in the problem.
Let the original number of marbles be x.
John gave away 3/4 of his marbles, which means he has 1/4 of the original number of marbles left. We can express this as:
1/4 x = the number of marbles John has left
If we solve for x, we get:
4/1 * 1/4 x = 4/1 * the number of marbles John has left
x = 4 * the number of marbles John has left
Now we know that John had 4 times the number of marbles he has left.
Next, John receives another bag of marbles containing 2/4 (which is the same as 1/2) of the original number of marbles.
We can express this as:
1/2 x = the number of marbles in the new bag
To find the total number of marbles John has now, we can add the number of marbles he has left to the number of marbles in the new bag:
Total number of marbles = the number of marbles John has left + the number of marbles in the new bag
Total number of marbles = 1/4 x + 1/2 x
Total number of marbles = (1/4 + 1/2) x
Total number of marbles = (3/4) x
We know that x = 4 times the number of marbles John has left, so we can substitute this into the equation:
Total number of marbles = (3/4) * 4 * the number of marbles John has left
Total number of marbles = 3 * the number of marbles John has left
Therefore, the total number of marbles John has now is 3 times the number of marbles he has left.
Tell me in the commets if you didn't understand a word or something in the equation. :)
Find the area of the shaded region. Use π = 3.14.

Answers
The area of the shaded region is,
⇒ 9.76 cm²
We have to given that;
Side of a square = 8 cm
Hence, We get;
Area of square = 8²
= 64 cm²
And, Area of circle = πr²
= 3.14 × 4²
= 50.24 cm²
Thus, The area of the shaded region is,
⇒ 64 - 50.24
⇒ 9.76 cm²
Therefore, The area of the shaded region is,
⇒ 9.76 cm²
Learn more about the circle visit:
https://brainly.com/question/24810873
#SPJ1
