Someone please help me

There are 30 dogs in the store, and 12 cats.

Let's call the number of dogs in the store "x".

Since the sum of the number of dogs and cats is 42, we know that:

x + (x - 18) = 42

Expanding and solving for x:

2x - 18 = 42

2x = 60

x = 30

So there are 30 dogs in the store, and (30 - 18) = 12 cats.

Read more about equations at

https://brainly.com/question/2972832

#SPJ1

Answer:

32%

Step-by-step explanation:

703/2226=32%

Answer: 0.25

Step-by-step explanation:

Substituting into the slope formula, the slope is \(\frac{-4-(-2)}{-2-6}=0.25\)

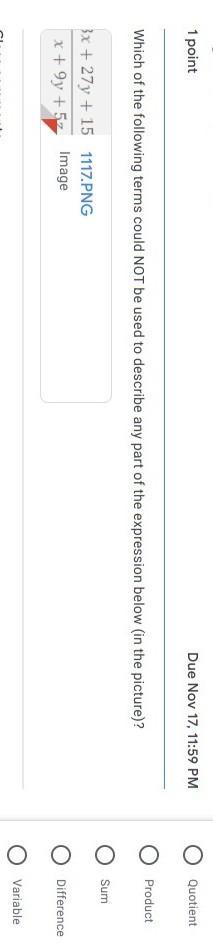
Answer: sum

Step-by-step explanation:

Answer:

sum

Hope this helped!

Have an amazing day!

First let's calculate the number of students who will buy lunch 5 times next week and it is given by:-

So 175 students will buy lunch 5 times.

Similarly let's find number of students who will buy lunch 4 times

75 students will buy 4 times

Similarly on calculation we get 50 students will buy 3 times, 50 students will buy 2 times , 90 students will buy 1 time.

So total number of lunches that will be sold will be

So total 1,515 lunches will be sold .Hence the correct option is (A).

There are 45 possible 4-digit strings with exactly two zeros.

When solving for the number of 4-digit strings with exactly two zeros, there are different approaches to this problem.

One method is to use the combination formula or C(n,r), where n represents the total number of digits and r is the number of zeros to be chosen for the 4-digit string.

Combination formula

C(n,r) = n!/[r!(n - r)!]

Applying this formula, there are 10 digits to choose from and we want exactly two of them to be zeros, so r = 2.

We then substitute these values into the formula:

C(10,2) = 10!/[2!(10 - 2)!]C(10,2) = 45

Learn more about combinations at

https://brainly.com/question/20211959

#SPJ11

Answer:

$1,555.06

Step-by-step explanation:

2. Using proportion, the value of x = 38, the length of FC = 36 in.

3. Applying the angle bisection theorem, the value of x = 13. The length of CD = 39 cm.

The Angle Bisector Theorem states that in a triangle, an angle bisector divides the opposite side into segments that are proportional to the lengths of the other two sides of the triangle.

2. The proportion we would set up to find x is:

(x - 2) / 4 = 27 / 3

Solve for x:

3 * (x - 2) = 4 * 27

3x - 6 = 108

3x = 108 + 6

Simplifying:

3x = 114

x = 114 / 3

x = 38

Length of FC = x - 2 = 38 - 2

FC = 36 in.

3. The proportion we would set up to find x based on the angle bisector theorem is:

13 / 3x = 7 / (2x - 5)

Cross multiply:

13 * (2x - 5) = 7 * 3x

26x - 65 = 21x

26x - 21x - 65 = 0

5x - 65 = 0

5x = 65

x = 65 / 5

x = 13

Length of CD = 3x = 3(13)

CD = 39 cm

Learn more about Angle Bisector Theorem on:

https://brainly.com/question/30459648

#SPJ1

Answer: Rs 1469

Step-by-step explanation:

Coat of item = RS 1300

Value added tax = 13%

The price of the item will then be calculated as:

= 1300 + (1300 × 13%)

= 1300 + (1300 × 0.13)

= 1300 + 169

= Rs 1469

The one-sample z-statistic for evaluating the hypothesis that unvaccinated people get COVID-19 is not 0.03 is -85.7. This statistic tested the hypothesis that unvaccinated people do not get COVID-19 at 0.03%.

In order to compute the one-sample z-statistic, we must first do a comparison between the observed proportion of COVID-19 instances in the placebo group and the expected proportion of 0.03. (p - p0) / [(p0(1-p0)) / n is the formula for the one-sample z-statistic. In this formula, p represents the actual proportion, p0 represents the predicted proportion, and n represents the sample size.

The observed proportion of COVID-19 instances among those who received the placebo is 162/18325 less than 0.0088. According to the received wisdom, the proportion that should be anticipated is 0.03. The total number of people sampled is 18325. After entering these numbers into the formula, we receive the following results:

z = (0.0088 - 0.03) / √[(0.03(1-0.03)) / 18325] ≈ (-0.0212) / √[(0.0291) / 18325] ≈ -85.7

As a result, the value of the z-statistic for just one sample is about -85.7. This demonstrates that the observed proportion of COVID-19 cases in the unvaccinated population is significantly different from the expected proportion of COVID-19 cases in that population.

Learn more about z-statistic here:

https://brainly.com/question/30904553

#SPJ11

Yes. A leg of a right triangle can indicate the distance that separates two vertical or horizontal points, and the hypotenuse can represent the distance between two non-vertical or non-horizontal points.

We can use this theorem to calculate the distances between two locations on a coordinate grid. Consider the following example using the points:

( 3, 4 ) and ( − 2, 1 )

We can see how to make a right triangle with the hypotenuse as that of the line connecting these two spots. A right angle is formed at the coordinates ( 3, 1), where the vertical line from ( 3, 4 ) and the horizontal line from ( 2, 1 ) intersect.

To learn more about the distance between any two points, use the link below.

https://brainly.com/question/20436215?referrer=searchResults

#SPJ4

The connection string for SQL Server using Windows Authentication is as follows:

Server=myServerAddress;Database=myDataBase;Trusted_Connection=True;

Specify the server address in the format "Server=myServerAddress". Replace "myServerAddress" with the name or IP address of the SQL Server instance you want to connect to.

Specify the name of the database you want to connect to in the format "Database=myDataBase". Replace "myDataBase" with the name of the database.

Use Windows Authentication by setting "Trusted_Connection=True". This means that the user running the application is authenticated using their Windows credentials, rather than a SQL Server login.

Use semicolons (;) to separate the different parts of the connection string.

Using Windows Authentication is a more secure and convenient way to connect to a SQL Server database, as it eliminates the need to store and manage login credentials in the application.

For more questions like  SQL Server click the link below:

https://brainly.com/question/30036127

#SPJ4

Answer:

b=   -1/2 a + 15

Step-by-step explanation:

isolate 2B, Take A to the other side and it will become negative. divide all by 2 because of 2B so we can get rid of 2. and that's all

Answer:

B

Step-by-step explanation:

a. When the population standard deviation σ = 15, the population mean μ is approximately 168.2

b. When the population standard deviation σ = 25, the population mean μ is approximately 182

c. When the population mean μ = 136, the population standard deviation σ is approximately 10.94

d. When the population mean μ = 128, the population standard deviation σ is approximately 17.19

To solve this problem, convert the given probability to a z-score and using the z-score formula to solve for the unknown variable.

Given P(X > 150) = 0.10 and σ = 15,

z = (150 - μ) / σ = (150 - μ) / 15

Using a standard normal distribution table, the z-score corresponding to a probability of 0.10 is approximately -1.28.

Thus,

-1.28 = (150 - μ) / 15

Solving for μ,

μ = 150 - (-1.28) * 15 = 168.2

population mean μ is approximately 168.2 when the population standard deviation σ = 15.

Similarly,

z-score corresponding to P(X > 150) = 0.10 when σ = 25 as:

z = (150 - μ) / σ = (150 - μ) / 25

Using a standard normal distribution table, the z-score corresponding to a probability of 0.10 is approximately -1.28.

Thus,

-1.28 = (150 - μ) / 25

Solving for μ, we get:

μ = 150 - (-1.28) * 25 = 182

Therefore, the population mean μ is approximately 182 when the population standard deviation σ = 25.

Also,

Given μ = 136 and using the z-score formula

z = (150 - 136) / σ = 14 / σ

Using a standard normal distribution table, the z-score corresponding to a probability of 0.10 is approximately 1.28.

Thus,

1.28 = 14 / σ

Solving for σ, we get:

σ = 14 / 1.28 = 10.94

Therefore, the population standard deviation σ is approximately 10.94 when the population mean μ = 136.

Lastly,

Given μ = 128 and using the z-score formula,

z = (150 - 128) / σ = 22 / σ

Using a standard normal distribution table, the z-score corresponding to a probability of 0.10 is approximately 1.28.

Thus,

1.28 = 22 / σ

Solving for σ, we get:

σ = 22 / 1.28 = 17.19

Therefore, the population standard deviation σ is approximately 17.19 when the population mean μ = 128.

Learn more on population mean on https://brainly.com/question/29885712

#SPJ4

Answer:

\(m = \frac{1}{2}\)

Step-by-step explanation:

Two points are ( 8, 0 ) and  (0 , - 4)

              \(slope \ , \ m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{-4 -0}{0-8}=\frac{-4}{-8} = \frac{1}{2}\)

Answer:

978 square inches

Step-by-step explanation:

The derivative of abs(x-8) is equal to 1 if x is greater than or equal to 8, and -1 if x is less than 8.

The absolute value function is defined as |x| = x if x is greater than or equal to 0, and |x| = -x if x is less than 0. The derivative of a function is a measure of how much the function changes as its input changes. In this case, the input to the function is x, and the output is the absolute value of x.

If x is greater than or equal to 8, then the absolute value of x is equal to x. The derivative of x is 1, so the derivative of the absolute value of x is also 1.

If x is less than 8, then the absolute value of x is equal to -x. The derivative of -x is -1, so the derivative of the absolute value of x is also -1.

Therefore, the derivative of abs(x-8) is equal to 1 if x is greater than or equal to 8, and -1 if x is less than 8.

Learn more about absolute value function here:

brainly.com/question/28478005

#SPJ11

Answer:

0.4 cups per cup of broth

Step-by-step explanation:

14 cups of water/35 cups of broth

This is the same as 14 divided by 35

14 divided by 35 is 0.4

The diver's velocity during the first 2 sec of fall using the modified Euler method with Ar= 0.2 is 62.732 mph.

Given data: Initial velocity, u = 0 ft/sec

Acceleration, a = g = 32.2 ft/sec²

The maximum rate of fall, vmax = 80 mph

Time, t = 2 seconds

Air resistance constant, Ar = 0.2

We are supposed to determine the sky diver's velocity during the first 2 seconds of fall using the modified Euler method.

The governing equation for the velocity of the skydiver is given by the following:

ma = -m * g + k * v²

where, m = mass of the skydive

r, g = acceleration due to gravity, k = air resistance constant, and v = velocity of the skydiver.

The equation can be written as,

v' = -g + (k / m) * v²

Here, v' = dv/dt = acceleration

Hence, the modified Euler's formula for the velocity can be written as

v1 = v0 + h * v'0.5 * (v'0 + v'1)

where, v0 = 0 ft/sec, h = 2 sec, and v'0 = -g + (k / m) * v0² = -g = -32.2 ft/sec²

As the initial velocity of the skydiver is zero, we can write

v1 = 0 + 2 * (-32.2 + (0.2 / 68.956) * 0²)0.5 * (-32.2 + (-32.2 + (0.2 / 68.956) * 0.5² * (-32.2 + (-32.2 + (0.2 / 68.956) * 0²)))

v1 = 62.732 mph

Therefore, the skydiver's velocity during the first 2 seconds of fall using the modified Euler method with Ar= 0.2 is 62.732 mph.

To know more about the Euler method visit:

https://brainly.com/question/32564424

#SPJ11

The error in the calculation is the incorrect integration limits chosen for finding the area bounded by the graph. The correct solution involves finding the integral of the absolute value of the function over the appropriate interval.

The given solution assumes that the area can be found by integrating the function cos(2πx) from a to π, where a is an arbitrary constant. However, this is not a correct approach.

To solve the problem correctly, we need to consider the behavior of the function cos(2πx) over the interval of interest. The function oscillates between 1 and -1 as x varies from 0 to 1, completing one full period. The area bounded by the graph and the x-axis can be calculated by taking the integral of the absolute value of the function over this interval.

Using the correct integration limits, the area can be calculated as follows:

Area = ∫[0,1] |cos(2πx)| dx

The absolute value ensures that we consider the positive area above the x-axis and the negative area below it. Evaluating this integral yields the correct solution for the total area bounded by the graph.

Learn more about x-axis here: https://brainly.com/question/2491015

#SPJ11

<3<3<3<3<3<3<3<3<3<3<3<3<3<3<3<3<3<3<3<3<3<3<3

Answer:

Yes, it is!!!

<3<3<3<3<3<3<3<3<3<3<3<3<3<3<3<3<3<3<3<3<3<3<3

From the given information, cholesterol level X follows the N(222, 37) distribution.

The probability of having borderline high cholesterol (between 200 and 240 mg/dl) can be calculated by using the z-score formula as follows:

z = (x - μ) / σ

For lower limit x1 = 200, z1 = (200 - 222) / 37 = -0.595

For upper limit x2 = 240, z2 = (240 - 222) / 37 = 0.486

The probability of having borderline high cholesterol (between 200 and 240 mg/dl) can be computed as

P(200 ≤ X ≤ 240) = P(z1 ≤ Z ≤ z2) = P(Z ≤ 0.486) - P(Z ≤ -0.595) = 0.683 - 0.277 = 0.406

In this population, 90% of men have a cholesterol level that is at most X90.The z-score corresponding to a cholesterol level of X90 can be calculated as follows:

z = (x - μ) / σ

Since the z-score separates the area under the normal distribution curve into two parts, that is, from the left of the z-value to the mean, and from the right of the z-value to the mean.

So, for a left-tailed test, we find the z-score such that the area from the left of the z-score to the mean is 0.90.

By using the standard normal distribution table,

we get the z-score as 1.28.z = (x - μ) / σ1.28 = (X90 - 222) / 37X90 = 222 + 1.28 × 37 = 274.36 ≈ 274

The cholesterol level of 90% of men in this population is at most 274 mg/dl.

The distributions that we can consider to be approximately normal are the sampling distribution of mean BMI for random samples of 60 adults and the sampling distribution of mean BMI for random samples of 9 adults.

The reason for considering these distributions to be approximately normal is that according to the Central Limit Theorem, if a sample consists of a large number of observations, that is, at least 30, then its sample mean distribution is approximately normal.

To know more about BMI visit:

https://brainly.com/question/11450847

#SPJ11

Using the Pythagorean theorem, the length of the water slide is approximately 24.7 meters.

What is the Pythagorean theorem?

The Pythagorean theorem is a fundamental idea in geometry that asserts that the square of the length of the hypotenuse (the side opposite the right angle) in a right triangle= the sum of the squares of the other two sides. In equation form, it is as follows:

a² + b² = c²

Now,

Using the Pythagorean theorem, we can find the length of the water slide as follows:

Length of the slide = √(23² + 9²) meters

Length of the slide = √(529 + 81) meters

Length of the slide = √610 meters

Length of the slide ≈ 24.7 meters (rounded to the nearest tenth)

Therefore, the length of the water slide is approximately 24.7 meters.

To know more about Pythagorean theorem visit the link

brainly.com/question/343682

#SPJ1

The area of the given  isosceles triangle is 480 square units.

Isosceles triangle:

An isosceles triangle is a triangle with two sides of equal length. Let's do a little activity to understand this better. Take a square piece of paper and fold it in half. Draw a line from the folded top corner to the bottom edge (see image below). Open the sheet and you will see a triangle. Mark the triangle vertices as O, D, C. Then measure OD and OC. Repeat this activity at different scales and observe patterns. We can see that OD and OC are always the same. A triangle with two equal sides is called an isosceles triangle.

Given,

base (b) = 20 units and

height (h) = 120 units.

The formula to calculate the area is 1/2 × b × h square units.

By substituting the values, we get

⇒ Area = 1/2 × 20 × 120

            = 480 unit Squares

Therefore, the area of the given  isosceles triangle is 96 square units.

Learn more about Isosceles triangle:

https://brainly.com/question/2456591

#SPJ4

To determine the percentage of scores that fall between 52 and 62, we can calculate the z-scores for these values and use the standard normal distribution table or a statistical calculator.

First, we calculate the z-score for 52 using the formula:

z = (x - μ) / σ

where x is the value (52), μ is the mean (48), and σ is the standard deviation (7).

z = (52 - 48) / 7

z = 4 / 7

z ≈ 0.57

Next, we calculate the z-score for 62:

z = (62 - 48) / 7

z = 14 / 7

z = 2

Now, we can use the standard normal distribution table or a statistical calculator to find the percentage of scores between these z-scores.

Using the standard normal distribution table, we can look up the area/probability corresponding to each z-score.

For z = 0.57, the area/probability is approximately 0.7123.

For z = 2, the area/probability is approximately 0.9772.

To find the percentage between these two z-scores, we subtract the area/probability corresponding to the lower z-score from the area/probability corresponding to the higher z-score:

Percentage = (0.9772 - 0.7123) * 100

Percentage ≈ 26.49

Therefore, approximately 26.49% of scores fall between 52 and 62. Since none of the given answer choices match this value, it appears that the provided answer choices do not include the correct option.

To know more about  calculator refer here

https://brainly.com/question/30151794#

#SPJ11

Step-by-step explanation:

The upstream speed is S / t₁, and the downstream speed is S / t₂.

If we say f is the speed of the fish in calm water, and r is the speed of the river, then:

f − r = S / t₁

f + r = S / t₂

If we say T is the time it takes to cross the river, then the speed perpendicular to the river is ℓ/T, the speed parallel to the river is r, and the overall speed is f.

Using Pythagorean theorem:

f² = (ℓ/T)² + r²

f² − r² = (ℓ/T)²

(f − r) (f + r) = (ℓ/T)²

(S / t₁) (S / t₂) = (ℓ/T)²

S² / (t₁ t₂) = (ℓ/T)²

(t₁ t₂) / S² = (T/ℓ)²

√(t₁ t₂) / S = T/ℓ

T = ℓ√(t₁ t₂) / S