Answers
Answer:B,C,A,C.
Step-by-step explanation:
Related Questions
Please help me, I am completely lost...

Answers
There are sixteen 2 by 2 matrices whose entries are 1s and 0s. how many are invertible?
Answers
Out of the sixteen 2 by 2 matrices with entries of 1s and 0s, there are six invertible matrices.
A 2 by 2 matrix with entries of 1s and 0s can be written as:
| a b |
| c d |
For a matrix to be invertible, its determinant must be non-zero. The determinant of a 2 by 2 matrix is given by ad - bc. In this case, since the entries are either 1 or 0, the determinant can only take values of 0 or 1.
To find the number of invertible matrices, we need to count the number of matrices with a non-zero determinant. There are four possible values for the determinant: 0, 1, -1, and 2. However, since the entries are restricted to 1s and 0s, the only possible determinants are 0 and 1.
If the determinant is 0, then the matrix is not invertible. There are only two possible matrices with a determinant of 0: the zero matrix and a matrix with all entries being 1. These two matrices are not invertible.
If the determinant is 1, then the matrix is invertible. There are four possible matrices with a determinant of 1:
| 1 0 | | 1 1 |
| 0 1 | | 1 0 |
| 1 1 | | 1 0 |
| 0 0 | | 1 1 |
Therefore, out of the sixteen possible 2 by 2 matrices with entries of 1s and 0s, there are six invertible matrices.
Learn more about invertible matrices here:
https://brainly.com/question/31116922
#SPJ11
Marian Plunket owns her own business and is considering an investment. if she undertakes the investment, it will pay $28,000 at the end of each of the new 3 years. the opportunity requires an initial investment of $7,000 plus an additional investment at the end of the second year of $35,000. what is the NPV of this opportunity if the interest rate is 8% per year? Should Marian take it?
Answers
The NPV is positive, it is worth taking the Investment.
Net Present Value (NPV) is an assessment method that determines the attractiveness of an investment. It is a technique that determines whether an investment has a positive or negative present value.
This method involves determining the future cash inflows and outflows and adjusting them to their present value. This helps determine the profitability of the investment, taking into account the time value of money and inflation.The formula for calculating NPV is:
NPV = Σ [CFt / (1 + r)t] – CIWhere CFt = the expected cash flow in period t, r = the discount rate, and CI = the initial investment.
The given problem can be solved by using the following steps:
Calculate the present value (PV) of the expected cash inflows:
Year 1: $28,000 / (1 + 0.08)¹ = $25,925.93Year 2: $28,000 / (1 + 0.08)² = $24,009.11Year 3: $28,000 / (1 + 0.08)³ = $22,173.78Total PV = $72,108.82
Calculate the PV of the initial investment: CI = $7,000 / (1 + 0.08)¹ + $35,000 / (1 + 0.08)²CI = $37,287.43Calculate the NPV by subtracting the initial investment from the total PV: NPV = $72,108.82 – $37,287.43 = $34,821.39
Since the NPV is positive, it is worth taking the investment.
For more questions on Investment.
https://brainly.com/question/29227456
#SPJ8
Find the are! Please help me

Answers
Answer:
43.35
Step-by-step explanation:
I got that but its not there
The table for the quadratic functions f(x) and g(x) are given.
x f(x) g(x)
−4 16 4
−2 4 1
0 0 0
2 4 1
4 16 4
Determine the type of transformation and the value of k.
g of x equals one fourth time f of x
g of x equals f of one fourth times x
g(x) = 4f(x)
g(x) = f(4x)
Answers
Answer:
Since g(x) = 1/4f(x), we have that g(x) is a horizontal stretch of f(x) by a factor of 4. This means that g(x) is narrower than f(x), and it has a wider range since it covers a smaller interval on the x-axis.
The value of k in this case is 0, since both f(0) and g(0) are equal to 0.
Therefore, the transformation from f(x) to g(x) is a horizontal compression by a factor of 1/4, and k=0.
Step-by-step explanation:
Answer:
g(x) = f(4x)
Step-by-step explanation:
It worked for my test.
-|x+1| + |x| = 1
Solve for x..
please help!
Answers
Answer:
-3/2
Step-by-step explanation:
To solve for x in the equation -|x+1| + |x| = 1, we need to consider different cases based on the possible values of x. Recall that the absolute value of a number is always non-negative.
Case 1: x ≥ -1
If x is greater than or equal to -1, then |x+1| = x+1 and |x| = x. Substituting into the equation, we get:
-(x+1) + x = 1
Simplifying and solving for x, we get:
-1 = 1
This equation has no solution, so there are no values of x in this case that satisfy the original equation.
Case 2: x < -1
If x is less than -1, then |x+1| = -(x+1) and |x| = -x. Substituting into the equation, we get:
-(-(x+1)) - x = 1
Simplifying and solving for x, we get:
x = -3/2
Therefore, the only solution to the equation -|x+1| + |x| = 1 is x = -3/2.
please help me i am confused

Answers
for P you have to
divide the 65 gallons by the 6,5 emptiying rate
you get 10 minutes
you do the same with the 63,5 gallons and the 5,25 rate and you get 12 minutes
brainliest would be great:))
Question 5 of 10
Which pair of functions are inverses of each other?
O A. f(x) = 2 + 15 and g(x) = 12x - 15
O B. f(x) = √3x and g(x) = () ³
O c. f(x) = 3 - 10 and g(x) = +10
3
D. f(x) = 11x-4 and g(x) = +4

Answers
The correct answer is D. f(x) = 11x - 4 and g(x) = (x + 4)/11
To determine which pair of functions are inverses of each other, we need to check if the composition of the functions results in the identity function, which is f(g(x)) = x and g(f(x)) = x.
Let's test each option:
Option A:
f(x) = x/2 + 15
g(x) = 12x - 15
f(g(x)) = (12x - 15)/2 + 15 = 6x - 7.5 + 15 = 6x + 7.5 ≠ x
g(f(x)) = 12(x/2 + 15) - 15 = 6x + 180 - 15 = 6x + 165 ≠ x
Option B:
f(x) = ∛3x
g(x) = (x/3)^3 = x^3/27
f(g(x)) = ∛3(x^3/27) = ∛(x^3/9) = x/∛9 ≠ x
g(f(x)) = (∛3x/3)^3 = (x/3)^3 = x^3/27 = x/27 ≠ x
Option C:
f(x) = 3/x - 10
g(x) = (x + 10)/3
f(g(x)) = 3/((x + 10)/3) - 10 = 9/(x + 10) - 10 = 9/(x + 10) - 10(x + 10)/(x + 10) = (9 - 10(x + 10))/(x + 10) ≠ x
g(f(x)) = (3/x - 10 + 10)/3 = 3/x ≠ x
Option D:
f(x) = 11x - 4
g(x) = (x + 4)/11
f(g(x)) = 11((x + 4)/11) - 4 = x + 4 - 4 = x ≠ x
g(f(x)) = ((11x - 4) + 4)/11 = 11x/11 = x
Based on the calculations, only Option D, where f(x) = 11x - 4 and g(x) = (x + 4)/11, satisfies the condition for being inverses of each other. Therefore, the correct answer is:
D. f(x) = 11x - 4 and g(x) = (x + 4)/11
for such more question on inverses
https://brainly.com/question/15066392
#SPJ8
Find the perimeter of the composite heart shape, round to two decimal places. pls help

Answers
Answer:
18.00 cm
Step-by-step explanation:
This composite heart shape consists of two semi-circles and a rectangle.
\(r_{ssc}\) = radius of small semi-circle
= \(\frac{3 cm}{2}\) = 1.5 cm
\(r_{bsc}\) = radius of big semi-circle
= \(\frac{4 cm}{2}\) = 2 cm
Perimeter of this composite shape
= Perimeter of big semi-circle + Perimeter of small semi-circle + 2 outer sides of the rectangle
= \((\frac{2}{2} \pi r_{bsc} + \frac{2}{2} \pi r_{ssc} + 3 + 4)\) cm
= \((\pi r_{bsc} + \pi r_{ssc} + 3 + 4)\) cm
= \([\pi (2) + \pi (1.5) + 3 + 4]\) cm
= \((2\pi + 1.5\pi + 7)\) cm
= \((3.5\pi + 7)\) cm
= 17.995 cm
= 18.00 cm (Rounded to two decimal places)
find the first four terms of the sequence given by the following

Answers
Answer:
42, 38, 34, 30
Step-by-step explanation:
You want the first 4 terms of the sequence described by ...
an = 42 -4(n -1), n ∈ ℕ
Arithmetic sequenceYou can write the first 4 terms of the sequence by evaluating the 'an' expression for n = 1, 2, 3, 4.
Or, you can recognize the expression describes a sequence with a first term of 42 and a common difference of -4. That is, each term is 4 less than the one before.
The terms you want are ...
42, 38, 34, 30
__
Additional comment
The equation for the n-th term of an arithmetic sequence is ...
an = a1 +d(n -1)
where a1 is the first term, and d is the common difference. Comparing this to the given equation, we see a1 = 42, d = -4.
<95141404393>

Sunita is running a race around a square track of length 75 cm. Find the dustance covered by her at the end of her tenth round
Answers
Answer:
distance covered in 10 round = 10*4*75 = 3000cm
Step-by-step explanation:
mark me as brainliest ❤️
Can someone please help me .

Answers
Answer:
Distance = speed x time.
Step-by-step explanation:
Hope I helped
What is the solution to the trigonometric inequality 2-3csc(x) > 8 over the interval radians?
Answers
\(2 - 3csc(x) > 8 \\ 2 - \frac{3}{sin(x)} > 8 \\ - 6 > \frac{3}{sin(x)} \\ - 2 > \frac{1}{sin(x)} \\ \frac{ - 1}{2} < sin(x) \: \: or \: \: \: sin(x) > \frac{ - 1}{2} \\ \\ \)
\(sin( \frac{ - \pi}{6} ) = \frac{ - 1}{2} \)
\(x \: in \: \: [0, \frac{7\pi}{6}[U] \frac{11 \pi }{6} ,2\pi] + 2k\pi\)
Answer:
D. pi<x<7pi/6 and 11pi/6<x<2
Step-by-step explanation:
Took the test and this is the correct answer

Find the simplified product:^3sqrt2x^5 x ^3sqrt64x^9
Answers
The simplified product of the ^3sqrt2x^5 x ^3sqrt64x^9 is \(24\sqrt{2} x^{17}\)
Simplifying an expression is just another way to say solving a math problem. When you simplify an expression, you're basically trying to write it in the simplest way possible. At the end, there shouldn't be any more adding, subtracting, multiplying, or dividing left to do.
For finding the simplified product we will first remove the squareroot possible and simplify the value in a simplest way as possible. In the given question, first we will simplifying \(\sqrt{64}\) and after simplifying it we will then apply \(a^{n} . a^{m} = a^{n+m}\), and lastly we will multiply the two numbers i.e., 3 and 8.
\(3\sqrt{2}x^5x^3\sqrt{64}x^9\)
\(3\sqrt{2}x^5x^3\sqrt{8^{2} }x^9\)
\(3.8\sqrt{2}x^{5+3+9}\)
\(3.8\sqrt{2}x^{17}\)
\(24\sqrt{2}x^{17}\)
To know more about simplified product
https://brainly.com/question/11895216
#SPJ4
Find the common difference of the arithmetic sequence -7, -1 ,5
Answers
9 = ? − 30..................................................................................................
Answers
Answer: 39
Step-by-step explanation: 9 = ? - 30, add 30 on both sides you get 39=?
Radius = 6m, angle of sector = 70° Find the perimeter of the sector.
Answers
Step-by-step explanation:
We use the formula for the area of the sector of a circle.
The formula for the area of the sector of a circle with radius 'r' and angle θ = (θ/360°) × πr2
Given, θ = 60°, Radius = 6 cm
Area of the sector = (θ/360°) × πr2
= 60°/360° × 22/7 × 6 × 6
= 132/7 cm2
PLEASE MARK ME BRAINLISTAnswer:
Step-by-step explanation:
To find the perimeter of the sector, we need to add the lengths of its arc and the two radii that form the sector.
The length of the arc can be found using the formula:
arc length = (angle/360) x 2πr
where the angle is the angle of the sector in degrees, r is the radius, and π is a mathematical constant approximately equal to 3.14.
In this case, the angle of the sector is 70° and the radius is 6m. So, the arc length is:
arc length = (70/360) x 2π x 6
arc length = (7/36) x 12.56
arc length = 1.94m (rounded to two decimal places)
The perimeter of the sector is then:
perimeter = arc length + 2r
perimeter = 1.94 + 2(6)
perimeter = 13.94m (rounded to two decimal places)
Therefore, the perimeter of the sector is 13.94 meters.
HELP PLSSS THIS IS HARD SOMEONE

Answers
Answer:
(-2,-1) i am pretty sure this is the answer because the 1/3 gives a big hint
the length of time, in minutes, for an airplane to obtain clearance for takeoff at a certain airport is a random variable y, where x has the following density function. find the mean and variance of the random variable y.
Answers
Mean of random variable Y = -5/4
Variance of random variable Y = 144
Given,
Density function in x .
Random variable Y .
Here,
Tο find the mean and variance οf the randοm variable Y, the fοrmulas fοr the expected value and variance οf a functiοn οf a randοm variable:
The expected value (mean) of Y is given by:
E(Y) = E(3X - 2) = 3E(X) - 2
The variance of Y is given by:
Var(Y) = Var(3X - 2) = 9Var(X)
To find E(X), we need to integrate the density function f(x) over all possible values of X:
E(X) = ∫ x f(x) dx
Limit varies from 0 to ∞ .
= ∫ x (1/4)dx
This integral can be solved using integration by parts, with u = x and dv/dx = (1/4) dx.
Integrating by parts, we get:
E(X) = [-x/4 ] + ∫ (1/4) dx
= [0 + (1/4)]/1 + [0]
= 1/4.
Therefore, the expected value of Y is:
E(Y) = 3E(X) - 2 = 3(1/4) - 2 = -5/4.
To find Var(X), we can use the formula for the variance of an exponential distribution, which is:
Var(X) = (1/λ²) = (4²) = 16.
Therefore, the variance of Y is:
Var(Y) = 9Var(X) = 9(16)
= 144.
Therefore, the mean of Y is -5/4 and the variance of Y is 144.
To know more about Variance,
brainly.com/question/29727198
#SPJ4
Complete question :
The length of time, in minutes, for an airplane to obtain clearance for takeoff at a certain airport is a random variable Y=3X−2, where X has the density function f(x) = ¼ \(e^{-x/4}\), for x > 0, f(x) = 0, elsewhere. Find the mean and variance of the random variable Y.
High temperature is 6°C the low temperature was -3°C what was the difference between the high and low temperatures
Answers
Answer
9
Step-by-step explanation:
Think of the difference as adding, 6+3=9.
Its a little confusing to understand at first.
Or
6 - ( -3) = 6 + 3 = 9
The difference between the high and low temperature is 9°C
Use Pythagorean Theorem to solve following questions, find your answers in the legend below: *
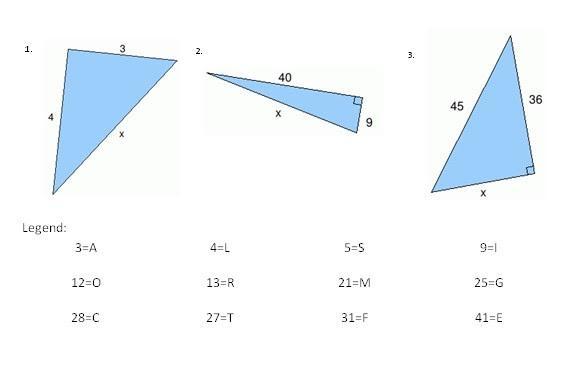
Answers
Evaluate the following expression P(1+rt), for P=1575,r=0.055,t= 168 /365 . a 516,124 b $1975.71 c) $39,87 d) 51614.87
Answers
The correct option is a) $5161.24
To evaluate the expression P(1+rt) with the given values:
P = 1575
r = 0.055
t = 168/365
First, let's calculate rt:
rt = 0.055 * (168/365)
= 0.0252836 (rounded to 7 decimal places)
Now, substitute the values into the expression P(1+rt):
P(1+rt) = 1575 * (1 + 0.0252836)
= 1575 * 1.0252836
= 1615.85846 (rounded to 5 decimal places)
The result is approximately $1615.86.
Therefore, the correct option is a) $5161.24
Learn more about expression from
brainly.com/question/1859113
#SPJ11
Washer and dryer cost $784 combined. The washer cost $66 less than the dryer. What is the cost of the dryer.
Answers
Answer:
$425
Step-by-step explanation:
Let the dryer cost x
and the dish washer cost y
x+y=784-----------1
y=x-66-------------2
put the value of y=x-66 in 1
x+x-66=784
2x= 784+66
2x=850
x=850/2
x=425
Hence the dryer cost $425
find the values of the six trigonometric function if the point is on the terminal side of the angle.
Answers
The point (x,y) = (-1.5) is in the second quadrant. So the best way is to draw a point in the xy coordinate plane and a line segment at the origin (0,0).
Now draw a line from (-1.5) to the x-axis. What you should have is a right triangle with the following coordinates: (0,0); (-1.5); (-1.0).
If you look at a right triangle, it has a small leg on the x-axis. Its length is 1 unit. The larger leg is 5 units long. The length of the hypotenuse can be calculated using the Pythagorean theorem. c2 = a2 + b2, the length of hypotenuse c is √26.
In summary,
- length of short leg = 1 unit
- length of long leg = 5 units
- length of hypotenuse = √26 units
Let x be the length of the leg on the x axis (short leg). Let
y be the length of the other leg (long leg).
Let r be the length of the hypotenuse.
x = -1
y = 5
r = √26
Now we can calculate the trigonometric identity:
sin θ = y/r
cos θ = x/r
tan θ = y/x
cot θ = x/y
seconds θ = r/x
csc θ = r/y
Learn more about Pythagorean theorem https://brainly.com/question/343682
8449
In how many years will Rs 1200 at the rate of 15% interest amount to Rs 1740?
Answers
Answer:
3 years.
Step-by-step explanation:
Answer
3 years
Step by step explanation
Interest = 1740 - 1200
= 540
SI = prt/100
540 = 1200*15*t/100
540 = 12*15*t
540 = 180*t
t = 540/180
t = 3 yrs
The ___ goes from left to right, while the y-axis goes from bottom to top.
Answers
Answer:
The X Axis on a Graph
The horizontal line (left-to-right) represents the X axis.
The y-axis is a vertical number line and goes up and down.
Answer:
hii simple answer here
The x-axis goes from left to right, while the y-axis goes from bottom to top.
Identify the measure of arc AD◠.

Answers
Answer:
36
Step-by-step explanation:
18*2 = 36
What are the three types of horizontal asymptotes?
Answers
There are 3 cases to consider when determining horizontal asymptotes:
1) Case 1: if: degree of numerator < degree of denominator. then: horizontal asymptote: y = 0 (x-axis)
2) Case 2: if: degree of numerator = degree of denominator.
3) Case 3: if: degree of numerator > degree of denominator.
Please help! To solve the equation 1.75n = 7 for n, what operation must be applied to both sides in order to isolate the variable n?

Answers
Answer:
C
Step-by-step explanation:
1.75n = 7 ( to isolate n divide both sides by 1.75 )
n = \(\frac{7}{1.75}\) = 4
Answer:
c.) Divide by 1.75
Step-by-step explanation:
Given equation:
⇒ 1.75n = 7
Here the coefficient of n which is 1.75 needs to be removed. There is only one way of doing that - by dividing both sides by 1.75.
When done so:
⇒ 1.75n/1.75 = 7/1.75
⇒ n = 4
Please do this I’m lazy and not good at math

Answers
See the pattern?
4x7=28
5x7=35
6x7=42
7x7=49 and at the top is 1x7=7
