Solve the right triangle. webassign plot find the length of the side adjacent to the given angle. (round your answer to two decimal places. ) incorrect
Answers
To solve the right triangle and find the length of the side adjacent to the given angle, follow these steps:
1. Identify the angle given in the problem. This angle is often labeled with a Greek letter, such as θ.
2. Determine which side of the triangle is adjacent to the given angle. The side adjacent to an angle is the side that is directly connected to that angle and not the hypotenuse.
3. Use the trigonometric function that involves the angle and the adjacent side. In this case, since we are finding the length of the side adjacent to the angle, we will use the cosine function.
4. Write down the cosine function and plug in the value of the given angle. The cosine function is defined as the ratio of the adjacent side to the hypotenuse. Let's call the length of the adjacent side "a" and the hypotenuse "h". The cosine function can be written as cos(θ) = a/h.
5. Rearrange the equation to solve for the length of the adjacent side (a). Multiply both sides of the equation by h to isolate "a". The equation becomes a = h * cos(θ).
6. Determine the value of the hypotenuse (h) if it is not given in the problem. If the hypotenuse is given, simply use that value.
7. Substitute the values of the hypotenuse (h) and the given angle (θ) into the equation. Multiply the hypotenuse by the cosine of the given angle to find the length of the adjacent side.
8. Round your answer to two decimal places as specified in the problem.
By following these steps, you will be able to find the length of the side adjacent to the given angle in the right triangle.
Learn more about Trigonometry: https://brainly.com/question/13729598
#SPJ11
Related Questions
How many different ways can your write the ratio
of dogs to cats in the pet store if there are 6 cats
and 8 dogs?
Answers
There are infinite many ways to write the ratios of the pets
How to determine the number of waysFrom the question, we have the following parameters that can be used in our computation:
Cats = 6
Dogs = 8
The ratio of dogs to cats in the pet store can be written as:
8:6
To find the different ways to write this ratio, we need to find all the possible equivalent ratios.
We can do this by multiplying or dividing both the proportions by the same number.
For example, if we multiply by 2, we get:
(8 x 2) : (6 x 2) = 16:12
This is an equivalent ratio
We can also divide by a common factor, such as 2:
8 ÷ 2 : 6 ÷ 2 = 4:3
Read more about ratios at
https://brainly.com/question/12024093
#SPJ1
Find the area of the figure shown. Round to the nearest tenth if necessary.

Answers
Answer:
25.5in²
Step-by-step explanation:
A trapezoid is a convex quadrilateral. A trapezoid has at least on pair of parallel sides. the parallel sides are called bases while the non parallel sides are called legs
Characteristics of a trapezoid
It has 4 vertices and edges
If both pairs of its opposite sides of a trapezoid are parallel, it becomes a parallelogram
Area of a trapezoid = (1/2) x (sum of the lengths of the parallel sides) x height
1/2 x (6 + 11) x 3 = 25.5 in²
the tenth is the first number after the decimal place. To convert to the nearest tenth, look at the number after the tenth (the hundredth). If the number is greater or equal to 5, add 1 to the tenth figure. If this is not the case, add zero
Calvin evaluated Negative two-thirds times 5 and one-sixth using the steps below. Step 1: Negative two-thirds time (5 + one-sixth) Step 2: (Negative two-thirds + 5) times (Negative two-thirds + one-sixth) Step 3: 4 and one-third times negative one-half Step 4: Negative 2 and one-sixth Which describes Calvin’s error? In step 1, he incorrectly broke up 5 and one-sixth. In step 2, he distributed the Negative two-thirds instead of the 5. In step 2, he confused the multiplication and addition signs. In step 3, he computed the addition and multiplication incorrectly.
Answers
Answer:
In step 2, he confused the multiplication and addition signs
Step-by-step explanation:
Answer:
In step 2, he confused the multiplication and addition signs.
Step-by-step explanation:
the two dice are rolled and the sum of the results is calculated. what is the probability of the sum equaling 5?
Answers
The probability of the sum equaling 5 is 1/9
How to determine the probability of the sum equaling 5?From the question, we have the following parameters that can be used in our computation:
Rolling two dice
When two dice are rolled, we have
Outcomes = 36
Sum of 5 = 4
using the above as a guide, we have the following:
P = Sum of 5/Outcomes
substitute the known values in the above equation, so, we have the following representation
P = 4/36
Evaluate
P = 1/9
Hence, the probability is 1/9
Read more about probability at
https://brainly.com/question/31649379
#SPJ1
A'B is a translation of AB . Write the translation rule. Image of questions and answers below. POINTS UP FOR GRABS! MATHEMATICS GEOMETRY!
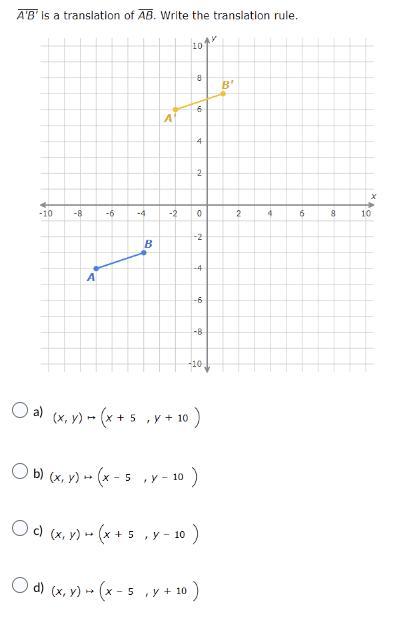
Answers
(x,y)⇒(x+5,y+10) is the translation rule for A'B, which is a translation of AB.
What is translation?A translation is a geometric transformation in Euclidean geometry that moves every point in a figure, shape, or space by the same distance in the same direction. A translation may alternatively be thought of as adding a constant vector to each point or changing the coordinate system's origin. A translation is a sort of transformation that involves sliding each point in a figure the same distance in the same direction. A translation in mathematics moves a form left, right, up, or down but does not turn it. The translated (or picture) shapes appear to have the same size as the original shape, showing that they are congruent. They've just moved in one or more directions.
Here,
A translation is a sort of transformation in which every point in a figure moves the same distance in the same direction. Slides are another term for translations. A translation can be described with words like "moved up 3 and over 5 to the left" or using notation.
The translation rule for A'B is a translation of AB is (x,y)⇒(x+5,y+10).
To know more about translation,
https://brainly.com/question/28830412
#SPJ1
Type the correct answer in each box. Use numerals instead of words. If necessary, use / for the fraction bar(s).
The slope of the line shown in the graph is _____
and the y-intercept of the line is _____ .

Answers
The slope of the line shown in the graph is __2/3__
and the y-intercept of the line is __6___
How to find the slope and the y-intercept?The general linear equation is written as follows:
y = ax + b
Where a is the slope and b is the y-intercept.
On the graph we can see that the y-intercept is y = 6, then we can write the line as:
y = ax + 6
The line also passes through the point (-9, 0), replacing these values in the line we will get:
0 = a*-9 + 6
9a = 6
a = 6/9
a = 2/3
That is the slope.
Learn more about linear equations at:
https://brainly.com/question/1884491
#SPJ1
10.4. RUN #I Let the square wave function f(t), defined below over the domain 0 ≤t≤1₂: >={₁ B f(t)= A for for 1₁ <1≤1₂ 0≤1≤1₁ be a periodic function (f(t) = f(t±nT)), for any integer n, and period T=1₂. Create a plot using Matlab of f(t), using 100 points, over 2 periods for the following functions: (1)fi(t) defined by A-5, B=-5, 12-2 seconds and t₁=1 seconds. (2) f2(1) defined by A-6, B=-3, 12-3 seconds and 11=2 seconds (3) f3(1) defined by A-3, B=0, t2=2 seconds and t₁=1/2 seconds (4) f4 (1) defined by f4(t) = -f(t) (5) fs (1) defined by A-5, B=-3, 1₂2=2 seconds and t₁=1 seconds (6) f6 (1) fi(t) +f 3 (t) (7) fr (t)=f1 (1) *1 (8) fs (t)=f7 (1) + f2 (1)
Answers
Step 1: The plot shows the square wave function f(t) over 2 periods for various functions defined by different values of A, B, and time intervals.
Step 2:
The given question asks us to plot the square wave function f(t) using MATLAB for different variations of the function. Let's analyze each part of the question and understand what needs to be done.
In the first step, we are asked to plot fi(t) defined by A=-5, B=-5, t₁=1 seconds, and 12-2 seconds. This means that for the time interval 0 to 1₁, the function has a value of A=-5, and for the time interval 1₁ to 1₂, the function has a value of B=-5. We need to plot this function using 100 points over 2 periods, which means we will plot the function for the time interval 0 to 2 periods.
In the second step, we are asked to plot f2(t) defined by A=-6, B=-3, t₁=1 seconds, and 12-3 seconds. Similar to the first step, we will plot this function over 2 periods.
In the third step, we have f3(t) defined by A=-3, B=0, t₁=1/2 seconds, and t2=2 seconds. Again, we will plot this function over 2 periods using MATLAB.
In the fourth step, we need to plot f4(t) defined as the negative of the square wave function f(t). This means that for the time interval 0 to 1₁, the function will have a value of -A, and for the time interval 1₁ to 1₂, the function will have a value of -B. We will plot this function over 2 periods.
In the fifth step, we are asked to plot fs(t) defined by A=-5, B=-3, t₁=1 seconds, and 1₂2=2 seconds. Again, we will plot this function over 2 periods.
In the sixth step, we need to plot f6(t) which is the sum of fi(t) and f3(t). We will plot this function by adding the corresponding values of fi(t) and f3(t) at each time point over 2 periods.
In the seventh step, we are asked to plot fr(t) which is the product of f1(t) and the constant 1. This means that the values of f1(t) will remain the same, and we will multiply each value by 1. We will plot this function over 2 periods.
In the eighth and final step, we need to plot fs(t) which is the sum of fr(t) and f2(t). Similar to the previous steps, we will plot this function by adding the corresponding values of fr(t) and f2(t) at each time point over 2 periods.
Step 3:
The given question requires us to plot the square wave function f(t) with different variations. Each variation involves specific values of A and B, as well as different time intervals. By following the instructions, we can create the desired plots using MATLAB and visualize the resulting waveforms.
The first step involves plotting fi(t) with A=-5, B=-5, t₁=1 second, and 12-2 seconds. This means that the function will have a value of -5 for the first half of the time interval and -5 for the second half. By plotting this waveform over 2 periods using 100 points, we can observe the square wave with the given characteristics.
In the second step, we plot f2(t) with A=-6, B=-3,
Learn more about: square wave function
brainly.com/question/31829734
#SPJ11
the code below a: { int a = 1; b:{ int b = 2; int c = 2; c: { int c = 3; int d; d = a b c; write(d); } d: { int e; e = a b c; write(e); } } } variable c in block d has the value
Answers
The value of variable c in block d is 2.
In the given code, there are multiple nested blocks with variables a, b, c, and d. The variable c appears in two different scopes: one within block b and another within block c.
When the code reaches the innermost block c, a new variable c is declared with a value of 3. This innermost c variable shadows the outer c variable, which has a value of 2 in block b.
Inside the innermost block c, the value of d is assigned as the concatenation of variables a, b, and c, which are all in the current scope and have values 1, 2, and 3 respectively. Therefore, the value of d is 1 2 3.
In block d, another variable e is declared and assigned the concatenation of variables a, b, and c, which are still in the current scope and have the same values. Hence, the value of e is also 1 2 3.
In summary, the value of variable c in block d is 2, not 3.
To learn more about concatenation click here : brainly.com/question/3109469
#SPJ11
when the angle of an incline with a block resting on it increases the normal support force? A) decreases B) increases C) stays the same
Answers
Answer:
normal force decreases
Step-by-step explanation:
N=mgcosθ, and cosine decreases as theta increases
consider joining our disc*rd server for unlimited hw help! we also have an active giveaway rn. code: RPEdT3erFm <3
Answer:
A) decreases
Step-by-step explanation:
As the angle of the incline increases, the normal force decreases, which decreases the frictional force. The incline can be raised until the object just begins to slide.
(1 point) using: limx→3f(x)=1 and limx→3g(x)=8, evaluate the limits,
Answers
The limit of the function f(x) as x approaches 3 is 1, and the limit of the function g(x) as x approaches 3 is 8.
Given that \(\(\lim_{{x \to 3}} f(x) = 1\)\) and \(\(\lim_{{x \to 3}} g(x) = 8\)\), we can evaluate the limits as follows:
\(\[\lim_{{x \to 3}} (f(x) + g(x)) = \lim_{{x \to 3}} f(x) + \lim_{{x \to 3}} g(x) = 1 + 8 = 9.\]\)
This is known as the limit addition property, which states that the limit of the sum of two functions is equal to the sum of their individual limits if both limits exist.
Similarly, we can evaluate the limit of the product of f(x) and g(x):
\(\[\lim_{{x \to 3}} (f(x) \cdot g(x)) = \lim_{{x \to 3}} f(x) \cdot \lim_{{x \to 3}} g(x) = 1 \cdot 8 = 8.\]\)
This is known as the limit multiplication property, which states that the limit of the product of two functions is equal to the product of their individual limits if both limits exist.
In conclusion, the limit of the sum of f(x) and g(x) as x approaches 3 is 9, and the limit of the product of f(x) and g(x) as x approaches 3 is 8.
To learn more about function refer:
https://brainly.com/question/25638609
#SPJ11
Each pair of polygons is similar. Find the value of x.

Answers
The value of x for the similar triangles is equal to 13.
How to calculate for x for the similar trianglesWe have the triangles to be similar, this implies that the length 8 of the smaller triangle is similar to the length x - 1 of the larger triangle
and the length 10 of the smaller triangle is similar to the length x + 2 of the larger triangle
so;
10/(x + 2) = 8/(x - 1)
10(x - 1) = 8(x + 2) {cross multiplication}
10x - 10 = 8x + 16
10x - 8x = 16 + 10 {collect like terms}
2x = 26
x = 26/6 {divide through by 6}
x = 13.
Therefore, the value of x for the similar triangles is equal to 13.
Know more about similar triangles here:https://brainly.com/question/14285697
#SPJ1
A trampoline park has a trampoline that is 8 yards wide and 12 yards long. Approximate the distance (in yards) between opposite con
nearest tenth.

Answers
The distance between the opposite sides of the trampoline can be found to be 14. 42 yards
How to find the distance ?To find the distance between the opposite sides of the trampoline, we are essentially finding the diagonal length. We can use the Pythagorean theorem to do this by dividing the trampoline into two right triangles.
The distance between the opposite sides would then be:
c ² = a ² + b ²
c ² = 8 ² + 12 ²
c ² = 64 + 144
c ² = 208
c = √ 208
c = 14. 42 yards
Find out more on distance at https://brainly.com/question/29300978
#SPJ1
Anybody know number 11

Answers
Answer:
27
Step-by-step explanation:
i think
Step-by-step explanation:
\(your \: answer \: is \: option \: c \\ 11\)

help me with this question please

Answers
Answer:
N+1
Step-by-step explanation:
It begins with = 2
then n+1=3
then n+2=4 and so on it is n+1
What happens if the slope is undefined? Provide an example of two points that would be on a line with an undefined slope.
Answers
What happens when the slope of a line is undefined is that, the line is a vertical line that crosses the x-axis.
The points could be (1, 5) and (1, 10)
How to explain the undefined slope?It is known that linear equations have slopes
These slopes are the average rate of change of the function
The values of these slopes can be
ZeroPositive or negativeUndefinedWhen the slope is undefined, it means that the line is a vertical line
An example of the vertices on such line is (x, y) and (x, y + n)
See that the x coordinate remains constant, while the y coordinate changed
Take for instance, a line that passes through (1, 5) and (1, 10) would have an undefined slope
Read more about slopes at
https://brainly.com/question/11322966
#SPJ1
phân tích đa thức x^3 - x thành phân tử
Answers
Answer:
1
Step-by-step explanation:
What is the solution to the equation x\6 = 4\12?options:x = 2x = 6x = 4x = 1
Answers
SOLUTION
We want to solve the equation
\(\frac{x}{6}=\frac{4}{12}\)cross multiplying, we have
\(\begin{gathered} 12\times x=6\times4 \\ 12x=24 \\ x=\frac{24}{12} \\ x=2 \end{gathered}\)Hence the answer is x = 2, the first option
Which of the following correctly isolates the constant for the polynomial: x2 – 12x + 27
A. x^2 – 12x = 27
B. x^2 - 12x = 36
C. x^2 - 12x = -27
D. x^2 + 27 = 12x

Answers
Answer:
x^2 - 12x = -27
Step-by-step explanation:
Here, we want to isolate the constant for the polynomial
To do this, we start by setting the expression to zero
Afterwards, we can bring the constant term over the equal to sign, giving a change in sign value
Mathematically, we have this as;
x^2 - 12x + 27 = 0
x^2 - 12x = -27
In triangle PQR if angle P- angle Q=42° and angle Q - angle R=21°, find angle P ,angle Q and angle R .
Answers
Answer:
P = 95°Q = 53°R = 32°Step-by-step explanation:
In ∆PQR, you have the angle relations P-Q = 42 and Q-R = 21. You want the measures of all the angles.
Angle sumThe sum of the angles in the triangle is 180°. Using the given relation between P and Q, we have ...
P = Q +42
Using the given relation between Q and R, we have ...
R = Q -21
Then the angle sum is ...
P +Q +R = 180
(Q +42) +Q +(Q -21) = 180 . . . . . . substitute for P and R
3Q +21 = 180 . . . . . . . . . . . . . collect terms
Q +7 = 60 . . . . . . . . . . . . divide by 3
Q = 53 . . . . . . . . . . . subtract 7
P = Q +42 = 95
R = Q -21 = 32
The angles P, Q, R are 95°, 53°, and 32°, respectively.
\(\bold{\huge{\underline{ Solution }}}\)
Given :- We have triangle PQR \(\angle{P - {\angle}Q = 42{\degree}}\) \(\angle{Q - {\angle} R = 21{\degree}}\) To Find :- We have to find the value of angle P , angle Q and angle R Let's Solve :-According to the question,
\(\sf{\angle{P - {\angle}Q = 42{\degree}}}\)
\(\sf{\angle{P = 42{\degree} + {\angle}Q ...eq(i) }}\)
\(\sf{\angle{Q - {\angle} R = 21{\degree} }}\)
\(\sf{\angle{Q - 21{\degree} = {\angle}R}}\)
\(\sf{\angle{R = {\angle}Q - 21{\degree}...eq(ii) }}\)
We know that,
The sum of the angles of triangle equal to 180°Therefore ,
By using angle sum property :-
\(\sf{{\angle} P + {\angle}Q + {\angle} R = 180 {\degree}}\)
From eq(i) in eq(ii) :-
\(\sf{42 {\degree} + {\angle} Q + {\angle} Q + {\angle} Q - 21 {\degree}= 180 {\degree}}\)
\(\sf{ {\angle} 3Q + 21 {\degree}= 180 {\degree}}\)
\(\sf{ {\angle} 3Q = 180 {\degree} - 21{\degree}}\)
\(\sf{ {\angle} 3Q = 159 {\degree}}\)
\(\sf{ {\angle} Q = {\dfrac{159}{3}}}\)
\(\sf{ {\angle} Q = 53{\degree}}\)
Thus , The value of Q is 53° .
Substitute the value of Q in eq(i) :-
\(\sf{\angle{P = 42{\degree} + 53{\degree} }}\)
\(\sf{ {\angle} P = 95 {\degree}}\)
Now , For value of R --- substitute the value of Q in eq(ii) :-
\(\sf{\angle{R = 53 {\degree} - 21{\degree} }}\)
\(\sf{ {\angle} P = 32 {\degree}}\)
Hence , The values of angle P, angle Q and angle R are 95° , 53° and 32°.
a) a research article described a simple random sample of 584 smokers who tried to quit smoking by using either a nicotine patch or e-cigarettes, fake cigarettes producing nicotine in water vapor form. after six months, 7.3% of those using e-cigarettes had stopped smoking, compared with 5.8% of those wearing the patch. to see if quitting result is significantly associated with the method used, which statistical inference procedure should we use? matched
Answers
To see if quitting result is significantly associated with the method used, which statistical inference procedure which should be used is the Chi-square test for two-way table.
A random sample of 584 smokers who attempted to quit smoking and were observed using the method they used to help themselves to achieve their goal was taken in order to determine whether there is a correlation between the percentage of people who successfully stop smoking and the method they used to do so (nicotine-patch or e-cigarettes). The percentage of subjects who successfully quit smoking after six months.
The t-test is not appropriate in this situation because the population mean is being tested by this statistic.
The percentage of participants who successfully quit smoking using either technique is the study's dependent variable.
The variable must be categorizable in order to do Chi-Square tests, and since the data can be arranged in a 2x2 table, all anticipated frequencies must be greater than 5.
The Goodness-to-Fit test seeks to determine if a population adheres to a particular theoretical model.
In this case, it's important to compare the percentage of smokers who were able to successfully stop using both methods and the percentage who were unsuccessful.
To learn more about Chi-Square tests
https://brainly.com/question/14082240
#SPJ4
Calculate the circumference

Answers
Answer:
30
Step-by-step explanation:
you times 20 by 11 so that
I need help with this problem please

Answers
Answer:
x=5
Step-by-step explanation:
The midsegment of a trapezoid is equal to the sum of the two bases divided by two. This means that 17 = (2x + 1 + 3x + 8)/2. To start, multiply both sides by 2 to get 34 = 2x + 1 + 3x + 8. Next, combine like terms to get 34 = 5x + 9. Subtract 9 from both sides for 25 = 5x. Finally, divide both sides by 5 to get an x-value of 5.
Callie grows lilies to sell at a local gift shop and market. She notices that she sells 30 fewer white lilies and 20 more yellow lilies per day at the gift
shop than she does at the market. Callie uses this pattern to predict the number of white and yellow lilies she will sell at the market.
Let w represent the number of white lilies Callie sells per day at the gift shop.
Let y represent the number of yellow lilies Callie sells per day at the gift shop.
Create expressions that Callie can use to predict the number of white and yellow lilies she will sell at the market. Move variables and numbers
to the lines to create each expression.
Number of white lilies Callie will sell at the market:
Number of yellow lilies Callie will sell at the market:
Answers
The expressions that Callie can use to predict the number of white and yellow lilies she will sell at the market are:
Number of white lilies Callie will sell at the market: w - 30Number of yellow lilies Callie will sell at the market: y + 20How to Calculate Callie's Sales?If w represents the number of white lilies Callie sells per day at the gift shop, then the number of white lilies she will sell at the market will be w - 30 (30 fewer).
Similarly, if y represents the number of yellow lilies Callie sells per day at the gift shop, then the number of yellow lilies she will sell at the market will be y + 20 (20 more).
Therefore, the expressions that Callie can use to predict the number of white and yellow lilies she will sell at the market are:
Number of white lilies Callie will sell at the market: w - 30
Number of yellow lilies Callie will sell at the market: y + 20
Learn more about sales here: https://brainly.com/question/24951536
#SPJ1
Amanda exercised for 10 minutes every day in the first week, 20 minutes in the second week, 30 minutes in the third week, and 40 minutes in the fourth week.
Billy exercised for 5 minutes every day in the first week, 10 minutes in the second week, 20 minutes in the third week, and 40 minutes in the fourth week.
Which statement best describes the methods used by Amanda and Billy to increase the time they spent exercising? (1 point)
Group of answer choices
Amanda's method is linear because the number of minutes increased by an equal number every week.
Billy's method is linear because the number of minutes increased by an equal factor every week.
Both Billy's and Amanda's methods are exponential because the number of minutes increased by an equal factor every week.
Both Billy's and Amanda's methods are exponential because the number of minutes increased by an equal number every week.
Answers
Amanda's method is linear because the number of minutes increased by an equal number every week.
Determine whether or not the distribution is a discrete probability distribution and select the reason why or why not.
x −1 3 5
P(X=x)P(X=x) 0.05 0.38 0.57
Answer
2 Points
Keypad
Tables
First, decide whether the distribution is a discrete probability distribution, then select the reason for making this decision.
Answers
The distribution is a discrete probability distribution because the sum equals 1.
To determine whether or not the distribution is a discrete probability distribution, we need to check if the probabilities sum up to 1 and if all the probabilities are non-negative for every possible value of X. Also, the values of X must be countable.
Here, the given table represents the probability distribution of a discrete random variable X. Therefore, it is a discrete probability distribution.
The sum of probabilities is:
P(X = −1) + P(X = 3) + P(X = 5) = 0.05 + 0.38 + 0.57 = 1
and all the probabilities are non-negative.
Therefore, the distribution is a discrete probability distribution.
For more such questions on Discrete probability distribution.
https://brainly.com/question/31197941#
#SPJ11
Statistics prove that dissatisfied customers are dangerous for a salesperson. When they are not happy with the product or service sold, they will tell ____ other people about it:
Answers
Dissatisfied customers are likely to share their negative experiences with an average of 9-15 people, but with the reach of social media, their impact can be significantly amplified, potentially influencing a wider audience and damaging a salesperson's reputation and sales.
When dissatisfied with a product or service, customers are more likely to share their negative experiences with others. The exact number of people they may tell can vary, but it's often cited that dissatisfied customers will share their negative experiences with an average of 9 to 15 other people.
This number can increase significantly in the age of social media, where dissatisfied customers have the ability to reach a much larger audience through online platforms and reviews. Therefore, it's crucial for salespeople to address customer concerns and ensure customer satisfaction to prevent negative word-of-mouth and potential damage to their reputation.
To learn more about average Click Here: brainly.com/question/8501033
#SPJ11
Question 1 (2 x 12 = 24 marks) Analyze and discuss the performance (in Big-O notation) of implementing the following methods over Singly Linked List and Doubly Linked List Data structures: To be submitted through Turnitin.Maximum allowed similaritv is 15% Operation Singly Linked List Doubly Linked List add to start of list Big-O notation Explanation add to end of list Big-O notation Explanation add at given index Big-O notation Explanation
Answers
In analyzing the performance of implementing the given methods over Singly Linked List and Doubly Linked List data structures, we consider the Big-O notation, which provides insight into the time complexity of these operations as the size of the list increases.
Add to Start of List:
Singly Linked List: O(1)
Doubly Linked List: O(1)
Both Singly Linked List and Doubly Linked List offer constant time complexity, O(1), for adding an element to the start of the list.
This is because the operation only involves updating the head pointer (for the Singly Linked List) or the head and previous pointers (for the Doubly Linked List). It does not require traversing the entire list, regardless of its size.
Add to End of List:
Singly Linked List: O(n)
Doubly Linked List: O(1)
Adding an element to the end of a Singly Linked List has a time complexity of O(n), where n is the number of elements in the list. This is because we need to traverse the entire list to reach the end before adding the new element.
In contrast, a Doubly Linked List offers a constant time complexity of O(1) for adding an element to the end.
This is possible because the list maintains a reference to both the tail and the previous node, allowing efficient insertion.
Add at Given Index:
Singly Linked List: O(n)
Doubly Linked List: O(n)
Adding an element at a given index in both Singly Linked List and Doubly Linked List has a time complexity of O(n), where n is the number of elements in the list.
This is because, in both cases, we need to traverse the list to the desired index, which takes linear time.
Additionally, for a Doubly Linked List, we need to update the previous and next pointers of the surrounding nodes to accommodate the new element.
In summary, Singly Linked List has a constant time complexity of O(1) for adding to the start and a linear time complexity of O(n) for adding to the end or at a given index.
On the other hand, Doubly Linked List offers constant time complexity of O(1) for adding to both the start and the end, but still requires linear time complexity of O(n) for adding at a given index due to the need for traversal.
To learn more about Big-O notation visit:
brainly.com/question/30452896
#SPJ11
HELP HELP HELP ILL MARK YOU BRAINLIEST

Answers
The answer would be 128z^9.
This is because when you multiply exponents with a variable (z), you keep the base the same (8z and 16z), but you add the exponents together.
I need help with this math ASAP due today

Answers
Answer:
C. 1/16 choice c because this is what the calculator gave me
Given f(x)=7x 2
+4x find a value z where the average rate of change between 2 and 4 is equal to the instantaneous rate of change of f(x) at 2 . W When entering values make sure any decimal is represented by a point and not a comma. for eg 2.4 not 2,4]
Answers
The value z where the average rate of change between 2 and 4 is equal to the instantaneous rate of change of f(x) at 2 is z = 2.
To find a value z where the average rate of change between 2 and 4 is equal to the instantaneous rate of change of f(x) at 2, we need to compare the average rate of change and the derivative of the function.
The average rate of change between 2 and 4 is given by:
Average rate of change = (f(4) - f(2)) / (4 - 2)
Plugging in the function f(x) = \(7x^2 + 4x\)
Average rate of change = \((7(4)^2 + 4(4) - (7(2)^2 + 4(2))) / (4 - 2) = (112 + 16 - 56 - 8) / 2 = 64 / 2 = 32\)
The instantaneous rate of change of f(x) at 2 is given by the derivative of f(x) evaluated at x = 2:
\(f'(x) = d/dx (7x^2 + 4x) = 14x + 4\)
Instantaneous rate of change at x = 2:
f'(2) = 14(2) + 4 = 28 + 4 = 32
To find a value z where the average rate of change equals the instantaneous rate of change, we need to find a value z where:
Average rate of change = Instantaneous rate of change
32 = 14z + 4
Solving for z, we have:
14z + 4 = 32
14z = 28
z = 28 / 14
z = 2
Therefore, the value z where the average rate of change between 2 and 4 is equal to the instantaneous rate of change of f(x) at 2 is z = 2.
To know more about average rate refer here:
https://brainly.com/question/28739131
#SPJ11