Solve the right triangle. 5
6
F
E
D
30°
Write your answers in simplified, rationalized form. Do not round. DF =
DE =
10
m∠D =
60
°
Answers
The length of the other leg is 8 cm, and the measures of the two acute angles are approximately 36.87° and 53.13°.
To solve the right triangle, we can use the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Therefore, we have:
\(10^2 = 6^2 + x^2 \\x = sqrt(10^2 - 6^2) = 8 cm\)
So the length of the other leg is 8 cm.
Let θ be one of the acute angles:
sin(θ) = opposite/hypotenuse = 6/10 = 0.6
cos(θ) = adjacent/hypotenuse = x/10 = 8/10 = 0.8
θ ≈ 36.87°.
Since the other acute angle is complementary to θ, its measure is 90° - 36.87° = 53.13°.
To know more about Pythagorean theorem, here
brainly.com/question/14930619
#SPJ4
--The complete Question is, A right triangle has a hypotenuse of length 10 cm and one leg of length 6 cm. Solve the right triangle, finding the length of the other leg and the measures of the two acute angles. --
Related Questions
In men’s tennis, a match consists of 5 sets, with 3 sets required to win a match. Ivan
and Roger play a match, and suppose the probability that Ivan wins a set is p. Let
P (s) be the probability that set s is the set in which the match is decided. Thus s
can be 1, 2, 3, 4 or 5.
(a) Find expressions for P (s), s = 1, 2, 3, 4, 5 in terms of p.
(b) Let S be the random variable representing the set that decides the match. Find
E(S) in terms of p. (Optional: find Var(X) in terms of p).
Answers
P(1) = p³,S = 1 P(2) = 3p²(1 − p),S = 2 P(3) = 3p(1 − p)²,S = 3 P(4) = (1 − p)³p,S = 4 P(5) = 3(1 − p)²p,S = 5 E(S) = 4 − 3p Var(S) = 30p(1 − p)(1 − 2p)
(a)P(s) is the probability that set s is the deciding set, and it can be expressed as follows:
• P(1) = p³ : Ivan wins the first 3 sets.
• P(2) = 3p²(1 − p) : Ivan wins two of the first three sets and the match is decided in the fourth set.
• P(3) = 3p(1 − p)² : Ivan wins two of the first three sets and the match is decided in the fifth set.
• P(4) = (1 − p)³p : Roger wins the first 3 sets.
• P(5) = 3(1 − p)²p : Roger wins two of the first three sets and the match is decided in the fourth set. (Note that P(4) and P(5) are equal.)
(b)Let S be a random variable that represents the set that decides the match. We can see that:
• S = 1 with probability P(1) = p³
• S = 2 with probability P(2) = 3p²(1 − p)
• S = 3 with probability P(3) = 3p(1 − p)²
• S = 4 with probability P(4) = (1 − p)³p
• S = 5 with probability P(5) = 3(1 − p)²p
The expected value of S, which is E(S), is given by:
E(S) = 1 x P(1) + 2 x P(2) + 3 x P(3) + 4 x P(4) + 5 x P(5)
E(S) = p³ + 6p²(1 − p) + 9p(1 − p)² + 4(1 − p)³p + 15(1 − p)²p
E(S) = 4 − 3p
This is the expected value of the set that decides the match, expressed in terms of p.
Optional: Find Var(S), which is the variance of the set that decides the match.
Var(S) = E(S²) − [E(S)]² We can see that:
S² = 1² x P(1) + 2² x P(2) + 3² x P(3) + 4² x P(4) + 5² x P(5)S² = p³ + 12p²(1 − p) + 27p(1 − p)² + 16(1 − p)³p + 75(1 − p)²p Thus, Var(S) = p³ + 12p²(1 − p) + 27p(1 − p)² + 16(1 − p)³p + 75(1 − p)²p − (4 − 3p)²
Var(S) = 30p(1 − p)(1 − 2p)
This is the variance of the set that decides the match, expressed in terms of p.
For more random variable question, refer to:
https://brainly.com/question/30789758
#SPJ11
Gavin deposited $200 into his savings account that is compounded semi-annually at an interest rate of 9%. Gavin hoped he would have enough money in 8 years to buy a $400 gaming console for college. Is Gavin correct? Write and solve an equation, showing your work to justify your answer
Answers
Answer:
His answer was correct:
(200*0.09)=18
18*16=288
200+288=488
which expression is equivalent to 34 divided by 4
Answers
Answer:
32/4 = 8 \(\frac{1}{2}\) = 8.5
Step-by-step explanation:
34/4 = 8 \(\frac{2}{4}\)
8 \(\frac{2}{4}\) = 8 \(\frac{1}{2}\) = 8.5
Answer:
Below
Step-by-step explanation:
34 ÷ 4 = 34/ 4 = 8 2/4 = 8 1/2 <===pick the one you need
work out the volume of a frustum please help me i’ll give u brainleist

Answers
Answer: 137.25π ≈ 431.18 cm³
Step-by-step explanation:
Entire Cone - Tip of Cone = Frustrum
\(V_{cone}=\dfrac{1}{3}\pi r^2h\\\\\\V_{Entire}=\dfrac{1}{3}\pi (6)^2(12)\quad =\quad 144\pi\\\\V_{Tip}=\dfrac{1}{3}\pi \bigg(\dfrac{6}{4}\bigg)^2\bigg(\dfrac{12}{4}\bigg)\quad =\quad \dfrac{27}{4}\pi\\\\\\\\V_{Frustrum}=V_{Entire}-V_{Tip}\\\\.\qquad \qquad =144\pi-\dfrac{27}{4}\pi\\\\.\qquad \qquad =\dfrac{549}{4}\pi\\\\.\qquad \qquad =137.25\pi\\\\.\qquad \qquad=\large\boxed{431.18}\)
Answer: 137.25π ≈ 431.18 cm³
Step-by-step explanation:
Entire Cone - Tip of Cone = Frustrum
the sample mean is 59.1 km with a sample standard deviation of 2.31 km. assume the population is normally distributed. the p-value for the test is:
Answers
The p-value for the test is found as 0.05 for the given hypothesis.
Given,Sample mean = 59.1 km
Sample standard deviation = 2.31 km
Population is normally distributed
P-value for the test is to be determined.
To find the p-value, we need to perform a hypothesis test. Here, we have to test whether the null hypothesis is true or not.
Hypothesis statements:
Null hypothesis (H0): µ = 60 km (The population mean is 60 km)
Alternative hypothesis (Ha): µ ≠ 60 km (The population mean is not equal to 60 km)
Level of significance, α = 0.05
Z-score formula is given as,Z = (x - µ) / (σ/√n)
Where,x = Sample mean = 59.1 km
µ = Population mean
σ = Standard deviation of the population = 2.31 km
n = Sample size
We have,σ/√n = 2.31/√n
For α = 0.05, the two-tailed critical values are ±1.96
Now, the calculated Z-score is given as,
Z = (59.1 - 60) / (2.31/√n)
Z = - (0.9) * ( √n / 2.31)
P(Z < -1.96) = 0.025 and P(Z > 1.96) = 0.025
P-value = P(Z < -1.96) + P(Z > 1.96)
P-value = 0.025 + 0.025
P-value = 0.05
Know more about the p-value
https://brainly.com/question/13786078
#SPJ11
Consider the PDE au(x, t) = 4 d²u(x, t) 2 Ət əx² For each of BCs and ICs, solve the initial value problem. du(π,t) a) BCs: u(0,t)=0 = = 0 and əx IC: u(x,0) = x ANSWER: f(x)= n=1 u(2,t) = 0 and u(0,t)=0 u(x,0)=sin x ANSWER: f(x)=¹1_sin(2 + nx) na n=1 1+ 2 X b) BCs: IC: 8 (2n-1) T n+1 (-1)041 -4(2n-1)²t sin(2-nπ) nπ 1- 2 e sin (2n-1) 2 na sin X 2 -(nn)²t x -X
Answers
the solution for the initial value problem is: u(x, t) = sin(sqrt(-λ² * (a / 4)) * x) * exp(-λ² * t) where λ = ± sqrt(-4n² / a), and n is a non-zero integer.
The given partial differential equation is:
au(x, t) = 4 * (d²u(x, t) / dt²) / (dx²)
a) BCs (Boundary Conditions):
We have u(0, t) = 0 and u(π, t) = 0.
IC (Initial Condition):
We have u(x, 0) = x.
To solve this initial value problem, we need to find a function f(x) that satisfies the given boundary conditions and initial condition.
The solution for f(x) can be found using the method of separation of variables. Assuming u(x, t) = X(x) * T(t), we can rewrite the equation as:
X(x) * T'(t) = 4 * X''(x) * T(t) / a
Dividing both sides by X(x) * T(t) gives:
T'(t) / T(t) = 4 * X''(x) / (a * X(x))
Since the left side only depends on t and the right side only depends on x, both sides must be equal to a constant value, which we'll call -λ².
T'(t) / T(t) = -λ²
X''(x) / X(x) = -λ² * (a / 4)
Solving the first equation gives T(t) = C1 * exp(-λ² * t), where C1 is a constant.
Solving the second equation gives X(x) = C2 * sin(sqrt(-λ² * (a / 4)) * x) + C3 * cos(sqrt(-λ² * (a / 4)) * x), where C2 and C3 are constants.
Now, applying the boundary conditions:
1) u(0, t) = 0:
Plugging in x = 0 into the solution X(x) gives C3 * cos(0) = 0, which implies C3 = 0.
2) u(π, t) = 0:
Plugging in x = π into the solution X(x) gives C2 * sin(sqrt(-λ² * (a / 4)) * π) = 0. To satisfy this condition, we need the sine term to be zero, which means sqrt(-λ² * (a / 4)) * π = n * π, where n is an integer. Solving for λ, we get λ = ± sqrt(-4n² / a), where n is a non-zero integer.
Now, let's find the expression for u(x, t) using the initial condition:
u(x, 0) = X(x) * T(0) = x
Plugging in t = 0 and X(x) = C2 * sin(sqrt(-λ² * (a / 4)) * x) into the equation above, we get:
C2 * sin(sqrt(-λ² * (a / 4)) * x) * C1 = x
This implies C2 * C1 = 1, so we can choose C1 = 1 and C2 = 1.
Therefore, the solution for the initial value problem is:
u(x, t) = sin(sqrt(-λ² * (a / 4)) * x) * exp(-λ² * t)
where λ = ± sqrt(-4n² / a), and n is a non-zero integer.
Note: Please double-check the provided equation and ensure the values of a and the given boundary conditions are correctly represented in the equation.
To know more about Equation related question visit:
https://brainly.com/question/29657983
#SPJ11
Find the value of the unknown in the figure below

Answers
b =(17,6x 8,9):19,7=7,95
a line passes through both points (-2, 2) and (8, 9). what is the angle between the line and the x axis?
Answers
Step-by-step explanation:
To find the angle between a line and the x-axis, we need to calculate the slope of the line first. The slope of a line passing through two points (x₁, y₁) and (x₂, y₂) is given by the formula:
m = (y₂ - y₁) / (x₂ - x₁)
Using the points (-2, 2) and (8, 9), we can substitute the values into the formula:
m = (9 - 2) / (8 - (-2))
= 7 / 10
= 0.7
The slope of the line is 0.7. The angle between the line and the x-axis can be found using the inverse tangent (arctan) function. The tangent of an angle is equal to the slope of the line, so we can write:
tan(θ) = 0.7
Taking the inverse tangent of both sides, we find:
θ = arctan(0.7)
Using a calculator, we can evaluate this to be approximately:
θ ≈ 35.87 degrees
Therefore, the angle between the line and the x-axis is approximately 35.87 degrees.
A bag contains black and white tokens in a ratio of 3:2.
8 black tickets and 2 white tokens are added to the bag.
The ratio of black to white tokens are now 2:1.
How many white tokens were in the bag to begin with?
Answers
The initial number of white tokens in the bag is given as follows:
8.
How to obtain the amount?The amount is obtained by a system of equations, for which the variables are given as follows:
Variable x: number of black tokens.Variable y: number of white tokens.A bag contains black and white tokens in a ratio of 3:2, hence:
x/y = 3/2.
2x = 3y
x = 1.5y.
8 black tickets and 2 white tokens are added to the bag. The ratio of black to white tokens are now 2:1, hence:
(x + 8)/(y + 2) = 2.
Replacing the first equation into the second, the initial amount of white tokens is given as follows:
(1.5y + 8)/(y + 2) = 2
2(y + 2) = 1.5y + 8
2y + 4 = 1.5y + 8
0.5y = 4
y = 8.
More can be learned about a system of equations at https://brainly.com/question/30374328
#SPJ1
round to ten-thousandth (cut off says quadrant 1, I couldnt fit it all in.)

Answers
sin(A)=2/5
trig identity:
* sin^2(A)+cos^2(A)=1
* tan(A)=sin(A)/cos(A)
find: tan(A)
\(\begin{gathered} \sin ^2(A)+\cos ^2(A)=1 \\ (\frac{2}{5})^2+\cos ^2(A)=1 \\ \cos ^2(A)=1-\frac{4}{25} \\ \cos ^2(A)=\frac{21}{25} \\ \cos (A)=\sqrt[]{\frac{21}{25}}=\frac{\sqrt[]{21}}{5} \end{gathered}\)\(\begin{gathered} \tan (A)=\frac{\sin (A)}{\cos (A)} \\ \tan (A)=\frac{\frac{2}{5}}{\frac{\sqrt[]{21}}{5}} \\ \tan (A)=\frac{2}{\sqrt[]{21}}\approx0.436 \end{gathered}\)Hi! If you could please do my assignment, I'd be grateful! I'll also mark brainliest, giving thanks, and hearts for the best. Thank you and have a great day!

Answers
Answer:
Smaller Trapezoid: 12
Bigger Paralleogram: 24
Bigger Triangle: 22/40
Smaller Triangle : 2.75/ 5
Step-by-step explanation:
cross multiplication
Bigger Paralleogram: 9 x 16= 144 / 6= 24
Bigger Triangle: 5 x 22= 110 / 2.75 = 40
hope this helps
question 9
9. Given ABCD
EFGH, find the length of GH.
A. 8
B. 7
C. 5
D. 10
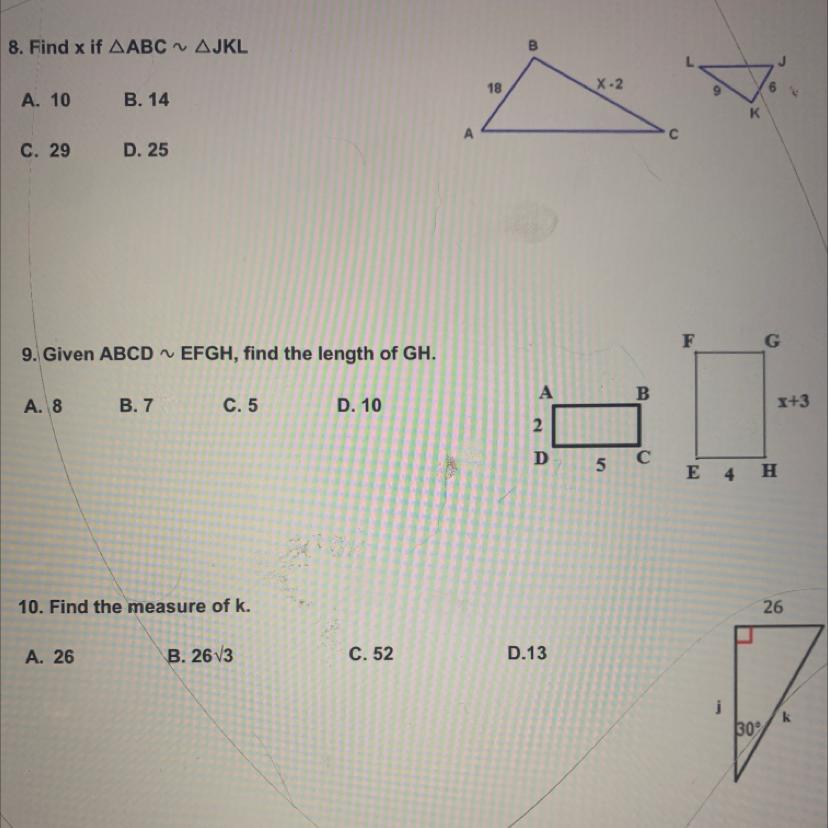
Answers
The step-step explanation:
Hurry! *50 point's and brainly to the one who solve this!!* Please and thank you!
2 .) What is the special angle pair relationship between < 8 and < 4?
3.) What is the special pair relationship < 2 and < 3?
4, using the figure below, Maggie used the definition of vertical angles to help her solve for x. Since vertical angles are congruent, she set the two given expressions equal other. After solving for x, her teacher said she got the wrong value for x. Exaple where Maggie made her mistake when solving for x.


Answers
Answer:
Step-by-step explanation:
2) What type of angle is 4 and 8?
I What is the special angle pair relationship between < 8 and < 4?
Angle 4 and angle 8 are also alternate interior angles. Alternate exterior angles: Pairs of exterior angles on opposite sides of the transversal. Angle 2 and angle 7 are alternate exterior angles.
3)Twos are generally thoughtful, people-oriented, and caring, while Threes are resourceful, energetic, and determined.
4) Do not use a protractor. Use the properties of straight and vertical angles to help you.
Kari can't wait to read the newest issue of her favorite comic, The Notorious Ninja, so she plans to bike 3 miles to the comic book store after school. If Kari can usually bike 12 miles in an hour, how many minutes will it take her to get there?
Answers
The minutes it would take Kari to get to the comic store is 15 minutes.
How many minutes would it take to get to the comic store?The average speed is the total distance per time. It is determined by dividing the total distance travelled by the total time travelled.
Average speed = total distance / total time
Kari's average speed is 12 miles per hour.
In order to determine the time it would take Kari to the comic store, divide the total distance by the average speed.
Division is the process used to determine the quotient of two or more numbers. Division entails grouping a number into equal groups using another number. The sign used to denote division is ÷
Time = total distance / average speed
3 /12 = 1/4 hour
1/4 x 60 = 15 minutes
To learn more about average speed, please check: https://brainly.com/question/21734785
#SPJ1
Amanda is 52 inches tall. Barry is 19 inches taller than Amanda. How
many inches tall is Barry?
Use the base-ten blocks. Click the Base-Ten Blocks button below.
Answers
Answer:
Barry is 71 inches tall
Step-by-step explanation:
52 + 19 = 71
Plzzzzzzzzz i need help

Answers
Answer:
Area = base x height
Step-by-step explanation:
8X11=88sq
Answer:
88 units^2
Step-by-step explanation:
The area of a parallelogram can be found using he following formula:
a=b*h
where b is the base and h is the height.
We know that 11 units is the base and 8 units is the height (forms a right angle with one of the bases).
b= 11 units
h= 8 units
Substitute these values into the formula.
a= 11 units * 8 units
Multiply
a= 88 units^2
The area of the parallelogram is 88 square units.
Hugh bought some magizines that cost 3.95 each and some books that cost 8.95 each. He spent a total of 47.65.If Hugh bought 3 magazines,how many books did he buy
Answers
Answer:
4 books
Step-by-step explanation:
We are told that: Hugh bought some magazines that cost 3.95 each
Hugh bought 3 magazines.
Hence, total cost of magazines = 3 magazines × 3.95
= 11.85.
Total cost of magazines = 11.85
From the question, we know that, the total amount Hugh spent = 47.65
Hence, The total cost for books =
Total amount spent - Total cost of magazines
= 47.65 - 11.85
= 35.80
Therefore, the total cost of books = 35.80
We are told in the question that the cost of books is 8.95 each or 8.95 per book.
Hence, the number of books that Hugh bought is calculated as :
35.80/8.95
= 4 books
Therefore, Hugh bought 4 books
solve for x in [0, π]: 2 cos(x) > sec(x)
Answers
The value for x is 7π/6 and 11π/6.
sin2xsecx+2cosx=0
(2sinxcosx)(1/cosx)+2cosx=0
sinxcosx/cosx+2cosx=0
So,
2sinx+2cosx=0
2(sinx+cosx)=0
(2(sinx+cosx))²=0
4(sin²x+cos²x+2sinxcosx)=0
hence,
(sin²x+cos²x+2sinxcosx)/4=0/4
sin2x+cos2x+2sinxcosx=0
1+sin2x=0
sinx=−1/2
=7π/6 and 11π/6
Know more about trigonometry at:
https://brainly.com/question/20519838
#SPJ4
If the r = + 0.8, we would say: As X scores increase, the Y scores increase; and
the magnitude is strong. Explain what each of the following correlation coefficients indicates about the
direction and magnitude in which Y scores change as X scores increase.
a. -1.0
b. +0.32
c. -0.10
d. -0.71
Answers
If the correlation coefficient r is -1.0, it means that there is a perfect negative linear relationship between X and Y.
a) As X scores increase, Y scores decrease in a perfectly consistent manner. The magnitude is strong.
b) If the correlation coefficient r is +0.32, it means that there is a positive linear relationship between X and Y, but it is a weak relationship. As X scores increase, Y scores tend to increase, but not in a perfectly consistent manner. The magnitude is weak.
c) If the correlation coefficient r is -0.10, it means that there is a weak negative linear relationship between X and Y. As X scores increase, Y scores tend to decrease, but not in a consistent manner. The magnitude is weak.
d) If the correlation coefficient r is -0.71, it means that there is a strong negative linear relationship between X and Y. As X scores increase, Y scores tend to decrease in a consistent manner. The magnitude is strong.
To learn more about correlation coefficient here:
https://brainly.com/question/27226153
#SPJ1
A charity run has prizes for the top finisher in each of 10 age categories. The
times of the prize-winners are shown. Which scatterplot accurately reflects
these data?
Age
12 16 20 25 33 37 43 50 61 71
Time (minutes) 23 19 16 15 19 20 24 25 26 33

Answers
Using it's concept, the scatter plot that accurately reflects the data given in the problem is scatter plot D.
What is a scatter plot?A scatter plot is a graph that maps each input in the data-set to it's respective output, as points.
Considering this concept, an age of 12(x - axis) should be mapped to a time in minutes of 23(y-axis), and so on, until an age of 71 is mapped to a time of 33 minutes, which happens in option D.
More can be learned about scatter plots at https://brainly.com/question/22968877
#SPJ1
Hi,please help and explain fully! How to Expand and Simplify brackets? I don't understand how to work out .

Answers
The fully expanded and simplified form of (x - 2)(2x + 4) is 2(x - 2)(x + 2).
Describe Rule for bracket simplification?Expanding a bracket means multiplying the terms inside the bracket by the term(s) outside the bracket. In the case of (x - 2)(2x + 4), we can use the FOIL method to expand the brackets:
F: Multiply the First terms in each bracket, which gives us x * 2x = 2x²
O: Multiply the Outer terms in each bracket, which gives us x * 4 = 4x
I: Multiply the Inner terms in each bracket, which gives us -2 * 2x = -4x
L: Multiply the Last terms in each bracket, which gives us -2 * 4 = -8
Putting these results together, we get:
(x - 2)(2x + 4) = 2x² + 4x - 4x - 8
Notice that the -4x and +4x terms cancel out, so we're left with:
(x - 2)(2x + 4) = 2x² - 8
So the expanded form of (x - 2)(2x + 4) is 2x² - 8.
To simplify this expression further, we can factor out a 2:
2x² - 8 = 2(x² - 4)
And then factor the quadratic expression inside the parentheses:
2(x² - 4) = 2(x - 2)(x + 2)
So the fully expanded and simplified form of (x - 2)(2x + 4) is 2(x - 2)(x + 2).
To know more about expression visit:
https://brainly.com/question/24242989
#SPJ1
This I my question any body help

Answers
Answer: table 2
Step-by-step explanation:
its because the rest of the tables do not have a pattern that ‘makes sense’ unlike table 2. for table 2, for every one 1 km there’s 10$
If the temperture is -4 an rises by 12 whats the new temperture
Answers
The new temperature would be 8 when the temperature is -4 and rises by 12.
Addition is a fundamental mathematical operation that is used to join two or more numbers or quantities. It entails calculating the sum of two or more values.
The sign "+" represents the procedure.
For example, adding 2 and 3 yields a total of 5, which is expressed as:
2 + 3 = 5
As per the question, If the temperature starts at -4 and rises by 12, we need to add 12 to the starting temperature to find the new temperature.
So, the new temperature would be:
-4 + 12 = 8
Therefore, the new temperature would be 8.
Learn more about Addition operations here:
brainly.com/question/25834626
#SPJ4
In the Second Law experiment, In the Second Law experiment, the acceleration is calculated by measuring the time for the cart to move from the start point to the end point and applying the kinematics equation: s= 1/2 at 2 Explain how this equation is used to find the acceleration.
Answers
The kinematics equation s = 1/2at² can be used to determine the acceleration in the Second Law Experiment, where acceleration is calculated by measuring the time taken for the cart to move from the start point to the end point.
Let's derive how the equation is used to find the acceleration from this experiment:
Drivation of kinematics equation:
The kinematics equation is derived by integrating the acceleration function twice with respect to time (t).
Acceleration, a = d²s/dt², where s is displacement, and d²s is the second derivative of displacement with respect to time.
taking integral w.r.t time twice:
∫ a dt = ∫ d²s/dt² dt integrating once gives, v = at + C₁ (where C₁ is a constant of integration)
integrating twice gives, s = 1/2at² + C₁t + C₂ (where C₂ is a constant of integration)
Thus, the kinematics equation for an object moving with constant acceleration can be represented by
s = 1/2at² + vit + s₀,
where s is the displacement, a is the acceleration, t is time, vi is initial velocity, and s₀ is initial displacement.
Know more about kinematics equation here
https://brainly.com/question/24458315
#SPJ11
1. What is the value of x? Show all of your work.
Answer:

Answers
Answer:
x=9
Step-by-step explanation:
pythagorean theorem
\(a^2+b^2=c^2\\a=6 \\b=x\\c=\sqrt{117} \\6^2+x^2=\sqrt{117} ^2\\36+x^2=117\\x^2=81\\\sqrt{x^2} =\sqrt{81} \\x=9\)
HELP IM GOING TO CRYY!!! Find the total area of the figure below. Round your answer to the nearest tenth.

Answers
Answer:
349.94
Step-by-step explanation:
First u add all the square sides because they all are the same which gives u 196 then u can see there is two half circles which if they add up will be a circle and the diameter is the same as the square sides then if the diameter is 14 then the radius will be 7 becaue 14/2 therefore u use the area of the circle which is
\(\pi \times {7}^{2} \)
then u add all the numbers.
explain each step to this question and show full working out to make sure the answer is correct: Amy, John, and Emily each earn the same monthly salary. Each month, Amy saves 20% of her salary and spends the rest of her salary. John spends 2/5 of his salary and saves the rest of his salary. The amount of salary Emily saves to the amount of salary she spends is 5:8. Workout who saves the most of their salary each month.
can you do this in 10 min or less, please
Answers
Answer:
To compare who saves the most of their salary each month among Amy, John, and Emily, we need to calculate the amount of salary each person saves.
Let's assume that the monthly salary of each person is 'S'. Then we can calculate the amount saved by each person as follows:
Amy:
Amount saved = 20% of S = 0.2S
Amount spent = S - 0.2S = 0.8S
John:
Amount spent = 2/5 of S = (2/5)S
Amount saved = S - (2/5)S = (3/5)S
Emily:
Let's assume that Emily saves '5x' and spends '8x' of her monthly salary.
Then, according to the question, we have:
Amount saved = 5x
Amount spent = 8x
We know that the ratio of the amount saved to the amount spent is 5:8, so we can write:
Amount saved / Amount spent = 5/8
Substituting the values of amount saved and amount spent, we get:
5x / 8x = 5/8
5x = (5/8) x 8x
5x = 5x
Therefore, the ratio of amount saved to amount spent is equal to 5:8. This means that Emily saves 5/13 of her monthly salary and spends 8/13 of her monthly salary.
So, the amount saved by each person is:
Amy: 0.2S
John: (3/5)S
Emily: 5/13 of S
Now, we need to compare these amounts to find out who saves the most.
To compare these amounts, we can write them in terms of a common denominator:
Amy: 0.2S
John: (3/5)S = (0.6)S
Emily: (5/13)S = (0.3846)S (approx.)
Therefore, we see that John saves the most of his salary each month, followed by Amy and then Emily.
Working out:
Let's assume that each person earns $1000 per month.
Amy:
Amount saved = 20% of $1000 = $200
Amount spent = $800
John:
Amount spent = 2/5 of $1000 = $400
Amount saved = $1000 - $400 = $600
Emily:
Let's assume that Emily saves $5x and spends $8x of her monthly salary.
Then, we have:
Amount saved = $5x
Amount spent = $8x
We know that the ratio of the amount saved to the amount spent is 5:8, so we can write:
$5x / $8x = 5/8
Solving for x, we get:
x = 8/13
Substituting the value of x, we get:
Amount saved = $5 x (8/13) x $1000 = $384.62 (approx.)
Amount spent = $8 x (8/13) x $1000 = $615.38 (approx.)
Therefore, we see that John saves the most of his salary each month, followed by Amy and then Emily.
A teacher has 36 pencils and 63 erasers to give away to 9 students. If the teacher wants each student to receive the same number of pencils and the same number of erasers, how many of each will each student receive
Answers
Answer:
4 pencils and 7 erasers
Step-by-step explanation:
36÷9=4
63÷9=7
Answer:
4 pencils and 7 erasers
Step-by-step explanation:
Each student will get: 36:9=4 (pencils)
63:9=7 (erasers)
Write a sine function that has an amplitude of 3, a midline of 5 and a period of pie
Answers
The sine function is y = 5 sin (\(16\pi x\) ) + 3.
What is Sine function?The function y =\(sin x\) defines a sine wave as a geometric waveform that oscillates (moves up, down, or side to side) frequently.
It is an s-shaped, smooth wave that oscillates above and below zero, to put it another way.
In its most general form, the sine wave can be described using the function y=\(a sin (bx)\)
Given:
Amplitude = 3
midline= 5
As, we know
General sine function: a sin b\((x- c)\) + d
and, amplitude = absolute value of a
b = 2π / period
c = phase shift (horizontal shift)
d = vertical shift (i/e., midline is y = d)
So,
a = 5, d = 3, and b = 2π / (1/8) = 16π, c = 0
Substituting the above value in Sine function we get
Thus, y = 5 sin (\(16\pi x\)) + 3
Learn more about sine function here:
https://brainly.com/question/27716924
#SPJ1
Help me please ASAP!!!!:::;;

Answers
Answer:
4/5 or 0.8 in decimal form
Step-by-step explanation:
slope is rise/run
4/5 as it goes 4 up and 5 to the right