Solve the following initial-value problem over the interval from x=0 to 1. dy/ dx = (1 + 2x) Vy, y(0) = 1 1. (10 points) Solve it analytically. 2. (10 points) Use Euler's method with h=0.5 3. (10 points) Use Heun's method with h=0.5. Iterate the corrector to es = = 1 % 4. (10 points) Use the midpoint method with h=0.5.
Answers
The solution to the initial-value problem is:
ln|y| = x + x^2
y = e^(x+x^2)
The approximate solution using Euler's method with h=0.5 is y(1) ≈ 2.25.
The approximate solution using the midpoint method with h=0.5 is y(1) ≈ 2.4638671875.
The approximate solution using Heun's method with h=0.5 and es=1% is y(1) ≈ 2.203125.
1. Analytical Solution:
To solve the given initial-value problem, we can use the method of separating variables. We have:
dy/dx = (1 + 2x) * y
Separating the variables, we get:
dy/y = (1 + 2x) * dx
Integrating both sides, we get:
ln|y| = x + x^2 + C
where C is the constant of integration. Now, using the initial condition y(0) = 1, we get:
ln|1| = 0 + 0 + C
C = 0
2. Euler's Method:
Using Euler's method with h=0.5, we can approximate the solution to the initial-value problem. We have:
h = 0.5
x0 = 0, y0 = 1
xn = 1
n = (xn - x0)/h = (1-0)/0.5 = 2
Using the given differential equation, we can write:
y1 = y0 + h * dy/dx(x0, y0)
y1 = 1 + 0.5 * (1 + 2*0) * 1
y1 = 1.5
Similarly, we can calculate y2:
y2 = y1 + h * dy/dx(x1, y1)
y2 = 1.5 + 0.5 * (1 + 2*0.5) * 1.5
y2 = 2.25
3. Heun's Method:
Using Heun's method with h=0.5, we can improve the approximation obtained in part (2). We have:
h = 0.5
x0 = 0, y0 = 1
xn = 1
n = (xn - x0)/h = (1-0)/0.5 = 2
Using the given differential equation, we can write:
yi+1* = yi + (h/2) * [dy/dx(xi, yi) + dy/dx(xi+1, yi+1*)]
To apply this formula, we need to calculate yi+1* iteratively. Let's start with an initial guess:
y1* = y0 + h * dy/dx(x0, y0)
y1* = 1 + 0.5 * (1 + 2*0) * 1
y1* = 1.5
Now, we can calculate yi+1* using the formula:
y1+1* = y0 + h * dy/dx(x0, y0) + (h/2) * [dy/dx(x0, y0) + dy/dx(x1, y1*)]
y1+1* = 1 + 0.5 * (1 + 2*0) * 1 + (0.5/2) * [(1 + 2*0) * 1 + (1 + 2*0.5) * 1.5]
y1+1* = 1.875
Now, we can calculate y2* using the formula:
y2* = y1 + (h/2) * [dy/dx(x1, y1) + dy/dx(x2, y2*)]
y2* = 1.5 + 0.5 * (1 + 2*0.5) * 1.875
y2* = 2.203125
4. Midpoint Method:
Using the midpoint method with h=0.5, we can obtain another approximation to the solution. We have:
h = 0.5
x0 = 0, y0 = 1
xn = 1
n = (xn - x0)/h = (1-0)/0.5 = 2
Using the given differential equation, we can write:
yi+1 = yi + h * dy/dx(xi+1/2, yi+1/2)
To apply this formula, we need to calculate yi+1/2 iteratively. Let's start with an initial guess:
y1/2 = y0 + (h/2) * dy/dx(x0, y0)
y1/2 = 1 + 0.25 * (1 + 2*0) * 1
y1/2 = 1.125
Now, we can calculate yi+1 using the formula:
y1+1 = y0 + h * dy/dx(x1/2, y1/2)
y1+1 = 1 + 0.5 * (1 + 2*0.25) * 1.125
y1+1 = 1.796875
Similarly, we can calculate y2:
y2 = y1+1 + h * dy/dx(x3/2, y3/2)
y2 = 1.796875 + 0.5 * (1 + 2*0.75) * 1.953125
y2 = 2.4638671875
Know more about Euler's method here;
https://brainly.com/question/14309211
#SPJ11
Related Questions
Why Eulerian path can be implemented in linear time, but not Hamiltonian path?
Answers
Eulerian path can be implemented in linear time because it follows a specific rule: a connected graph can have an Eulerian path if and only if it has either zero or two vertices of odd degree.
This means that the algorithm can quickly determine whether or not a graph has an Eulerian path by simply counting the number of odd degree vertices. This can be done in linear time, making the implementation of Eulerian path efficient and fast.
On the other hand, Hamiltonian path does not follow a specific rule, and there is no known efficient algorithm to determine whether or not a graph has a Hamiltonian path.
This means that the implementation of Hamiltonian path requires checking all possible paths in the graph, which can take a long time and is not efficient. Therefore, Hamiltonian path cannot be implemented in linear time like Eulerian path can.
To know more about Eulerian path click on below link:
https://brainly.com/question/27979322#
#SPJ11
Pls answer the question correct

Answers
Answer: 40
Step-by-step explanation
if you look at the number 4 it says it = 10
Then you look at 6 and it = 15
then you look at 8 and it = 20
SO everytime you add 2 it goes up 5.
So if you take the 8 and add 2 that's 10 and 10=25
So when you make your way to 16 it would be 40.
Simplify the square root of 3/8

Answers
Have a great day :)
steve was offered $5,025 per year for a weekend lifeguarding job at a local pool he wants to know how much his monthly income will be at this salary level what is his rate of pay in dollars per month
Answers
Answer:
418.75
Step-by-step explanation:
5025/12 (12 months in one year)
418.75 or almost 420 dollars a month
to check the answer:
418.75*12
5025
If h(x) = f(x) - g(x) = 2x, at what x-value will f(x) = g(x) + 20?
a) x = 20
b) x = 10
c) x = 5
d) x = 2
Answers
Answer:
B
Step-by-step explanation:
This is a neat question
f(x) - g(x) = 2x Add g(x) to both sides
f(x) = g(x) + 2x
Now you need the right hand side to have 20 added to g(x).
2x must = 20
2x = 20 Divide by 2
x = 20/2
x = 10
So the answer must be x = 10
(a) Are the axis and angle always uniquely defined for a rotation? If not, explain the conditions under
which the axis and angle are not uniquely defined.
(b) Write the axis-angle representation and the quaternion corresponding to the rotation matrix.
Answers
The axis and angle always uniquely defined for a rotation As we know that, From the Euler's rotation theorem
What is Angle?
An angle is a figure created by two rays, known as the angles' sides, that share a common terminus, known as the angle's vertex. Angles formed by two rays are located in the plane containing the rays. Angles are also generated when two planes intersect. These are known as dihedral angles.
a) As we know that, From the Euler's rotation theorem, we know that any rotation can be expressed as a single rotation about some axis. The axis is the unit vector (unique except for sign) which remains unchanged by the rotation. The magnitude of the angle is also unique, with its sign being determined by the sign of the rotation axis.
b)
\(\sqrt{3/2}x^{2} +1/2(\sqrt{3-1}x^{2} =x^{2} \\\\\sqrt{3/2}x^{2} +\sqrt{3/2} x^{2} - 1/2x^{2} =x^{2}\)
now using x = 0 will get xcube =0 but x cos x square one should be non zero because eigen vector always non zero so take aribatary
A rotation's axis and angle are always uniquely determined. As we know from Euler's rotation theorem,
To learn more about Angle visit:
brainly.com/question/14569348
#SPJ4
how do i right it please help

Answers
The contrapositive statement is:
If x ≠ 2, then x^2 ≠ 4
And it is false.
How to write the contrapositive statement?
First, we have two propositions:
p = "x^2 = 4"
q = "x = 2"
The contrapositive statement is:
¬q → ¬p
The negation of the propositions are:
¬q = "x ≠ 2"
¬p = "x^2 ≠ 4"
Then the contrapositive statement with the given propositions is:
If x ≠ 2, then x^2 ≠ 4
Now, is this statement true?
No, because we can have:
x = -2 (which is different than 2, so the hypothesis is true)
and x^2 = (-2)^2 = 4
Then the conclusion is false, so the statement is false.
If you want to learn more about conditional statements:
https://brainly.com/question/11073037
#SPJ1
Kathryn's school is selling tickets to a spring musical. On the first day of ticket sales the school
sold 4 adult tickets and 3 student tickets for a total of $73. The school took in $232 on the
second day by selling 13 adult tickets and 9 student tickets. Find the price of an adult ticket and
the price of a student ticket.
A) adult ticket: $13, student ticket: $7
C) adult ticket: $19, student ticket: $10
O A
OB
O C
O D
B) adult ticket: $10, student ticket: S9
D) adult ticket: $7, student ticket: $13
Answers
Answer:
A
Step-by-step explanation:
$13 × 4 = $52
$7 × 3 = $21
= $52 + $21= $73
$13 × 13 = $169
$7 × 9 = $63
= $169 + $63
=$232
HELP QUICK PLSS
The shadow of the tree is 40 feet long. A yard-stick placed next to the tree casts a 6 foot shadow. How tall is the tree?
Answers
Answer:
pretty sure the tree's 20 feet
According to proportion if a tree casts a shadow of 40 feet it;s height is 20 feet.
What are ratio and proportion?A ratio is a comparison between two similar quantities in simplest form.
Proportions are of two types one is the direct proportion in which if one quantity is increased by a constant k the other quantity will also be increased by the same constant k and vice versa.
In the case of inverse proportion if one quantity is increased by a constant k the quantity will decrease by the same constant k and vice versa.
We know 1 yard is 3 feet.
Given, The shadow of the tree is 40 feet long. A yardstick placed next to the tree casts a 6-foot shadow and assuming the height of the tree to be x.
∴ x : 40 : : 3 : 6.
x/40 = 3/6.
6x = 120.
x = 20 feet.
learn more about proportion here :
https://brainly.com/question/7096655
#SPJ2
Lashawn used 44 stamps to mail a package. He used a
combination of $0.50 stamps, $0.35 stamps, $0.02 stamps,
totaling $15.01. If the number of $0.35 stamps is nine less
than twice the number of $0.50 stamps, find the number of
each type of stamp.
Answers
Answer:
Lashawn used 15, $0.50 stamps, 21, $0.35 stamps, and 8, $0.02 stamps to mail the package
Step-by-step explanation:
The given parameters are;
The number of stamps Lashawn used to mail the small package = 44
The price of the combination of 44 stamp = $15.01
The price categories of the stamps are $0.50, $0.35, and $0.02
The number of $0.35 stamps = 2 × The number of $0.50 stamps - 9
Let, x represent the number of $0.50 stamps Lashawn used to mail the package
We have;
The number of $0.50 stamps Lashawn used to mail the package = x
The number of $0.35 stamps = 2 × x - 9 = 2·x - 9
The number of $0.35 stamps = 2·x - 9
The number of $0.02 stamps = 44 - x - (2·x - 9) = 44 - x - 2·x + 9 = 53 - 3·x
The number of $0.02 stamps = 53 - 3·x
Which gives;
0.5 × x + 0.35 × (2·x - 9) + 0.02 × (53 - 3·x) = 15.01
0.5·x + 0.7·x - 3.15 + 1.06 - 0.06·x = 15.01
1.14·x - 2.09 = 15.01
1.14·x = 15.01 + 2.09 = 17.1
x = 17.1/1.14 = 15
x = 15
The number of $0.50 stamps Lashawn used to mail the package = x = 15 stamps
The number of $0.50 stamps Lashawn used = 15 stamps
The number of $0.35 stamps Lashawn used = 2·x - 9 = 2 × 15 - 9 = 21 stamps
The number of $0.02 stamps Lashawn used = 53 - 3·x = 53 - 3 × 15 = 8 stamps.
an open box is to be made from a two-foot by three-foot rectangular piece of metal by cutting equal squares from the corners and turning up the sides. find the volume of the largest box that can be made in this manner. round your final answer to the nearest hundredth.
Answers
The volume for the largest box will be 1.056 foot³. This can find out by application of differentiation.
What is AOD?
AOD is nothing but application of differentiation. It implies scopes where we can use differentiation to make our calculations easy.
Here, given
Length and breadth = 2,3 foot
Let us consider length of side of square = x
So, after cutting squares left sides of rectangular sheet = 2-2x , 3-2x
So, volume = (2-2x)*(3-2x)*x
v = 4x³ - 10x² + 6x
To find largest volume , \(\frac{dv}{dx}\) = 0
\(\frac{dv}{dx}\) = 12x² - 20x + 6
12x² - 20x + 6 = 0
x = 0.4 , 1.3
But, for 1.3 volume will be negative i.e. not possible.
So, volume = 2.2*1.2*0.4
= 1.056 foot³
Learn more about differentiation from given link:
https://brainly.com/question/954654
#SPJ4
Find the value of x from the following. X/4 = 6
x/2 = 12. 5
Answers
Answer:
x = 24; x = 25
Step-by-step explanation:
Question 1
x/4 = 6
x = 24 *multiply both sides by the denominator to isolate the x value
Question 2
x/2 = 12.5
x = 25 *multiply both sides by the denominator to isolate x
Could someone help me, please



Answers
Answer:
Q1: No solutions
Q2: x=2, y=-2
Q3: x=1, y=4
Step-by-step explanation:
Q1: Found out 0y = 18 which is impossible therefore no solution.
Q2:
In the first equation: \(2x - 4y = 12\)
Let's express x in terms of y by changing the subject. Follow my steps.
\(2x = 12+4y\)
\(x = \frac{12+4y}{2}\)
Now let's put the x above into the second equation: \(-14x-4y=-20\)
It becomes: \(-14(\frac{12+4y}{2})-4y=-20\). Follow my steps.
\(-7(12+4y)=-20+4y\)
\(-84-28y=-20+4y\)
\(-32y=64\)
\(y=-2\)
Put y = -2 into the first equation:
\(2x-4(-2)=12\)
\(2x+8=12\)
\(2x=12-8\)
\(2x=4\)
\(x=2\)
Q3:
Multiply the first equation by 3 and the second equation by 7, so that both are 21x.
1st equation:
\(3(7x-3y)=3(-5)\)
\(21x-9y=-15\)
2nd equation:
\(7(3x+2y) = 7(11)\)
\(21x+14y = 77\)
We can now substract the 2nd equation with the 1st equation so that both 21x cancels out and only the variable y remains.
\(21x-9y-(21x+14y)=-15-77\)
\(21x-9y-21x-14y=-92\)
\(-23y=-92\)
\(y=4\)
Put y = 4 into the second equation to find x.
\(3x+2(4)=11\)
\(3x+8=11\)
\(3x=11-8\)
\(3x = 3\)
\(x=1\)
A car travels 420 miles on 15 gallons of gas. Express this as a unit rate. (How far does it travel on one gallon of gas?)
Answers
Answer:28
Step-by-step explanation: divide 420 by 15
Please Help
Can someone explain where the 4i to the square root of 3 came from?

Answers
Answer:
see explanation
Step-by-step explanation:
note that \(\sqrt{-1}\) = i
\(\sqrt{64-112}\)
= \(\sqrt{-48}\)
= \(\sqrt{16(3)(-1)}\)
= \(\sqrt{16}\) × \(\sqrt{3}\) × \(\sqrt{-1}\)
= 4 × \(\sqrt{3}\) × i
= 4i\(\sqrt{3}\)
A cube has a side length x and an each dimension is being increased by y, guys. :)
A). Write an expression for the surface area of the new cube, and then expand, and simplify, guys. :)
B). Please find the difference of the surface areas of the new cube and the original cube, guys. :)
Answers
Surface area of old cube
6(side)²6x²Side of new cube
x+ySurface area
6(x+y)²6(x²+y²+2xy)6x²+6y²+12xyDifference
6y²+12xyAnswer:
A) 6(x + y)² = 6x² + 12xy +6y²
B) 12xy +6y²
Step-by-step explanation:
Surface area of a cube = 6s² (where s is the side length)
Part A
Given:
x = side length of original cube⇒ Surface area of the original cube = 6x²
If the side length of the cube is increased by y, then:
(x + y) = side length of new cube⇒ Surface area of the new cube = 6(x + y)²
Expand and simplify:
⇒ 6(x + y)²
⇒ 6(x + y)(x + y)
⇒ 6(x² + xy + xy + y²)
⇒ 6x² + 12xy +6y²
Part B
To find the difference between the surface areas of the new and original cubes, subtract the surface area of the original cube from the surface area of the new cube:
⇒ SA of new cube - SA of original cube
⇒ 6x² + 12xy +6y² - 6x²
⇒ 12xy +6y²
5x-3y=30
7x-3y=36
elimantion method
Answers
Answer:
x = 3 and y = -5
Step-by-step explanation:
\(5x - 3y = 30 \\ 7x - 3y = 36 \\ \\ - 1(5x - 3y = 30) \\ 7x - 3y = 3 \\ \\ - 5x + 3y = - 30 \\ 7x - 3y = 36 \\ 2x = 6 \\ x = 3 \\ \\ 5(3) - 3y = 30 \\ 15 - 3y = 30 \\ - 3y = 30 - 15 \\ - 3y = 15 \\ \frac{ - 3y}{ - 3} = \frac{15}{ - 3} \\ y = - 5\)
Carlos has a box full of 48 brown, 3 yellow, and 2 orange toy blocks. Determine how likely it is for Carlos to randomly select each color toy block from the box. Select Unlikely, Neither Likely nor Unlikely, or Likely for each color toy block.
Answers
Answer:
likely nor unlikely
Step-by-step explanation:
carlos can pivk any
It is likely for Carlos to randomly select a brown block, but unlikely for him to randomly select a yellow or orange block.
What are permutation and combination?A permutation is an orderly arrangement of things or numbers. Combinations are a means to choose items or numbers from a collection or set of items without worrying about the items' chronological order.
For each color, we can determine the probability of selecting that color by dividing the number of blocks of that color by the total number of blocks in the box:
Brown: 48 blocks out of 53 total blocks = 48/53
≈ 0.91, which is Likely.
Yellow: 3 blocks out of 53 total blocks = 3/53
≈ 0.06, which is Unlikely.
Orange: 2 blocks out of 53 total blocks = 2/53
≈ 0.04, which is Unlikely.
Therefore, it is likely for Carlos to randomly select a brown block, but unlikely for him to randomly select a yellow or orange block.
Learn more about Permutation and combination here:
https://brainly.com/question/15268220
#SPJ3
What is the inequality shown?

Answers
Answer:
-4<n≤5
If you are using another variable just replace it in.
The information in the number line is an interval (-4,5]
What is Interval Notation?Interval Notation is a way of expressing a subset of real numbers by the numbers that bound them. We can use this notation to represent inequalities. We know an interval expressed as 1 < x < 5 denotes a set of numbers lying between 1 and 5 and it is represented as (1,5)
Given here, the line extends to -4 and ends at 5 but the it is open on the LHS and closed on the RHS and thus the interval notation is (-4,5]
Hence the interval represented in the number line is (-4,5]
Learn more about interval notation here:
https://brainly.com/question/14264237
#SPJ2
A hospital's investigation committee randomly surveyed 70 patients who had waited in the emergency department. The committee found a mean of 1.5 hours and a sample standard deviation of 0.5 hours. Answer the following questions to help construct a 96% confidence interval: 1. Should the z or the t distribution be used for this problem? Why? Then, find the critical value of the appropriate distribution for a 96% level of confidence. Provide evidence of your reasoning and give your final answer rounded to exactly three decimal places. 2. Use any method to construct an appropriate confidence interval. Provide evidence of your reasoning, and your final answer should be in inequality notation. where each limit is rounded to exactly 2 decimal places. 3. (to be done later) A different hospital heard about these results and wants to know how many people to survey to be 95% confident that they will estimate the wait to within three minutes. Determine the appropriate minimum sumple size, and provide evidence of your reasoning
Answers
1) In this problem, the t-distribution should be used since the sample size is less than 30. The critical value of the t-distribution with 69 degrees of freedom (n - 1) for a 96% level of confidence is 1.994. The reasoning behind using the t-distribution is that the sample size is less than 30 and hence the population standard deviation is unknown.
2) For constructing a 96% confidence interval for the mean waiting time, use the following formula:- \[CI= \left[ \overline{x}-t_{0.02/2} \times \frac{s}{\sqrt{n}},\text{ }\overline{x}+t_{0.02/2} \times \frac{s}{\sqrt{n}} \right]\]
Where, \[\overline{x}\] = 1.5, sample mean; s = 0.5, sample standard deviation; n = 70, sample size; t0.02/2 is the critical value of the t-distribution at a significance level of 0.04/2 = 0.02,
which corresponds to a 96% level of confidence. Using a t-distribution with 69 degrees of freedom (n - 1), the critical value for t0.02/2 is 1.994, as computed earlier.
Plugging these values in the formula we get:\[CI= \left[ 1.37,1.63 \right]\]Thus, the 96% confidence interval for the mean waiting time is \[1.37 \leq \mu \leq 1.63.\]3)
To determine the minimum sample size, we need to find the margin of error, which is 3 minutes. The margin of error can be given by:
\[ME = z_{\alpha/2} \times \frac{s}{\sqrt{n}}\]
To know more about distribution visit:
https://brainly.com/question/29664127
#SPJ11
6. How many times larger is the first number in the pair than the second? a. 34 is times larger than 3³. times larger than 5². times larger than 78. times larger than 17. times larger than 5*. b. 5³ is_____ c. 710 is d. 176 is e. 5 1⁰ is

Answers
3⁴ is 3 times larger than 3³, 5³ is 5 times larger than 5², 7¹⁰ is 49 times larger than 7⁸ and 17⁶ is 289 times larger than 17⁴.
3⁴ / 3³ = (3 × 3 × 3 × 3) / (3 × 3 × 3) = 3
This means that 3⁴ is 3 times larger than 3³.
5³ is 5 times larger than 5².
5³ / 5² = (5 × 5 × 5) / (5× 5) = 5
7¹⁰ is 49 times larger than 7⁸.
7¹⁰/ 7⁸ = 7² =49
17⁶ is 289 times larger than 17⁴.
17⁶ /17⁴ = 289
Hence, 3⁴ is 3 times larger than 3³, 5³ is 5 times larger than 5², 7¹⁰ is 49 times larger than 7⁸ and 17⁶ is 289 times larger than 17⁴.
To learn more on Number system click:
https://brainly.com/question/22046046
#SPJ1
Pamela is 9 years younger than Jiri. The sum of their ages is 67. What is Jiri's age?
Answers
Answer:
Jiri is 38 years old.
Step-by-step explanation:
First, 67 - 29 = 38 and 29 + 9 = 38.
Hope this helps!
What is printed by print(1+3/2*2)
Answers
The output of print(1+3/2*2) is 5.0
This is because the order of operations in arithmetic dictates that multiplication and division should be performed before addition and subtraction.
So, first 3/2 is evaluated which gives 1.5, then 1.5 is multiplied by 2 to give 3, and finally, 1 is added to 3 to get the result of 5.0. Hence, 5.0 will be printed by the print (1+3/2*2).
Note that the result is a floating-point number because division between two integers in Python 3. x always results in a float, even if the result is a whole number.
To learn more about print, click here:
https://brainly.com/question/27646993
#SPJ11
e=mc^2 solve for c please help will mark brainliest
Answers
Answer:
c= - (sqr em)/m
Step-by-step explanation:
Answer:
c = ± \(\sqrt{\frac{e}{m} }\)
Step-by-step explanation:
Given
e = mc² ( divide both sides by m to isolate c² )
\(\frac{e}{m}\) = c² ( take the square root of both sides )
c = ± \(\sqrt{\frac{e}{m} }\)
PLEASE HELP ME ILL GIVE BRAINLIEST IF ITS RIGHT
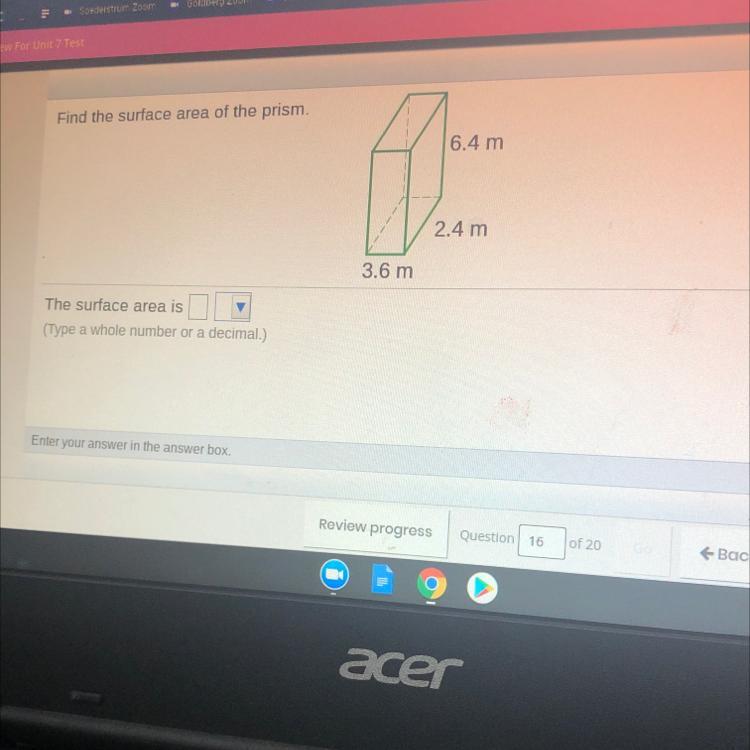
Answers
Answer:
94.08m
Step-by-step explanation:
Just multiplly each sides dimensions for all 6 sides.
PLS IM BEGGING ILL GIVE CROWN!
ANSWER PLSSS FOR MY FINALS! A soccer team sells T-shirts for a fundraiser. The company that makes the T-shirts charges $\$10$ per shirt plus a $\$20$ shipping fee per order.
a. Write and graph an equation that represents the total cost (in dollars) of ordering the shirts. Let $t$ represent the number of T-shirts and let $c$ represent the total cost (in dollars).
Equation: c (x) = 10x + 20
PLS MAKE THE GRAPH TOO
HAPPY SUMMMER
Answers
The graph is a straight line that starts at the point (0, 20) and increases by 10 units on the y-axis for every 1 unit increase on the x-axis. This represents the linear relationship between the number of T-shirts ordered and the Total cost.
The total cost of ordering the shirts:
\[c(x) = 10x + 20\]
In this equation, $x$ represents the number of T-shirts ordered, and $c(x)$ represents the total cost in dollars. The cost per shirt is $10, and there is a flat shipping fee of $20 per order.
To graph this equation, we can plot points on a coordinate plane, where the x-axis represents the number of T-shirts ($x$) and the y-axis represents the total cost ($c$) in dollars. We can choose a few values for $x$ and calculate the corresponding values of $c$ using the equation.
Let's choose some values of $x$ and calculate the corresponding values of $c$:
- If $x = 0$, there are no T-shirts ordered, so the total cost is $c(0) = 10(0) + 20 = 20$.
- If $x = 1$, there is one T-shirt ordered, so the total cost is $c(1) = 10(1) + 20 = 30$.
- If $x = 2$, there are two T-shirts ordered, so the total cost is $c(2) = 10(2) + 20 = 40$.
We can plot these points on the graph and connect them to create a straight line. Here's how the graph looks:
|
50 +-----------------------------------------------------------
|
40 + * (2, 40)
|
30 + * (1, 30)
|
20 + * (0, 20)
|
+-----------------------------------------------------------
0 1 2
The graph is a straight line that starts at the point (0, 20) and increases by 10 units on the y-axis for every 1 unit increase on the x-axis. This represents the linear relationship between the number of T-shirts ordered and the total cost.
For more questions on total cost
https://brainly.com/question/843074
#SPJ8
Look at the steps used when solving 3(x - 2) = 3 for X.
3(x - 2) = 3
3x - 6 = 3
3x - 6 + 6 = 3 + 6
3x = 9
Write the original equation.
Use the Distributive Property.
Step 1
Step 2
3x 9
3
3 3
Step 3
x = 3
Step 4
Which step is the result of combining like terms?
Which step is justified by division property of equality?
Answer in at least TWO COMPLETE SENTENCES.
Answers
Answer:
3×-6=3
3×=3+6
3×=9
×=3
Step-by-step explanation:
multiply 3 by the variables in the bracket.
then you will get 3×-6=3.
take the -6 to the right hand side and it becomes+6
then you get 3×=3+6 therefore =3×=9
then divide both sides by 3.
3×÷3 and 9÷3
×=3
a poster is 16 feet. It is 3 feet wide. How tall is it?
Answers
Answer:
13 feet tall
Step-by-step explanation:
Poster = 16 feet
width of poster = to 3 feet
16 - 3 = 13
Poster Height : 13 feet
Answer:
13 feet
Step-by-step explanation:
16 is the length and width combined, so you just subtract the width (3) from 16 to get the length (13)
a box is 60 cm long. which of these is closest to the length of this box in feet?
1 inch = 2.54 cm
a. 1.84 feet
b. 1.97
c. 2.54
d. 2.82
Answers
Answer:
b. 1.97
Step-by-step explanation:
1cm≈0.032feet
60/0.032≈1.97feet
Nationwide, it is estimated that 40% of service stations have gas tanks that leak to some extent. A new program in California is designed to lessen the prevalence of these leaks. We want to assess the effectiveness of the program by seeing if the percentage of service stations whose tanks leak has decreased. To do this, we randomly sample 27 service stations in California and determine whether there is any evidence of leakage. In our sample, only 7 of the stations exhibit any leakage. Is there evidence that the new program is effective
Answers
Answer:
Since the calculated value of z= -1.496 does not fall in the critical region z < -1.645 we conclude that the new program is effective. We fail to reject the null hypothesis .
Step-by-step explanation:
The sample proportion is p2= 7/27= 0.259
and q2= 0.74
The sample size = n= 27
The population proportion = p1= 0.4
q1= 0.6
We formulate the null and alternate hypotheses that the new program is effective
H0: p2> p1 vs Ha: p2 ≤ p1
The test statistic is
z= p2- p1/√ p1q1/n
z= 0.259-0.4/ √0.4*0.6/27
z= -0.141/0.09428
z= -1.496
The significance level ∝ is 0.05
The critical region for one tailed test is z ≤ ± 1.645
Since the calculated value of z= -1.496 does not fall in the critical region z < -1.645 we conclude that the new program is effective. We fail to reject the null hypothesis .